Ce document traite de l'étude de la résistance au flambement des poteaux en se fondant sur l'Eurocode 2. Il aborde les méthodes de vérification de la stabilité des poteaux, tant à froid qu'à chaud, ainsi que les implications en cas d'incendie. L'étude inclut des applications pratiques pour le dimensionnement des poteaux de section circulaire et la vérification de la stabilité au feu.

1. École des Ponts ParisTech
Département de Génie Civil et Construction
Projet de Fin d’Études
Étude de la résistance au flambement des
poteaux à froid et à chaud suivant l'EC2
Tuteur Entreprise : Mme Évelyne
OSMANI
Tuteur École : M. Emmanuel
BOUCHON
Projet réalisé au sein du B.E.S Eiffage Construction
Van Thuan PHAM - Département de
GCC
03 sept 2014 1

2. INTRODUCTION
 Contexte
De nombreux projets de BTP ont adopté l’Eurocode comme la norme de construction.
Cette nouvelle norme substitue, par la voie contractuelle, le BAEL 91 et d’autres textes
règlementaires (DTU). Il nécessite pour les ingénieurs de bureau d’études d’étudier
cette nouvelle norme et d’appliquer dans leurs projets.
 Problématique
L’EC2 propose 3 méthodes de justification de la stabilité des poteaux et des voiles.
 En quoi consiste le dimensionnement et la vérification de stabilité des poteaux
tenant compte de l’effet du second ordre proposés par les normes Eurocodes ?
 Comment s’évolue le comportement du matériau à froid et à chaud suivant l’EC2?
 Par quelle mesure pouvons-nous vérifier la stabilité en cas d’incendie ?
Van Thuan PHAM - Département de
GCC
03 sept 2014 2

3. PLAN DE L’EXPOSÉ
1. État limite ultime de résistance
2. État limite ultime de stabilité de forme
(flambement)
3. Application au dimensionnement des poteaux de
section circulaire
4. Vérification de la stabilité au feu selon l’EC2
5. Conclusion
Van Thuan PHAM - Département de
GCC
03 sept 2014 3

4. 1. État limite ultime de résistance
 Matériaux
Béton : Classe C12/15 – C90/105
  
      
 2
  2


  
2 2
1 (1 ) pour 0
pour
c n
cd c c
c c
cd c c cu
f
f

 
 
  
2 1
avec 1.05 /
1
1
1 ( 2)
0
c
c
c cd cm c cd
c cu
k
f k E f
k



 
 

 

 
 
  
    


a) Loi parabole - rectangle b) Lo i Sargin
Paramètres C40/50
fck (MPa) 40
fcm (MPa) 48
fctm (MPa) 3,5
fctk,0,05 (MPa) 2,5
Ecm (GPa) 35
εc1 (‰) 2,3
εcu1 (‰) 3,5
εc2 (‰) 2
εcu2 (‰) 3,5
n 2
εc3(‰) 1,75
εcu3 (‰) 3,5
Van Thuan PHAM - Département de
GCC
03 sept 2014 4

5. 1. État limite ultime de résistance
 Matériaux
Aciers : Barres HA, Es=2.10+5MPa, fyk = 500MPa
Acier HA εuk εud k
Classe A 25 ‰ 22,5 ‰ 1,05
Classe B 50 ‰ 45 ‰ 1,08
Classe C 75 ‰ 67,5 ‰ 1,15
Dnom Asi (cm²)
HA05 0,20
HA06 0,28
HA08 0,50
HA10 0,79
HA12 1,13
HA14 1,54
HA16 2,01
HA20 3,14
HA25 4,91
HA32 8,04
HA40 12,57
Classe de
ductilité de l’acier
Van Thuan PHAM - Département de
GCC
03 sept 2014 5

6. 1. État limite ultime de résistance
 Règle de trois pivots
Van Thuan PHAM - Département de
GCC
03 sept 2014 6

7. 1. État limite ultime de résistance
 Diagramme d’interaction (ELU).
Le diagramme d’interaction
détermine la frontière du domaine
de résistance d’un poteau.
Van Thuan PHAM - Département de
GCC
03 sept 2014 7

8. 2. État limite de stabilité de forme
 Force critique d’Euler
d y x M x N y x
1 ( ) ( ) . ( )
( )
 
on pose: ( ) cos sin
      
Avec y(0)=0 et y( )=0; on obtient :

²
2
0
   
B
EI
N
l

Hypothèse:
- Colonne bi-articulée
- Charge axiale centrée
- Matériau homogène,
isotrope
- Comportement
élastique
(EI constante)
- Déformée sinusoïdale
2
2
r x dx EI EI
2
( )
2
( ) 0
d y x N
y x
dx EI
2
1 2
0
N
y x C x C x
EI
2

0
( ) sin
k
y x C x
l

Van Thuan PHAM - Département de
GCC
03 sept 2014 8

9. 2. État limite de stabilité de forme
 Amplification du moment
N est une force axiale excentrée (imperfections géométriques) avec l’excentricité y0
varie selon une loi sinusoïdale :

0 0
( ) ( ).
0
cr B
B
B
N N
N
M x Ny x
N N



Le moment fléchissant s’exprime par :
En résolvant l’équation différentielle, on obtient:
0
( ) sin
x
y x e
l

Mx  Ny y0 
coefficient
d’amplificatio
n
Van Thuan PHAM - Département de
GCC
03 sept 2014 9

10. 2. État limite de stabilité de forme
 Méthode de la rigidité
Principe : Majoration du moment au 1er ordre.
On évalue la rigidité nominale :
Avec :
D’ou:
EI  Kc .Ecd .Ic  Ks .Es .Is
N
1 2 1 2 . / (1 ) ; / 20 ; (0,2; )

 
0 (1 )
/ 1 Ed Ed
B Ed
 
 
l c
M M
N N

EI
2
0 0
N
0
² ²
; =
B
c = {8; 9,6; 10; 12}
170
Ed
c eff ck
c cd
K k k k f k Min
A f

   
1 s K 
Van Thuan PHAM - Département de
GCC
03 sept 2014 10

11. 2. État limite de stabilité de forme
 Méthode de la courbure
On évalue la courbure nominale de la section critique:
Avec:
1 1
. . r K K
r r  
0
1
0

yd yd
 
0, 45. .0, 45.
s
f
r d E d
Van Thuan PHAM - Département de
GCC
03 sept 2014 11

12. 2. État limite de stabilité de forme
 Méthode de la courbure (suite)
K Max f
 (1 ; 1  (0,35  / 200 -  /150). 
)  ck eff
N 
N
ud Ed
r
ud bal
K
N N


2
0
 
1
1
e e ; avec c={8 ; 10}
c r
On obtient :
. Ed Ed M  N e
Van Thuan PHAM - Département de
GCC
03 sept 2014 12

13. 2. État limite de stabilité de forme
 Méthode générale
(méthode de Faessel, méthode de l’équilibre)
Domaine d’application:
o Poteaux élancés (élancement λ = ℓ0/i ≥ 60 ), chargés de façon excentrées.
o Poteaux de section constante, soumis à un effort normal constant.
o Poteaux articulés à leurs deux extrémités ou en console
o M0Ed de signe constant, section critique se situant à ℓ0/2 du sommet
Van Thuan PHAM - Département de
GCC
03 sept 2014 13
Hypothèse complémentaire:
• Béton: Loi de comportement type Sargin.
On tient compte du fluage en affinant
parallèlement à l’axe εc, de rapport (1+φeff).

14. 2. État limite de stabilité de forme
 Méthode générale
Excentricité externe :
l
1
. ext
e e e e
Excentricité interne :
Pour chaque courbure 1/r, on détermine εch
pour que : Nint = NEd.
Il en résulte :
2
0
1 2 1 2
 r
   
int
int
M
int
e
N

Van Thuan PHAM - Département de
GCC
03 sept 2014 14

15. 3. Application au dimensionnement des
poteaux de section circulaire
 Abaque d’interaction pour le calcul du ferraillage
théorique.
X
X
X
X
X
X
X
X
X
X
X
NEd
MRd(ρs)
MEd(ρs)
(courbure vs rigidité)
ρs ϵ [ρmin; ρmax])
Van Thuan PHAM - Département de
GCC
03 sept 2014 15

16. 3. Application au dimensionnement des
poteaux de section circulaire
 Détermination du ferraillage nécessaire.
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
Évolution de moments MRd et MEd (Rig vs Cb)
en fonction de ρs ϵ [ρmin; ρmax]
ρs,nécessaire
ρ (Rigidité) s,nécessaire
(Courbure)
0 0.005 0.01 0.015 0.02 0.025 0.03 0.035 0.04 0.045
Moment (MN.m)
ρs
MRd MEd(ρs) (Rig) MEd(ρs) (Cb)
Van Thuan PHAM - Département de
GCC
03 sept 2014 16

17. 3. Application au dimensionnement des
poteaux de section circulaire
 Détermination du ferraillage nécessaire (cas où on
prend ρs =ρmin)
1.2
1
0.8
0.6
0.4
0.2
0
ρs,nécessaire
(Rigidité)
0 0.005 0.01 0.015 0.02 0.025 0.03 0.035 0.04 0.045
Moment (MN.m)
ρs
MRd MEd(ρs) (Rig) MEd(ρs) (Cb)
ρs,min
(Courbure)
Van Thuan PHAM - Département de
GCC
03 sept 2014 17

18. 3. Application au dimensionnement des
poteaux de section circulaire
 Détermination du ferraillage nécessaire (cas où on
prend ρs =ρmax)
2.5
2
1.5
1
0.5
0
0 0.005 0.01 0.015 0.02 0.025 0.03 0.035 0.04 0.045
Moment (MN.m)
ρs
MRd MEd(ρs) (Rig) MEd(ρs) (Cb)
ρs,max
(Rigidité)
ρs,max
(Courbure)
Van Thuan PHAM - Département de
GCC
03 sept 2014 18

19. 3. Application au dimensionnement des
poteaux de section circulaire
 Disposition des armatures pratiques.
Van Thuan PHAM - Département de
GCC
03 sept 2014 19

20. 3. Application au dimensionnement des
poteaux de section circulaire
 Vérification de la section critique (par les trois
méthode).
Van Thuan PHAM - Département de
GCC
03 sept 2014 20

21. 3. Application au dimensionnement des
poteaux de section circulaire
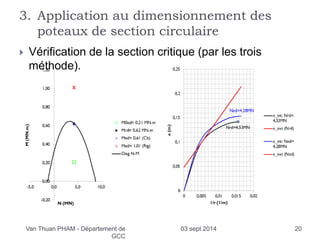
 Comparaison des trois méthodes
On détermine l’effort normal de résistance par les méthodes de la rigidité et de la
courbure en faisant varier l’effort N ϵ [0; Nult] ; Nult = Acfcd + Asfyd et en cherchant
l’intersection entre diagramme M-N et la courbe de moment fléchissant majoré au
second ordre.
Van Thuan PHAM - Département de
GCC
03 sept 2014 21
x
x

22. 3. Application au dimensionnement des
poteaux de section circulaire
 Comparaison des trois méthodes
ρs = 0,2% ρs = 2,0% ρs = 4,0%
Van Thuan PHAM - Département de
GCC
03 sept 2014 22

23. 4. Vérification de la stabilité au feu selon
EC2
L’Eurocode 1 et 2, partie 1-2 donne l’ensemble de règles applicables à la vérification
de la stabilité au feu des structures de bâtiment en béton armé (dalle, poutre, poteau,
…).
Méthodes :
 Méthodes des valeurs tabulées
 Méthodes de calcul simplifiées : isotherme à 500°C, méthode par tranches.
 Méthodes de calcul avancées
Van Thuan PHAM - Département de
GCC
03 sept 2014 23

24. 4. Vérification de la stabilité au feu selon
EC2
Actions du feu :
Courbe température/temps normalisée :
Coefficient de matériaux : 1 ; 1,2
 
 
s c
Coefficient de pondération des charges :
Van Thuan PHAM - Département de
GCC
G 

Q
k fi k
G Q
 

G k Q k


N N M M
 
 ;

Ed f i fi Ed Ed f i fi Ed
03 sept 2014 24
10 20 345 log (8 1) g     t 
Résistance au feu normalisé : R 30 ; R 60 ; … ; R240 (classe de résistance mécanique
pendant 30 ; 60 ; … ; 240 minutes d’exposition au feu normalisé.
Combinaison ELU accidentelles:
,1
,1 ,1
fi
, ,

25. 4. Vérification de la stabilité au feu selon
EC2
 Trois méthodes des valeurs tabulées
Objectif : Basée sur des essais expérimentaux au feu, les tableaux préétablis donnent
des dimensions minimales requises des éléments de structures en situation d’incendie.
 Section circulaire : diamètre minimum (Dmin) et enrobage requis (amin).
Exemple : Tableau de méthode B (interpolation linéaire entre valeurs admise)
Van Thuan PHAM - Département de
GCC
03 sept 2014 25

26. 4. Vérification de la stabilité au feu selon
EC2
 Distribution de températures dans la section et
courbes d’isotherme.
Équation de la chaleur (Fourrier)
2
   
 
 t c  
r
2
Transformation de l'équation
en différences finies
Van Thuan PHAM - Département de
GCC
03 sept 2014 26

27. 4. Vérification de la stabilité au feu selon
EC2
 Comportement du matériau à chaud.
o La résistance à la
compression du béton est
réduite à chaud.
o Les limites de déformation
εc1(θ) et εcu1(θ) du béton sont
fonction de températures.
o La résistance de l’acier est
fortement influencée par la
température.
Van Thuan PHAM - Département de
GCC
03 sept 2014 27

28. 4. Vérification de la stabilité au feu selon
EC2
 Méthode de l’isotherme à 500°C
Principe :
i. On ne tient compte que de la section du béton dont la température est inférieure à
500°C. Cette section réduite conserve ses caractéristiques à froid.
ii. Les barres d’acier travaillent avec leur résistance réduite à chaud.
iii. On détermine le diagramme M-N à chaud.
iv. On calcule les sollicitations tenant compte de l’effet au second ordre par l’une des
deux méthodes rigidité et courbure modifiées.
Van Thuan PHAM - Département de
GCC
03 sept 2014 28

29. 4. Vérification de la stabilité au feu selon
EC2
 Méthodes de calcul avancées
Principe :
i. On tient compte du comportement exacte de matériau (béton & acier).
ii. On définit des règles de pivots en se basant sur le diagramme de déformation εc1 de
la section
iii. On calcule le diagramme M-N à chaud.
iv. On calcule les sollicitations par l’une des deux méthodes modifiées (rigidité vs
courbure)
Van Thuan PHAM - Département de
GCC
03 sept 2014 29

30. 5. Conclusion
 Trois méthode de vérification de la stabilité au flambement (rigidité,
courbure, générale) ont été étudiées pour le calcul du ferraillage et la
justifications des poteaux. Il permet aussi d’optimiser la quantité des
armatures à mettre en place.
 En situation d’incendie, on dispose trois méthodes des valeurs tabulées.
Elles sont complétée par des méthodes de calcul avancées.
 Le programme de calcul développé est destiné aux ingénieurs comme un
outil de dimensionnement des structures selon l’EC2
Van Thuan PHAM - Département de
GCC
03 sept 2014 30

31. MERCI POUR VOTRE ATTENTION !
Si vous avez des questions ?
Van Thuan PHAM - Département de
GCC
03 sept 2014 31