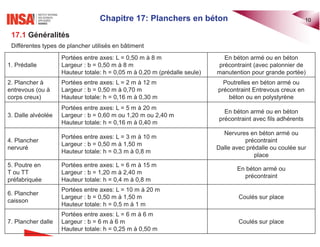
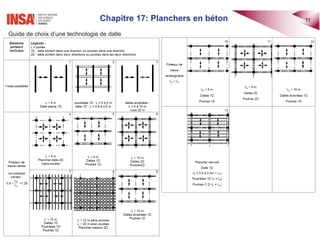
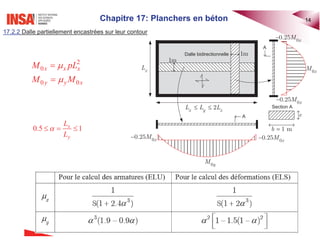
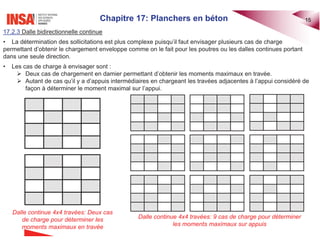
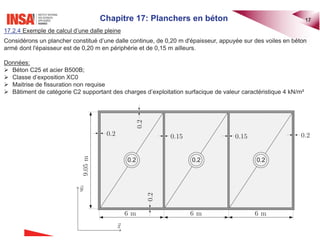
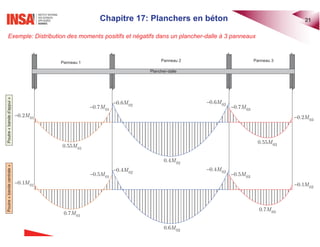
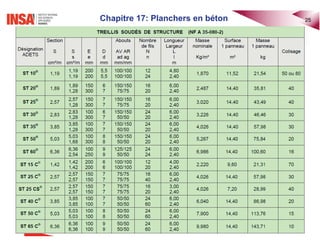
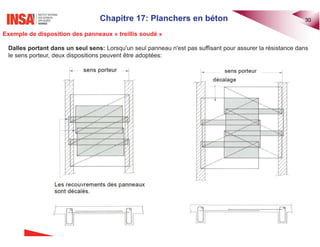
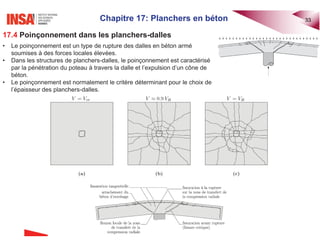
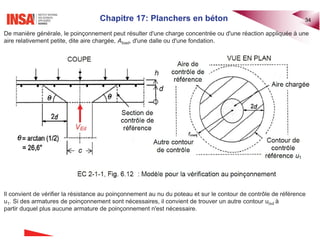
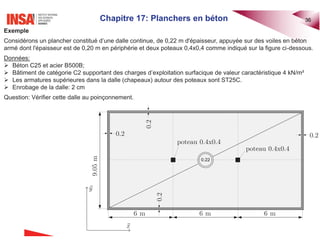
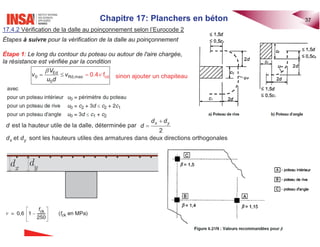
Le document traite des planchers en béton armé, abordant divers types de dalles, leur calcul des sollicitations, ainsi que des méthodes de dimensionnement. Il inclut des exemples pratiques de calcul pour les dalles bidirectionnelles continues et des analyses pour les planchers-dalles. La présentation s'appuie sur des notions théoriques et des applications concrètes en ingénierie civile.