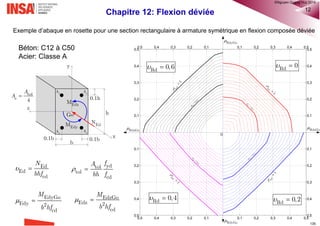
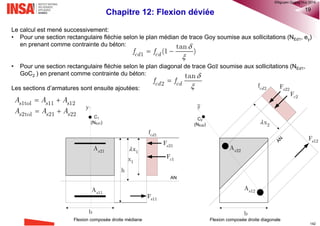
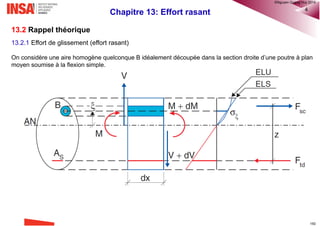
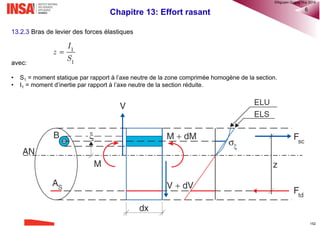
Le document est un cours sur le calcul des structures en béton armé selon l'Eurocode 2, destiné aux étudiants de 4ème année. Il couvre des sujets variés tels que les propriétés des matériaux, l'analyse structurale, et des méthodes de dimensionnement. Des chapitres spécifiques traitent également des efforts tranchants, de la flexion, de la durabilité, et des armatures.
































![Chapitre 9: Effort tranchant 29
9.5.3 Armatures d’effort tranchant minimales (EC2-1-1 §6.2.1(4) et §9.2.2)
• Même lorsque aucune armature d’effort tranchant est requise, il convient de prévoir un ferraillage transversal
minimal Asw,min. Le taux d’armatures d’effort tranchant minimales est donné par:
Asw : l’aire de la section des armatures d’effort tranchant régnant sur la longueur s
s : l’espacement des armatures d’effort tranchant, mesuré le long de l'axe longitudinal de l’élément
𝛼 : l’angle entre les armatures d’effort tranchant et l'axe longitudinal
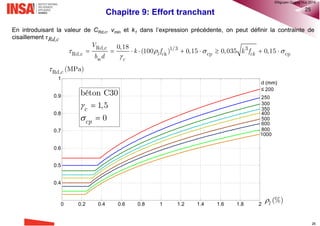
Taux minimal d'armature d'effort tranchant ρw,min [%]
cksw
w,min
w ykmin
0,081
sin
fA
s b f
C12 C16 C20 C25 C30 C35 C40 C45 C50 C55 C60 C70 C80 C90
0.055 0.064 0.072 0.080 0.088 0.095 0.101 0.107 0.113 0.119 0.124 0.134 0.143 0.152
• Ce ferraillage peut être omis dans les
éléments qui ont une capacité suffisante de
distribution transversale des charges tels
que les dalles (pleines, nervurées,
alvéolées);
• Le ferraillage minimal peut également être
omis dans les éléments secondaires
(linteaux de portée ≤ 2 m par exemple) qui
ne contribuent pas de manière significative à
la résistance et à la stabilité d'ensemble de
la structure.
®QHN2017](https://image.slidesharecdn.com/coursbaii-140129165700-phpapp02/85/Cours-Beton-Arme-II-_-Nguyen-Quang-Huy-37-320.jpg)













![Chapitre 9: Effort tranchant 43
0 1 2 3 4 5 6 7 8 9 10
-500
-400
-300
-200
-100
0
100
200
300
400
500
X: 8.504
Y: 338.6
Abscisse [m]
Efforttranchant[kN]
X: 7.208
Y: 213.4
Effort tranchant théorique
Effort tranchant de calcul
0 1 2 3 4 5 6 7 8 9 10
-500
-400
-300
-200
-100
0
100
200
300
400
500
Abscisse [m]
Efforttranchant[kN]
Effort tranchant théorique
Effort tranchant de calcul
0 1 2 3 4 5 6 7 8 9 10
-500
-400
-300
-200
-100
0
100
200
300
400
500
Abscisse [m]
Efforttranchant[kN]
Effort tranchant théorique
Effort tranchant de calcul
0 1 2 3 4 5 6 7 8 9 10
-500
-400
-300
-200
-100
0
100
200
300
400
500
Abscisse [m]
Efforttranchant[kN]
Effort tranchant théorique
Effort tranchant de calcul
0 1 2 3 4 5 6 7 8 9 10
-500
-400
-300
-200
-100
0
100
200
300
400
500
X: 1.496
Y: -312.7
Abscisse [m]
Efforttranchant[kN]
X: 2.792
Y: -197.1
Effort tranchant théorique
Effort tranchant de calcul
Tracer le diagramme de l’effort tranchant
Les armatures d’effort tranchant sont-elles nécessaires? (EC2-1-1 §6.2.2)
VEd ≥ VRd,c donc les armatures d’effort tranchant sont nécessaires.
Choisir l’angle des bielles
Afin d’optimiser les armatures d’effort tranchant on choisit
Rd,c 124.7 kNV
Rd,s,min 197.5 kNV
Quantité minimale à placer
Ed Rd,c w 2
2.5
1244 kN
1+2.5
x V b z La résistance des bielles est
surabondante
cot 2
Ed Rd,max( )V x V
®QHN2017](https://image.slidesharecdn.com/coursbaii-140129165700-phpapp02/85/Cours-Beton-Arme-II-_-Nguyen-Quang-Huy-51-320.jpg)









![Chapitre 10: Flexion simple à l’ELS 6
10.4 Prise en compte du fluage dans le calcul à l’ELS
10.4.1 Module effectif du béton
EC2-1-1§7.4.3(5)
Remarques sur la clause 7.4.3(5) de l’EC2:
• 𝜑 ∞, 𝑡0 représente le fluage final à long terme du béton donc sous des charges permanentes
• Le texte qui accompagne la définition de 𝜑 ∞, 𝑡0 précise bien qu’il s’agit d’un coefficient de fluage qui tient
compte du chargement dans un intervalle de temps considérés [t0, t]. Il faut donc comprendre qu’il est
question ici de 𝜑 𝑡, 𝑡0 puisque ce dernier permet de tenir compte non seulement des charges à long terme
(t= ∞) mais aussi à plus au moins court terme (comme les charges d’exploitation). 𝜑 𝑡, 𝑡0 doit donc être
utilisé avec la combinaison caractéristique de charges.
• Les clauses 7.2 et 7.3 des ‘‘Recommandations professionnelles pour l'application de la norme NF EN 1992-1-
1 (NF P 18-711-1) et de son annexe nationale (NF P 18-711-1/NA-Eurocode 2, partie 1-1) relatives au calcul
des structures en béton’’ stipulent que:
Eqp
, 0
Ed,ELS
avec ( , )
1
cm
c eff ef
ef
ME
E t
M
®QHN2017](https://image.slidesharecdn.com/coursbaii-140129165700-phpapp02/85/Cours-Beton-Arme-II-_-Nguyen-Quang-Huy-61-320.jpg)

















![Chapitre 10: Flexion simple à l’ELS 24
6. Si 𝑀Ed,ELS ≤ 𝑀ser il n’est pas nécessaire d’ajouter une armature comprimée: As2=0
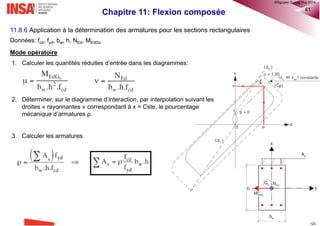
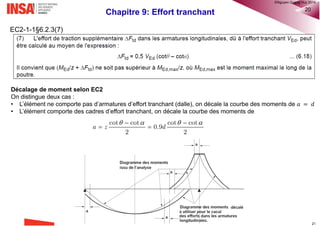
Le calcul exact de la section des armatures longitudinales tendues est assez compliqué et ne peut se faire sans
itération. Compte tenu des valeurs usuelles de hf/d1 ∈ [0,1; 0,3], on peut admettre, comme une expression
approchée du bras de levier zs, la formule suivante:
Ainsi, il est possible d’estimer la section d’acier tendu
nécessaire par:
7. Si 𝑀Ed,ELS > 𝑀ser Les contraintes limites de l’EC2 sont dépassées As2 > 0
On va calculer la quantité minimale d’armature en compression avec laquelle les limites des contraintes de l’EC2
sont respectées (pivot a-b).
On fixe:
• As1 &As2 sont calculés à l’aide des équations d’équilibre:
8. Vérifier 𝐴s1 ≥ As,min (EC2-1-1 §9.2.1.1(1)) et 𝐴s1 et As2 ≤ 0,04𝐴𝑐 (EC2-1-1 §9.2.1.1)
1 f
0.99 0.4s
z d h
sx
c c
cF
sz
Ed,ELS
s1
s s
M
A
z
s s
x x
2
2
1
s
s s
s
x d
d x
Ed,ELS ser
2
2 1 2
( )s
s
M M
A
d d
w
eff w 2 2
1
1
2 2
fs c
f c s s
s
s
s
hb x
h b b A
x
A
®QHN2017](https://image.slidesharecdn.com/coursbaii-140129165700-phpapp02/85/Cours-Beton-Arme-II-_-Nguyen-Quang-Huy-79-320.jpg)




















![Chapitre 11: Flexion composée 9
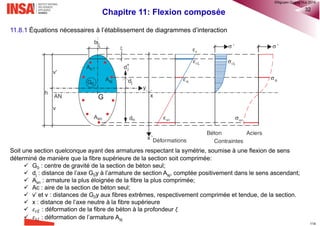
11.2.2 Cas des structures
• On remplace l’inclinaison globale θi par une force transversale égale aux composantes horizontales des
efforts normaux dans les éléments inclinés(EC2 §5.2 (8)):
système de contreventement:
plancher de contreventement:
diaphragme de toiture:
11.2.3 Prise en compte des écarts sur les dimensions des sections
• Les écarts sur les dimensions des sections sont normalement pris en compte dans les coefficients partiels
relatifs aux matériaux. En dehors du cas des sections droites avec un ferraillage symétrique, il n’y donc pas
lieu d’en tenir compte (EC2 §5.2(1)P).
• Pour tenir compte des écarts sur les dimensions des sections dans le cas des sections droites avec un
ferraillage symétrique, il convient d’adopter à l’ELU une excentricité minimale (EC2 §6.1(4)):
Le moment sollicitant au premier ordre à prendre à l’ELU est:
i i b aH N N
( ) / 2i i b aH N N
i i aH N
0,min max[20mm; / 30 ]e h
, 0Ed Go Ed EdM M e N
0 0,minavec max[ ; ]ie e e
®QHN2017](https://image.slidesharecdn.com/coursbaii-140129165700-phpapp02/85/Cours-Beton-Arme-II-_-Nguyen-Quang-Huy-102-320.jpg)