Télécharger en tant que PDF, PPTX
Téléchargé parQuang Huy Nguyen
Diagrammes d'interraction M-N Selon l'Eurocode 2
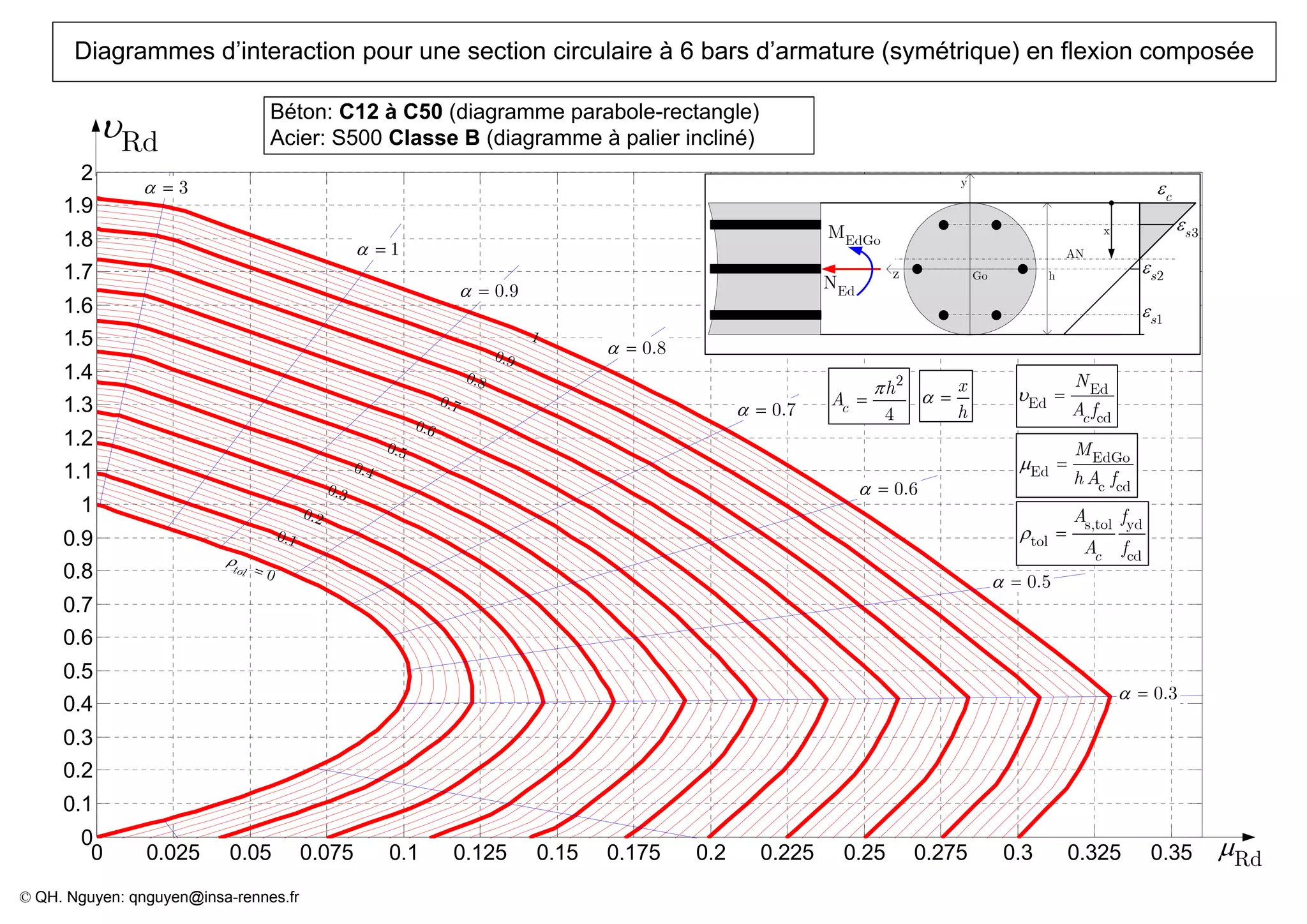
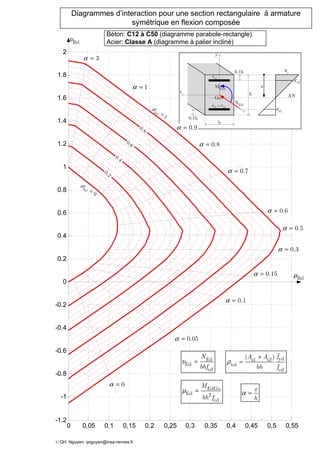
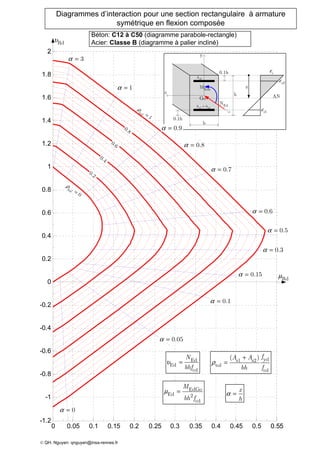
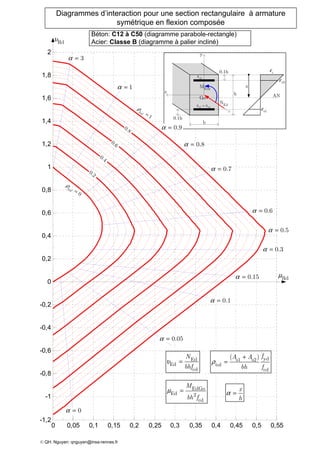
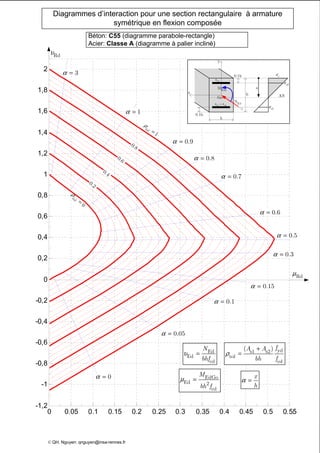
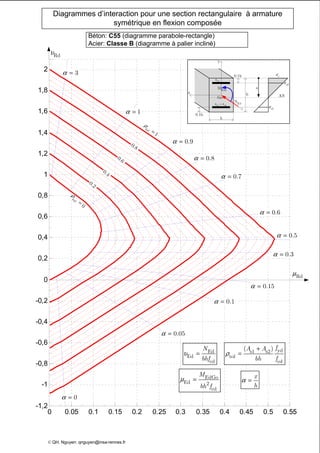
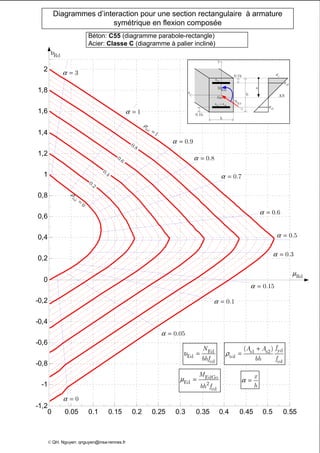
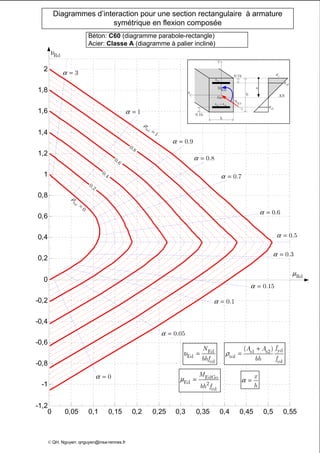
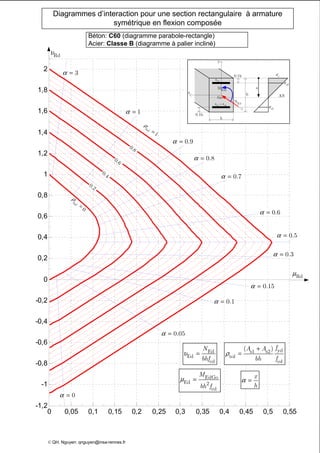
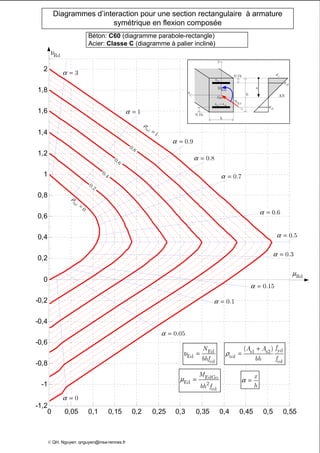
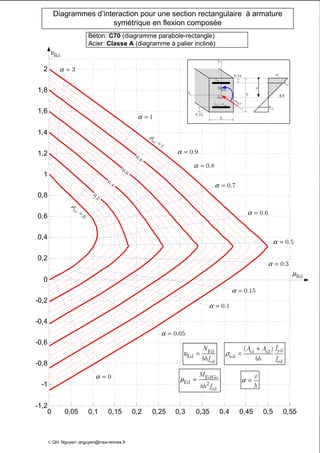
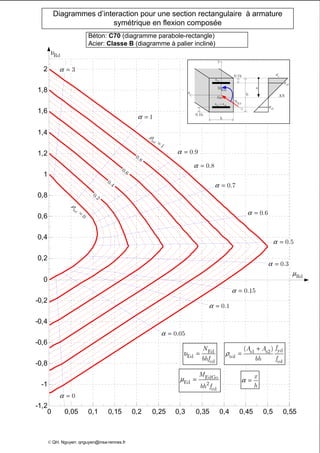
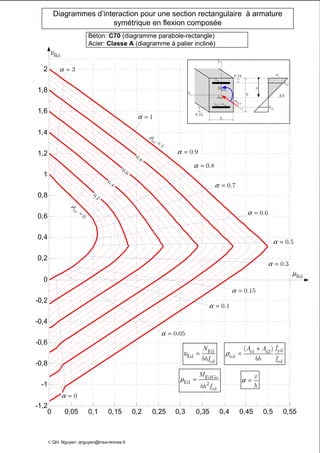
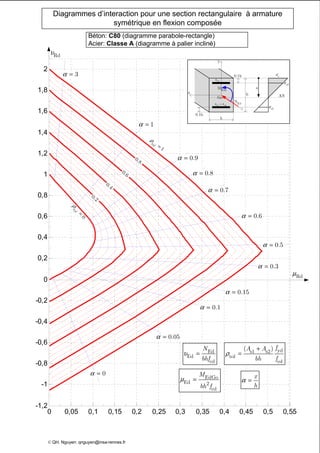
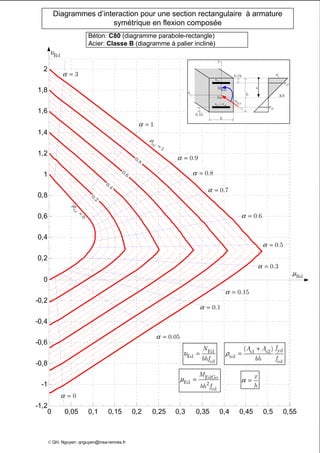
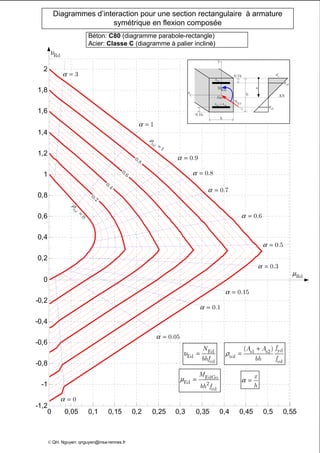
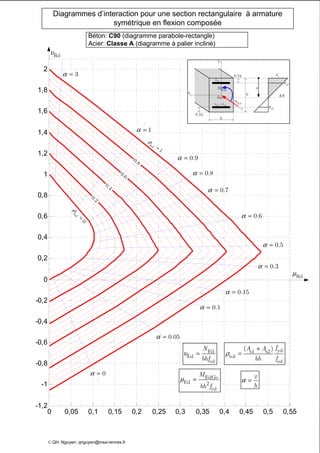
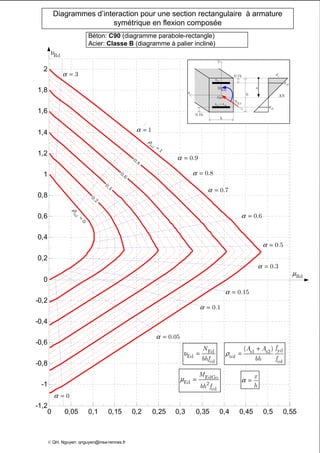
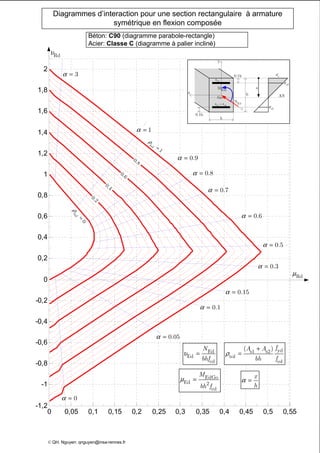
Le document présente des diagrammes d'interaction pour des sections en béton à armature symétrique sous flexion composée pour différentes classes de béton (de c12 à c70) et d'acier (classes a, b et c). Ces diagrammes incluent des représentations parabole-rectangle, illustrant les relations de résistance et déformation des matériaux. Ils sont essentiels pour le calcul et la conception d'éléments en béton armé.
![[Soutenance du PFE] Étude du flambement des poteaux selon l'EC2](https://cdn.slidesharecdn.com/ss_thumbnails/soutenancedupfe-141030050449-conversion-gate01-thumbnail.jpg?width=640&height=640&fit=bounds)
![cours stockage d'energie [Autosaved].pptx](https://cdn.slidesharecdn.com/ss_thumbnails/coursstockagedenergieautosaved-251218151955-862d0c90-thumbnail.jpg?width=640&height=640&fit=bounds)
Diagrammes d'interraction M-N Selon l'Eurocode 2
- 1. 0 0.025 0.050.075 0.1 0.125 0.15 0.175 0.2 0.225 0.25 0.275 0.3 0.325 0.35 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2 © QH. Nguyen: qnguyen@insa-rennes.fr Rd Rd Diagrammes d’interaction pour une section circulaire à 6 bars d’armature (symétrique) en flexion composée Béton: C12 à C50 (diagramme parabole-rectangle) Acier: S500 Classe B (diagramme à palier incliné) Ed Ed cdc N A f EdGo Ed c cd M h A f s,tol yd tol cdc A f A f x h 2 4c h A 0tol 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 3 1 0.9 0.8 0.7 0.6 0.5 0.3 EdGoM Ed N AN x c 3s 2sGo h 1s y z
- 2. 0 0,05 0,10,15 0,2 0,25 0,3 0,35 0,4 0,45 0,5 0,55 -1.2 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 22 z EdzM y EdN Go s2 A b 0.1h h s1 s2A A= 0.1h AN x cε 2sε 1sε Diagrammes d’interaction pour une section rectangulaire à armature symétrique en flexion composée Béton: C12 à C50 (diagramme parabole-rectangle) Acier: Classe A (diagramme à palier incliné) υ = Ed Ed cd N bhf EdGo Ed 2 cd M bh f µ = yds1 s2 tol cd ( ) fA A bh f ρ + = x h α = 3α = 1α = 0.8α = 0.7α = 0.5α = 0.3α = 0.15α = 0.1α = 0.05α = Rdµ Rdυ © QH. Nguyen: qnguyen@insa-rennes.fr 0.9α = 0α = 0.6α = ρ = 1 tol 0.8 0.6 0.4 0.2 0 tol ρ =
- 3. 0 0.05 0.10.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5 0.550.55 -1.2 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 22 z EdzM y EdN Go s2A b 0.1h h s1 s2A A= 0.1h AN x cε 2sε 1sε Diagrammes d’interaction pour une section rectangulaire à armature symétrique en flexion composée Béton: C12 à C50 (diagramme parabole-rectangle) Acier: Classe B (diagramme à palier incliné) υ = Ed Ed cd N bhf yds1 s2 tol cd ( ) fA A bh f ρ + = x h α = 3α = 1α = 0.8α = 0.7α = 0.5α = 0.3α = 0.15α = 0.1α = 0.05α = Rdµ Rdυ © QH. Nguyen: qnguyen@insa-rennes.fr 0.9α = 0α = 0.6α = ρ = 1 tol 0.8 0.6 0.4 0.2 0 tol ρ = EdGo Ed 2 cd M bh f µ =
- 4. 0 0,05 0,10,15 0,2 0,25 0,3 0,35 0,4 0,45 0,5 0,55 -1,2 -1 -0,8 -0,6 -0,4 -0,2 -0 0,2 0,4 0,6 0,8 1 1,2 1,4 1,6 1,8 2 z EdzM y EdN Go s2 A b 0.1h h s1 s2A A= 0.1h AN x cε 2sε 1sε Diagrammes d’interaction pour une section rectangulaire à armature symétrique en flexion composée Béton: C12 à C50 (diagramme parabole-rectangle) Acier: Classe B (diagramme à palier incliné) υ = Ed Ed cd N bhf EdGo Ed 2 cd M bh f µ = yds1 s2 tol cd ( ) fA A bh f ρ + = x h α = 3α = 1α = 0.8α = 0.7α = 0.5α = 0.3α = 0.15α = 0.1α = 0.05α = Rdµ Rdυ © QH. Nguyen: qnguyen@insa-rennes.fr 0.9α = 0α = 0.6α = ρ = 1 tol 0.8 0.6 0.4 0.2 0 tol ρ =
- 5. 0 0.05 0.10.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5 0.550.55 -1,2 -1 -0,8 -0,6 -0,4 -0,2 0 0,2 0,4 0,6 0,8 1 1,2 1,4 1,6 1,8 2 Diagrammes d’interaction pour une section rectangulaire à armature symétrique en flexion composée Béton: C55 (diagramme parabole-rectangle) Acier: Classe A (diagramme à palier incliné) z Edz M y EdN Go s2 A b 0.1h h s1 s2 A A= 0.1h AN x cε 2s ε 1s ε υ = Ed Ed cd N bhf EdGo Ed 2 cd M bh f µ = yds1 s2 tol cd ( ) fA A bh f ρ + = x h α = 3α = 1α = 0.8α = 0.7α = 0.5α = 0.3α = 0.15α = 0.1α = 0.05α = Rdµ © QH. Nguyen: qnguyen@insa-rennes.fr 0.9α = 0α = 0.6α = ρ = 1 tol 0.8 0.6 0.4 0.2 0 tol ρ = Rdυ
- 6. 0 0.05 0.10.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5 0.550.55 -1,2 -1 -0,8 -0,6 -0,4 -0,2 -0 0,2 0,4 0,6 0,8 1 1,2 1,4 1,6 1,8 2 Diagrammes d’interaction pour une section rectangulaire à armature symétrique en flexion composée Béton: C55 (diagramme parabole-rectangle) Acier: Classe B (diagramme à palier incliné) z Edz M y EdN Go s2 A b 0.1h h s1 s2 A A= 0.1h AN x cε 2s ε 1s ε υ = Ed Ed cd N bhf EdGo Ed 2 cd M bh f µ = yds1 s2 tol cd ( ) fA A bh f ρ + = x h α = 3α = 1α = 0.8α = 0.7α = 0.5α = 0.3α = 0.15α = 0.1α = 0.05α = Rdµ © QH. Nguyen: qnguyen@insa-rennes.fr 0.9α = 0α = 0.6α = ρ = 1 tol 0.8 0.6 0.4 0.2 0 tol ρ = Rdυ
- 7. 0 0.05 0.10.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5 0.550.55 -1,2 -1 -0,8 -0,6 -0,4 -0,2 -0 0,2 0,4 0,6 0,8 1 1,2 1,4 1,6 1,8 2 Diagrammes d’interaction pour une section rectangulaire à armature symétrique en flexion composée Béton: C55 (diagramme parabole-rectangle) Acier: Classe C (diagramme à palier incliné) z Edz M y EdN Go s2 A b 0.1h h s1 s2 A A= 0.1h AN x cε 2s ε 1s ε υ = Ed Ed cd N bhf EdGo Ed 2 cd M bh f µ = yds1 s2 tol cd ( ) fA A bh f ρ + = x h α = 3α = 1α = 0.8α = 0.7α = 0.5α = 0.3α = 0.15α = 0.1α = 0.05α = Rdµ © QH. Nguyen: qnguyen@insa-rennes.fr 0.9α = 0α = 0.6α = ρ = 1 tol 0.8 0.6 0.4 0.2 0 tol ρ = Rdυ
- 8. 0 0,05 0,10,15 0,2 0,25 0,3 0,35 0,4 0,45 0,5 0,55 -1,2 -1 -0,8 -0,6 -0,4 -0,2 0 0,2 0,4 0,6 0,8 1 1,2 1,4 1,6 1,8 2 Diagrammes d’interaction pour une section rectangulaire à armature symétrique en flexion composée Béton: C60 (diagramme parabole-rectangle) Acier: Classe A (diagramme à palier incliné) z Edz M y EdN Go s2 A b 0.1h h s1 s2 A A= 0.1h AN x cε 2s ε 1s ε υ = Ed Ed cd N bhf EdGo Ed 2 cd M bh f µ = yds1 s2 tol cd ( ) fA A bh f ρ + = x h α = 3α = 1α = 0.8α = 0.7α = 0.5α = 0.3α = 0.15α = 0.1α = 0.05α = Rdµ © QH. Nguyen: qnguyen@insa-rennes.fr 0.9α = 0α = 0.6α = ρ = 1 tol 0.8 0.6 0.4 0.2 0 tol ρ = Rdυ
- 9. 0 0,05 0,10,15 0,2 0,25 0,3 0,35 0,4 0,45 0,5 0,55 -1,2 -1 -0,8 -0,6 -0,4 -0,2 0 0,2 0,4 0,6 0,8 1 1,2 1,4 1,6 1,8 2 Diagrammes d’interaction pour une section rectangulaire à armature symétrique en flexion composée Béton: C60 (diagramme parabole-rectangle) Acier: Classe B (diagramme à palier incliné) z Edz M y EdN Go s2 A b 0.1h h s1 s2 A A= 0.1h AN x cε 2s ε 1s ε υ = Ed Ed cd N bhf EdGo Ed 2 cd M bh f µ = yds1 s2 tol cd ( ) fA A bh f ρ + = x h α = 3α = 1α = 0.8α = 0.7α = 0.5α = 0.3α = 0.15α = 0.1α = 0.05α = Rdµ © QH. Nguyen: qnguyen@insa-rennes.fr 0.9α = 0α = 0.6α = ρ = 1 tol 0.8 0.6 0.4 0.2 0 tol ρ = Rdυ
- 10. 0 0,05 0,10,15 0,2 0,25 0,3 0,35 0,4 0,45 0,5 0,55 -1,2 -1 -0,8 -0,6 -0,4 -0,2 0 0,2 0,4 0,6 0,8 1 1,2 1,4 1,6 1,8 2 Diagrammes d’interaction pour une section rectangulaire à armature symétrique en flexion composée Béton: C60 (diagramme parabole-rectangle) Acier: Classe C (diagramme à palier incliné) z Edz M y EdN Go s2 A b 0.1h h s1 s2 A A= 0.1h AN x cε 2s ε 1s ε υ = Ed Ed cd N bhf EdGo Ed 2 cd M bh f µ = yds1 s2 tol cd ( ) fA A bh f ρ + = x h α = 3α = 1α = 0.8α = 0.7α = 0.5α = 0.3α = 0.15α = 0.1α = 0.05α = Rdµ © QH. Nguyen: qnguyen@insa-rennes.fr 0.9α = 0α = 0.6α = ρ = 1 tol 0.8 0.6 0.4 0.2 0 tol ρ = Rdυ
- 11. 0 0,05 0,10,15 0,2 0,25 0,3 0,35 0,4 0,45 0,5 0,55 -1,2 -1 -0,8 -0,6 -0,4 -0,2 0 0,2 0,4 0,6 0,8 1 1,2 1,4 1,6 1,8 2 Diagrammes d’interaction pour une section rectangulaire à armature symétrique en flexion composée Béton: C70 (diagramme parabole-rectangle) Acier: Classe A (diagramme à palier incliné) z Edz M y EdN Go s2 A b 0.1h h s1 s2 A A= 0.1h AN x cε 2s ε 1s ε υ = Ed Ed cd N bhf EdGo Ed 2 cd M bh f µ = yds1 s2 tol cd ( ) fA A bh f ρ + = x h α = 3α = 1α = 0.8α = 0.7α = 0.5α = 0.3α = 0.15α = 0.1α = 0.05α = Rdµ © QH. Nguyen: qnguyen@insa-rennes.fr 0.9α = 0α = 0.6α = ρ = 1 tol 0.8 0.6 0.4 0.2 0 tol ρ = Rdυ
- 12. 0 0,05 0,10,15 0,2 0,25 0,3 0,35 0,4 0,45 0,5 0,55 -1,2 -1 -0,8 -0,6 -0,4 -0,2 0 0,2 0,4 0,6 0,8 1 1,2 1,4 1,6 1,8 2 Diagrammes d’interaction pour une section rectangulaire à armature symétrique en flexion composée Béton: C70 (diagramme parabole-rectangle) Acier: Classe B (diagramme à palier incliné) z Edz M y EdN Go s2 A b 0.1h h s1 s2 A A= 0.1h AN x cε 2s ε 1s ε υ = Ed Ed cd N bhf EdGo Ed 2 cd M bh f µ = yds1 s2 tol cd ( ) fA A bh f ρ + = x h α = 3α = 1α = 0.8α = 0.7α = 0.5α = 0.3α = 0.15α = 0.1α = 0.05α = Rdµ © QH. Nguyen: qnguyen@insa-rennes.fr 0.9α = 0α = 0.6α = ρ = 1 tol 0.8 0.6 0.4 0.2 0 tol ρ = Rdυ
- 13. 0 0,05 0,10,15 0,2 0,25 0,3 0,35 0,4 0,45 0,5 0,55 -1,2 -1 -0,8 -0,6 -0,4 -0,2 0 0,2 0,4 0,6 0,8 1 1,2 1,4 1,6 1,8 2 Diagrammes d’interaction pour une section rectangulaire à armature symétrique en flexion composée Béton: C70 (diagramme parabole-rectangle) Acier: Classe A (diagramme à palier incliné) z Edz M y EdN Go s2 A b 0.1h h s1 s2 A A= 0.1h AN x cε 2s ε 1s ε υ = Ed Ed cd N bhf EdGo Ed 2 cd M bh f µ = yds1 s2 tol cd ( ) fA A bh f ρ + = x h α = 3α = 1α = 0.8α = 0.7α = 0.5α = 0.3α = 0.15α = 0.1α = 0.05α = Rdµ © QH. Nguyen: qnguyen@insa-rennes.fr 0.9α = 0α = 0.6α = ρ = 1 tol 0.8 0.6 0.4 0.2 0 tol ρ = Rdυ
- 14. 0 0,05 0,10,15 0,2 0,25 0,3 0,35 0,4 0,45 0,5 0,55 -1,2 -1 -0,8 -0,6 -0,4 -0,2 0 0,2 0,4 0,6 0,8 1 1,2 1,4 1,6 1,8 2 Diagrammes d’interaction pour une section rectangulaire à armature symétrique en flexion composée Béton: C80 (diagramme parabole-rectangle) Acier: Classe A (diagramme à palier incliné) z Edz M y EdN Go s2 A b 0.1h h s1 s2 A A= 0.1h AN x cε 2s ε 1s ε υ = Ed Ed cd N bhf EdGo Ed 2 cd M bh f µ = yds1 s2 tol cd ( ) fA A bh f ρ + = x h α = 3α = 1α = 0.8α = 0.7α = 0.5α = 0.3α = 0.15α = 0.1α = 0.05α = Rdµ © QH. Nguyen: qnguyen@insa-rennes.fr 0.9α = 0α = 0.6α = ρ = 1 tol 0.8 0.6 0.4 0.2 0 tol ρ = Rdυ
- 15. 0 0,05 0,10,15 0,2 0,25 0,3 0,35 0,4 0,45 0,5 0,55 -1,2 -1 -0,8 -0,6 -0,4 -0,2 0 0,2 0,4 0,6 0,8 1 1,2 1,4 1,6 1,8 2 Diagrammes d’interaction pour une section rectangulaire à armature symétrique en flexion composée Béton: C80 (diagramme parabole-rectangle) Acier: Classe B (diagramme à palier incliné) z Edz M y EdN Go s2 A b 0.1h h s1 s2 A A= 0.1h AN x cε 2s ε 1s ε υ = Ed Ed cd N bhf EdGo Ed 2 cd M bh f µ = yds1 s2 tol cd ( ) fA A bh f ρ + = x h α = 3α = 1α = 0.8α = 0.7α = 0.5α = 0.3α = 0.15α = 0.1α = 0.05α = Rdµ © QH. Nguyen: qnguyen@insa-rennes.fr 0.9α = 0α = 0.6α = ρ = 1 tol 0.8 0.6 0.4 0.2 0 tol ρ = Rdυ
- 16. 0 0,05 0,10,15 0,2 0,25 0,3 0,35 0,4 0,45 0,5 0,55 -1,2 -1 -0,8 -0,6 -0,4 -0,2 0 0,2 0,4 0,6 0,8 1 1,2 1,4 1,6 1,8 2 Diagrammes d’interaction pour une section rectangulaire à armature symétrique en flexion composée Béton: C80 (diagramme parabole-rectangle) Acier: Classe C (diagramme à palier incliné) z Edz M y EdN Go s2 A b 0.1h h s1 s2 A A= 0.1h AN x cε 2s ε 1s ε υ = Ed Ed cd N bhf EdGo Ed 2 cd M bh f µ = yds1 s2 tol cd ( ) fA A bh f ρ + = x h α = 3α = 1α = 0.8α = 0.7α = 0.5α = 0.3α = 0.15α = 0.1α = 0.05α = Rdµ © QH. Nguyen: qnguyen@insa-rennes.fr 0.9α = 0α = 0.6α = ρ = 1 tol 0.8 0.6 0.4 0.2 0 tol ρ = Rdυ
- 17. 0 0,05 0,10,15 0,2 0,25 0,3 0,35 0,4 0,45 0,5 0,55 -1,2 -1 -0,8 -0,6 -0,4 -0,2 0 0,2 0,4 0,6 0,8 1 1,2 1,4 1,6 1,8 2 Diagrammes d’interaction pour une section rectangulaire à armature symétrique en flexion composée Béton: C90 (diagramme parabole-rectangle) Acier: Classe A (diagramme à palier incliné) z Edz M y EdN Go s2 A b 0.1h h s1 s2 A A= 0.1h AN x cε 2s ε 1s ε υ = Ed Ed cd N bhf EdGo Ed 2 cd M bh f µ = yds1 s2 tol cd ( ) fA A bh f ρ + = x h α = 3α = 1α = 0.8α = 0.7α = 0.5α = 0.3α = 0.15α = 0.1α = 0.05α = Rdµ © QH. Nguyen: qnguyen@insa-rennes.fr 0.9α = 0α = 0.6α = ρ = 1 tol 0.8 0.6 0.4 0.2 0 tol ρ = Rdυ
- 18. 0 0,05 0,10,15 0,2 0,25 0,3 0,35 0,4 0,45 0,5 0,55 -1,2 -1 -0,8 -0,6 -0,4 -0,2 0 0,2 0,4 0,6 0,8 1 1,2 1,4 1,6 1,8 2 Diagrammes d’interaction pour une section rectangulaire à armature symétrique en flexion composée Béton: C90 (diagramme parabole-rectangle) Acier: Classe B (diagramme à palier incliné) z Edz M y EdN Go s2 A b 0.1h h s1 s2 A A= 0.1h AN x cε 2s ε 1s ε υ = Ed Ed cd N bhf EdGo Ed 2 cd M bh f µ = yds1 s2 tol cd ( ) fA A bh f ρ + = x h α = 3α = 1α = 0.8α = 0.7α = 0.5α = 0.3α = 0.15α = 0.1α = 0.05α = Rdµ © QH. Nguyen: qnguyen@insa-rennes.fr 0.9α = 0α = 0.6α = ρ = 1 tol 0.8 0.6 0.4 0.2 0 tol ρ = Rdυ
- 19. 0 0,05 0,10,15 0,2 0,25 0,3 0,35 0,4 0,45 0,5 0,55 -1,2 -1 -0,8 -0,6 -0,4 -0,2 0 0,2 0,4 0,6 0,8 1 1,2 1,4 1,6 1,8 2 Diagrammes d’interaction pour une section rectangulaire à armature symétrique en flexion composée Béton: C90 (diagramme parabole-rectangle) Acier: Classe C (diagramme à palier incliné) z Edz M y EdN Go s2 A b 0.1h h s1 s2 A A= 0.1h AN x cε 2s ε 1s ε υ = Ed Ed cd N bhf EdGo Ed 2 cd M bh f µ = yds1 s2 tol cd ( ) fA A bh f ρ + = x h α = 3α = 1α = 0.8α = 0.7α = 0.5α = 0.3α = 0.15α = 0.1α = 0.05α = Rdµ © QH. Nguyen: qnguyen@insa-rennes.fr 0.9α = 0α = 0.6α = ρ = 1 tol 0.8 0.6 0.4 0.2 0 tol ρ = Rdυ