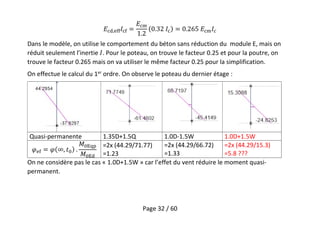
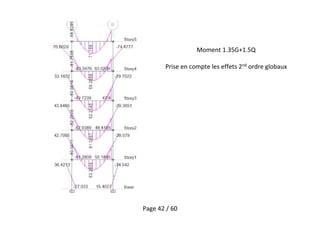
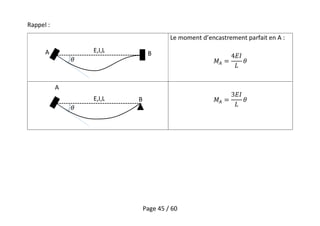
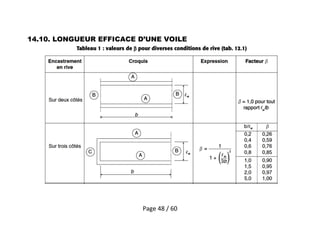
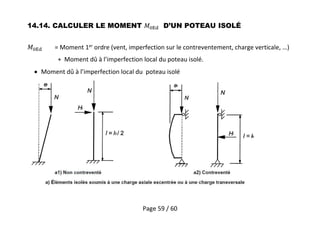
Le document traite des effets du second ordre sur les poteaux dans les structures en génie civil, en se concentrant sur la force critique d'Euler et les implications liées à la stabilité des poteaux isolés contreventés et non-contreventés. Il décrit également les méthodes de calcul selon l'Eurocode, en tenant compte des imperfections géométriques et des matériaux non linéaires. Enfin, des exemples analytiques illustrent l'amplification des moments et la nécessité d'évaluer les effets globaux du second ordre pour garantir la sécurité structurelle.

1. Page 1 / 60
EFFET 2ND
ORDRE
D’UN POTEAU
Sovanvichet LIM, Dr., P.E.

2. Page 2 / 60
14.1. Force critique d’Euler
•
•
• On pose
• Solution générale:
• Conditions aux limites:
•
•
• A =0 : structure stable
• Ou
• Nous en déduisons qu’il y a une infinité
de déformées non rectilignes stables
vérifiant :
𝐹
𝐹
A
B
𝑀
𝑥
𝑦

3. Page 3 / 60
Les valeurs correspondantes de la force F sont données
par :
• Pour n=1
S’appelle la force critique d’Euler du 1er
mode de
flambement.
Si la charge appliquée est égale à la charge critique
d’Euler, le poteau devient instable.
En pratique, pour être en sécurité, on limite la charge
inférieure à la charge critique d’Euler.

4. Page 4 / 60
14.2. Effets 2nd
ordres pour un poteau isolé
Moment en bas du poteau:
- Analyse 1er
ordre: HL
- Analyse 2nd
ordre: HL+f(P)+g(P)
Les contributions de P et  sur les réponses (M,N,V,…) de
la structure s’appellent effet P- (Effet 2nd
ordre globale).
Les contributions de P et  sur les réponses (M,N,V,…) de
la structure s’appellent effet P- (Effet 2nd
ordre locale).
H
P



5. Page 5 / 60
Exemple analytique sur l’amplification de la déformée d’un poteau
isolé contreventé
𝑃
𝑞
𝐿
Poteau
déformé
𝑃
𝑃
qL/
A
B
𝑀
𝑥
𝑦
𝑞

6. Page 6 / 60
• Conditions aux limites

7. Page 7 / 60
0.00
50.00
100.00
150.00
200.00
250.00
300.00
350.00
0.00 1,000.00 2,000.00 3,000.00 4,000.00 5,000.00 6,000.00
M(kNm)
P (kN)

8. Page 8 / 60
• 200 GPa ; 20100 cm4
; 8.5 m; 3.0 kN/m
P (kN) 500 1000 2000
P-Delta M (kNm) 29.88 33.30 43.07
1st
Order M (kNm) 27.09 27.09 27.09
On observe qu’il y a une augmentation des moments
dans le poteau si on augmente la force P.
𝑃
𝑞
𝐿
Poteau
déformé
𝑃
𝑃
qL/
A
B
𝑀
𝑥
𝑦
𝑞

9. Page 9 / 60
0.00
50.00
100.00
150.00
200.00
250.00
300.00
350.00
400.00
450.00
3.00 4.00 5.00 6.00 7.00 8.00 9.00 10.00
M(kNm)
L (m)

10. Page 10 / 60
Exemple analytique sur l’amplification de la déformée d’un poteau
isolé non-contreventé
/
B
A

11. Page 11 / 60
𝑦(0) = 0 ⟹ 𝐴 −
𝐹𝐿 + 𝑃∆
𝑃
= 0 ⟹ 𝐴 =
𝐹𝐿 + 𝑃∆
𝑃
𝑦 (0) = 0 ⟹ 𝐵
𝑃
𝐸𝐼
−
𝐹
𝑃
= 0 ⟹ 𝐵 =
𝐹
𝑃
𝐸𝐼
𝑃
⟹ 𝑀 = 𝐴𝑃 cos
𝑃
𝐸𝐼
𝑥 + 𝐵𝑃 sin
𝑃
𝐸𝐼
𝑥
𝑀( 𝐿) = 0 ⟹ 𝐴𝑃 cos
𝑃
𝐸𝐼
𝐿 + 𝐵𝑃 sin
𝑃
𝐸𝐼
𝐿 = 0
𝑀 = 𝐴𝑃 cos
𝑃
𝐸𝐼
𝑥 + 𝐵𝑃 sin
𝑃
𝐸𝐼
𝑥
𝑦 = 𝐴 cos
𝑃
𝐸𝐼
𝑥 + 𝐵 sin
𝑃
𝐸𝐼
𝑥 −
𝐹
𝑃
𝑥 − 𝐴
𝐴 = −
𝐹
𝑃
𝐸𝐼
𝑃
tan
𝑃
𝐸𝐼
𝐿 ; 𝐵 =
𝐹
𝑃
𝐸𝐼
𝑃

12. Page 12 / 60
• =200 GPa ; =20100 cm4
; =8.5 m; 4.5 kN
P (kN) 450 650 890
P-Delta M (kNm) 53.52 66.35 95.71
1st Order M (kNm) 38.25 38.25 38.25
On observe qu’il y a une augmentation des moments
dans le poteau si on augmente la force P.
B
A

13. Page 13 / 60
14.3. Effets 2nd
ordre dans une structure- Définition
 Effets 2nd
ordre global vs effets 2nd
ordre local d’un élément isolé
 Effet 2nd
ordre global : Dans cet exemple:
 Le mode d’effondrement de la structure est considéré
comme le flambement d’un poteau encastré en pied
 Tous ensembles des poteaux et des poutres participent
pour assurer la stabilité globale de la structure.
 L’effet du déplacement latéral de la structure, à l’instant de
l’effondrement, sur les efforts internes peut être significatif
et non négligeable. Cet effet s’appelle « effet 2nd
ordre
global » (Sway structure)A
D

14. Page 14 / 60
Effet 2nd
ordre local / élément isolé
Un autre exemple :
Soit un poteau de la structure bi-articulé à
l’extrémité.
Le mode d’effondrement de la structure est
commencé par un effondrement d’un seul poteau ;
pendant cet instant-là, la structure ne déplace pas
latéralement significativement. (Non-sway
structure)
Dans le calcul, Le poteau peut être considéré
comme un élément isolé.
Le poteau dans cet exemple, ne participe pas dans
le contreventement de la structure pour résister
l’instabilité globale de la structure. On appelle ce
poteau « poteau contreventé ». (Braced column)

15. Page 15 / 60
Définition : Poteau contreventé vs poteau non-contreventé
 Poteau (3) = poteau contreventé (Braced column). Poteau (3) est contreventé par poteaux
(1), (2) et (4). Poteau (3) ne participe pas dans le système contre de le déplacement
latéral.
 Poteau (1), (2) et (4) = poteaux non-contreventés (Unbraced column). Poteau (1), (2) et (4)
est un élément de contreventement. Portique ABCD est stable latéralement dû à la
contribution de (1), (2) et (4).
(1) (2) (3) (4)
A B
CD

16. Page 16 / 60
ELEMENT ISOLE
 Éléments isolés : éléments effectivement isolés, ou bien éléments d'une structure pouvant
être traités comme tels pour les besoins du calcul ;

17. Page 17 / 60
 Le poteau AB, fait partie du contreventement, donc « poteau non-contreventé »
(Unbraced column)
 Mode a : On a des cas où le poteau AB est mal-dimensionné, le mode d’effondrement
global n’a pas lieu, mais seulement l’effondrement du poteau AB. Dans ce cas-là, l’effet 2nd
ordre global est négligeable (Non-sway structure). Le poteau AB peut être dimensionné
comme un « poteau isolé contreventé».
 Mode b : Le mode d’effondrement global a lieu (Sway structure). Le poteau AB peut être
dimensionné comme un « poteau isolé non-contreventé» (Mais avec certain modification,
on peut toujours le dimensionner comme un poteau isolé contreventé).
(b)
(a)
A
B B
A

18. Page 18 / 60
14.4. Effets 2nd
ordre- Méthode Eurocode
 Pour calculer les effets 2nd
ordre, il faut prendre en compte
o de la fissuration,
o de la non-linéarité des matériaux et
o du fluage
sur le comportement global. Ceci s'applique également aux éléments adjacents
intervenant dans l'analyse — poutres, dalles ou fondations, par exemple.
 Il faut aussi prendre en compte dans le calcul, les effets des imperfections géométriques.
L’Eurocode 2 nous donne 2 méthodes de calcul :
1. Méthode générale [Voir 5.8.6]
2. Méthode simplifiée

19. Page 19 / 60
Méthode simplifiée
Imperfection géométrique sur
le contreventement (Eq. 5.4)
Réduction de la rigidité de
section (5.8.7.2), (5.8.2(2)-Note)
Méthode P-Δ
Non-négligeable
Analyse structure globale
Méthode Linéaire Élastique
Analyse 1er ordre
Vérifier si l’effet global 2nd ordre est
négligeable (H.1 )
Négligeable
Calcul les efforts horizontaux
majoré pour les effets 2nd
ordre globale. (Eq. H.8)
Analyse 1er ordre
M-N-V 2nd ordre globale
M-N-V 2nd ordre globale
Analysestructureglobale(P-Δ)
Calcul comme un poteau isolé contreventé : ℓ =(Eq. 5.15) Isolé Non-contreventé: ℓ =(Eq. 5.16)
Poteau contreventé ?
Oui Non

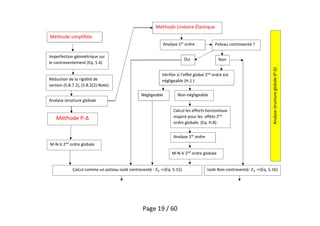
20. Page 20 / 60
Dimensionnementd’unpoteauisolé(P-δ)
Vérifier si l’effet 2nd ordre local est négligeable ? (5.8.3.1(1))
Négligeable Non-Négligeable
Méthode basée sur une
rigidité nominale [5.8.7]
Méthode basée sur une
courbure nominale [5.8.8]
𝑀 Vérifier la section

21. Page 21 / 60
14.5. Effet de l’imperfection géométrique sur le
contreventement/portique
nombre d'éléments verticaux
transmettant la force horizontale appliquée
au système de contreventement.

22. Page 22 / 60
14.6. RIGIDITE NOMINALE
o Elément comprimée : Section [5.8.7.2 (1)]
o Elément adjacent (poutre, dalle) : Section [5.8.7.2 (4)]
14.6.1 RIGIDITE NOMINALE D’UN ELEMENT COMPRIME
 C’est la réduction de la rigidité pour la prise en compte des effets de la fissuration, de la
non-linéarité des matériaux et du fluage.
 La rigidité nominale d'éléments élancés, de section droite quelconque, travaillant en
compression, peut être estimée de la manière suivante :
(Eq. 5.21)
.
Valeur recommandée, [NF][BS] :
où :
 est la valeur de calcul du module d'élasticité du béton, voir 5.8.6 (3)
 est le moment d'inertie de la section droite de béton (section grosse)
 est la valeur de calcul du module d'élasticité de l'acier,

23. Page 23 / 60
 est le moment d'inertie de la section d'armatures par rapport au centre de la
section de béton
 est un coefficient tenant compte des effets de la fissuration, du fluage etc., voir
5.8.7.2 (2) ou (3)
 est un coefficient tenant compte de la contribution des armatures, voir 5.8.7.2 (2)
ou (3).
 VALEUR SIMPLIFIEE :
Cette simplification peut convenir dans le premier pas d'itération, et est suivie par un calcul
plus précis comme indiqué en (5.8.7.2(2)).
Pour , on peut prendre
(Eq. 5.26)

24. Page 24 / 60
 VALEUR RIGOUREUSE :
Pour , on peut prendre
(Eq. 5.22)
(Eq. 5.23)
(Eq. 5.24)

25. Page 25 / 60
14.6.2 RIGIDITE NOMINALE D’UN ELEMENT ADJACENT [5.8.7.2 (4)]
Pour les poutres (et dalles), de manière simplifiée, on peut admettre que les sections sont
entièrement fissurées. Il convient d'établir la rigidité sur la base d'un module effectif du béton :
,
.
est le coefficient de fluage effectif ; on peut utiliser la même valeur que pour les poteaux.
On utilise la méthode classique utilisée pour l’ELS pour calculer l’inertie de la section fissurée.

26. Page 26 / 60
14.6.3 COEFFICIENT DE FLUAGE:
est le moment fléchissant du premier ordre dans le
cas de la combinaison quasi-permanente de charges (ELS)
est le moment fléchissant du premier ordre dans le cas
de la combinaison de charges de calcul (ELU)
(Eq. 5.19)
Si varie dans l'élément ou la structure, on peut soit calculer le
rapport pour la section de moment maximal soit utiliser une valeur
moyenne représentative.
[5.8.4(3)]
L'effet du fluage peut être ignoré, ce qui revient à admettre , si
toutes les trois conditions suivantes sont satisfaites :



Ici, est le moment du premier ordre et est la hauteur de la section
dans la direction correspondante.
[5.8.4(4)]

27. Page 27 / 60
La déformation totale sous la charge à longterme peut être directement déterminé en utilisant
le module équivalent pour le béton , ce qui correspond à la ligne AC dans le
figure 5.20.
La déformation totale sous la charge de calcule (à ELU) peut être calculée de la même façon si
le ratio du fluage efficace est utilisé, ligne AD dans le figure Fig. 5.20. Le module efficace du
béton doit être où est le coefficient de fluage efficace.

28. Page 28 / 60
14.7. Vérifier si l’effet 2nd
ordre global est négligeable
 On peut négliger les effets globaux du second ordre dans les bâtiments lorsque :
, , (H.6)
Où
, est la charge verticale totale (sur les éléments contreventés et les éléments de
contreventement)
, est la charge globale de flambement prenant en compte la flexion et l’effort
tranchant globaux, obtenu par l’analyse de flambement (Buckling analysis).

29. Page 29 / 60
14.8. Calcul des efforts horizontaux majoré pour les effets 2nd
ordre
globale
 On calcule les effets globales 2nd
ordre en appliquant les forces horizontaux fictifs majorée
,
,
,
,
,
(H.8)
où
, est la force horizontale du premier ordre due au vent, aux imperfections, etc.
, est la charge verticale totale sur les éléments de contreventement et sur la
structure porteuse
, est la charge globale nominale de flambement

30. Page 30 / 60
Exemple
Vérifier si les effets globaux du 2nd
ordre sont négligeables.
5m
5x3.6m
15kN
15kN
15kN
15kN
15kN
DL = 30 kN/m
LL= 8 kN/m
Vent 15 kN par étage
Poutre BR30x40 As=226mm2
;
Poteau C40x40
,

31. Page 31 / 60
1er
Calcul :
. .
Dans ce 1er
étape de calcule, on suppose que .
 Pour les poteaux :
 Pour les poutres :
Poutre 30x40 avec As = 226 mm2
, l’inertie fissurée est :
Inertie de la section grosse (sans prise en compte des armatures) est :

32. Page 32 / 60
,
Dans le modèle, on utilise le comportement du béton sans réduction du module E, mais on
réduit seulement l’inertie . Pour le poteau, on trouve le facteur 0.25 et pour la poutre, on
trouve le facteur 0.265 mais on va utiliser le même facteur 0.25 pour la simplification.
On effectue le calcul du 1er
ordre. On observe le poteau du dernier étage :
Quasi-permanente 1.35D+1.5Q 1.0D-1.5W 1.0D+1.5W
=2x (44.29/71.77)
=1.23
=2x (44.29/66.72)
=1.33
=2x (44.29/15.3)
=5.8 ???
On ne considère pas le cas « 1.0D+1.5W » car l’effet du vent réduire le moment quasi-
permanent.

33. Page 33 / 60
Pour le poteau au rez-de-chaussé :
Quasi-permanente 1.35D+1.5Q 1.0D-1.5W
2x (21.29/34.49)
=1.23
2x (12.7/20.58)
=1.23
2x (21.29/55.48)
=0.77
2x (12.7/156.05)
=0.16
La valeur de  1.2. On peut calculer pour une section de moment maximum
et utilise cette valeur pour tous les autres poteaux de la structure.

34. Page 34 / 60

35. Page 35 / 60
2e
Calcul : Pour = 1.2
 Pour les poteaux :
 Pour les poutres :
,
Dans le modèle, on effectue la réduction de 0.156 pour le poteau, et 0.116 pour les poutres.
 Imperfection sur le système de contreventement

36. Page 36 / 60
Le nombre de poteau transmettant les charges horizontaux m = 10
Etage
G Q
N (kN) Hi (kN)* N (kN) Hi (kN)*
E5 0.37 0.1
E4 75 0.37 20 0.1
E3 150 0.37 40 0.1
E2 225 0.37 60 0.1
E1 300 0.37 80 0.1
E0 375 100
(*) Multiplier par 2 pour deux poteaux identiques par étage.

37. Page 37 / 60

38. Page 38 / 60
On effectue le calcul du 1er
ordre en considérant l’imperfection. On observe le poteau du
dernier étage :
Quasi-permanente 1.35D+1.5Q 1.0D-1.5W
=2x (47.12/76.35)
= 1.23
=2x (47.12/71.94)
=1.3
On observe que la valeur de ne change pas beaucoup. On adopte cette valeur de .

39. Page 39 / 60
3e
Vérifier si l’effet 2nd
ordre globale est négligeable
On effectue l’analyse de flambement pour la combinaison : « 1.35D+1.5Q ».

40. Page 40 / 60
Mode 1 : facteur=4.45 Mode 2 : facteur=7.61 Mode 2 : facteur=11.55
,
,

41. Page 41 / 60
On obtient , , , les effets 2nd
ordres globaux n’est pas négligeable
Les forces horizontaux fictifs majorée pour prendre en compte les effets 2nd
ordres globaux,
sont défini par
,
,
,
,
Le facteur de l’amplification de la charge horizontale est :
,
,
On effectue une autre calcule 1er
ordre avec l’effort du vent et de l’imperfection augmenté par
le facteur 1.3.

42. Page 42 / 60
Moment 1.35G+1.5Q
Prise en compte les effets 2nd
ordre globaux

43. Page 43 / 60
14.9. LONGUEUR EFFICACE D’UN POTEAU ISOLE
Poteau isolé contreventé :
(Eq. 5.15)
Poteau isolé non-contreventé :
(Eq. 5.16)
, sont les souplesses relatives des encastrements partiels
aux extrémités 1 et 2 respectivement :
est la rotation des éléments (poutre) s'opposant à la rotation
pour le moment fléchissant M ;
est la rigidité en flexion de l'élément comprimé
est la hauteur libre de l'élément comprimé entre liaisons
d'extrémité

44. Page 44 / 60
• CALCULER LE FACTEUR 𝟏 ET 𝟐
• est la limite théorique correspondant à l'encastrement parfait et ∞ est la
limite correspondant à un appui parfaitement libre.
• L'encastrement parfait étant rare dans la pratique, on recommande une valeur minimale
de 0.1 pour et .
• Si un élément comprimé adjacent (poteau), dans un nœud, est susceptible de contribuer à
la rotation au flambement, alors il convient de remplacer dans la définition de
par , a et b représentant respectivement l'élément comprimé
(poteau) situé au-dessus et l'élément comprimé situé au-dessous du nœud.
• Pour la définition des longueurs efficaces, il convient de tenir compte de l'effet de la
fissuration dans la rigidité des éléments s'opposant à la déformation, sauf s'il peut être
démontré que ceux-ci sont non fissurés à l'ELU.
• du poteau dans le calcul de , est basé sur la section fissurée ? ou la rigidité
nominale ?

45. Page 45 / 60
Rappel :
Le moment d’encastrement parfait en A :
A BE,I,L
A
BE,I,L

46. Page 46 / 60
Exemple :
Question : Pour le poteau AD,
 est ce qu’il bloque la rotation en A comme les poutres AB et AC ?
 ou les poutres AB et AC bloquent les poteaux AD et AE ?
Eb, Ib1, L1Eb, Ib2, L2
Ec, Ic, Lc
Ec, Ica, Lca
Pour une rotation en (A):
Moment total résistant la rotation est
A
BC
D
E

47. Page 47 / 60
Réponse :
 Si le flambement dans le poteau AD et le poteau AE ont lieu en même temps, on ne
considère pas la contribution du poteau AD dans le blocage du nœud A. Dans ce cas, le
facteur est
 Dans le cas contraire, on considère le poteau AD comme une autre poutre.
 Pour le cas intermédiaire,
: moment de blocage dans le poteau AD,
; = effort normale dans le poteau AD ; = charge critique Euler du
poteau AD.

48. Page 48 / 60
14.10. LONGUEUR EFFICACE D’UNE VOILE

49. Page 49 / 60

50. Page 50 / 60
14.11. Vérifier si l’effet 2nd
ordre local est négligeable
On peut admet que les effets du second ordre local peuvent être négligés si (5.8.3.1 (1))
Élancement est calculé basé sur la section grosse (sans prise en compte des
armatures).
Valeur recommandée de :
Si n’est pas connu, on peut prendre
Si n’est pas connu, on peut prendre
Si n’est pas connu, on peut prendre

51. Page 51 / 60
où
coefficient de fluage effectif ;
ratio mécanique d'armatures
est l'aire totale de la section des armatures longitudinales
n = NEd / (Acfcd) effort normal relatif
rapport des moments
sont les moments d'extrémité du premier ordre, .
Si les moments d'extrémité et provoquent des tractions sur une même face, il
convient de prendre positif (c.-à-d. C ≤ 1.7), sinon, de prendre négatif (c.-à-d. C > 1.7).
Dans les cas suivants, il convient de prendre = 1.0 (c.-à-d. C = 0.7) :
— éléments contreventés, pour lesquels les moments du premier ordre résultent uniquement
ou sont dus de manière prépondérante à des imperfections ou aux charges transversales
— éléments non contreventés en général

52. Page 52 / 60
14.12. Méthode de rigidité nominale :
Moment 2nd
ordre total d’un poteau isolé :
est la charge de flambement basée sur la rigidité nominale
est la longueur efficace d’un poteau isolé ;
est le moment du premier ordre, compte tenu de l'effet des imperfections et des
effets 2nd
ordre globaux (dans le cas où l’élément n’est pas soumis au même moment
en tête et en pied, on peut prendre le moment équivalent).
est un coefficient qui dépend de la distribution des moments du premier et du
second ordre, voir 5.8.7.3 (2)-(3)

53. Page 53 / 60
1. Dans le cas des éléments isolés de section constante soumis à un effort normal constant,
on peut normalement admettre une distribution sinusoïdale du moment du second ordre.
On a alors :
(Eq. 5.29)
où :
est un coefficient qui dépend de la distribution du moment du premier ordre
= 8 pour un moment du premier ordre constant,
= 9.6 pour une distribution parabolique et
= 12 pour une distribution triangulaire symétrique, etc.).

54. Page 54 / 60
2. Dans le cas d'éléments non soumis à une charge transversale, les moments d'extrémité du
premier ordre et , lorsqu'ils sont différents, peuvent être remplacés par un
moment du premier ordre équivalent , constant. Dans ce cas, il convient d'adopter
= 8.
3. Dans l’autre cas, = 1 constitue normalement une simplification raisonnable.
Il convient de prendre et de
même signe s'ils provoquent la
traction sur la même face et de signes
opposés dans le cas contraire.

55. Page 55 / 60
14.13. Méthode basée sur une courbure nominale
Le moment de calcul vaut
(Eq. 5.31)
(Eq. 5.33)
où
est le moment du premier ordre, compte tenu de l'effet des imperfections et des
effets 2nd
ordre globaux, voir le calcul dans la méthode de rigidité nominale.
est un coefficient dépendant de la distribution des courbures.
Pour une section constante, pour le cas de moment 1er
ordre constant et pour
autre cas.

56. Page 56 / 60
La courbure nominale :
(Eq. 5.34)
Où est la hauteur utile.
Si toutes les armatures ne sont pas
concentrées sur les faces opposées,
mais qu'une partie est distribuée
parallèlement au plan de flexion, est
défini par :
(Eq. 5.35)
où est le rayon de giration de la
section totale d'armatures.Plan de flexion
Armature distribué
parallèlement au plan de
flexion

57. Page 57 / 60
Facteur de correction dépendant de l'effort normal
(Eq. 5.36)
où
est la valeur de n correspondant au moment résistant maximal ; on peut supposer
que = 0.4
est l'aire totale de la section des armatures
est l'aire de la section droite du béton.
est l'effort normal agissant de calcul

58. Page 58 / 60
Coefficient tenant compte du fluage
(Eq. 5.37)
Où
est le coefficient de fluage effectif
est le coefficient d'élancement, basé sur la section non fissurée
(normalement calculé basé sur la section grosse sans prise en compte des armatures).

59. Page 59 / 60
14.14. CALCULER LE MOMENT D’UN POTEAU ISOLÉ
= Moment 1er
ordre (vent, imperfection sur le contreventement, charge verticale, …)
+ Moment dû à l’imperfection local du poteau isolé.
 Moment dû à l’imperfection local du poteau isolé

60. Page 60 / 60
Avec
(Eq. 5.2)
Dans le cas des voiles et des poteaux isolés dans des structures
contreventées, il est toujours possible, pour simplifier, d'adopter
, ce qui correspond à = 1.
Poteau isolé contreventé :
(Eq. 5.3a)
Poteau isolé non-contreventé :
(Eq. 5.3b)
(Eq. 5.1)