Le document présente un projet de laboratoire à l'Institut de Technologie du Cambodge, axé sur le calcul des efforts internes d'une poutre. Trois cas différents sont analysés à l'aide d'un script MATLAB, permettant de déterminer les moments d'inertie, les réactions d'appuis, les efforts tranchants et les moments fléchissants, ainsi que les contraintes en flexion. Les résultats sont enregistrés dans des fichiers texte pour chaque cas, et des vérifications des contraintes admissibles sont effectuées.

1. INSTITUTE OF TECHNOLOGY OF CAMBODIA
---DEPARTMENT OF CIVIL ENGINEERING--
LECTURER: Dr. Keang Sé POUV
STUDENTS: 1. KAM Channraksmee (e20140229)
2. KECH Sengthai (e20140244)
3. KEN Koemhong (e20140247)
4. KHEN Chanthorn (e20140267)
CLASS: I3 -GCI-A
--Scholar Year--
--2016 – 2017--
(2)

2. Institut de Technologie du Cambodge TP2 TP Matlab
1Groupe 08 2016 - 2017
TP2 Mini-projet :
SOLUTION
1. Pour le premier cas a=20cm, b=40cm, L=8m, L1=2m, sigma_a=28 MPa, P=40 kN
SCRIPT
function [Iz, R1, R2, T, M, sigma_x] = TP2( a, b, L, L1, sigma_a, P )
%input a et b must be in meter
disp('* Moment inertie Iz')
Iz=a*b^3/12;
fprintf(' Iz = %.4f m4 rn', Iz);
disp('* Reaction dappuis 1 et 2')
R1=(P*(L-L1))/L;
R2=(P*L1)/L;
fprintf(' R1 = %.f kN, et R2 = %.f kN rn', R1,R2);
disp('* Effort Tranchant T [kN] et Moment fléchissant M [kN.m]')
disp('- Pour 0<=x<=L')
for x=0:L;
if x<=L1
T=R1;
M=R1*x;
fprintf(' Pour x = %.0f m, T = %.0f kN et M = %.0f kN.m rn',x,T,M)
else
T=-R2;
M=R2*(L-x);
fprintf(' Pour x = %.0f m, T = %.0f kN et M=%.0f kN.m rn',x,T,M)
end
end
disp ('* Contrainte en flexion [MPa] en position du moment maximal variant aux valeurs de
y')
y=-b/2:0.1:b/2;
M_max=R1*L1;
sigma_x=(10^-3).*y.*M_max.*(1/Iz);
fprintf(' Pour y=%.2f m rn',y)
disp('+ Donc, les valeurs sigma_x correspondant')
fprintf(' sigma_x = %.3f MPa rn',sigma_x)
sigma_x_max=max(sigma_x);
fprintf(' Et sigma_x_max =%.4f MParn',sigma_x_max);
if sigma_x_max<=sigma_a
disp('(Contrainte maximale <= contrainte admisible, VERIFIE!)')
else
disp('(Contrainte maximale > contrainte admisible, NON VERIFIE!)')
end
x=linspace(0,L,1000);
for i=1:1000
if x(i)<=L1;
Effort internes d’une poutre sur appuis simple

3. Institut de Technologie du Cambodge TP2 TP Matlab
2Groupe 08 2016 - 2017
T(i)=R1;
M(i)=R1*x(i);
else
T(i)=-R2;
M(i)=R2*(L-x(i));
end
end
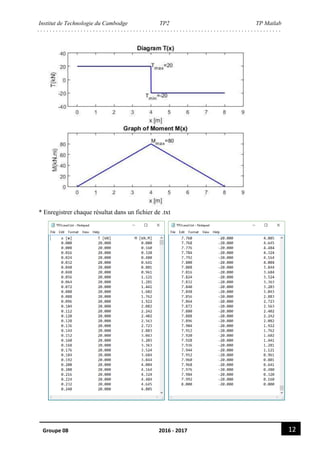
figure
subplot (2,1,1)
plot (x,T,'b','linewidth',1.5)
axis ([-0.5,9,-R2-20,R1+20])
title ('Diagram T')
xlabel ('x [m]')
ylabel ('T(kN)')
text(L1,R1+0.5,'T_m_a_x=30')
text(L1-0.3,-R2-5,'T_m_i_n=-10')
subplot (2,1,2)
plot (x,M,'b','linewidth',1.5)
axis ([-0.5,9,min(M),max(M)+20])
title ('Graph of Moment M')
xlabel ('x [m]')
ylabel ('M(kN.m)')
text(L1,max(M)+5,'M_m_a_x')
% Enregistrer le résultat au ficher .txt
% Case 1
disp('* Enregistrer chaque résultat dans un ficher de .txt')
A=[x; T; M];
fileid=fopen('TP2case1.txt','w');
fprintf(fileid,' x [m] T [kN] M [kN.M] rn');
fprintf(fileid,' %.3f %.3f %.3frn',A);
fclose(fileid);
end
LE COMMAND WINDOW (cas 1)
>> TP2(0.2,0.4,8,2,28,40)
* Moment inertie Iz
Iz = 0.0011 m4
* Reaction dappuis 1 et 2
R1 = 30 kN, et R2 = 10 kN
* Effort Tranchant T [kN] et Moment fléchissant M [kN.m]
- Pour 0<=x<=L
Pour x = 0 m, T = 30 kN et M = 0 kN.m
Pour x = 1 m, T = 30 kN et M = 30 kN.m
Pour x = 2 m, T = 30 kN et M = 60 kN.m

4. Institut de Technologie du Cambodge TP2 TP Matlab
3Groupe 08 2016 - 2017
Pour x = 3 m, T = -10 kN et M=50 kN.m
Pour x = 4 m, T = -10 kN et M=40 kN.m
Pour x = 5 m, T = -10 kN et M=30 kN.m
Pour x = 6 m, T = -10 kN et M=20 kN.m
Pour x = 7 m, T = -10 kN et M=10 kN.m
Pour x = 8 m, T = -10 kN et M=0 kN.m
* Contrainte en flexion [MPa] en position du moment maximal variant aux valeurs de y
Pour y=-0.20 m
Pour y=-0.10 m
Pour y=0.00 m
Pour y=0.10 m
Pour y=0.20 m
+ Donc, les valeurs sigma_x correspondant
sigma_x = -11.250 MPa
sigma_x = -5.625 MPa
sigma_x = 0.000 MPa
sigma_x = 5.625 MPa
sigma_x = 11.250 MPa
Et sigma_x_max =11.2500 MPa
(Contrainte maximale <= contrainte admissible, VERIFIE!)

5. Institut de Technologie du Cambodge TP2 TP Matlab
4Groupe 08 2016 - 2017
* Enregistrer chaque résultat dans un ficher de .txt

6. Institut de Technologie du Cambodge TP2 TP Matlab
5Groupe 08 2016 - 2017
2. Pour le deuxième cas a=20cm, b=40cm, L=8m, L1=3m, sigma_a=28 MPa, P=28 kN
SCRIPT :
>>
function [Iz, R1, R2, T, M, sigma_x] = TP2( a, b, L, L1, sigma_a, P )
%input a et b must be in meter
disp('* Moment inertie Iz')
Iz=a*b^3/12;
fprintf(' Iz = %.4f m4 rn', Iz);
disp('* Reaction dappuis 1 et 2')
R1=(P*(L-L1))/L;
R2=(P*L1)/L;
fprintf(' R1 = %.f kN, et R2 = %.f kN rn', R1,R2);
disp('* Effort Tranchant T [kN] et Moment fléchissant M [kN.m]')
disp('- Pour 0<=x<=L')
for x=0:L;
if x<=L1
T=R1;
M=R1*x;
fprintf(' Pour x = %.0f m, T = %.0f kN et M = %.0f kN.m rn',x,T,M)
else
T=-R2;
M=R2*(L-x);
fprintf(' Pour x = %.0f m, T = %.0f kN et M=%.0f kN.m rn',x,T,M)
end
end
disp ('* Contrainte en flexion [MPa] en position du moment maximal variant aux valeurs de
y')
y=-b/2:0.1:b/2;
M_max=R1*L1;
sigma_x=(10^-3).*y.*M_max.*(1/Iz);
fprintf(' Pour y=%.2f m rn',y)
disp('+ Donc, les valeurs sigma_x correspondant')
fprintf(' sigma_x = %.3f MPa rn',sigma_x)
sigma_x_max=max(sigma_x);
fprintf(' Et sigma_x_max =%.4f MParn',sigma_x_max);
if sigma_x_max<=sigma_a
disp('(Contrainte maximale <= contrainte admisible, VERIFIE!)')
else
disp('(Contrainte maximale > contrainte admisible, NON VERIFIE!)')
end
x=linspace(0,L,1000);
for i=1:1000
if x(i)<=L1;
T(i)=R1;
M(i)=R1*x(i);
else
T(i)=-R2;

7. Institut de Technologie du Cambodge TP2 TP Matlab
6Groupe 08 2016 - 2017
M(i)=R2*(L-x(i));
end
end
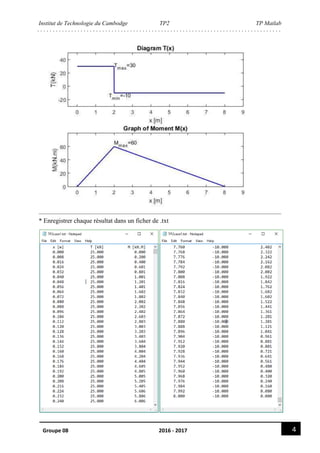
figure
subplot (2,1,1)
plot (x,T,'b','linewidth',1.5)
axis ([-0.5,9,-R2-20,R1+20])
title ('Diagram T')
xlabel ('x [m]')
ylabel ('T(kN)')
text(L1,R1+0.5,'T_m_a_x=25')
text(L1-0.3,-R2-5,'T_m_i_n=-15')
subplot (2,1,2)
plot (x,M,'b','linewidth',1.5)
axis ([-0.5,9,min(M),max(M)+20])
title ('Graph of Moment M')
xlabel ('x [m]')
ylabel ('M(kN.m)')
text(L1,max(M)+5,'M_m_a_x=75')
% Enregistrer le résultat au ficher .txt
% Case 1
disp('* Enregistrer chaque résultat dans un ficher de .txt')
A=[x; T; M];
fileid=fopen('TP2case2.txt','w');
fprintf(fileid,' x [m] T [kN] M [kN.M] rn');
fprintf(fileid,' %.3f %.3f %.3frn',A);
fclose(fileid);
end
COMMAND WINDOW (cas 2)
>> TP2(0.2,0.4,8,3,28,40)
* Moment inertie Iz
Iz = 0.0011 m4
* Reaction dappuis 1 et 2
R1 = 25 kN, et R2 = 15 kN
* Effort Tranchant T [kN] et Moment fléchissant M [kN.m]
- Pour 0<=x<=L
Pour x = 0 m, T = 25 kN et M = 0 kN.m
Pour x = 1 m, T = 25 kN et M = 25 kN.m
Pour x = 2 m, T = 25 kN et M = 50 kN.m
Pour x = 3 m, T = 25 kN et M = 75 kN.m

8. Institut de Technologie du Cambodge TP2 TP Matlab
7Groupe 08 2016 - 2017
Pour x = 4 m, T = -15 kN et M=60 kN.m
Pour x = 5 m, T = -15 kN et M=45 kN.m
Pour x = 6 m, T = -15 kN et M=30 kN.m
Pour x = 7 m, T = -15 kN et M=15 kN.m
Pour x = 8 m, T = -15 kN et M=0 kN.m
* Contrainte en flexion [MPa] en position du moment maximal variant aux valeurs de y
Pour y=-0.20 m
Pour y=-0.10 m
Pour y=0.00 m
Pour y=0.10 m
Pour y=0.20 m
+ Donc, les valeurs sigma_x correspondant
sigma_x = -14.062 MPa
sigma_x = -7.031 MPa
sigma_x = 0.000 MPa
sigma_x = 7.031 MPa
sigma_x = 14.062 MPa
Et sigma_x_max =14.0625 MPa
(Contrainte maximale <= contrainte admissible, VERIFIE!)

9. Institut de Technologie du Cambodge TP2 TP Matlab
8Groupe 08 2016 - 2017
* Enregistrer chaque résultat dans un fichier de .txt

10. Institut de Technologie du Cambodge TP2 TP Matlab
9Groupe 08 2016 - 2017
3. Pour le troisième cas a=20cm, b=0.4, L=8m, L1=4m, sigma_a=28 MPa, P=40 kN
SCRIPT
>>
function [Iz, R1, R2, T, M, sigma_x] = TP2Thai( a, b, L, L1, sigma_a, P )
%input a et b must be in meter
disp('* Moment inertie Iz')
Iz=a*b^3/12;
fprintf(' Iz = %.4f m4 rn', Iz);
disp('* Reaction dappuis 1 et 2')
R1=(P*(L-L1))/L;
R2=(P*L1)/L;
fprintf(' R1 = %.f kN, et R2 = %.f kN rn', R1,R2);
disp('* Effort Tranchant T [kN] et Moment fléchissant M [kN.m]')
disp('- Pour 0<=x<=L')
for x=0:L;
if x<=L1
T=R1;
M=R1*x;
fprintf(' Pour x = %.0f m, T = %.0f kN et M = %.0f kN.m rn',x,T,M)
else
T=-R2;
M=R2*(L-x);
fprintf(' Pour x = %.0f m, T = %.0f kN et M=%.0f kN.m rn',x,T,M)
end
end
disp ('* Contrainte en flexion [MPa] en position du moment maximal variant aux valeurs de
y')
y=-b/2:0.1:b/2;
M_max=R1*L1;
sigma_x=(10^-3).*y.*M_max.*(1/Iz);
fprintf(' Pour y=%.2f m rn',y)
disp('+ Donc, les valeurs sigma_x correspondant')
fprintf(' sigma_x = %.3f MPa rn',sigma_x)
sigma_x_max=max(sigma_x);
fprintf(' Et sigma_x_max =%.4f MParn',sigma_x_max);
if sigma_x_max<=sigma_a
disp('(Contrainte maximale <= contrainte admisible, VERIFIE!)')
else
disp('(Contrainte maximale > contrainte admisible, NON VERIFIE!)')
end

11. Institut de Technologie du Cambodge TP2 TP Matlab
10Groupe 08 2016 - 2017
x=linspace(0,L,1000);
for i=1:1000
if x(i)<=L1;
T(i)=R1;
M(i)=R1*x(i);
else
T(i)=-R2;
M(i)=R2*(L-x(i));
end
end
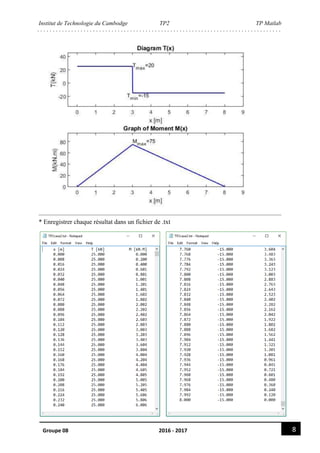
figure
subplot (2,1,1)
plot (x,T,'b','linewidth',1.5)
axis ([-0.5,9,-R2-20,R1+20])
title ('Diagram T')
xlabel ('x [m]')
ylabel ('T(kN)')
text(L1,R1+0.5,'T_m_a_x=20')
text(L1-0.3,-R2-5,'T_m_i_n=-20')
subplot (2,1,2)
plot (x,M,'b','linewidth',1.5)
axis ([-0.5,9,min(M),max(M)+20])
title ('Graph of Moment M')
xlabel ('x [m]')
ylabel ('M(kN.m)')
text(L1,max(M)+5,'M_m_a_x=80')
% Enregistrer le résultat au ficher .txt
% Case 1
disp('* Enregistrer chaque résultat dans un ficher de .txt')
A=[x; T; M];
fileid=fopen('TP2case3.txt','w');
fprintf(fileid,' x [m] T [kN] M [kN.M] rn');
fprintf(fileid,' %.3f %.3f %.3frn',A);
fclose(fileid);
end
COMMAND WINDOW (cas 3)
>> TP2(0.2,0.4,8,4,28,40)
* Moment inertie Iz
Iz = 0.0011 m4
* Reaction dappuis 1 et 2
R1 = 20 kN, et R2 = 20 kN
* Effort Tranchant T [kN] et Moment fléchissant M [kN.m]
- Pour 0<=x<=L
Pour x = 0 m, T = 20 kN et M = 0 kN.m
Pour x = 1 m, T = 20 kN et M = 20 kN.m

12. Institut de Technologie du Cambodge TP2 TP Matlab
11Groupe 08 2016 - 2017
Pour x = 2 m, T = 20 kN et M = 40 kN.m
Pour x = 3 m, T = 20 kN et M = 60 kN.m
Pour x = 4 m, T = 20 kN et M = 80 kN.m
Pour x = 5 m, T = -20 kN et M=60 kN.m
Pour x = 6 m, T = -20 kN et M=40 kN.m
Pour x = 7 m, T = -20 kN et M=20 kN.m
Pour x = 8 m, T = -20 kN et M=0 kN.m
* Contrainte en flexion [MPa] en position du moment maximal variant aux valeurs de y
Pour y=-0.20 m
Pour y=-0.10 m
Pour y=0.00 m
Pour y=0.10 m
Pour y=0.20 m
+ Donc, les valeurs sigma_x correspondant
sigma_x = -15.000 MPa
sigma_x = -7.500 MPa
sigma_x = 0.000 MPa
sigma_x = 7.500 MPa
sigma_x = 15.000 MPa
Et sigma_x_max =15.0000 MPa
(Contrainte maximale <= contrainte admisible, VERIFIE!)

13. Institut de Technologie du Cambodge TP2 TP Matlab
12Groupe 08 2016 - 2017
* Enregistrer chaque résultat dans un fichier de .txt

14. Institut de Technologie du Cambodge TP2 TP Matlab
13Groupe 08 2016 - 2017
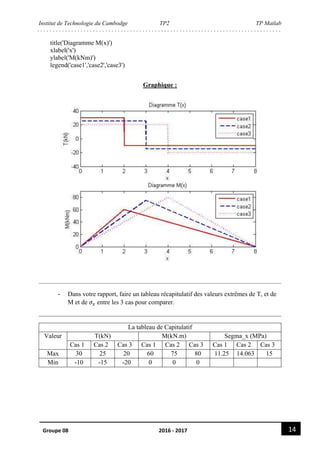
En fin, on souhaite comparer et analyser les résultats des 3 cas d’études :
- Tracez les diagrammes 𝑇(𝑥) et 𝑀(𝑥) pour les 3 cas en utilisant uniquement les
fichiers .txt enregistrés auparavant (Conseils : mettez les 3 courbes de même
paramètre sur même graphique, puis alignez verticalement les 2 graphiques sur la
même figure.)
SCRIPT:
%%
%case1
file1=fopen('TP2case1.txt','r');
format='%f %f %f';
A=fscanf(file1,format);
B=reshape(A,3,1000);
x1=B(1,:);
T1=B(2,:);
M1=B(3,:);
%%
%case2
file2=fopen('TP2case2.txt','r');
format='%f %f %f';
C=fscanf(file2,format);
D=reshape(C,3,1000);
x2=D(1,:);
T2=D(2,:);
M2=D(3,:);
%%
%Case3
file3=fopen('TP2case3.txt','r');
format='%f %f %f';
E=fscanf(file3,format);
F=reshape(E,3,1000);
x3=F(1,:);
T3=F(2,:);
M3=F(3,:);
%%
figure
subplot(2,1,1)
plot(x1,T1,'-r',x2,T2,'--b',x3,T3,':m','linewidth',2)
axis([0,8,-40,40])
title('Diagramme T(x)')
xlabel('x')
ylabel('T(kN)')
legend('case1','case2','case3')
subplot(2,1,2)
plot(x1,M1,'-r',x2,M2,'--b',x3,M3,':m','linewidth',2)
axis([0,8,0,90])

15. Institut de Technologie du Cambodge TP2 TP Matlab
14Groupe 08 2016 - 2017
title('Diagramme M(x)')
xlabel('x')
ylabel('M(kNm)')
legend('case1','case2','case3')
Graphique :
- Dans votre rapport, faire un tableau récapitulatif des valeurs extrêmes de T, et de
M et de 𝜎𝑥 entre les 3 cas pour comparer.
La tableau de Capitulatif
Valeur T(kN) M(kN.m) Segma_x (MPa)
Cas 1 Cas 2 Cas 3 Cas 1 Cas 2 Cas 3 Cas 1 Cas 2 Cas 3
Max 30 25 20 60 75 80 11.25 14.063 15
Min -10 -15 -20 0 0 0