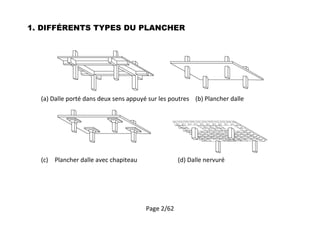
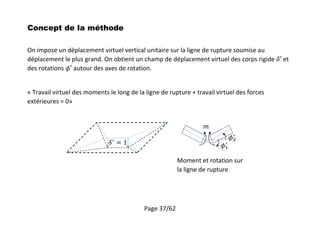
Le document traite des différents types de dalles portées sur poutres et de leur estimation d'épaisseur, notamment pour les bâtiments et parkings. Une méthode d'analyse structurale est présentée, comprenant des techniques telles que l'analyse linéaire élastique et la méthode de rupture de Johansen, ainsi que des règles pour le dimensionnement des armatures. Il couvre également divers calculs liés à la résistance des dalles et à l'armature des pièces en béton armé.







![Page 24/62
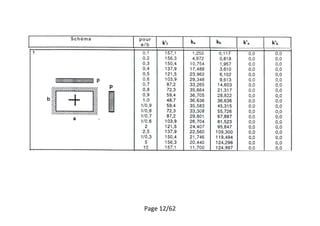
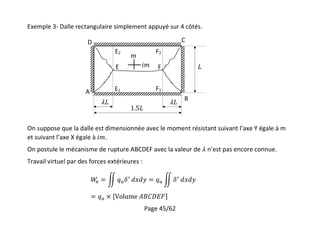
Exemple :
SOLUTION
Poids propre de la dalle pp = (0.15 m) *(25 kN/m3
) = 3.75 kN/m2
;
Charge répartie à l’ELU pu = 1.35 (3.75+4) + 1.5 (2) = 13.5 kN/m2
;
o Côté AB et AD est considérés comme appui simple
o Côté BC et CD est considérés comme appui encastré
6 m6 m
4 m
4 m
Epaisseur de la dalle = 15 cm
Surcharge permanente = 4 kN/m2
Surcharge variable = 2 kN/m2
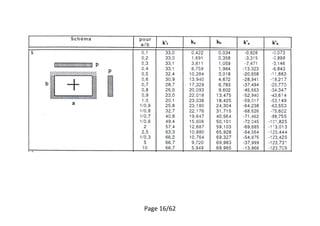
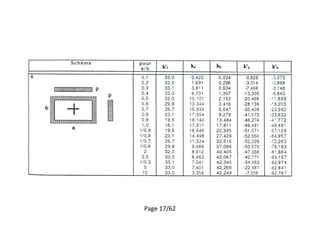
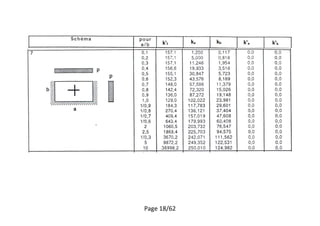
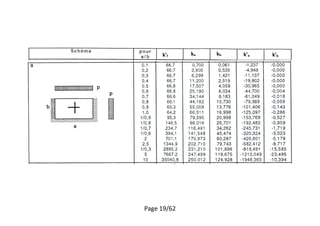
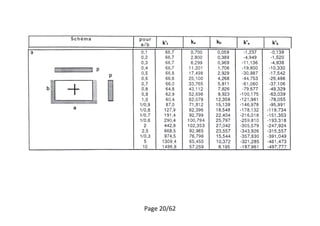
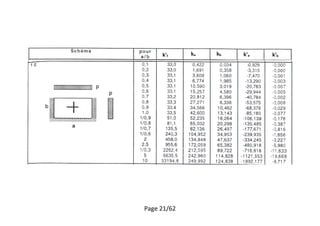
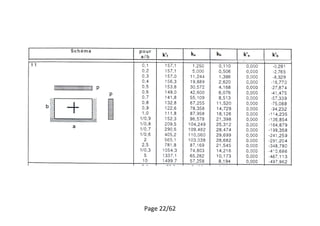
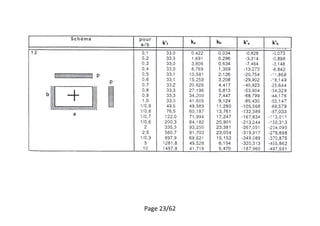
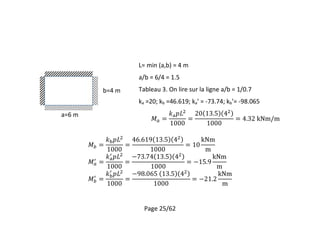
Calculer le moment pour le panel 1
[1]
A B
CD](https://image.slidesharecdn.com/12-plancher-180707142840/85/12-plancher-Eurocode-2-24-320.jpg)
![Page 26/62
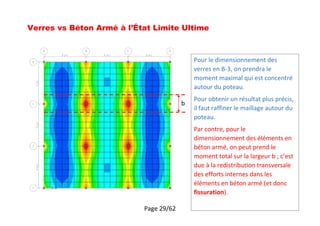
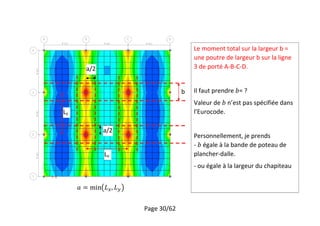
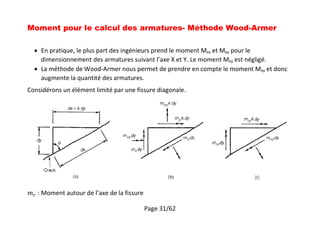
4.32
15.9
21.2
10
Moment [kNm/m]](https://image.slidesharecdn.com/12-plancher-180707142840/85/12-plancher-Eurocode-2-26-320.jpg)


















![Page 53/62
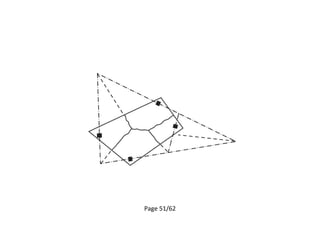
4.2 Armatures dans une dalle pleine appuyée sur les poutres
Dalle portée dans une direction/ One-way slab- Armatures supérieures
Armature principale
Armature secondaire/
armature de répartition
Cet armature n’est pas
nécessaire s’il n’y a pas de
moment transversal
[9.3.1.1(2)]
Armature secondaire
Armature principale
A
A
SECTION A-A
NOTE : Position des armatures secondaires par rapport aux armatures principales ?
Maximiser le pour les armatures principales](https://image.slidesharecdn.com/12-plancher-180707142840/85/12-plancher-Eurocode-2-53-320.jpg)
![Page 55/62
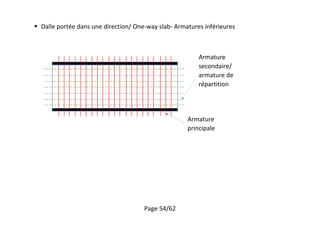
Dalle portée dans deux directions/ Two-way slab- Armatures supérieures
Règle de couture : décalage du diagramme de moment . [9.3.1.1.(4)]
Armature
principale
Armature
secondaire/
armature de
répartition](https://image.slidesharecdn.com/12-plancher-180707142840/85/12-plancher-Eurocode-2-55-320.jpg)
![Page 57/62
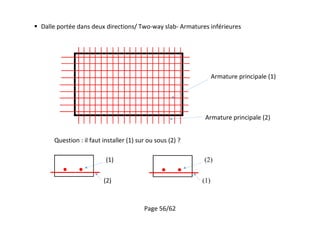
4.3 Armature principale minimum
Valeur recommandée, [UK], [NF] : [9.2.1.1(1)]
,
4.4 Armature principale maximal
Valeur recommandée, [UK], [NF]: [9.2.1.1(3)]
,
Ou si le bétonnage est possible, norme [NF] permet:
,](https://image.slidesharecdn.com/12-plancher-180707142840/85/12-plancher-Eurocode-2-57-320.jpg)
![Page 58/62
4.5 Armature secondaire
Pour la dalle portée dans une direction, armature secondaire 20% Armature principale.
Au voisinage des appuis, des armatures transversales aux barres principales supérieures
ne sont pas nécessaires lorsqu'il n'existe aucun moment fléchissant transversal.
[9.3.1.1(2)]
4.6 Espacement Maximum des Bars
Valeurs recommandées [9.3.1.1(3)]
Armatures principales : , où h est l’épaisseur totale de la dalle ;
Armatures secondaires : , .
Dans les zones sollicitées par des charges concentrées ou dans les zones de moment maximal,
ces dispositions deviennent respectivement :
— pour les armatures principales, ,
— pour les armatures secondaires, ,](https://image.slidesharecdn.com/12-plancher-180707142840/85/12-plancher-Eurocode-2-58-320.jpg)
![Page 59/62
4.7 Armatures de bords libres
Le long du bord libre (non appuyé) d'une dalle, il convient normalement de prévoir des
armatures longitudinales et transversales, généralement disposées comme représenté sur
la Figure 9.8. [9.3.1.4(1)]
Eurocode n’a pas précisé la quantité des armatures à utiliser.](https://image.slidesharecdn.com/12-plancher-180707142840/85/12-plancher-Eurocode-2-59-320.jpg)
![Page 60/62
4.8 Armatures au voisinage des appuis
(1) Dans les dalles sur appuis simples, il convient de prolonger jusqu'à l'appui la moitié des
armatures calculées en travée, et de les y ancrer conformément à 8.4.4.
At0.5At
en [8.4.4]](https://image.slidesharecdn.com/12-plancher-180707142840/85/12-plancher-Eurocode-2-60-320.jpg)
![Page 62/62
5. Armatures d’effort tranchant
Lorsque des armatures d’effort tranchant sont prévues dans une dalle, il convient que
l’épaisseur de la dalle soit au moins égale à 200 mm. [9.3.2(1)]
L'espacement longitudinal maximal des cadres, étriers ou épingles est donné par :
où est l’inclinaison des armatures d’effort tranchant. [9.3.2(4)]
Il convient de limiter à 1.5d l'espacement transversal maximal des armatures d’effort
tranchant. [9.3.2(5)]](https://image.slidesharecdn.com/12-plancher-180707142840/85/12-plancher-Eurocode-2-62-320.jpg)