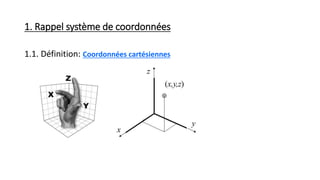
Le document présente le contenu d'un cours sur la vibration mécanique au sein de l'Institut de Technologie du Cambodge, abordant des concepts fondamentaux tels que les systèmes de coordonnées, la masse, le centre de masse et le moment d'inertie. Il comprend également des discussions sur la quantité de mouvement, le moment cinétique, et le référentiel du centre de masse. Enfin, des théorèmes comme celui de Huygens-Schteiner et du moment cinétique d'un solide en rotation sont également traités.

1. Institute de Technologie du Cambodge
Formation de Physique pour d’ingénieur
Course: Vibration Mécanique
Date: 29 août -03 septembre 2016
Salle: F-106

2. 1. Rappel système de coordonnées
1.1. Définition: Coordonnées cartésiennes

3. 1. Rappel système de coordonnées
1.1. Définition: Coordonnées cylindrique

4. 1. Rappel système de coordonnées
1.1. Définition: Coordonnées sphérique

5. 1. Rappel système de coordonnées
1.2. Vecteur unitaire
𝒖 𝒙
𝒖 𝒚
𝒖 𝒛
𝒖 𝝆
𝒖 𝝓
𝒖 𝒛
𝒖 𝝓
𝒖 𝜽
𝒖 𝒓

6. 1. Rappel système de coordonnées
1.3. Elémentaire de déplacement, surface et volume
x y zdOP dxu dyu dzu  
uuur r r r
. . .ds dx dy dx dz dy dz  
d dxdydz 
zdOP d u d u dzu     
uuur r r r
. . .ds d d d dz d dz       
. .d d d dz   

7. 1. Rappel système de coordonnées
1.3. Elémentaire de déplacement, surface et volume
sinrdOP dru rd u r d u     
uuur r r r
2
sin . . .d r dr d d   
2
. sin . . sin .ds rdr d r dr d r d d       

8. 1. Rappel système de coordonnées
1.3. Elémentaire de déplacement, surface et volume
sinrdOP dru rd u r d u     
uuur r r r
2
sin . . .d r dr d d   
2
. sin . . sin .ds rdr d r dr d r d d       

9. 2. Éléments cinétiques des système matériels
2.1 Masse d'un système matériel
• Distribution discontinue de masse: 𝑚 = ∑𝑚𝑖
• Distribution continue de masse: 𝑚 = ∫ 𝑑𝑚
i. Distribution volumique de masse: 𝑚 = 𝜌 𝐴 𝑑𝜏
ii. Distribution surfacique de masse: 𝑚 = 𝜎 𝐴 𝑑𝑠
iii. Distribution linéique de masse: 𝑚 = ∫ 𝜆 𝐴 𝑑𝑙
2.2 Centre de masse d'un système matériel
• Définition de centre de masse:
i. Distribution discontinue de masse: 𝑂𝐶 =
∑𝑚 𝑖 𝑂𝐶 𝑖
∑𝑚 𝑖
𝑜𝑢 ∑𝑚𝑖 𝐶𝐶𝑖 = 0
ii. Distribution continue de masse : 𝑂𝐶 =
∫ 𝑂𝐴𝑑𝑚
∫ 𝑑𝑚
𝑜𝑢 ∫ 𝐶𝐴𝑑𝑚 = 0

10. 3. Moment d’inertie
3.1 Définition
• Moment d’inertie de masse 𝑚 par rapport à l’axe Δ: 𝐼 = 𝑚. 𝑟2
• Moment d’inertie d’un système discontinue de masse , par rapport à
l’axe Δ: 𝐼 = ∑𝑚𝑖. 𝑟𝑖
2
• Moment d’inertie d’un système continue de masse , par rapport à
l’axe Δ: 𝐼 = ∫ 𝑟2 𝑑𝑚
𝐴(𝑑𝑚)
𝑟

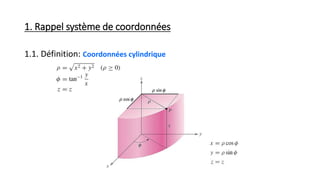
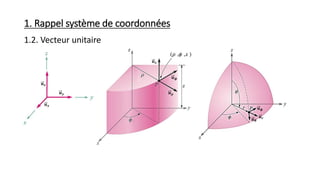
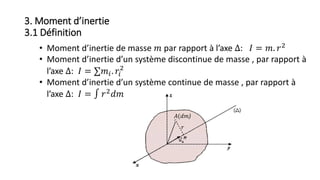
11. 3. Moment d’inertie
3.2 Opérateur d’inertie
 
2
2
2
2 2 2
2 2 2
0A
; OA ; ( ) ( ) ( )
2 2 2
e [c:
.
]v
i
xx yy zz xy xz yz O
xx xy xz
xy yy yz
xz yz
I r dm u OA dm
x
u y u OA z y z x x y
z
I I I I I I I u I u
I I I
I I I I
I I

      

     
 
 
  
  
   
   
           
   
   
       
 
  
 
 
uuurr
uuur uuurr r
r r
:
zzI

 
 
 
 
 
𝐴(𝑑𝑚)
)
0Nous obtenons: .[ ]I u I u  
r r

12. 3. Moment d’inertie
3.2 Opérateur d’inertie
𝑟
0
2 2
2 2
[ ] : ' '
( ) : le moment d'inertie par rapport à axe (Ox)
( ) : le moment d'in
Avec
ertie p
:
ar rapport
xx xy xz
xy yy yz
xz yz zz
xx
yy
I I I
I I I I Matriced inertie ou opérateur d inertie
I I I
I y z dm
I x z dm

  
 
   
   
 
 



2 2
à axe (Oy)
= ( ) : le moment d'inertie par rapport à (Oz)
, , : le produit d'inertie
zz
xy xz yz
I x y dm
I xydm I xzdm I yzdm

  

  

13. 13
La matrice d’inertie dépend de l’origrne des axes du triedre choisi. Etudions
l’influence d’une translation des axes de triedre initial Oxyz et le nouveau
triedre O’x’y’z’ . En désignant par a, b, c les cordonnées de O’
3. Moment d’inertie
3.3 Théorème de Huygens-Schteiner
' ' '
' ' '
' ' '
2 2
' '
On pose : ; ' et OO' OO' '
.( ) 2 ' 2xx x x
x x a x x ax a
OA y O A y b OA O A y b y y b
z cz z c z z c
I I M b c b y dm c
         
       
                 
                    
    


uuur uuuur uuuur uuur uuuur uuuur
' '
2 2
' ' ' '
2 2
' ' ' '
' . ' '
.( ) 2 ' 2 ' et . ' '
.( ) 2 ' 2 ' . ' '
xy x y
yy y y xz x z
zz z z yz y z
z dm I I M ab a y dm b x dm
I I M a c a x dm c z dm I I M ac a z dm c x dm
I I M a b a x dm b y dm I I M bc b z dm c y dm
     
 
 
         
 
         
 
  
   
   

14. 14
2 2
' ' ' '
2 2
' ' ' '
2 2
' '
' 0
Si ' ' , d'autre part: 0 ' 0
' 0
.( ) .
.( ) et .
.( )
C
C
C
xx x x xy x y C C
yy y y xz x z
zz z z
x dm
x a
O C OO OC y b CAdm y dm
z c
z dm
I I M b c I I M x y
I I M a c I I M x
I I M a b
 
 
 
        
   

     

     

  

 

uuuuur uuur uuur r
' ' .
C C
yz y z C C
z
I I M y z



  
3. Moment d’inertie
3.3 Théorème de Huygens-Schteiner

15. 15
Le moment d'inertie d'un solide par rapport à une droite est
égal à la somme du moment d'inertie par rapport à cette
droite de la masse du solide concentrée au centre de masse
C (Md2)et du moment d'inertie du solide par rapport à la
droite parallèle passant par C (IC).
2
CI I md  
2 2
Par exemple: .( )xx Cx C CI I m y z  
3. Moment d’inertie
3.3 Théorème de Huygens-Schteiner

16. 16
4. Quantité de mouvement
• Pour un point matériel: la quantité mouvement du point A par
rapport à référentiel  s’écrit:
/AP m 
r r
v
• Pour un système matériel: la quantité mouvement d’un système
par rapport à référentiel  s’écrit :
i i
i
P m 
r r
v
( ) Am
P dm 
r r
v
i. Système de masse discontinue
ii. Système de masse continue
( ) ( ) ( )
( )A m Cm m
dOA d d
dm P dm OAdm mOC m
dt dt d
P
t
       
uuur
uuur uuurrr r r
v v

17. 17
5. Moment cinétique
• Pour un point matériel: le moment cinétique en point O de 
du point A s’écrit:
/O AOA m  
uuur rr
v
• Pour un système matériel: le moment cinétique en point O de
 d’un système matériel s’écrit :
O i i i
i
OA m  
uuur rr
v
( )O Am
OA dm  
uuur rr
vii. Système de masse continue
i. Système de masse discontinue

18. 18
• Si O’ est un autre point fixe de , on a ​une relation simple entre
les moments cinétiques en O et O’
 ( ) ( )
( ) ( )
' '( )
' '
' '
'
' '
'
' '
v v
v v
v
v
O m m
m m
O
O C
O
O O
m
OA dm OO O A dm
OO dm O A dm
OO dm OO P
OO P OO M
 
 
     
   
  


    
 
 
 

uuur uuuur uuuurr rr
uuuur uuuurr r
uuuur uuuur
uuuur uuuurr rr r
r
r
rr r
Si O’  C
O C COC M   
uuur rr r
v
5. Moment cinétique

19. 19
6.1 Définition: Le référentiel du centre de masse associé à * est
le référentiel en translation par rapport à  et tel que:
*
*
*
*
*
/
* *
0
0 0
A
S
RR
dCA d
P P v dm dm CAdm
dt dt
P

   
           
  
  
uuur
r uuur rr r
r rr r
CComme v
Le centre de masse C est fixe dans *
6. Référentiel du centre de masse
6.2 Quantité dans * :

20. 20
*
*
* * *
*
*
*
( ) ( ( ))
( )
( )
( ) ( ( ))
( )
,
C A A C
A C
C A
C A A C
A C
CA dm CA dm
CA dm CAdm
CA dm
CA dm CA dm
CA dm CAdm
car CA




    
  
  
    
  

 
 

 
 
uuur uuurr r rr
uuur uuurr r
uuur rr
uuur uuurr r rr
uuur uuurr r
r
C
Dans : v v +v
v v
Dans : v
Dans : v v +v
v v
* *
0
C A
dm
CA dm 

 


uuur r
uuur rr r
C (m)
Donc: = v
6. Référentiel du centre de masse
6.3 Moment cinétique dans *

21. 21
*
/
O A
A A
OA dm
OA OC CA


 
 

uuur rr
uuur uuur uuurr r r
(m)
C
v
Avec: v = v + v et
 
*
(
* *
( ( ( (
*
*
( ) ( )
: ,
O A Cm
A C Am m m m
C
O C
OC CA dm
OC dm OC dm CA dm CAdm
OC m
Donc OC m car


   
   
       
  
   

   
uuur uuur r rr
uuur uuur uuur uuurr r r r
uuur r r
uuur rr r r r
)
C) ) ) )
C
C C C
v v
v v v v
v
v
6. Référentiel du centre de masse
6.4 Théorème de Koenig

22. 22
7. Moment cinétique d’un solide en rotation
( )
(m)
vO OA dm  
uuur rr
Pour mouvement rotation:
 
 C C
O O
I
I
 
 


rr
rr
v OA 
uuurr r

23. 8. Torseur dynamique
• Torseur dynamique est défini par :
 
( )
( )
:
:
)
Cv
O v
m
OA
 
 
 
 


r r r
uuurr r
D ad a résultante dynamique (quantité d'accélération)
N a d momnent de la résultante dynamique
(moment de la quantité d'accélération
23
 O
O
D
N

 

ur
uurD

24. 9. Torseur cinétique
• Torseur cinétique est défini par :
 
 
( )
( )
:Cv
O v
O
O
P
m
OA
 


 

 








r r r
uuur rr
ur
ur
Ap v d v Résultante cinétique
v d : Moment cinétique
P
24

25. 10. Relation entre torseur cinétique et torseur dynamique
( ) ( )
( (C O
C A Av v
m m OA OA
t t t t

       
r r r uuur uuurr rrdv ddP d
a vet )d a )d
d d d d
 
 O O
O O
t t t

  
r rr r d PddP
D et N D
d d d
ou
25
• En le point O est fixe dans R
• En le point O’ est mobile dans R
 '
'( ) ( ) ( )
' ' ( )
(O
A A A O Av v v
O O Av
t t
m

        
  
  

r uuur uuur rr r r r
r r r
d d
O'A v )d O'A a d v v v d
d d
N v v d

26. 10. Relation entre torseur cinétique et torseur dynamique
26
• En le point O’ est mobile dans R
 '
'( ) ( ) ( )
' ' ( )
(O
A A A O Av v v
O O Av
t t
m

        
  
  

r uuur uuur rr r r r
r r r
d d
O'A v )d O'A a d v v v d
d d
N v v d
'
' '
ddP
D et N v P
d d
O
O O
t t

   
r rr r rr
i) Si O’ C :
d
N
d
C
C
t


rr
ii) Si O’ est fixe : '
'
d
N
d
O
O
t


rr

27. 11. Principe Fondamental de la Dynamique
• Enoncée: Le mouvement d’un système matériel (S) par rapport à un
référentiel  satisfait à l’équation torsorielle:
 
 O
ex O
F
t

d P
d
27
 
,
,
:
:
:
ex
ex O
O ex
ex
O ex
F
F
M
F
M

 

ur
uur
ur
uur
la torseur force des forcesextérieur
larésultante des forces extérieur
le momenten Odes forces extérieur

28. Cas de O’  C ,
,
O
ex O exF
t t


   
    
  
r rur urddP
et M
d d
 , ','
'
','
O
O ex O ex exO
O
O exO
F
t t
t



      
   
r ur uuur ur uuur urrr
r urrr
d d
M OO' P M OO'
d d
d
v P M
d
,
d
v P 0 M
d
C
C exC
t

   
r urrrr
28
12. Théorèmes Généraux de la Dynamique
12.1Théorèmes de la quantité de mouvement et du moment cinétique:

29. Si autre point O’ est mobile dans , il vient:
Soit:
29
12. Théorèmes Généraux de la Dynamique
12.2 Théorèmes de la somme dynamique et du moment dynamique :
    ,ex O exex C OO
F m F   
ur urrr
D a et N M
',' O ex exO F  
ur urr r
N +OO' D M +OO'
',' O ex exO F 
ur urr r
N M puisque D
En un point quelconque, mobile ou non, le moment dynamique est égal au
moment des forces extérieur.

30.    
   
,
,
:
:
Pour le point
Pour le point
d
ω M N
d
d
ω M
d
O
O exO OO O
C
C exC C C
I I
t
I I
t
O
C

 

 
    
   
r ur rr rr
r urr rr
30
12. Théorèmes Généraux de la Dynamique
12.3 Cas particulaire d’un solide est en rotation

31. 31
13. Energie cinétique
13.1 Définition
L’énergie cinétique d’un system matériel continu (S) en mouvement
par rapport à un repère fixe R est défini par:
𝐸 𝐶 =
1
2
∫ ( 𝑣 𝐴)2
𝑑𝑚
13.2 Théoreme Koënig à l’énergie cinétique
ù


 2
O est l'énrgie cinétique de dans le référentiel
du centre de masse
1
2
c
C c
d
cE m
E
v E
S

32. 32
14. Théorème de l’énergie cinétique
14.1 Travail et puissance d’une force
𝑊 = ∑ 𝐹𝑖. 𝑑𝑂𝐴𝑖 = ∑ 𝐹𝑖,𝑖𝑛𝑡 + 𝐹𝑖,𝑒𝑥𝑡 . 𝑑𝑂𝐴𝑖
𝑃 =
𝛿𝑊
𝑑𝑡
= ∑ 𝐹𝑖.
𝑑𝑂𝐴
𝑑𝑡
= ∑ 𝐹𝑖. 𝑣 𝐴 𝑖
= ∑ 𝐹𝑖,𝑖𝑛𝑡 + 𝐹𝑖,𝑒𝑥𝑡 𝑣 𝐴 𝑖

33. 33
14. Théorème de l’énergie cinétique
14.1 Théorème de l’énergie cinétique
𝐸 𝐶 = ∑
1
2
𝑚𝑖 𝑣 𝐴 𝑖
2
⇒
𝑑𝐸 𝐶
𝑑𝑡
= ∑𝑚𝑖
𝑑 𝑣 𝐴 𝑖
𝑑𝑡
. 𝑣 𝐴 𝑖
= ∑ 𝐹𝑖. 𝑣𝑖 = 𝑃 = 𝑃𝑖𝑛𝑡 + 𝑃𝑒𝑥𝑡
• 𝑃𝑖𝑛𝑡 = ∑ 𝐹𝑖,𝑖𝑛𝑡. 𝑣 𝐴 𝑖
: Puissance fournie au système par les forces intérieures ;
• 𝑃𝑒𝑥𝑡 = ∑ 𝐹𝑖,𝑒𝑥𝑡. 𝑣 𝐴 𝑖
: puissance fournie au système par les forces extérieures.

34.  
  
       


 
     
 
  
r r
r uuur uuurr r r
r r
rr ur2
2
0
0
2
0
1
Si
1 1 1
E (v ) d v OA d OA v d
2 2
E = .
2
1
=
1
= .
22
2
S S c
Ac A S S A
v v v
U
S
ssu u II u
34
15. Energie cinétique d’un solide indéformable
15.1 Cas de solide (S) a un point fixe O dans 

35. Dans le référentiel du centre de masse, l’énergie cinétique s’écrit:
   
 
        
  





   

   
        

  
rr r rr
r uur uurr r r r rr
r r
r2
2
1 1 1
E = v + = P v
1 1 1 1
E v d v CA d
2
CA v d
2 2 2 2
Comme
2 2
Ac A S S A C
c C C S C
S
v v v
C
S
C
CM
35
15. Energie cinétique d’un solide indéformable
15.2 Cas de solide (S) n’a pas un point fixe dans 

36. • Le nombre de degrés de liberté est égal au nombre de coordonnées qui
représentent la position de m moins le nombre de liaisons
• Il faut choisir une variable q pour repérer sa position. Cette variable est
appelée coordonnée généralisée
• Considérons le cas particulier d’une particule astreinte à se déplacer, sans
frottement, sur
une courbe plane contenue dans le plan xOy.
- Soit 𝐹 la résultante de toutes les forces agissant sur la particule. La relation
fondamentale de la dynamique s’écrit :
- Soit 𝑊 le travail fourni par la force 𝐹 lors d’un déplacement infinitésimal 𝛿 𝑟:
𝛿𝑊 = 𝐹. 𝛿 𝑟
36
16. Méthode de Lagrange
16.1 Equations de Lagrange pour une particule

37. - Le déplacement infinitésimal 𝛿 𝑟 peut s’écrire en fonction de la variation q
de la coordonnée généralisée q :
- Dans ce cas le travail 𝛿𝑊 peut se mettre la forme :
- q-composante de la force:
- En tenant compte de la relation fondamentale de la dynamique, cette expression
peut également s’écrire :
-
37
16. Méthode de Lagrange
16.1 Equations de Lagrange pour une particule

38. 38
16. Méthode de Lagrange
16.1 Equations de Lagrange pour une particule

39. 39
16. Méthode de Lagrange
16.1 Equations de Lagrange pour une particule

40. 40
16. Méthode de Lagrange
16.1 Equations de Lagrange pour une particule

41. 41
16. Méthode de Lagrange
16.1 Equations de Lagrange pour une particule

42. 42
16. Méthode de Lagrange
16.2 Cas des systèmes conservatifs

43. 43
16. Méthode de Lagrange
16.2 Cas des systèmes conservatifs

44. 44
16. Méthode de Lagrange
16.3 Cas des forces de frottement dépendant de la vitesse
• Equation de Lagrange

45. 45
16. Méthode de Lagrange
16.3 Cas des forces de frottement dépendant de la vitesse
• Fonction dissipation

46. 46
16. Méthode de Lagrange
16.3 Cas des forces de frottement dépendant de la vitesse
• Fonction dissipation

47. 47
16. Méthode de Lagrange
16.4 Cas d’une force extérieure dépendant du temps

48. 48
16. Méthode de Lagrange
16.4 Cas d’une force extérieure dépendant du temps

49. 49
16. Méthode de Lagrange
16.5 Système à plusieurs degrés de liberté

50. 50
17. Oscillations libres
17.1 Degrés de Liberté
• Systèmes à un seul degré de liberté

51. • Systèmes à deux degré de liberté
51
17. Oscillations libres
17.1 Degrés de Liberté

52. • Systèmes à trois degré de liberté
52
17. Oscillations libres
17.1 Degrés de Liberté

53. • Systèmes à multi degré de liberté
53
17. Oscillations libres
17.1 Degrés de Liberté

54. En général, un système vibrant est constitué :
• élément de ressort: stocker l'énergie potentielle,
• élément de masse ou de l'inertie: stocker l'énergie cinétique, et
• élément d’amortissement: l'énergie est peu à peu perdu,
54
17. Oscillations libres
17.2 Elémentaires de système de vibration

55. 55
• équivalente raideur de ressort
17. Oscillations libres
17.3 élément de ressort

56. 56
• équivalente masse-exemple:
32
2 1 3 1
1 1
ll
x = x and x = x
l l
& & & & eq 1x = x& &
  2 2 2 21 1 1 1
1 1 2 2 3 3 eq eq2 2 2 2
m x m x m x m x& & & &
   
     
   
2 2
32
eq 1 2 3
1 1
ll
m m m m
l l
17. Oscillations libres
17.4 élément de de masse

57. 57
• L'amortissement visqueux:
Sur la base de fluide visqueux s'écoulant à travers l'orifice
ou fente. La force d'amortissement  vitesse relative entre
les extrémités

• Coulomb (frottement sec) d'amortissement:
Basé sur le frottement entre les surfaces non lubrifiées
La force d'amortissement est constante et opposée à la
direction de déplacement
17. Oscillations libres
17.5 élément d’amortissement

58. 58
 L'équation différentielle de mouvement est :
2
0 0x x &&
0 0
0
2
est la ,et T lapulsation propre période propre



 
 Solution générale : cos( )x A t  
17. Oscillations libres
17.6 Vibration libres non amorties du système translation

59. Une masse fixée à l'extrémité de l'arbre est un système
simple torsion. La masse de l'arbre est considéré comme
faible par rapport à la masse du disque et est donc négligée.
59
Le couple qui produit torsion est donnée par :
Mt= kt  , kt est raideur de torsion
Par le théorème du moment cinétique:
0G tI k  &&
0 0 0
0
0
cos( ) sin( ) ,solution: (t)=
avec t
G
t t
k
I

   




&
17. Oscillations libres
17.6 Vibration libres non amorties du système torsion

60. 60
• L'équation différentielle du mouvement:
La force d'amortissement visqueux est proportionnelle à la vitesse de de la masse 𝑥 et
agissant dans le direction opposée à la vitesse de la masse et peut être exprimé comme
𝐹 = 𝑐 𝑥
où c est la constante d'amortissement ou le coefficient d'amortissement visqueux
L'équation différentielle du mouvement:
2 2
0 02 0 , avec = et
2
c k
x x x
m m
      && &
17. Oscillations libres
17.6 Vibration libres amorties avec amortissement visqueux
𝑇𝑒𝑙𝑠 𝑞𝑢𝑒
𝜆 =
𝑐
2𝑚
𝑠−1 : 𝐹𝑎𝑐𝑡𝑒𝑢𝑟 𝑑′ 𝑎𝑚𝑜𝑟𝑡𝑖𝑠𝑚𝑒𝑛𝑡.
ξ =
𝜆
𝜔0
𝑠𝑎𝑛𝑠 𝑢𝑛𝑖𝑡 : 𝑅𝑎𝑝𝑝𝑜𝑟𝑡 𝑑′ 𝑎𝑚𝑜𝑟𝑡𝑖𝑠𝑒𝑚𝑒𝑛𝑡

61. 61
• Solutions générale
2
0
2 2
0
2 2
0
2 0
L'équation caractéristique: 2 0
'=
x x x
r r
 
 
 
  
  
 
&& &
 
0
2 2 2
0
(i) si ' < 0 < (0 1) : faiblement amorti
Poson
La solution s'écrit:
( ) cos( )
ou bien: ( ) Acos( ) sin ( )
t
t
x t ae t
x t e t B t


  
  
 
 


   
 
 
 
o
17. Oscillations libres
17.6 Vibration libres amorties avec amortissement visqueux

62. 62
1 2
0
1 2 0
1 2
0
2 2
0
1 2
(ii) si ' 0 ( 1) : amortissement critique
La solution s'écrit: ( ) (C +C t)
(iii) si ' > 0 > ( >1): fortement amorti
Posons
La solution s'écrit: ( )
t
r t r
r r
x t e
x t C e C e

  
 
  
  

    
    

 
 
 
o
o  2 2 2 2
0 0
1 2
t tt t
e C e C e
      
 
17. Oscillations libres
17.6 Vibration libres amorties avec amortissement visqueux
• Solutions générale

63. 63
17. Oscillations libres
17.6 Vibration libres amorties avec amortissement visqueux
• Graph
n
2

d
2

Overdamped ( 1) 
Underdamped ( 1) 
Underdamped ( 0 ) 
Critically
damped ( 1) 

64. • Décrément logarithmique
Définition : C’est le logarithme du rapport de 2 amplitudes successives des
oscillations amorties.
𝛿 = ln
𝑥 𝑡1
𝑥 𝑡2
, 𝑡2 = 𝑡1 + 𝑇𝑎
64
-3
-2
-1
0
1
2
3
0 2 4 6
t1
t2
x1
x2
d
17. Oscillations libres des systèmes à un degré de liberté
17.6 Vibration libres amorties avec amortissement visqueux

65. Décrément logarithmique
65
-3
-2
-1
0
1
2
3
0 2 4 6 8
t1
t2
x1
x2
d
 
1
2
1
1
t
0 11
2 1 1t
2 0 2
2 1 1
t
1
t
2
1
2
X e cos( t )x 2
, Laisser t t t
x X e cos( t )
cos( t ) cos( 2 t ) cos( t )
x e
et e
x e
x
ln
x




 
  

 
      
 



 

    

     
 
 
  
 

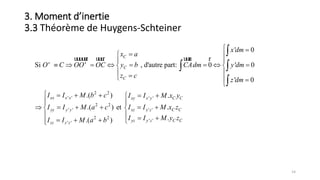
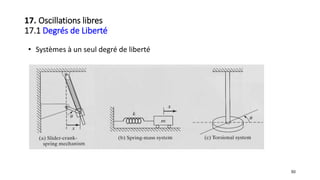
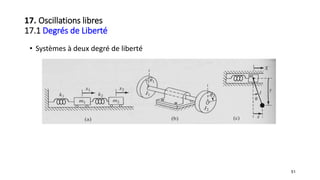
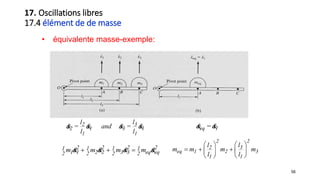
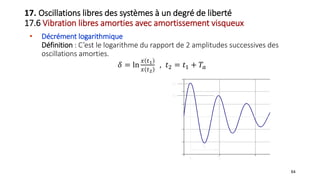
66. 66
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
Time [s]
Amplitude[m]
x1
x2
Xm+1
 
j3 m1 1 2
m 1 2 3 4 m 1 j 1
m m1 1
m 1 m 1
xx xx x x
.... ,mais e
x x x x x x
x x1
e e , Donc: ln
x m x

 

  
 

 
 
    
 

67. Exemple(4)
67
Trouver la réponse du système
représenté à la droite si le bloc est
tiré vers le bas par 15 cm et
reste sous forme libérée
Ré.:

68. Vibration libres amorties avec amortissement Coulomb
68
Case 1. Case 2.

69. 69

70. 70

71. 71

72. 72

73. 73

74. 82
Régime pseudo-périodique :
amortissement faible (suite)
La constante de temps
Quelque soit le type de régime, l'amortissement des oscillations
dépend du terme exponentiel e−λt , λ est appelée constante
d'amortissement . Nous appelons constante de temps τ , l'intervalle
de temps telle que
La pseudo-période
Nous pouvons en déduire l'expression mathématique de
la pseudo-période T′
ou

75. 83
Régime pseudo-périodique :
amortissement faible (suite)
La constante de temps
Quelque soit le type de régime, l'amortissement des oscillations
dépend du terme exponentiel e−λt , λ est appelée constante
d'amortissement . Nous appelons constante de temps τ , l'intervalle
de temps telle que
La pseudo-période
Nous pouvons en déduire l'expression mathématique de
la pseudo-période T′
ou

76. Graphique
84

77. Aspects énergétiques
85
Il va y avoir obligatoirement par la présence de la force de frottement
qui est une force à travail non conservatif et résistant, une diminution
de l'énergie mécanique de l'oscillateur harmonique amorti. Pour
étudier cela, nous allons nous limiter à l'étude du cas où nous avons
des oscillations donc au régime pseudo-périodique. Dans ce cas nous
avons vu que l'élongation et la vitesse ont les expressions suivantes
en fonction du temps :
Nous allons en déduire les expressions respectives en fonction du temps
de l'énergie cinétique, de l'énergie potentielle et de l'énergie mécanique.

78. Energie cinétique
86

79. Cas d'un amortissement très faible
87
Lorsque l'action de la force de frottement est très faible, nous
savons que λ ≪ ω0 donc que Il s'en suit que T′ ≃ T0 et ω′ ≃ ω0.
Nous pouvons donc recalculer l'énergie mécanique de l'oscillateur dans
cette situation en simplifiant son expression en tenant compte de
l'amortissement très faible.

80. 88

81. 89

82. L'oscillateur harmonique en régime forcé
90
Ceci rend très important l'étude de l'excitation sinusoïdale,
la force dans ce cas, prend la forme suivante :
 Equation du mouvement :

83. L'oscillateur harmonique en régime forcé (suite)
91
 Résolution de l'équation différentielle
x(t) = xH(t) + xP (t)
• xH(t) : la solution générale de l'équation différentielle sans second
membre (appelée aussi équation homogène), et une deuxième xP (t), qui
est une solution particulière de l'équation complète.
• xH(t) = e-t ×(C.sin(’t)+D.cos(’t)): régime transitoire
xP (t)= A.cos( t +) : régime forcé ou régime permanent

84. L'oscillateur harmonique en régime forcé (suite)
92
 Détermination de la solution forcée en utilisant les nombres
complexes
Nous pouvons montrer en mathématiques que si une solution xP (t) en
cosinus, comme celle qui est écrite précédemment, est une solution
particulière de l'équation différentielle d'intérêt alors une solution en
Asin(Ωt + ϕ) est aussi une solution particulière possible de l'équation
différentielle avec un second membre changé en F/msin(Ωt). Donc un
nombre complexe, de la forme suivante A×(cos(Ωt+ϕ)+i sin(Ωt+ϕ)), sera lui
solution de l'équation différentielle suivante :

85. L'oscillateur harmonique en régime forcé (suite)
93
 Détermination de la solution forcée en utilisant les nombres
complexes

86. Etude du régime permanent : phénomène de résonance en amplitude
94
Nous avons :
Pour que cette dérivée soit nulle, il sut donc que:
2 2 2 2 2
0
0
ou 2 0 2 r   
 
          (pulsation de résonance)

87. Etude du régime permanent : phénomène de résonance en amplitude
95
Nous l'appellerons la condition de résonance en amplitude.
00 2r     
Si nous définissons cette grandeur en fonction de Q et ω0, nous
obtenons
La condition de résonance devient
avec on appelle le facteur de qualité
 Notion de résonance en amplitude du mouvement

88. Etude du régime permanent : phénomène de résonance en amplitude
96
 Caractérisation physique de la résonance en amplitude
Nous pouvons maintenant calculer la valeur de l'amplitude lorsque la
pulsation de l'excitateur est effectivement égale à la pulsation de
résonance:

89. Etude du régime permanent : phénomène de résonance en amplitude
97
 Caractérisation physique de la résonance en amplitude (suite)
Ensuite, en sortant de la racine 2λ, nous obtenons

90. 98

91. Résonance en vitesse
99
 Détermination de la vitesse
Nous allons aussi calculer la vitesse de l'oscillateur en régime forcé. A
partir de l'expression complexe de l'amplitude xP(t), il est très simple de
calculer une expression complexe de la vitesse, en effet nous avons
obtenu :

92. Résonance en vitesse
100
 Détermination de la vitesse (suite)

93. Résonance en vitesse
101
 Phénomène de résonance en vitesse
L'amplitude maximale de la vitesse obtenue à la résonance est :

94. Impédance mécanique
102
Sous l'effet d'une cause excitatrice, la force excitatrice, l'effet produit
est le mouvement de l'oscillateur à la vitesse V P (t), nous appelons
impédance mécanique d'un oscillateur, le rapport cause sur effet, donc
le rapport de l'amplitude complexe de la force excitatrice

95. Conséquences pour l'énergie mécanique de l'oscillateur
harmonique
103
 Expression de la puissance moyenne absorbée par
l'oscillateur
La puissance instantanée absorbée par l'oscillateur et fournie par
l'excitateur est donc :
Nous pouvons obtenir l'expression de cette puissance instantanée en
remplaçant Fexc(t) par

96. Conséquences pour l'énergie mécanique de l'oscillateur
harmonique
104
 Expression de la puissance moyenne absorbée par
l'oscillateur
Nous calculons alors la moyenne de P(t) sur une période T de
l'excitateur :

97. Bilan énergétique
105
Nous pouvons étudier différemment cet aspect en passant par le
théorème de l'énergie cinétique :

98. 106
17. Oscillations libres des systèmes à un degré de liberté
17.1 Oscillations non amortizes
17.1.1 Oscillateur linéaire
Un système oscillant à un degré de liberté est habituellement repéré à l’aide d’une coordonnée
généralisée q qui est l’écart par rapport à la position d’équilibre stable. Le mouvement vibratoire
est dit linéaire s’il est régi par une équation différentielle harmonique de la forme :
𝑞 + 𝜔0
2
𝑞 = 0
Cette équation est appelée équation différentielle de l’oscillateur harmonique simple.

99. 107
17. Oscillations libres des systèmes à un degré de liberté
17.1 Oscillations non amortizes
17.1.2 Energie cinétique

100. 108
17. Oscillations libres des systèmes à un degré de liberté
17.1 Oscillations non amortizes
17.1.3 Energie potentielle