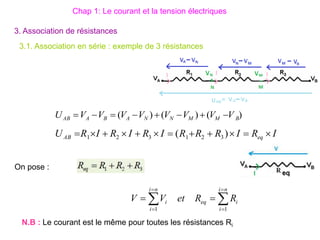
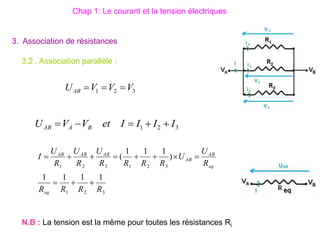
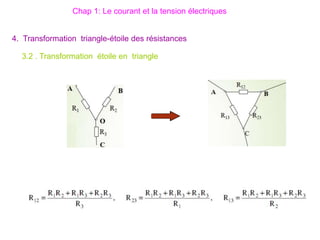
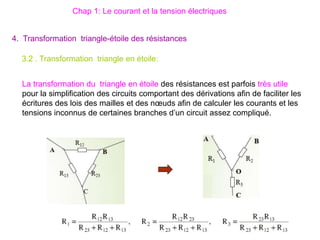
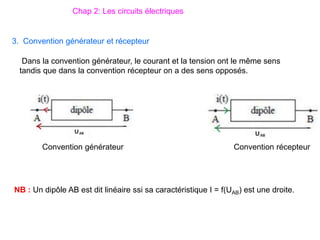
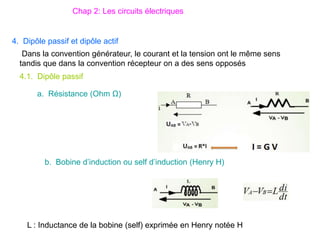
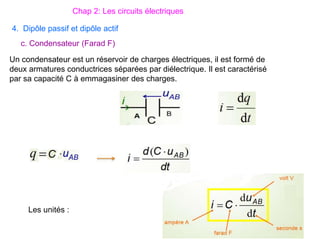
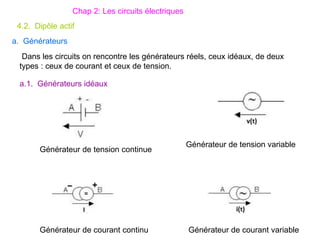
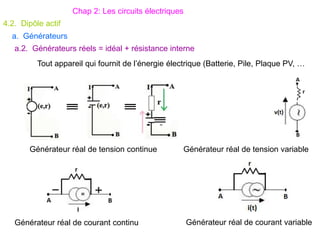
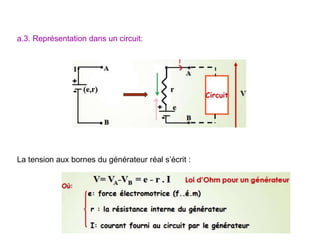
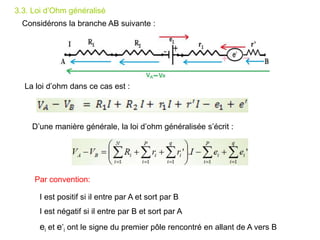
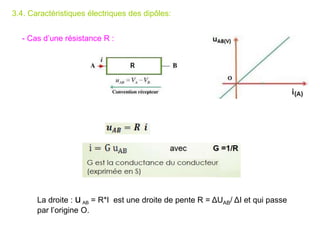
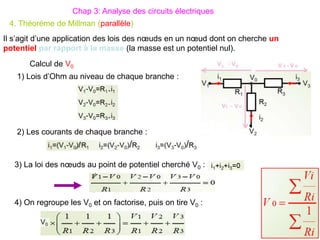
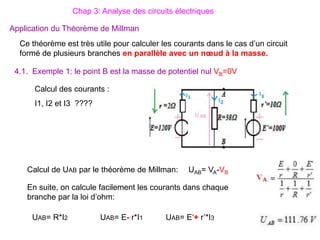
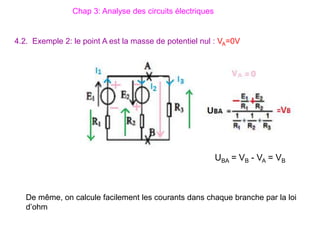
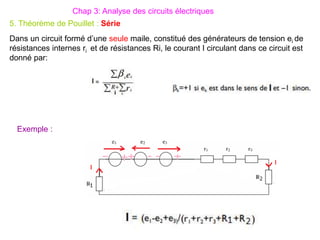
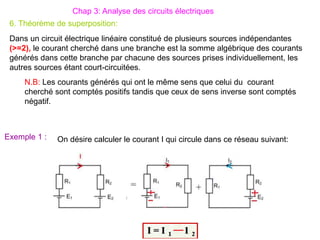
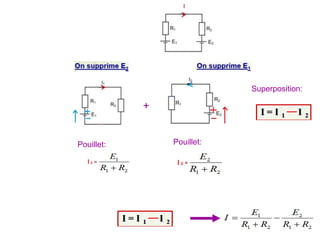
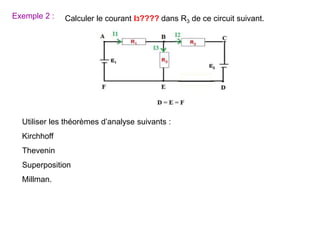
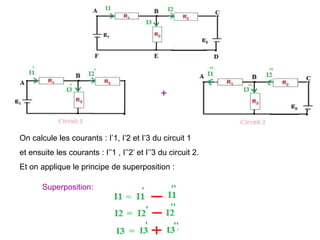
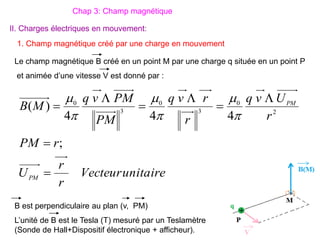
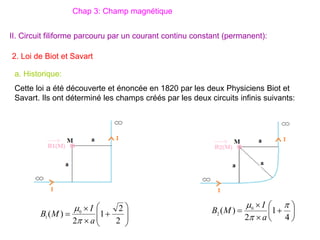
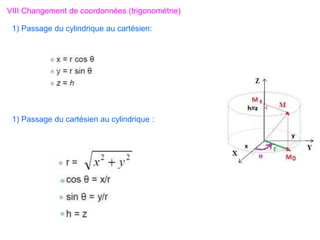
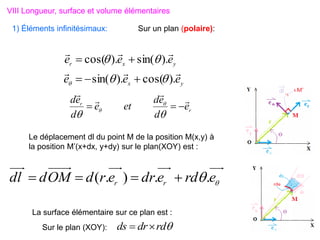
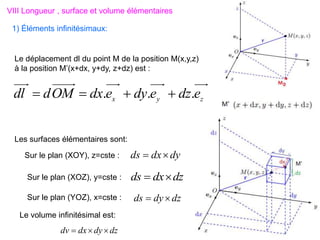
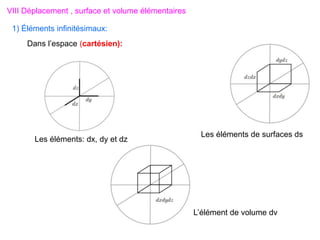
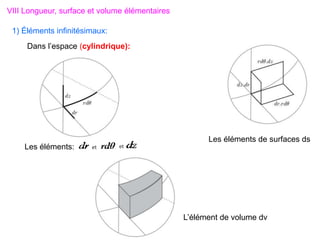
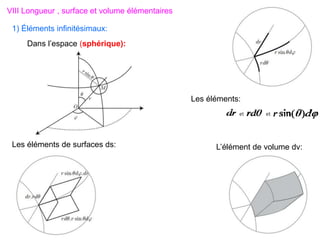
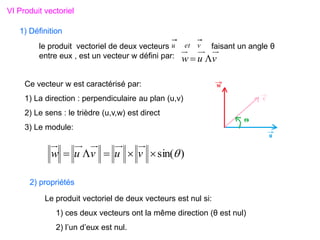
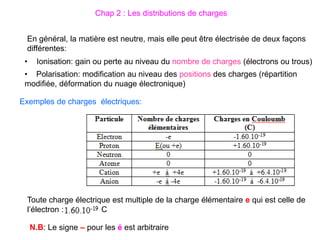
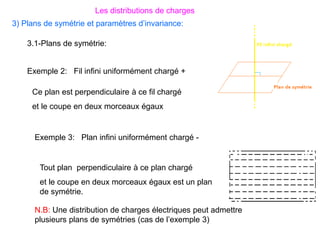
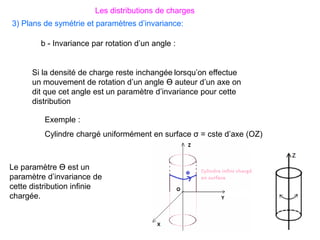
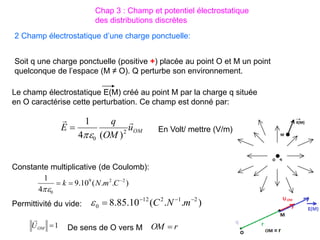
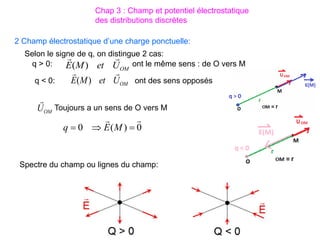
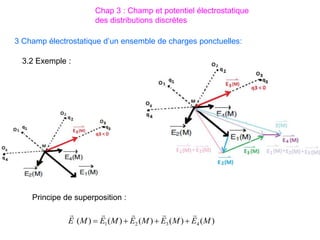
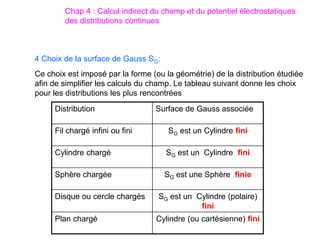
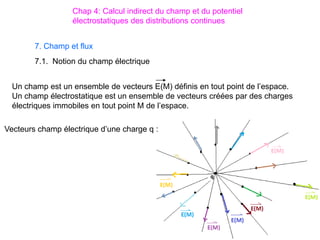
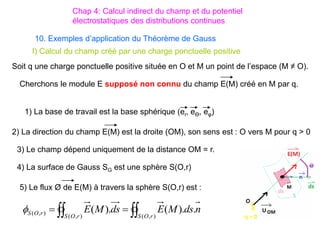
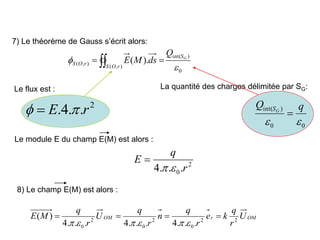
Le document traite des systèmes de coordonnées en électricité, notamment les systèmes cartésiens, polaires, cylindriques et sphériques, précisant leur définition et leur utilisation pour localiser des points dans différents espaces. Il aborde également les formules trigonométriques et les changements de coordonnées entre ces systèmes, ainsi que les éléments infinitésimaux pour le calcul de longueurs, surfaces et volumes. Enfin, des formules pour exprimer les déplacements et les surfaces élémentaires sont fournies.






![]
2
,
0
[
,
)
,
(
]
,
0
[
,
)
,
(
'
OM
OX
OM
OZ
OM
r
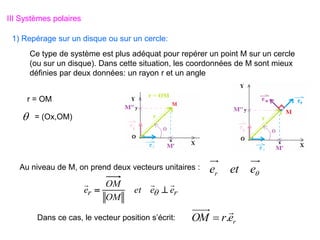
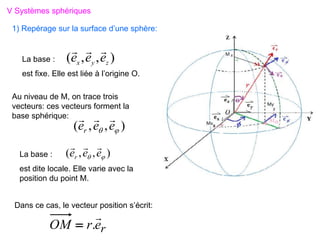
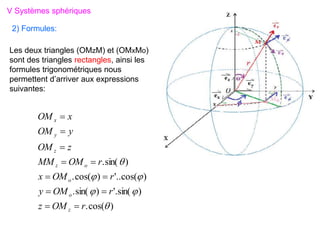
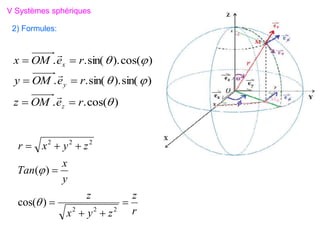
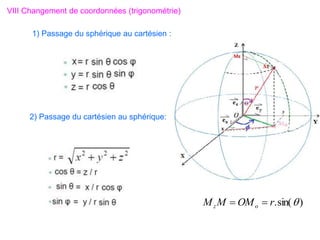
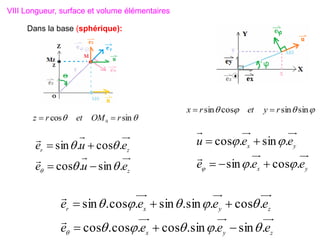
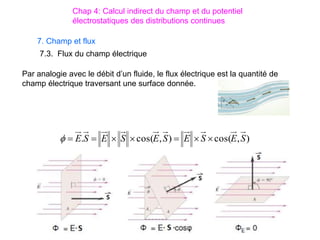
V Systèmes sphériques
Ce type de système est plus adéquat pour repérer un point M sur la surface
d’une sphère. Dans cette situation, les coordonnées de M sont : r, θ et
telles que :
1) Repérage sur la surface d’une sphère:
θ : Colatitude suivant les méridien
: Longitude (Azimuth)
suivant les parallèles
](https://image.slidesharecdn.com/m312electricitbcg-240207230507-80f90bdb/85/M312_Electricite_BCG-ppt-12-320.jpg)

























































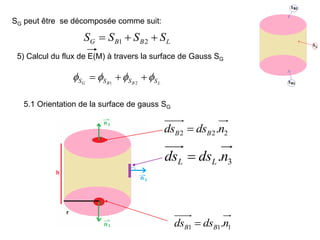

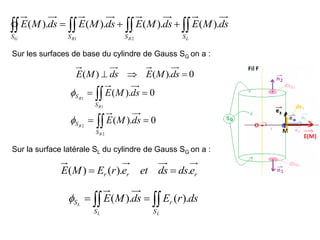
![Sur la surface latérale SL du cylindre de Gauss SG le champ E(M) est constant
car r est fixe sur cette surface SL :
r
r
r e
r
f
e
r
E
M
E .
)
(
.
)
(
)
(
]
2
,
2
[
;
]
2
,
0
[
;
h
h
z
fixe
est
r
dz
rd
dsL
L
L
L
L
S
r
S
r
S
S ds
r
E
ds
r
E
ds
M
E )
(
).
(
).
(
Sur la surface latérale SL du cylindre de Gauss SG la surface élémentaire dsL
s’écrit :
h
r
dz
d
r
dz
rd
ds
h
h
h
h
S
L
L
.
2
.
2
/
2
/
2
0
2
2
2
0
)
(
.
.
.
2
).
( r
E
h
r
ds
M
E r
S
S
L
L
)
(
.
.
.
2
).
(
2
1
r
E
h
r
ds
M
E r
S
S
S
S
S
G
L
B
B
G
](https://image.slidesharecdn.com/m312electricitbcg-240207230507-80f90bdb/85/M312_Electricite_BCG-ppt-96-320.jpg)

![Pour le potentiel V(M), Il y a invariance de la distribution de charges par
translation selon z et par rotation par ϴ, donc V ne dépend ni de r ni de ϴ ; il
dépend uniquement de r :
)
(
)
( r
V
M
V
r
r e
dr
r
dV
e
r
V
r
r
V
grad .
)
(
).
(
)
(
)
(
)
,
,
(
).
(
)
( r
V
grad
z
r
V
grad
e
r
E
M
E r
r
Par intégration on obtient :
r
dr
r
dV
r
Er
.
2
)
(
)
(
0
)]
[ln(
2
)]
[ln(
2
)
(
)
(
)]
[ln(
2
)
(
)
(
0
0
0
0
0
0
0
0
0
r
r
V
r
r
r
V
r
V
r
r
r
V
r
V
0
0
0
)]
[ln(
2
2 0
0
)
(
)
(
r
r
r
r
r
V
r
V
r
r
dr
dV
](https://image.slidesharecdn.com/m312electricitbcg-240207230507-80f90bdb/85/M312_Electricite_BCG-ppt-98-320.jpg)