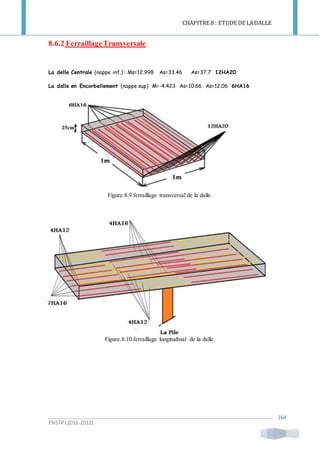
Ce document traite de l'étude d'une dalle en béton armé utilisée pour la couverture d'un pont, en se concentrant sur la flexion locale et générale. Il décrit les méthodes de calcul des moments fléchissants pour différentes configurations de dalles et les charges permanentes et dynamiques à considérer. Les résultats incluent des valeurs spécifiques de moments fléchissants pour diverses charges et configurations de dalles, ainsi que des coefficients de majoration pour les surcharges militaires et civiles.



![CHAPITRE 8 : ETUDE DE LADALLE
ENSTP(2011-2012)
153
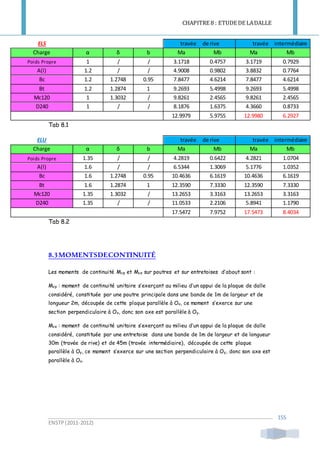
Convoi D240 :
Travée de rive :
a = 5.5 m ; b = 30 m =>ρ=
𝑎
𝑏
= 0.183 =>
1
ρ
= 5.45
ρ = 0.183 => M1 = 0.024 ;
1
ρ
= 5.45 => M2 = 0
u’ = u + 2E = 3.2 + 2x0.185 = 3.57 m
v’ = v + 2E = 18.6 + 2x0.185 = 18.97 m
=> Q = 4.03t/m2 x 3.57 x 18.97 = 272.92 t
Ma = (M1 + νM2) Q = (0.03 + 0.2(0)) x 272.92= 8.1876 t.m/ml
Mb = (M2 + νM1) Q = (0 + 0.2 (0.03)) x 272.92= 1.6375 t.m/ml
Travée Intermédiaire :
a = 5.5 m ; b = 45 m =>ρ=
𝑎
𝑏
= 0.122 =>
1
ρ
= 8.18
ρ = 0.122 => M1 = 0.016 ;
1
ρ
= 8.18 => M2 = 0
u’ = u + 2E = 3.2 + 2x0.185 = 3.57 m
v’ = v + 2E = 18.6 + 2x0.185 = 18.97 m
=> Q = 4.03t/m2 x 3.57 x 18.97 = 272.92 t
Ma = (M1 + ν M2) Q = (0.016 + 0.2(0)) x 272.92= 4.366 t.m/ml
Mb = (M2 + ν M1) Q = (0 + 0.2 (0.016)) x 272.92= 0.8733 t.m/ml
Calcul de coefficient de majoration dynamique
L = inf. [sup (entre axe des poutres de rive, largeur roulable) ; portée de la poutre]
L = inf. [sup (5.5, 9.5) ; 22.5] = 9.5 m
G : poids total d’une section de couverture sur un carré de coté 7.5 m
G = (9.5 x 9.5 x 2.5 x 0.25) + 9.5 x 9.5 x 2.2 x 0.08) = 72.29 t](https://image.slidesharecdn.com/etudedunedalle-180223083157/85/Etude-d-une-dalle-6-320.jpg)