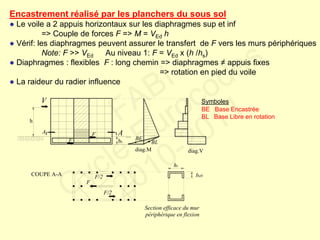
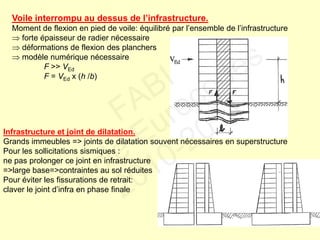
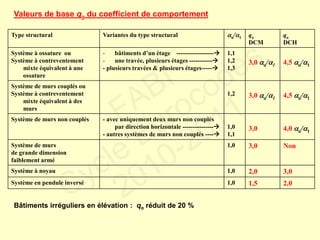
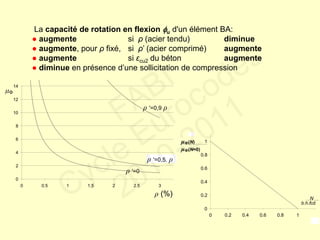
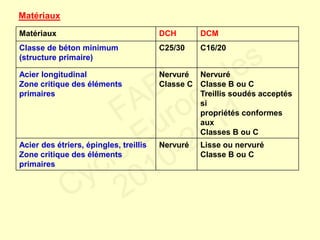
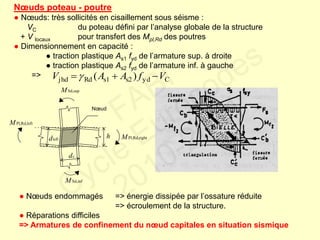
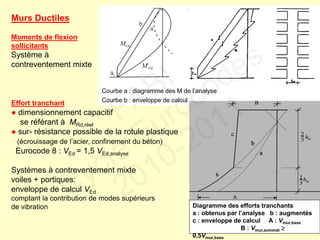
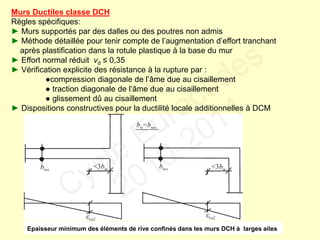
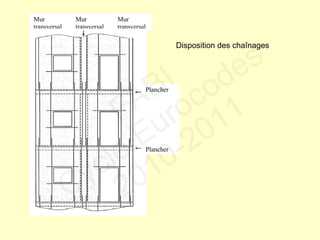
Le document traite des normes de calcul des structures en béton armé pour leur résistance aux séismes selon l'Eurocode 8. Il présente les phénomènes ductiles et non ductiles en rapport avec le matériel et les conditions sismiques, ainsi que les types de structures appropriées et les critères de projet en fonction des risques sismiques. Des recommandations spécifiques et des contre-mesures sont fournies pour garantir la ductilité et la sécurité des constructions face aux tremblements de terre.





![Cisaillement alterné: pas de poteaux courts
Pourquoi?
Pour atteindre en premier la résistance en flexion, il faut: MRd/MEd < VRd/VEd
MEd , VEd : liées
Elément bi-encastré de longueur L: MEd = VEd x L/2
Pour plastifier par flexion avant ruine en cisaillement:
[2MRd/(VEd x L)] < VRd/VEd
=> L > 2MRd/VRd,max
Préconisé: L > 3MRd/VRd,max
FABI
Cycle Eurocodes
2010-2011](https://image.slidesharecdn.com/2010062205baplumierdegee-150310060024-conversion-gate01/85/20100622-05-ba_plumier_degee-6-320.jpg)




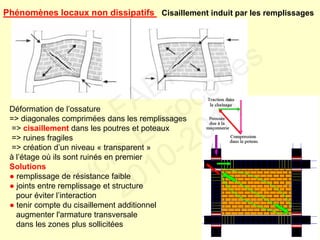
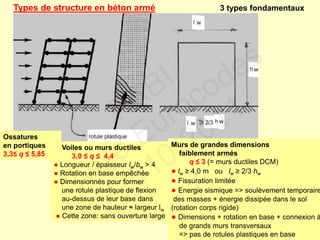







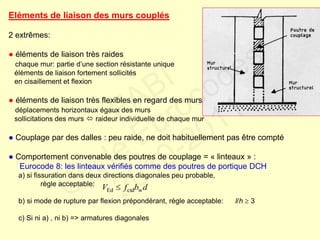
![Contraintes géométriques
● Excentricité max de l’axe des poutres p.r. axe des poteaux ≤ bc/4
bc :dimension du poteau perpendiculaire à l’axe de la poutre
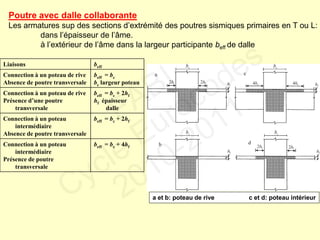
● Largeur bw d’une poutre sismique primaire requise pour bénéficier de l’effet favorable
de la compression du poteau sur l’adhérence des barres horizontales
passant à travers le nœud : bw ≤ min [ bc+hw ; 2bc] hw : hauteur de poutre
● Dimension min de la section transversale des poteaux sismiques primaires
≥ 1/10 de la plus grande distance entre le point d’inflexion et les extrémités du poteau
pour la flexion dans un plan parallèle à la dimension de poteau considérée
(sauf si ≤ 0,1 ).
● Epaisseur max bwo de l’âme des murs ductiles ou de grandes dimensions peu armés:
bwo max(0,15m, hs/20) hs est la hauteur libre d’étage en m
FABI
Cycle Eurocodes
2010-2011](https://image.slidesharecdn.com/2010062205baplumierdegee-150310060024-conversion-gate01/85/20100622-05-ba_plumier_degee-22-320.jpg)






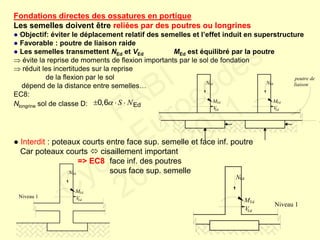
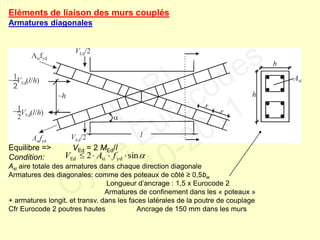
![Vérifications des poteaux. Dimensionnement “poutres faibles - poteaux forts”
[rotules plastiques dans les poutres]
NEd≤ 0,65 NRd
Résistance du poteau à la flexion
Mi,d = Rd MRc,i MRb / MRc
MRc,i valeur de calcul de la résistance à la flexion
du poteau à l’extrémité i
MRc,i du poteau et MRc sont calculés
en considérant l’interaction avec l’effort normal
Rd coefficient de surdimensionnement; pour
la sur- résistance possible de la rotule plastique
Rd = 1,1 (DCM) Rd = 1,3 (DCH)
Résistance du poteau à l’effort tranchant
Efforts tranchants de calcul :
se basant sur l’équilibre du poteau sous les Mi,d
Résistance au cisaillement:
VRd=0.9bwdwfywdcot 22o45o Vcd=0
FABI
Cycle Eurocodes
2010-2011](https://image.slidesharecdn.com/2010062205baplumierdegee-150310060024-conversion-gate01/85/20100622-05-ba_plumier_degee-31-320.jpg)
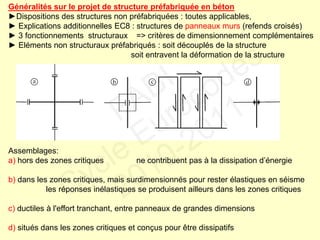
![Vérifications des poteaux. Dimensionnement “poutres fortes - poteaux faibles”
[rotules plastiques dans les poteaux]
Résistance du poteau à la flexion
MRb = Mpl,Rd ≥ MEd
Mpl,Rd tient compte de l’interaction M-N
Résistance du poteau à l’effort tranchant
Les moments sollicitants de calcul Mi,d
aux extrémités des poteaux sont les Mpl,Rd
Les efforts tranchants de calcul sont déterminés
en se basant sur l’équilibre du poteau sous l’effet
des moments d’extrémité Rd Mi,d
Rd = 1,1 (DCM) Rd = 1,3 (DCH)
FABI
Cycle Eurocodes
2010-2011](https://image.slidesharecdn.com/2010062205baplumierdegee-150310060024-conversion-gate01/85/20100622-05-ba_plumier_degee-32-320.jpg)
















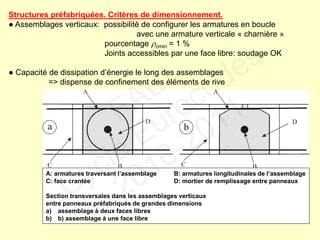




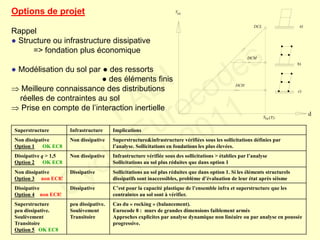
![Résistances à la fondation
pour la reprise du cisaillement horizontal VEd:
● frottement FRd à l’interface horizontale béton – sol
● frottement latéral
faces verticales de la fondation parallèles à VEd
● butée Epd
si sol mobilisé compact le long de la face verticale
partie supérieure des pieux
[coefficient de poussée des terres passives Kp]
● Addition de toutes les réactions possibles en valeur max:
Eurocode 8 : non
max combiné frottement + butée
= FRd + 0,3 x Epd
Pour des semelles, si compactage du remblai
ou coulage de la semelle
contre surface verticale propre de sol
= FRd + Epd
NEd
MEd
VEd
Epd
FRd
VEd
Epd
E'pd
RC
◄▬ ◄▬ ◄▬
FRd
FABI
Cycle Eurocodes
2010-2011](https://image.slidesharecdn.com/2010062205baplumierdegee-150310060024-conversion-gate01/85/20100622-05-ba_plumier_degee-61-320.jpg)