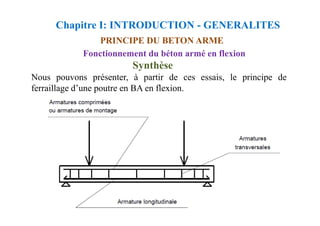
Le document traite du béton armé, une combinaison de béton et d'acier, et met en avant ses propriétés, avantages et inconvénients. Il décrit également les normes BAEL pour la construction, en se concentrant sur le dimensionnement des structures pour garantir leur sécurité et durabilité. Les actions et sollicitations sur les structures, ainsi que les états limites, sont également abordés pour assurer une conception adéquate.




































































![La longueur d’ancrage
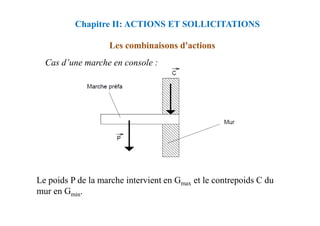
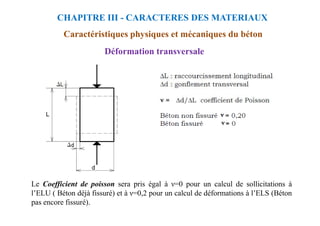
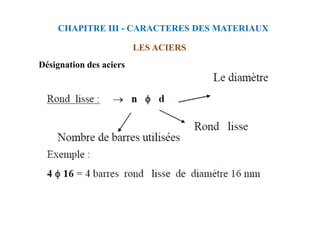
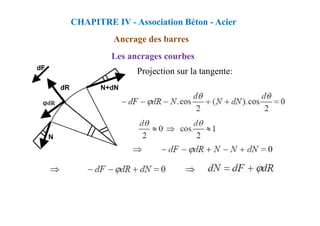
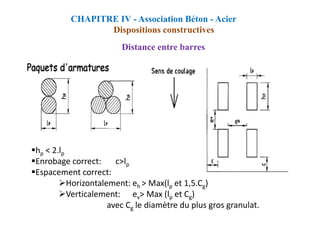
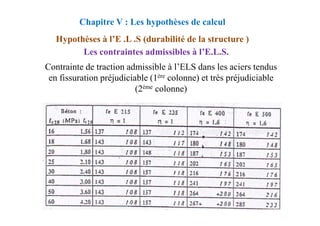
CHAPITRE IV - Association Béton - Acier
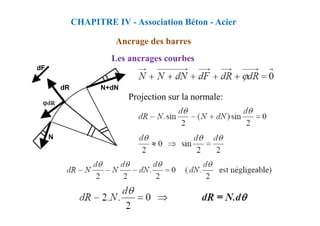
Ancrage des barres
Les ancrages courbes
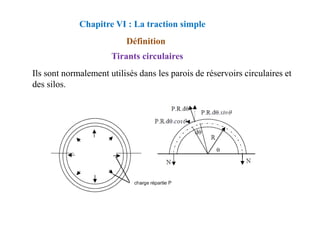
On a:
La= L2+r.cos(α/2)+ϕ/2
or on a:
or on a:
α/2 = (π/2)-(θ/2)
donc:
cos(α/2) = 1-cos(θ/2)
d’où:
La=L2+r[1-cos(θ/2)]+ ϕ/2](https://image.slidesharecdn.com/coursbael-230209200545-b344fe2d/85/Cours_BAEL-pdf-90-320.jpg)










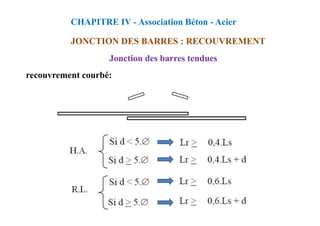
















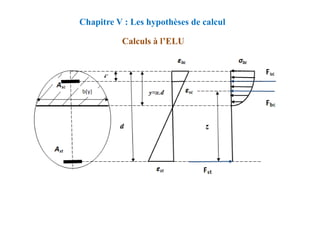


























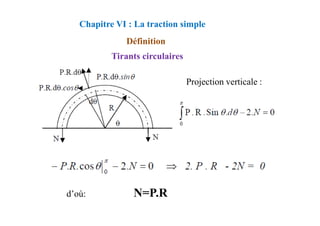























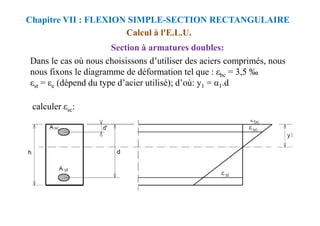


























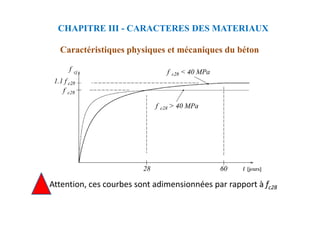
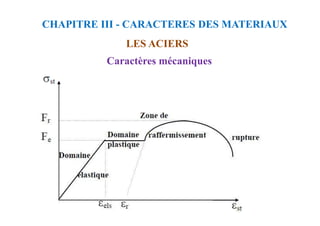
![CALCUL A L’ELU :
Section sans armatures comprimées :
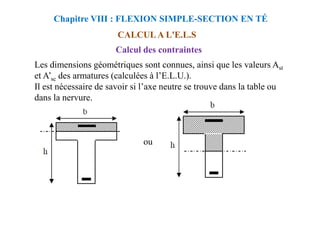
Chapitre VIII : FLEXION SIMPLE-SECTION EN TÉ
L’équilibre des efforts:
( )
F
F
A
F
F
F
1
2
1
2
1
+
=
⇒
+
= ( )
st
b
b
st
b
b
st F
F
A
F
F
F
σ
1
2
1
2
1
+
=
⇒
+
=
( )
[ ]
st
bc
st d
b
h
b
b
A
σ
σ
α 0
2
0
0 8
,
0
+
−
=](https://image.slidesharecdn.com/coursbael-230209200545-b344fe2d/85/Cours_BAEL-pdf-217-320.jpg)
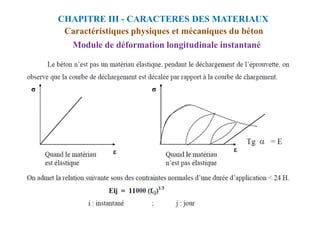
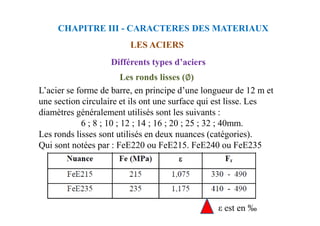
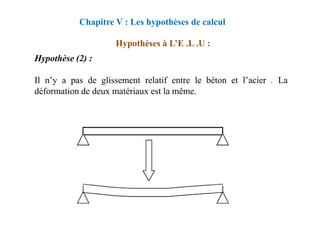
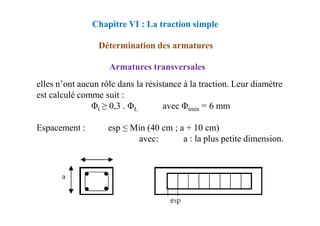
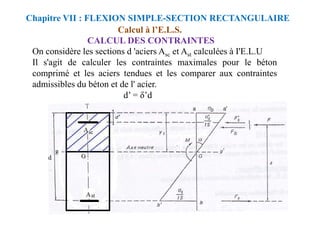
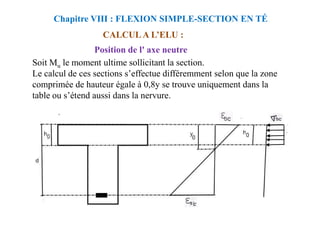
![CALCUL A L’ELU
Section avec armatures comprimées
Chapitre VIII : FLEXION
SIMPLE-SECTION EN TÉ
Si: 2> R, on se fixe: 2= R et α2=αR → yR et εst=εe
σst=fe/γs . sc
sc
d
d
σ
α
ε →
−
=
'
1
5
,
3 00
0
⇒
=
= d
b
M
M σ
µ 2
2 M
M
M
1
−
−
=
⇒
=
= bc
R
R
b d
b
M
M σ
µ 2
0
2
( ) sc
R
b
u
sc
d
d
M
M
M
A
σ
'
−
−
−
=
st
st
sc
b
b
st A
F
F
F
F σ
.
2
1
=
+
+
=
( )
[ ]
s
e
sc
sc
bc
R
bc
st
f
A
d
b
h
b
b
A
γ
σ
σ
α
σ
1
8
,
0 0
0
0 +
+
−
=
( )
−
−
=
2
0
0
0
1 h
d
h
b
b
M bc
b σ](https://image.slidesharecdn.com/coursbael-230209200545-b344fe2d/85/Cours_BAEL-pdf-219-320.jpg)

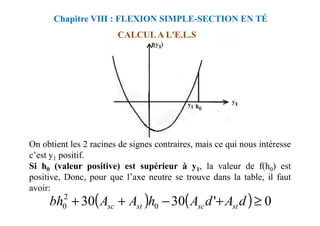


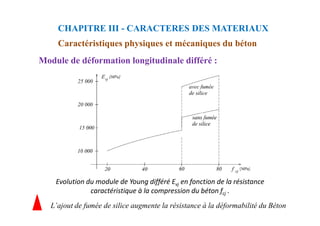
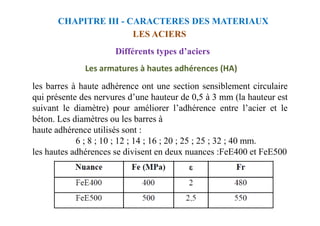
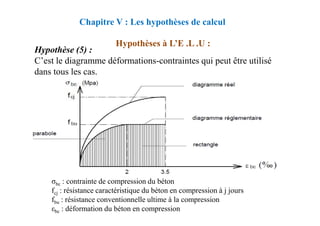
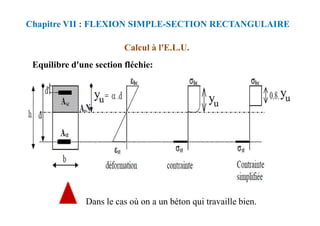
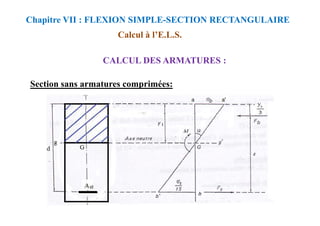
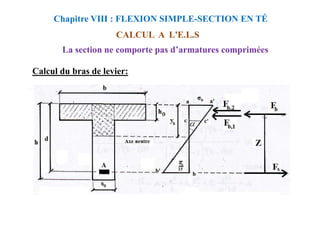
![donc:
Nous déterminons y à partir de cette équation.
Chapitre VIII : FLEXION SIMPLE-SECTION EN TÉ
CALCUL A L'E.L.S
Calcul des contraintes lorsque l’axe neutre se trouve dans la
nervure:
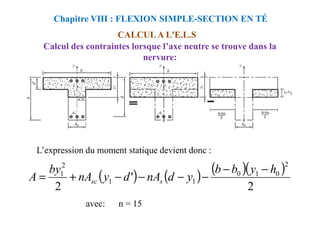
( ) ( )
[ ] ( ) ( )
[ ] 0
'
30
30
2 2
0
0
1
0
0
2
1
0 =
+
+
−
−
+
+
−
+
= sc
s
sc
s A
d
dA
h
b
b
y
A
A
h
b
b
y
b
A
Nous déterminons y1 à partir de cette équation.
Les deux solution de l’équation: a.x2 + b.x + c = 0
Dans notre cas on s’intéressera à la valeur positive:
a
ac
b
b
x
2
4
2
2
,
1
−
±
−
=
a
ac
b
b
x
2
4
2
1
−
+
−
=](https://image.slidesharecdn.com/coursbael-230209200545-b344fe2d/85/Cours_BAEL-pdf-226-320.jpg)

![On a:
CALCUL A L'E.L.S
Chapitre VIII : FLEXION SIMPLE-SECTION EN TÉ
Calcul des contraintes lorsque l’axe neutre se trouve dans la
nervure:
'
gg
s
I
M
K =
Igg’: moment d’inertie par rapport à gg’.
( ) ( )
[ ]
3
3
)
)(
( h
y
b
b
by −
−
−
( ) ( )
[ ]
2
1
2
1
3
0
1
0
3
1
' '
15
3
)
)(
(
y
d
A
d
y
A
h
y
b
b
by
I st
sc
gg −
+
−
+
−
−
−
=
( )
−
=
−
=
=
)
(
15
'
15
1
1
1
y
d
K
d
y
K
Ky
st
sc
b
σ
σ
σ](https://image.slidesharecdn.com/coursbael-230209200545-b344fe2d/85/Cours_BAEL-pdf-228-320.jpg)




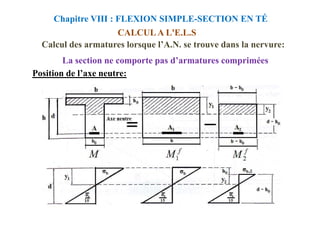




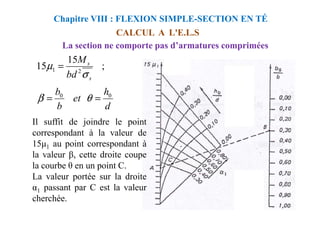


![CALCUL A L'E.L.S
Chapitre VIII : FLEXION SIMPLE-SECTION EN TÉ
La section ne comporte pas d’armatures comprimées
( ) ( )
[ ] )
1
(
2
.
2
.
1
0
1
0
0
2
1
0
y
Z
h
y
h
b
b
y
b
M
Z
F
M b
s
b
s
σ
−
−
+
=
⇒
=
On pose:
d
y
et
d
h
b
b
bd
Ms
1
1
0
0
2
1 ;
; α
θ
β
σ
µ =
=
=
=
On a:
d
y
et
d
b
bd s
1
1
2
1 ;
; α
θ
β
σ
µ =
=
=
=
( )
1
1
1
1
15
α
α
σ
σ −
=
=
b
s
k
( )
( ) ( )
( )
( )( )2
1
2
1
1
1
1
2
1
1
1
1
1
30
2
1
1
30
θ
α
β
α
α
µ
θ
α
θ
β
βα
α
µ
−
−
−
−
=
−
−
+
−
=
d
d
Z
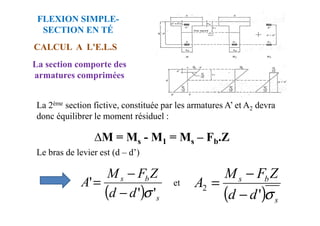
On remplace Ms, b0/b, h0/d, y1 et σs/σb dans (1):](https://image.slidesharecdn.com/coursbael-230209200545-b344fe2d/85/Cours_BAEL-pdf-242-320.jpg)







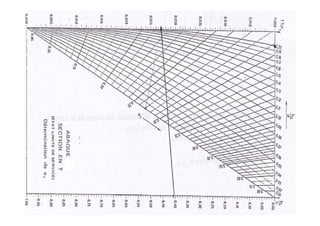
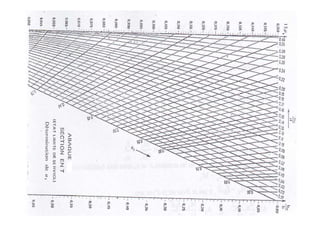
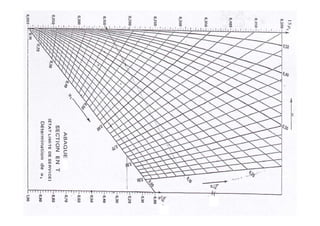































![Σyds représente le moment statique par rapport à gg’ de la section
homogène.
Σ
FLEXI0N COMPOSÉE-
section rectangulaire
Section entièrement comprimée
Etat Limite de Service
Conditions à remplir
Comme G est le centre de gravité de la section, alors Σyds=0
d’où:
( )
[ ]
2
1 '
'
15
' A
A
B
GG
N
N
N s
i
e +
+
=
⇒
=
( )
2
1 '
'
15
'
A
A
B
N
GG s
+
+
=
⇒](https://image.slidesharecdn.com/coursbael-230209200545-b344fe2d/85/Cours_BAEL-pdf-285-320.jpg)


![FLEXI0N COMPOSÉE-
section rectangulaire
Section entièrement comprimée
Etat Limite de Service
Considérons la fibre inférieure de la section, soit v2 la distance de
cette fibre à l’axe gg’ (y2=-v2<0 puisque la fibre est au dessous de
gg’), la contrainte σb,2 a pour valeur:
2
/G
S
s v
M
N
−
=
σ
Conditions à remplir
Pour que la section soit entièrement comprimée en ELS, il faut
que σb,2 soit un effort de compression, donc:
( ) '
2
/
2
1
2
,
'
'
15 gg
G
S
s
b
I
v
M
A
A
B
N
−
+
+
=
σ
0
2
, ≥
b
σ
( )
[ ] 2
2
1
'
/
'
'
15 v
A
A
B
I
N
M gg
S
G
S
+
+
≤](https://image.slidesharecdn.com/coursbael-230209200545-b344fe2d/85/Cours_BAEL-pdf-288-320.jpg)
![En outre l’effort normal Ns doit être un effort de compression.
Par conséquent, pour qu’une section soumise à la flexion composée
soit entièrement comprimée à l’E.L.S., il faut que:
FLEXI0N COMPOSÉE-
section rectangulaire
Section entièrement comprimée
Etat Limite de Service
Conditions à remplir
soit entièrement comprimée à l’E.L.S., il faut que:
L’effort normal Ns soit un effort de compression,
L’inégalité suivante soit vérifiée:
( )
[ ] 2
2
1
'
/
'
'
15 v
A
A
B
I
N
M gg
S
G
S
+
+
≤
Reste à calculer Igg’ et v2.](https://image.slidesharecdn.com/coursbael-230209200545-b344fe2d/85/Cours_BAEL-pdf-289-320.jpg)
![Dans une section rectangulaire entièrement comprimée, on a: B=b.h.
La position du centre de gravité de la section homogénéisée (par
rapport à la fibre supérieure de la section) est définie par:
²
bh
FLEXI0N COMPOSÉE-
section rectangulaire
Section entièrement comprimée
Etat Limite de Service
Conditions à remplir
(Le moment d’inertie par rapport à l’axe gg’)
( )
( ) 1
2
2
1
2
1
1
'
'
15
'
'
'
15
2
²
v
h
v
et
A
A
bh
d
A
d
A
bh
ds
yds
v −
=
+
+
+
+
=
=
∑
∑
( ) ( ) ( )
[ ]
2
1
2
2
1
1
3
2
3
1
' '
'
'
15
3
v
d
A
d
v
A
v
v
b
Igg −
+
−
+
+
=](https://image.slidesharecdn.com/coursbael-230209200545-b344fe2d/85/Cours_BAEL-pdf-290-320.jpg)



![En remplaçant K , y1 et d’ en fonction de σb,1, σb,2 et δ1 on aura:
( )
( )
2
,
1
,
1
,
1
1
,
'
15
'
15
σ
σ
σ
σ b
b
b
S
h
d
Kd
Ky
−
−
=
−
=
FLEXI0N COMPOSÉE-
section rectangulaire
Section entièrement comprimée
Etat Limite de Service
Calcul des Armatures
( )
[ ]
1
2
,
1
,
1
,
1
, 15 δ
σ
σ
σ
σ b
b
b
S
h
−
−
=
⇒
( )
[ ]
( )
( )
[ ]
1
2
,
1
,
2
,
2
,
2
,
1
,
2
,
1
2
,
15
'
15
'
15
δ
σ
σ
σ
σ
σ
σ
σ
σ
b
b
b
S
b
b
b
S
h
d
Kd
h
y
K
−
+
=
⇒
−
+
=
+
−
=](https://image.slidesharecdn.com/coursbael-230209200545-b344fe2d/85/Cours_BAEL-pdf-294-320.jpg)
![FLEXI0N COMPOSÉE-
section rectangulaire
Section entièrement comprimée
Etat Limite de Service
( ) ( )
( ) ( ) ( )
'
2
'
'
'
2
'
2
'
'
1
,
1
2
2
,
1
,
,
2
,
d
h
A
d
u
bh
M
d
h
F
d
u
F
M
S
b
b
i
a
s
b
i
a
−
+
−
+
=
⇒
−
+
−
=
σ
σ
σ
Calcul des Armatures
On pose:
En remplaçant u2, σ’s,1 et d’ en fonction de σb,1, σb,2 et δ1, on aura:
2
1
,
1
2
, S
i
a
( ) ( )
[ ]
( )
[ ]( ) )
1
(
0
2
1
1
'
15
3
1
3
2
6
²
1
2
,
1
1
,
1
1
2
,
1
1
,
1
,
=
−
+
−
−
−
+
−
−
δ
σ
δ
σ
δ
σ
δ
σ
δ
b
b
b
b
i
a
h
A
bh
M
1
,
2
,
1
1
1
,
,
1
100
'
'
;
²
'
b
b
b
i
a
et
bh
A
bh
M
σ
σ
λ
ρ
σ
µ =
=
=
( )
[ ]
( )
1
2
,
1
,
1
,
1
, 15 δ
σ
σ
σ
σ b
b
b
S −
−
=
( )
( )
+
+
=
1
,
2
,
1
,
2
,
2
3
2
b
b
b
b
h
u
σ
σ
σ
σ](https://image.slidesharecdn.com/coursbael-230209200545-b344fe2d/85/Cours_BAEL-pdf-295-320.jpg)
![FLEXI0N COMPOSÉE-
section rectangulaire
Section entièrement comprimée
Etat Limite de Service
( ) ( )
3
1
3
2
6
²
)
1
(
1
,
2
,
1
1
,
1
,
1
2
1
,
2
,
−
+
−
−
⇒
σ
σ
δ
σ
σ
δ
σ b
b
b
b
b
i
a
bh
bh
bh
M
1
1
1
,
,
1
100
'
'
²
'
b
i
a
bh
A
bh
M
σ
ρ
σ
µ
=
=
Calcul des Armatures
( )
[ ] ( )( ) 0
2
1
1
'
15
,
0
3
1
3
2
6
1
' 1
1
1
1
1
1
1 =
−
+
−
−
−
+
−
−
⇒ δ
λ
δ
δ
ρ
λ
δ
δ
µ
( )
[ ]
( )( )
1
1
1
1
1
1
1
2
1
1
90
,
0
3
1
3
2
'
6
'
δ
λ
δ
δ
λ
δ
δ
µ
ρ
−
+
−
−
+
−
−
=
( ) ( ) 0
2
1
1
'
15 1
1
,
2
,
1
1
,
1
,
1
2
1
1
,
1
,
1
,
=
−
+
−
−
δ
σ
σ
δ
σ
σ
δ
b
b
b
b
b
b
b
bh
h
A 1
,
2
,
b
b
σ
σ
λ =](https://image.slidesharecdn.com/coursbael-230209200545-b344fe2d/85/Cours_BAEL-pdf-296-320.jpg)
![En remplaçant u , σ’ et d’ en fonction de σ , σ et δ , on aura
Écrivons le moment par rapport aux armatures supérieures:
( ) ( ) 0
'
2
'
1
, =
−
+
−
+ d
h
F
d
u
F
M s
b
s
a
FLEXI0N COMPOSÉE-
section rectangulaire
Section entièrement comprimée
Etat Limite de Service
Calcul des Armatures
En remplaçant u1, σ’s,2 et d’ en fonction de σb,1, σb,2 et δ1, on aura
( ) ( )
[ ]
( )
[ ]( ) 0
2
1
1
'
15
3
1
3
2
6
²
1
1
,
1
2
,
1
2
1
,
1
2
,
1
,
=
−
+
−
+
−
+
−
+
δ
σ
δ
σ
δ
σ
δ
σ
δ
b
b
b
b
s
a
h
A
bh
M
1
,
2
,
2
2
1
,
,
2
100
'
'
;
²
'
b
b
b
s
a
et
bh
A
bh
M
σ
σ
λ
ρ
σ
µ =
=
=
On pose:](https://image.slidesharecdn.com/coursbael-230209200545-b344fe2d/85/Cours_BAEL-pdf-297-320.jpg)
![De la même façon on obtient:
( )
[ ] ( )
[ ]( ) 0
2
1
1
'
15
,
0
3
1
3
2
1
' 1
1
1
2
1
1
2 =
−
+
−
+
−
+
−
+ δ
δ
λ
δ
ρ
δ
λ
δ
µ
FLEXI0N COMPOSÉE-
section rectangulaire
Section entièrement comprimée
Etat Limite de Service
Calcul des Armatures
( )
[ ] ( )
[ ]( ) 0
2
1
1
'
15
,
0
3
1
3
2
6
' 1
1
1
2
1
1
2 =
−
+
−
+
−
+
−
+ δ
δ
λ
δ
ρ
δ
λ
δ
µ
( )
[ ]
( )
[ ]( )
1
1
1
1
1
2
2
2
1
1
90
,
0
3
1
3
2
'
6
'
δ
δ
λ
δ
δ
λ
δ
µ
ρ
−
+
−
−
+
−
−
−
=
( )
( )( ) 1
2
1
1
2
1
1
2
1
3
2
'
2
1
1
9
,
0
'
2
1
9
,
0
1
'
6
3
δ
ρ
δ
δ
ρ
δ
δ
µ
δ
λ
−
+
−
−
−
−
−
−
=
et:](https://image.slidesharecdn.com/coursbael-230209200545-b344fe2d/85/Cours_BAEL-pdf-298-320.jpg)

![( )
( )( ) 1
2
1
1
2
1
1
2
1
3
2
'
2
1
1
9
,
0
'
2
1
9
,
0
1
'
6
3
δ
ρ
δ
δ
ρ
δ
δ
µ
δ
λ
−
+
−
−
−
−
−
−
=
FLEXI0N COMPOSÉE-
section rectangulaire
Section entièrement comprimée
Etat Limite de Service
Calcul des Armatures
( )
[ ]
( )( )
1
1
1
1
1
1
1
2
1
1
90
,
0
3
1
3
2
'
6
'
δ
λ
δ
δ
λ
δ
δ
µ
ρ
−
+
−
−
+
−
−
=
100
'
' 1
1
bh
A ρ
=](https://image.slidesharecdn.com/coursbael-230209200545-b344fe2d/85/Cours_BAEL-pdf-300-320.jpg)

![Posons:
h
N
M
et
N
bh
h
d
bh
A
s
G
s
b /
1
6
;
'
;
100
=
=
=
= ε
σ
υ
δ
ρ
FLEXI0N COMPOSÉE-
section rectangulaire
Section entièrement comprimée
Etat Limite de Service
Calcul des Armatures
Soit :
s
s
( )2
1
2
1
9
,
0
1
30
,
0
1
1
)
2
(
δ
ρ
ε
ρ
υ
−
+
+
+
=
⇒
( ) ( )( )
[ ]
( ) 0
1
2
1
1
3
30
,
0
2
1
27
,
0
2
1
2
2
1
=
−
+
−
−
−
+
−
+
−
υ
ε
ρ
δ
υ
ε
υ
ρ
δ
υ](https://image.slidesharecdn.com/coursbael-230209200545-b344fe2d/85/Cours_BAEL-pdf-302-320.jpg)
![FLEXI0N COMPOSÉE-
section rectangulaire
Section entièrement comprimée
Etat Limite de Service
On prend:
( )2
1
2
1
27
,
0 δ
υ −
=
C
( )( )
[ ]
2
1
2
1
1
3
15
,
0 δ
υ
ε
υ −
−
+
−
=
D
Calcul des Armatures
L’équation devient:
La racine positive:
[ ]
1
υ
ε −
+
=1
E
0
2
2
=
−
+ E
D
C ρ
ρ
C
EC
D
D +
+
−
=
2
ρ
100
bh
A
ρ
=](https://image.slidesharecdn.com/coursbael-230209200545-b344fe2d/85/Cours_BAEL-pdf-303-320.jpg)
![On calcule:
On déduit:
En résumé:
h
d
h
N
M
N
bh
s
G
s
b '
;
6
; 1 =
=
= δ
ε
σ
υ
( ) ( )( )
[ ]
2
2
2
1
1
3
15
,
0
;
2
1
27
,
0 δ
υ
ε
υ
δ
υ −
−
+
−
=
−
= D
C
FLEXI0N COMPOSÉE-
section rectangulaire
Section entièrement comprimée
Etat Limite de Service
Calcul des Armatures
On a:
Et enfin:
( ) ( )( )
[ ]
2
1
2
1 2
1
1
3
15
,
0
;
2
1
27
,
0 δ
υ
ε
υ
δ
υ −
−
+
−
=
−
= D
C
υ
ε −
+
=1
E
C
EC
D
D +
+
−
=
2
ρ
100
bh
A
ρ
=](https://image.slidesharecdn.com/coursbael-230209200545-b344fe2d/85/Cours_BAEL-pdf-304-320.jpg)
![Calcul des contraintes
On a: ( )
2
1
0 '
'
15 A
A
bh
B +
+
=
bh2
1
FLEXI0N COMPOSÉE-
section rectangulaire
Section entièrement comprimée
Etat Limite de Service
et
On déduit:
( )
+
+
= d
A
d
A
bh
B
v 2
1
2
0
1 '
'
'
15
2
1
1
2 v
h
v −
=
( ) ( ) ( )
[ ]
2
1
2
2
1
1
3
2
3
1
' '
'
'
15
3
v
d
A
d
v
A
v
v
b
Igg −
+
−
+
+
=](https://image.slidesharecdn.com/coursbael-230209200545-b344fe2d/85/Cours_BAEL-pdf-305-320.jpg)
![Donc :
On a:
'
0
0 '
gg
G
I
M
K
et
B
N
GG =
=
=
σ
1
0
1
, Kv
b +
= σ
σ
FLEXI0N COMPOSÉE-
section rectangulaire
Section entièrement comprimée
Etat Limite de Service
Calcul des contraintes
1
0
1
, Kv
b +
= σ
σ
2
0
2
, Kv
b −
= σ
σ
( )
[ ]
'
15 1
0
1
, d
v
K
S −
+
= σ
σ
( )
[ ]
1
0
2
, 15 v
d
K
S −
−
= σ
σ](https://image.slidesharecdn.com/coursbael-230209200545-b344fe2d/85/Cours_BAEL-pdf-306-320.jpg)















![On a: yser est la distance entre l’axe
Neutre et la fibre la plus comprimée,
donc: yser=yc+C
FLEXI0N COMPOSÉE-
section rectangulaire
Section partiellement comprimée
Etat Limite de Service
Calcul des contraintes
donc: yser=yc+C
Aussi on a le moment Ms par rapport au
CDG de la section rectangulaire :
Ms=Ns.hg=Ns[ea-(d-h/2)]
donc: )
2
(
h
d
N
M
e
s
s
a −
+
=](https://image.slidesharecdn.com/coursbael-230209200545-b344fe2d/85/Cours_BAEL-pdf-322-320.jpg)



![On a:
(yser=yc+C)
( ) ( )
[ ]
2
2
3
'
'
15
3
d
y
A
y
d
A
by
I ser
ser
ser
−
+
−
+
=
FLEXI0N COMPOSÉE-
section rectangulaire
Section partiellement comprimée
Etat Limite de Service
Calcul des contraintes
On pose:
Alors:
et
avec:
(yser=yc+C)
3
S
N
K = ( ) ( )
[ ]
ser
ser
ser
y
d
A
d
y
A
by
S −
−
−
+
= '
'
15
2
b
ser
b Ky σ
σ ≤
= ( ) s
ser
s y
d
K σ
σ ≤
−
=15](https://image.slidesharecdn.com/coursbael-230209200545-b344fe2d/85/Cours_BAEL-pdf-326-320.jpg)










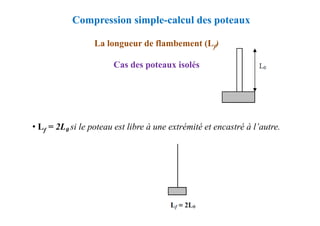
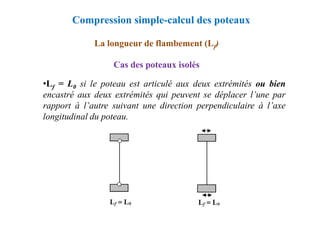
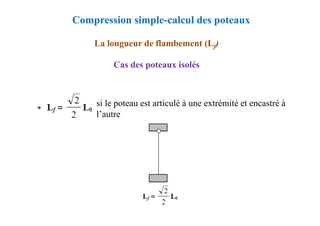






















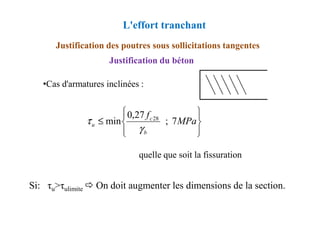


![Conditions complémentaires
Espacement St des cours d’armature
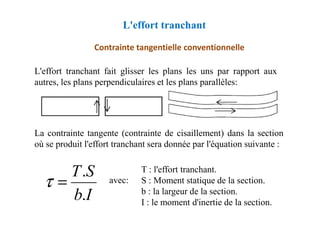
Justification des poutres sous sollicitations tangentes
L'effort tranchant
St ≤ min [0,9d ; 40 cm]
Section minimale d’armature transversale
MPa
S
b
f
A
t
e
t
4
,
0
.
.
≥](https://image.slidesharecdn.com/coursbael-230209200545-b344fe2d/85/Cours_BAEL-pdf-372-320.jpg)
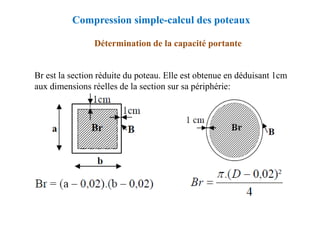
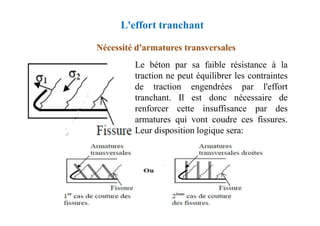
![Dimension des armatures transversales
∅ ∅
Justification des poutres sous sollicitations tangentes
Conditions complémentaires
L'effort tranchant
∅t ≤ min [h/35 ; ∅l ; b/10]
∅t : diamètre des armatures transversales
∅l : diamètre des armatures longitudinales
h : hauteur totale de la poutre
b : largeur de la poutre](https://image.slidesharecdn.com/coursbael-230209200545-b344fe2d/85/Cours_BAEL-pdf-373-320.jpg)



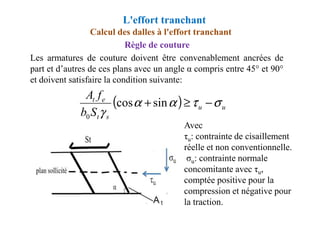

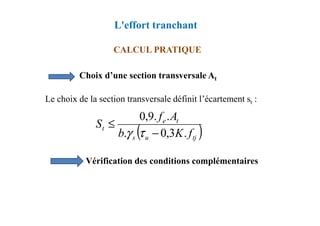
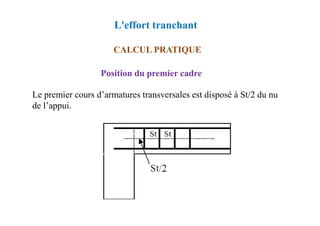


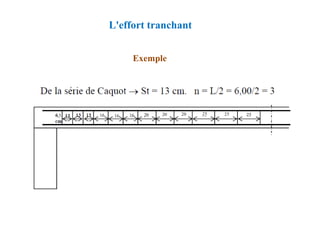
































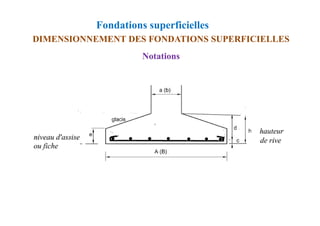











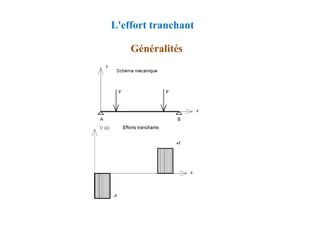
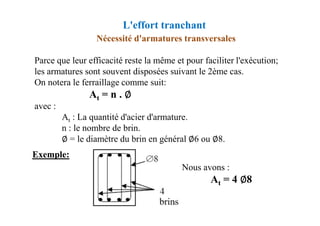
![Chapitre XIII: Fondations superficielles
DIMENSIONNEMENT DES FONDATIONS SUPERFICIELLES
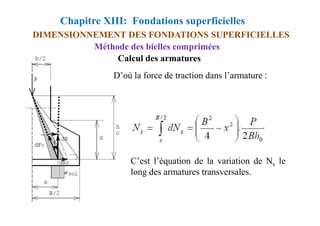
La contrainte limite de traction dans l’acier
étant σs, la section d’armatures
transversales par mètre de semelle est donc
:
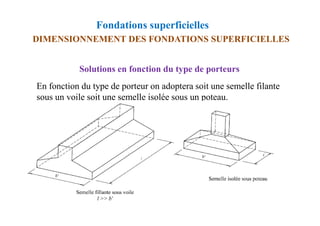
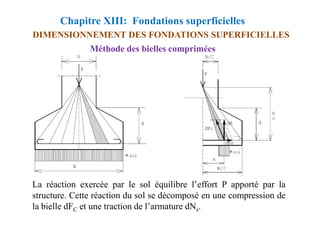
Méthode des bielles comprimées
Calcul des armatures
:
Triangle OMC h0/d=(B/2)/[(B-b)/2]
donc:](https://image.slidesharecdn.com/coursbael-230209200545-b344fe2d/85/Cours_BAEL-pdf-438-320.jpg)




















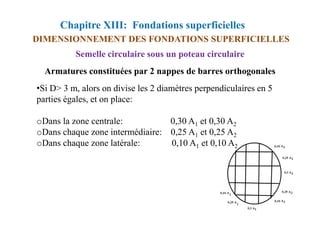


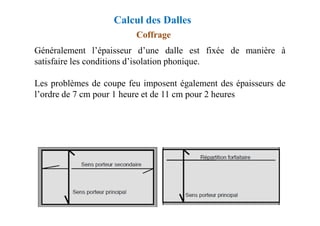
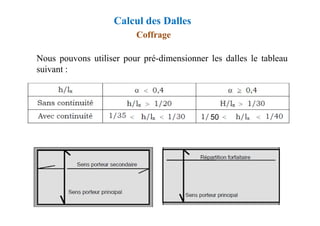










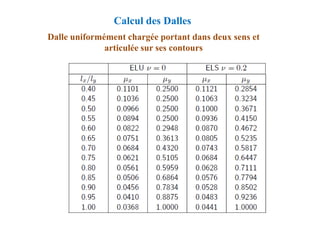
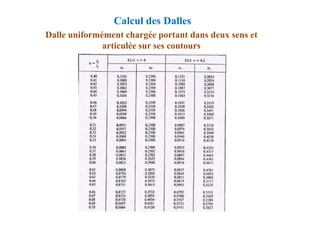
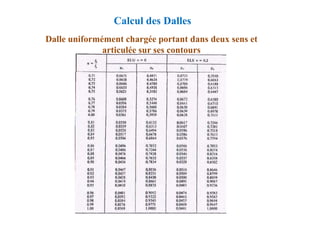





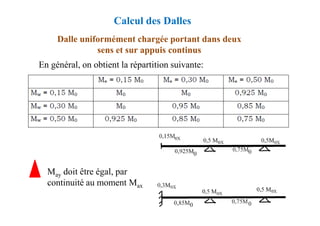

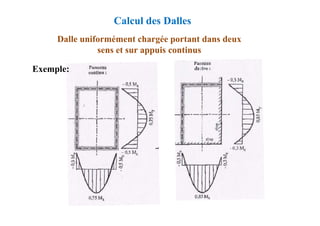











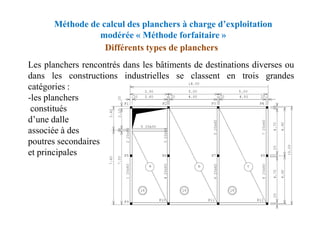












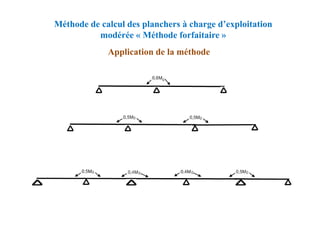
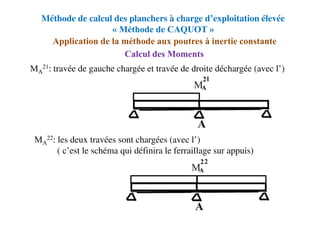
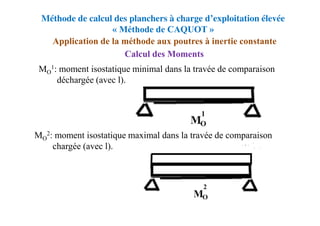
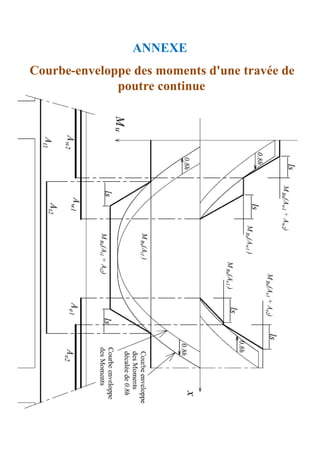
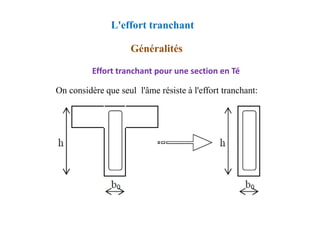
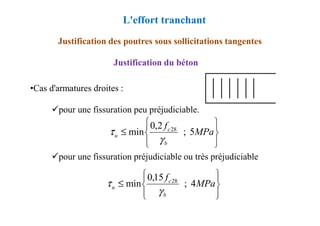
![Méthode de calcul des planchers à charge d’exploitation
modérée « Méthode forfaitaire »
Application de la méthode
Les valeurs de Mt, Mw et Me doivent vérifier les conditions
suivantes :
( )
[ ]
0
0 3
,
0
1
;
05
,
1
2
.
1 M
M
Max
M
M
M e
w
t α
+
≥
+
+ ( )
[ ]
0
0 3
,
0
1
;
05
,
1
2
.
1 M
M
Max
Mt α
+
≥
+
0
2
3
,
0
1
.
2 M
Mt
α
+
≥
0
2
3
,
0
2
,
1
M
Mt
α
+
≥
dans le cas d’une travée intermédiaire,
dans le cas d’une travée de rive.](https://image.slidesharecdn.com/coursbael-230209200545-b344fe2d/85/Cours_BAEL-pdf-512-320.jpg)