Le document traite des poutres en flexion simple sous l'état limite ultime, en expliquant les hypothèses de calcul et les caractéristiques des sections, y compris les sections rectangulaires sans et avec armature comprimée ainsi que les sections en T. Il détaille également les diagrammes de calcul pour les matériaux (béton et acier) et les méthodes de dimensionnement en fonction des déformations et des sollicitations. Les principes de résistance, d'adhérence entre béton et acier, ainsi que les conditions de calcul et les précautions à prendre sont également abordés.

1. 1
Chapitre V
Poutre en flexion simple – Etat Limite Ultime ELU
1. Introduction
2. Hypothèses de calcul
3. Section rectangulaire sans armature comprimée
4. Section rectangulaire avec armature comprimée
5. Section en T
6. Divers

2. 2
M. SADEK
 Poutre noyée
 Poutre avec retombée
 Poutre avec rehausse
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

3. 3
M. SADEK
 Poutre sollicitée en flexion simple : M(x), V(x)
Note : en Béton Armé, les effets de ces deux sollicitations sont traités séparément.
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

4. 4
M. SADEK
 Flexion simple / pure
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

5. 5
 Apparition des premières fissures
 Accentuation des fissures
 Allongement excessif de l’acier / écrasement du béton
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

6. 6
M. SADEK
 Poutre sollicitée en flexion simple (ELU)
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

7. 7
HYPOTHÈSES
H1) Principe de Navier-Bernoulli : au cours des déformations, les
sections droites restent planes et conservent leurs dimensions (Champ
de déformation linéaire dans la section)
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

8. 8
HYPOTHÈSES
H2) La résistance du béton tendu est négligée
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

9. 9
HYPOTHÈSES
H3) un groupe de barres disposées en plusieurs lits est
équivalent à une barre unique située au C.D.G du groupe.
H4) Pas de glissement relatif entre acier et béton - Adhérence
parfaite entre l’acier et le béton :
au contact entre le béton et les armatures : s=c
H5) Les diagrammes de calcul contrainte-déformation pour le
béton et l'acier sont :
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

10. 10
Béton – diagramme pour le calcul des sections
a) Parabole-rectangle
b) Bilinéaire simplifié
fcd :valeur de calcul de la résistance à la compression sur cylindre (t28j)
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

11. 11
c) Rectangulaire simplifié
Note : Dans notre calcul des sections à l’ELU, on adoptera le diagramme c.
L’utilisation des diagrammes a et b est autorisée par le code, voir annexe
pour le coefficient de remplissage et la position du CDG.
cc= 1 (ANF)
C = 1.5 (Situation durable) ; 1.2 (accidentelle)
Béton – diagramme pour le Calcul des sections
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

12. 12
 Diagrammes de calcul :
 Branche sup. horizontale (sans limitation de la déformation de l’acier)
 Branche sup. inclinée (s  ud) ,
s = 1.15 (durable)
1.0 (accidentelle)
Acier – diagrammes pour le Calcul des sections
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

13. 13
Exemple : Cas durable : fyd = fyk / s = 435 MPa
se = fyd/Es = 2.17.10-3
 < se => s = 200 000 
 > se => s = 435 MPa.
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

14. 14
 s > se (situation durable)
s  435 + 727 (s -2.17.10-3) < 466 MPa pour les aciers B
s  435 + 952 ( s -2.17.10-3) < 454 MPa pour les aciers A
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

15. 15
Règle de 3 Pivots :
Le dimensionnement à l’ELU se fait en supposant que le diagramme des
déformations passe par l’un des trois Pivots A, B ou C
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

16. 16
 Pivot A (peu fréquent)
 Acier : c  cu
s = ud dépend du type d’acier (A, B ou C)
(pas de limitation si diagramme à palier horizontal)
Différence avec le BAEL : L’EC2 ne retient plus un pivot A à 10x10-3 mais à ud
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

17. 17
 Pivot B (Cas courant)
 Béton : c = cu2 =3.5 ‰ , c2 =2 ‰ (pour fck50 MPa)
s  ud
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

18. 18
Pivot C
(h-y) / h = c2/cu2 => y = (1-c2/cu2).h
(Compression, flexion composée)
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

19. 19
Flexion simple, ELU
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

20. 20
 Combinaison fondamentale (Détail - Ch. 2)
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

21. 21
c
s
sc
Diagramme de
Déformations Efforts internes
Fc,sc
Fsc
Fc
Fs
z
 A : aire des armatures tendues
 d : hauteur utile - distance du centre de gravite des armatures tendues As à la fibre la plus comprimée
 A’ : aire des armatures comprimées éventuelles
 d’ : distance du centre de gravite de A’ à la fibre de béton la plus comprimée
 z : bras de levier
M > 0
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

22. 22
 Fc : résultante des efforts de compression dans le béton
 Fsc : résultante des efforts de compression dans les aciers comprimés
 Fc,sc : résultante de Fc et Fsc
 Fs : résultante des efforts de traction dans les armatures tendues
 x : position de l’Axe Neutre
c
s
sc
Diagramme de
Déformations Efforts internes
x Fc,sc
Fsc
Fc
Fs
z
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

23. 23
c
s
sc
Diagramme de
Déformations Efforts internes
x Fc,sc
Fsc
Fc
Fs
z
 Equilibre des forces Fs = Fc,sc
 Equilibre des moments MEd = Fc,sc .z = Fs.z
 3 Inconnus (en général) : A, A’, x
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

24. 24
Section rectangulaire, sans armature comprimée (A’=0)
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

25. 25
Section rectangulaire, sans armature comprimée (A’=0)
Simplification de la loi de
comportement de l’acier
EC2 3.1.7(3)
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

26. 26
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

27. 27
Fc
FS
Fc = Fs
MED = Fc.z
z
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

28. 28
 Ecriture adimensionnelle :
On pose :
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

29. 29
 fck 50 MPa,  = 1 ; =0.8
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

30. 30
On note que :
x = u.d =(c / c+s) d
u = (c / c+s)
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

31. 31
 Frontières des pivots A, B
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

32. 32
 Frontières des pivots A, B
 Acier type A  ud = 22,5 .10-3  AB = (3.5 / 3.5+22.5) = 0.135  AB = 0.102
 Acier type B   AB =0.072  AB = 0.056
 Acier type C   AB =0.049  AB = 0.039
 fck  50 MPa,  = 1 ; =0.8
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

33. 33
 Pivot B AB  u
En général, on constate que l’on est pratiquement toujours en pivot B
 c = cu2 =3.5 ‰ ; s  ud
 s = (1/u -1) cu
(on fait travailler le béton au max)
 Frontières des pivots A, B
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

34. 34
 Pivot B AB  u  lim
 Il ne faut pas avoir un acier sur le palier élastique, si non l’acier sera mal utilisé !
Dans ce cas, il faudra soit diminuer la section d’acier, soit prévoir une armature
comprimée pour mobilier un moment résistant plus élevé.
 Frontières des pivots A, B
s  ud mais s  se
Droite BE (section de poutre en
Pivot B et acier à la limite élastique)
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

35. 35
 Frontières des pivots A, B
(fck  50 Mpa)
Combinaisons Durables Combinaisons Accidentelles
s = 1.15 s = 1
fyk(MPa) lim lim lim lim
400 0.668 0.392 0.636 0.380
500 0.617 0.372 0.583 0.358
lim = BE
 Pivot B AB  u  lim
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

36. 36
 Frontières des pivots A, B
 Pivot A
s =ud ; c =cu
u  AB
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

37. 37
 Calcul de l’armature tendue A (fck 50 MPa)
a) Diagramme à palier incliné
i. u  AB  Pivot A
s = 454 MPa (Acier A) , 466 MPa (acier B)
ii. AB  u  lim  Pivot B
s = (1/u -1) cu
s  435 + 727 (s -2.17.10-3) < 466 MPa pour les aciers B
s  435 + 952 (s -2.17.10-3) < 454 MPa pour les aciers A
(A’=0, u  lim )
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

38. 38
 Calcul de l’armature tendue A (fck 50 MPa)
b) Diagramme à palier horizontal
(A’=0, u  lim )
s = fyd
Note : Pas de limitation pour la déformation de l’acier
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

39. 39
Note 1
 Hauteur utile d – valeur initiale de calcul
 d ne peut pas être déterminé exactement avant le calcul et le choix de l’armature
 prendre d  0.9 h pour les poutres courantes (formule trop favorable pour les poutres
noyées et les dalles d’épaisseur  20 cm)
 prendre d = h – cnom – 1 cm (dalle d’épaisseur  20 cm )
 Après détermination de l’armature, il est possible de calculer précisément la
hauteur utile dréel. Si dréel est nettement différente de dinitial , il peut être judicieux de
recalculer As.
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

40. 40
 Note 2
 Formule approchée pour le calcul de A
(pour vérifier l’ordre de grandeur)
z  0.9d ; d  0.9 h
 Avec cette formule approchée, aucune information n’est donnée sur la
contrainte de compression du béton. Elle sera complètement erronée si une
armature comprimée est nécessaire.
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

41. 41
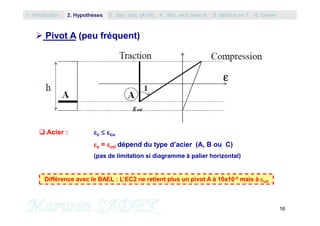
 Armature de fragilité
 Pour une section rectangulaire bh, le moment résistant ultime du béton non armé
MRc = (I/v)  fctm = (b.h²/6)  fctm
 La section As,min équilibre un moment
MRs = As,min  fyk  z
 En considérant MRc = MRs , et en remplaçant z  0.9 d ; h d / 0.9
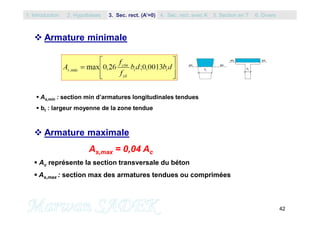
As,min = b.d.[fctm/(0.9  0.81  6)fyk]  0.23 b d fctm / fyk
 L’EC2 remplace la valeur 0.23 par 0.26 et borne inférieurement la quantité 0.26
fctm/fyk à la valeur 0.0013
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

42. 42
 Armature minimale
 Armature maximale
As,max = 0,04 Ac
 Ac représente la section transversale du béton
 As,max : section max des armatures tendues ou comprimées
 As,min : section min d’armatures longitudinales tendues
 bt : largeur moyenne de la zone tendue
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

43. 43
Section rectangulaire, avec armature comprimée (A’0)
u  lim
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

44. 44
Section rectangulaire, avec armature comprimée (A’0)
 3 inconnues (A, A’, x) / 2 équations ???
 Infinité de solutions
 Possibilité n°1 : Minimum de " A+ A’ " (calcul long)
 Possibilité n°2 : Notion de moment limite (adoptée en général)
Résolution par la Méthode de décomposition en 2 sections fictives
u  lim
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

45. 45
2 sections fictives
 On fait travailler le béton au max sous Mlim  A1
 L’armature comprimée A’ reprend (Med  Mlim)  A2
u  lim  Med  Mlim= lim .b.d².fcd
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

46. 46
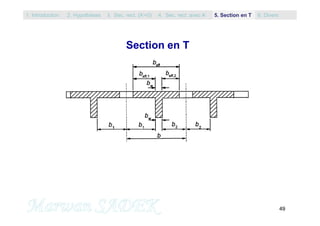
cu
s
sc
x=lim.d
d’
d
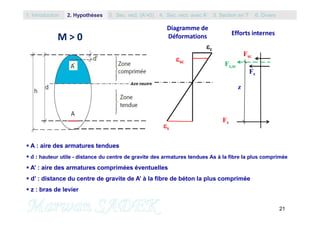
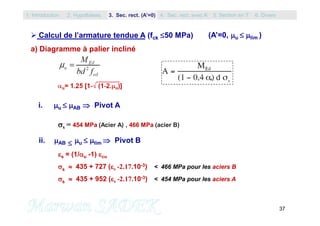
A1 = Mlim / (1 – 0.4.lim).d.fyd
A’ = (Med – Mlim) / [sc . (d-d’)]
sc = 3,5.10-3. (1-d’/xlim)
La valeur de sc est proche de 3 °/°° (>se), qui donne une valeur de sc=fyd avec le
diagramme à palier horizontal et une valeur légèrement supérieur à fyd avec le
diagramme à palier incliné. Dans tous les cas, on pourra retenir une valeur de sc=fyd .
A2 = A’. sc / s = A’. fyd/ s
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

47. 47
A1 = Mlim / [(1 – 0.4.lim).d.fyd]
A2 = A’. sc / s
A’ = (Med – Mlim) / [fyd . (d-d’)]
 Lorsque A et A’ de même type  sc = s = fyd  A2 = A’
A = A1 + A2
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

48. 48
 Note 1 : l’EC2 ne limite plus le moment repris par l’armature
comprimée comme dans le BAEL (40% Med). Cependant, elle sera bornée
par la valeur de
A+A’  As,max = 0,04 Ac
 Note 2 : Il convient de maintenir toute armature longitudinale
comprimée (de diamètre ) prise en compte dans le calcul de résistance
au moyen d'armatures transversales espacées au plus de 15 
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

49. 49
Section en T
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

50. 50
 Largeur participante des tables de compression
 l0 : distance entre points de moment nul
(EC 2-1-1, 5.3.2)
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

51. 51
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers
 Largeur participante des tables de compression

52. 52
(EC 2-1-1, 5.3.2)
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers
 Largeur participante des tables de compression

53. 53
 Moment maximum repris par la poutre dans le cas où la
table travaille entièrement en compression
2
f
uT eff f cd
h
M b h f (d ) 
1sA
ux fh
s 1sN
1cN
 ff h,dz 501
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

54. 54
1er cas: cas fréquent M Mu uT
bw
b = beff
d
hf
L’axe neutre est situé dans la table de
compression, seule une partie de la table est
comprimée
la section en T se calcule comme une section
rectangulaire de largeur beff et de hauteur h
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

55. 55
2ème cas: L’axe neutre est situé dans la nervureM Mu uT
Décomposition en 2 sections fictives
Il faut s’attendre à une section d’armatures très importante
bw
b=beff
d
hf
=
beff-bw
A1
A2
bw
+
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

56. 56
M Mu uT
1
eff w
u uT
eff
b b
M M
b

 Section A1 va résister :
bw
b=beff
d
hf
=
beff-bw
A1
A2
bw
+
A1= (beff-bw)×h0×fcd / s
(s = fyd, si diagramme à
palier horizontal)
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

57. 57
M Mu uT
 Section A2 va résister
 Calcul comme section rectangulaire de largeur bw et de hauteur h
bw
b=beff
d
hf
=
beff-bw
A1
A2
bw
+
M M Mu u u2 1 
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

58. 58
M Mu uT
 s = fyd , si diagramme à palier horizontal ou Pivot A (palier incliné)
 s = à déterminer en fonction de s si Pivot B (diagramme à palier incliné) ,
cette contrainte pourra être utilisée pour le calcul de A1
cdw
u
u
fdb
M
2
2
2   u u2 2125 1 1 2  , ( )
 Attention : Nécessité de A’ si u2 > lim
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

59. 59
M Mu uT
bw
b=beff
d
hf
=
beff-bw
A1
A2
bw
+
A = A1 + A2
A1= (beff-bw)×h0×fcd / s
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

60. 60
Prédimensionnement – Section rectangulaire (ordre de grandeurs)
b
h
Si b n’est pas imposée on peut prendre
0.3 h  b  0.5 h
On fixe une valeur pour b et on cherche la
valeur de h
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

61. 61
Prédimensionnement – Section rectangulaire (ordre de grandeurs)
b
h
b/h  0.4 ; h  2.5 b
d  0.9 h = 2.25 d
 Pivot B AB  u  lim
 Acier B 0.056  u  0.372
0.056  Med / bd²fcd  0.372
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

62. 62
Prédimensionnement – Section rectangulaire (ordre de grandeurs)
b
h
 Autres critères
- Dimensionnement ELS, flèche
 Acier A
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

63. 63
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

64. 64
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers

65. 65
1. Introduction 3. Sec. rect. (A’=0) 5. Section en T2. Hypothèses 4. Sec. rect. avec A’ 6. Divers
 source :Thonier (2013)

66. 66
M. SADEK
Exercices
 Section rectangulaire sans armature comprimée :
 Calcul de armature tendue
o diagramme avec palier incliné
o Diagramme avec palier horizontal
o Calcul de la valeur exact de d
 Section rectangulaire avec armature comprimée :
 Calcul armature tendue et comprimé
 Prédimensionnement d’une poutre rectangulaire et calcul
d’armature avec prise en compte du poids propre
 Calcul d’une poutre en T