Ce document est un polycopié destiné aux étudiants en licence de génie civil et infrastructures, regroupant des rappels de cours et des exercices sur la résistance des matériaux et le calcul de structures. Il contient des sections sur les bases de la résistance des matériaux, le flambement, les théorèmes énergétiques, et diverses méthodes de calcul pour les poutres et structures isostatiques. En outre, il inclut de nombreux exercices et sujets d'examen pour aider les étudiants à appliquer les concepts appris.



![3. Théorèmes énergétiques
Pour une poutre droite de longueur L sous chargement plan, l’énergie de déformation réelle est :
L 2 2 2
N
W d = 1 ∫ ( + M + T ) dx
2 0 ES EI GS1
Pour une poutre élancée, la contribution de l’effort tranchant à Wd est négligeable devant celle de la flexion.
r r
Le travail réel d’une action mécanique de résultante F , de moment C en P, appliquée à un solide S en mouvement par
rapport au référentiel R est :
r r v v
W e = 1 (U P∈S / R.F + ΩS / R.C)
2
Principe des travaux virtuels (PTV) : Le travail des efforts intérieurs réels (N, M, T) dans un champ de déformation
virtuel (dus aux efforts intérieurs virtuels N*, M*, T*) est égal au travail des efforts extérieurs réels dans le champ de
déplacement virtuel (associé aux déformations virtuelles).
Pour une poutre de longueur L soumise à des forces et moments aux points Pi, le PTV s’écrit :
L
N N * M M * T T* r r* r r*
W d (σ, ε ) = W e(F, U ) ⇔ (
* *
∫ ES
+
EI
+
GS1
)dx = ∑[F .U (P )+ C .Ω (P )]
i
i i i i
0
r
Théorème de la charge unité : Soit v le déplacement en P selon n d’une poutre de longueur L, on applique une force
r
virtuelle d’intensité égale à 1 en P selon n pour déterminer v. Selon le PTV et en négligeant l’effet de T :
L
N N* M M *
v =∫( + ) dx
0
ES EI
* *
N, M efforts intérieurs réels et N , M efforts intérieurs dus à la force +1
4. Méthode des forces – Superposition de problèmes isostatiques
La méthode est illustrée avec l’exemple de problème
F
hyperstatique de degré h (h=2) ci-contre. Ce problème est
équivalent à la superposition de (h+1) problèmes isostatiques
0 1 2
associés à h conditions cinématiques.
L L/2 L/2
Soient X1 et X2 les réactions aux appuis en 1 et 2.
F
= 0 1 2 + 0 1 2 + 0 1 2
X1 X2
problème 0 problème 1 problème 2
Conditions ∆1 = ∆10 + X1 δ11 + X 2 δ12 = 0 ∆i0 flèche en i (i=1,2) dans le pb 0
cinématiques ∆ 2 = ∆ 20 + X1 δ21 + X 2 δ22 = 0 δij flèche en i (i=1,2) dans le pb j pour une force Xi=1
3 3 3 3
Après calculs ou par utilisation d’un formulaire : ∆10 = −12FL
7
EI
, ∆20 = −16EI
27FL , δ11 = 3L , δ22 = 8L ,
EI 3EI
3
δ21 = δ12 = 5L
6EI
d’où X1= 43 F et X2= 11 F
56 28
-4-](https://image.slidesharecdn.com/40872913-formulaire-de-rdm-130204112444-phpapp01/85/40872913-formulaire-de-rdm-4-320.jpg)


![7. Formulaire de flèches de poutres isostatiques
P(L−α) 3 P(L−α)
y 0≤x≤α : y(x) = [x -α(2L-α)x] y'(x) = [3x2- α (2L- α)]
6EIL 6EIL
x α≤x≤L : y(x) = Pα [(L-x)3-(L-α)(L+α)(L-x)]
6EIL
y'(x) = Pα [-3(L-x)2+(L-α)(L+α)]
P 6EIL
2
Pα2(L−α)
y(α) = - pour x=α
3EIL
α L y( L ) = - PL
3
pour x=α= L
2 48EI 2
p p
p y(x) = - (x 4 −2Lx3 + L3x) y'(x) = - (4x 3 −6Lx 2 + L3)
24EI 24EI
5pL4
y( L ) = - pour x= L
2 384 EI 2
y(x) = M (x 3 −3Lx 2 +2L2x) y'(x) = M (3x 2 −6Lx +2L2)
M 6EIL 6EIL
Px 2(x −3α) Px(x −2α)
0≤x≤α : y(x) = y'(x) =
P 6EI 2EI
Pα 2(α−3x)
α≤x≤L : y(x) =
6EI
α L y(L) = - PL3 pour x=α=L
3EI
p p p 3
y(x) = - (x 4 −4Lx3 +6L2x 2) y'(x) = - (x −3Lx 2 +3L2x)
24EI 6EI
pL4
L y(L) = -
8EI
pour x=L
8. Formulaire des réactions de liaison de la poutre bi-encastrée
q
qL qL q 2 −q L2
0
Tij = 0
; Tji = ; M0 = L ; M0 =
ij ji
2 2 12 12
i j
q qa 3 2 3
0
Tij = (1− a ) ; Tji = qa(1− a 2 + a 3)
0
L 2 2L L 2L
i a j qa 2 −qa 3
M0 =
ij ( 2
2 6L −8aL+3a
2
) ; M0 =
ji (4L−3a)
12L 12L2
F − FL
Tij = F ; Tji = F ; M 0 = FL ; M 0 =
0 0
ij ji
2 2 8 8
i L/2 L/2 j
F F Fa(L−a) −Fa(L−a)
Tij = F ; Tji = F ; M 0 =
0 0
ij ; M0 =
ji
L L
i a j
a
F 2 2 2 2
Tij = Fb (b+3a) ; Tji = Fa3 (3b+a) ; M 0 = Fab ; M0 = −Fba
0
3
0
ij 2 ji 2
i j L L L L
a b
C
− 6abC b(2a−b) a(2b−a)
i a b j Tij = 6abC ; Tji =
0 0 ; M0 =
ij C ; M0 =
ji C
L3 L3 L2 L2
-7-](https://image.slidesharecdn.com/40872913-formulaire-de-rdm-130204112444-phpapp01/85/40872913-formulaire-de-rdm-7-320.jpg)





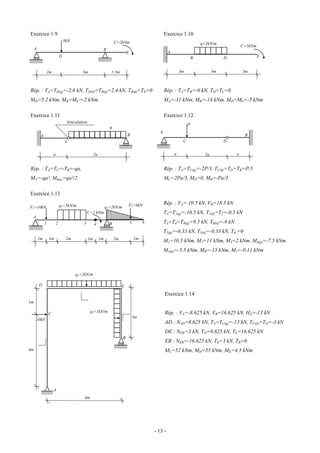





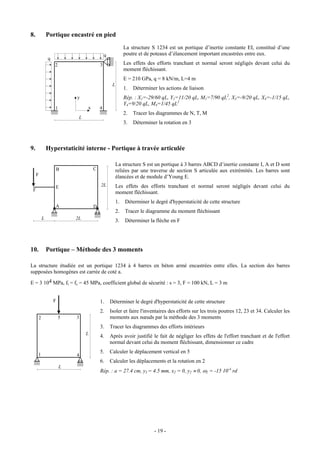

![12. Examen de seconde session 2003
1. Tracer l’allure du moment fléchissant et en préciser les valeurs caractéristiques dans les structures isostatiques
suivantes:
a. Poutre-console q
A B C
L 2L
b. Portique à jambage (barres identiques)
Dans cet exercice on indiquera la valeur du moment fléchissant en C et au milieu E de la traverse [BC].
q
B C
L/2
D
L/2
A
L/2 L
2. Calculer, pour le portique précédent, le déplacement horizontal uc en C.
3. Un appui simple est ajouté en A sur la poutre console précédente, calculer la réaction d’appui en A.
13. Poutres hyperstatiques – Méthode des déplacements
Exercice 12.1 Exercice 12.2.
F F
q q
1 2 3 1 2 3
l1 l2/2 l2/2 l1 l2/2 l2/2
F=60kN, q=18 kN/m, l1=8 m, l2 = 6m
Mêmes données et questions que pour l’exercice 12.1
E=210 Gpa, I=5/12 10-5 m4
Exercice 12.3
1. Déterminer les actions de liaison
Mêmes données et questions que pour l’exercice 12.1 mais
2. Déterminer la rotation en 2
l’appui simple en 2 est remplacé par un ressort de raideur
3. Tracer les diagrammes de N, T et M k=EI/l3 avec l=1 m.
Exercice 12.4
Résoudre l’exercice 5.4 par la méthode des déplacements.
- 21 -](https://image.slidesharecdn.com/40872913-formulaire-de-rdm-130204112444-phpapp01/85/40872913-formulaire-de-rdm-21-320.jpg)







