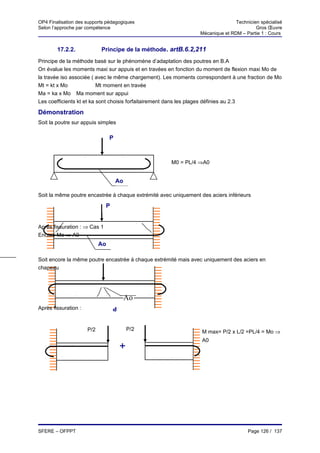
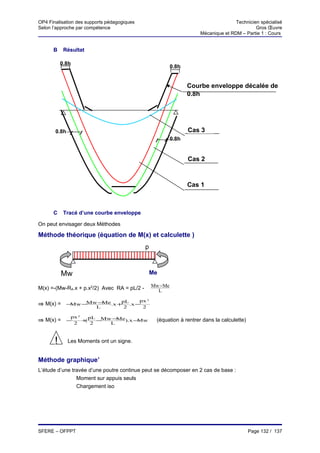
Le document présente les supports pédagogiques pour la formation des techniciens spécialisés en mécanique et résistance des matériaux dans le gros œuvre. Il aborde divers modules couvrant des notions fondamentales telles que la force, les moments, les systèmes équivalents, ainsi que des exercices pratiques. Ces supports sont destinés à améliorer les compétences en ingénierie du bâtiment et des travaux publics.


































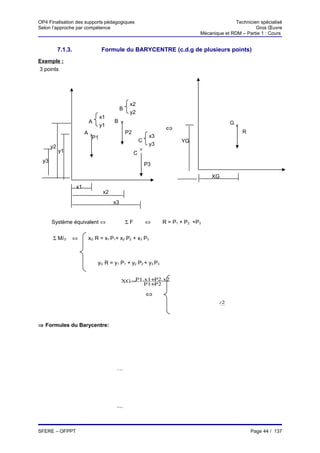


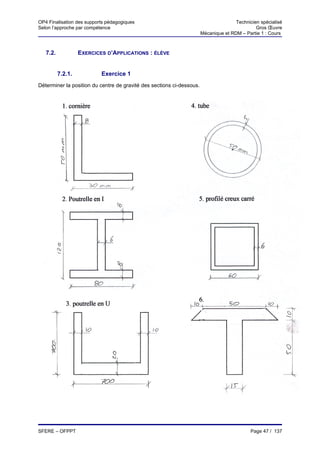
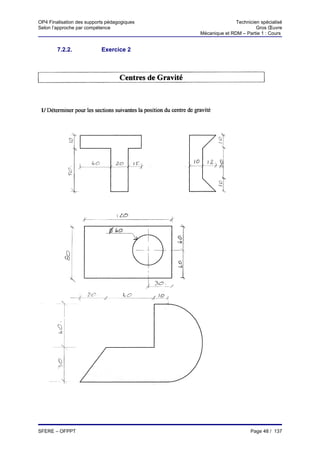
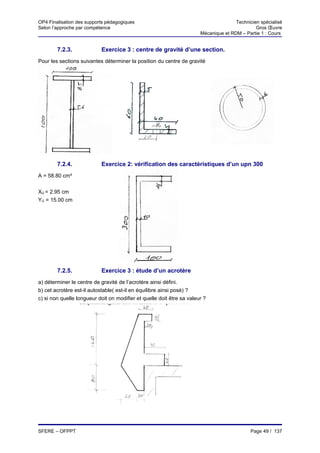






























![OP4 Finalisation des supports pédagogiques Technicien spécialisé
Selon l’approche par compétence Gros Œuvre
Mécanique et RDM – Partie 1 : Cours
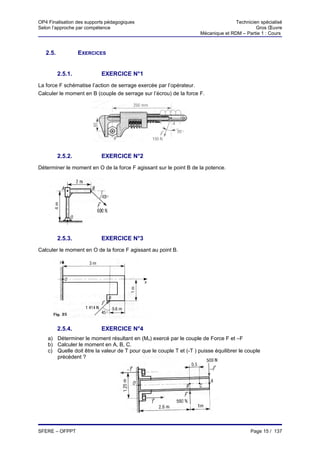
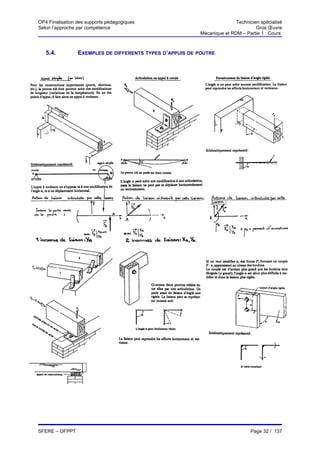
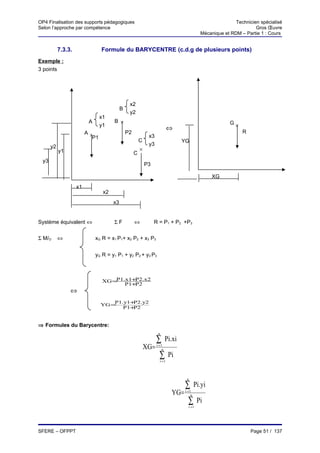
12.1.4. Relations entre V, M et q
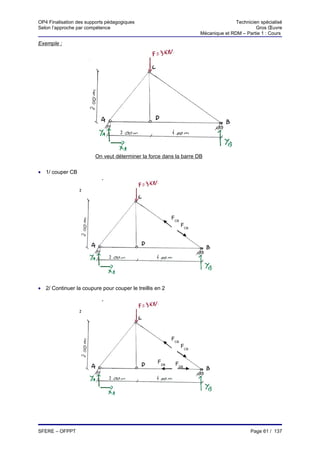
* Soit un tronçon de poutre définie ci-dessous :
q(x)
V
-(M+dM)
M dx -(V+dV)
⇒ Equilibre du tronçon :
∑ proj/oy = 0
V - q(x).dx - V -dV = 0
dV = q(x).dx
dV
⇒ q(x) = −
dx
∑ Mt/oz = 0
dx2
M - V.dx + q(x) - M -dM = 0
2
- V.dx = dM
− dM
V= ⇒ V = 0 ⇒ extremum de M
dx
d2M
+ ⇒ q=
dx 2
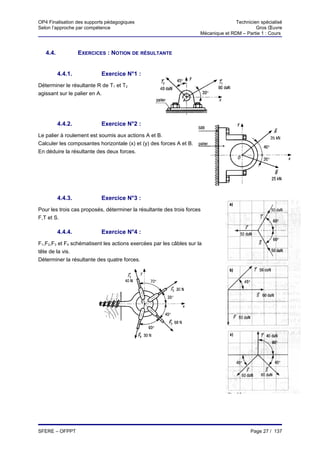
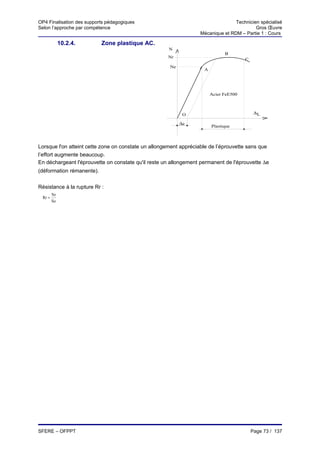
12.1.5. Allure des diagrammes
Charge uniformément Charge triangulaire
Charge concentrée
répartie p(x) = p.x
V(x)
M(x)
Remarque :
x0 x1
m0
m1
x1 x1
dM = -Vdx ⇒ ∫dM = ∫−Vdx
x0 x0
x1
⇒ [M ] x1
x0
=− ∫Vdx ⇒
x
M1−M 0 =−∫ 1V dx
x0
x0
SFERE – OFPPT Page 87 / 137](https://image.slidesharecdn.com/mcaniqueetrdmpartie1-120926134107-phpapp01/85/Mecanique-et-rdm-partie1-87-320.jpg)
![OP4 Finalisation des supports pédagogiques Technicien spécialisé
Selon l’approche par compétence Gros Œuvre
Mécanique et RDM – Partie 1 : Cours
x1
⇒ [ M ] x =− ∫Vdx
1
x
0
⇒
x
M1−M 0 =−∫ 1V dx
x0
x0
⇒ M0 = aire à droite de S de l’effort tranchant. + M1
SFERE – OFPPT Page 88 / 137](https://image.slidesharecdn.com/mcaniqueetrdmpartie1-120926134107-phpapp01/85/Mecanique-et-rdm-partie1-88-320.jpg)