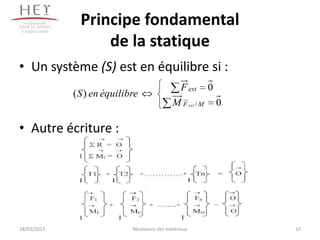
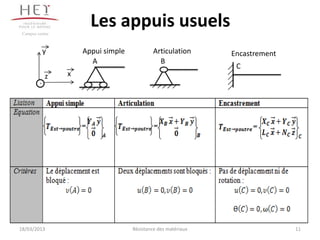
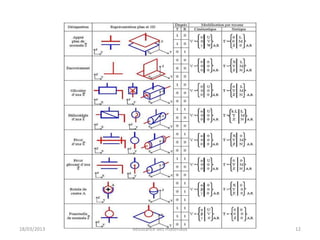
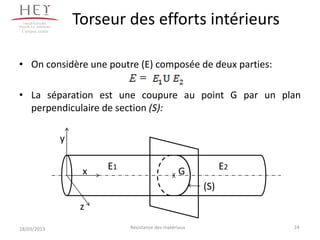
Le document traite de la résistance des matériaux, qui est la mécanique des solides déformables, et aborde des concepts essentiels tels que les caractéristiques des matériaux, la dimension des pièces en fonction des efforts, ainsi que la déformation de celles-ci. Il explore également des principes fondamentaux de la statique, des hypothèses de base de la résistance des matériaux, et des notions telles que le torseur des efforts intérieurs et la contrainte. Des exercices pratiques sur le calcul des réactions d'appui de poutres sont inclus pour illustrer les concepts discutés.

1. Campus centre
Résistance des matériaux
Cours de tronc commun
Mouna SOUISSI
Mouna.souissi@hei.fr
18/03/2013 Résistance des matériaux 1

2. Campus centre
Résistance des matériaux
• La résistance des matériaux est la mécanique
des solides déformables. Elle permet de :
• Caractériser les matériaux ;
• Dimensionner une pièce à partir des efforts qu’elle
supporte ;
• Déterminer la déformation d’une pièce à partir des
efforts qu’elle supporte ;
• Déterminer les efforts maximums que peut supporter
une pièce.
18/03/2013 Résistance des matériaux 2

3. Campus centre
Résistance des matériaux
Sous une charge identique les deux poutres n’offrent pas la même résistance.
Il y a alors d’autres caractéristiques autres que l’aire de la section à connaitre.
18/03/2013 Résistance des matériaux 3

4. Plan
1. Rappels de statique
2. Hypothèses de la Résistance des Matériaux
3. Caractéristiques mécaniques des matériaux
4. Traction – Compression
5. Cisaillement simple
6. Torsion pure
7. Flexion pure
8. Flexion simple
9. Sollicitations composées
18/03/2013 Résistance des matériaux 4

5. Campus centre
Chapitre 1
Rappels de statique

6. Énoncé avec les
Campus centre
forces et les moments
• La force : Un représentant du vecteur force est
caractérisé par 4 éléments :
• la direction : orientation de la force
• le sens : vers où la force agit
• la norme : grandeur de la force, elle est mesurée en (N)
• le point d'application : endroit où la force s'exerce
18/03/2013 Résistance des matériaux 6

7. .
Énoncé avec les
Campus centre
forces et les moments
• Le moment d'une force:
– Le moment d'une force F s'exerçant au point P par rapport
au pivot , est le vecteur:
18/03/2013 Résistance des matériaux 7

8. :
Campus centre
Principe des actions
mutuelles
• Deux ressorts , de masses négligeables D1 et D2, sont en
équilibre . Il existe deux forces de contact qui ont des valeurs
identiques :
•Ces vecteurs forces ont
les mêmes valeurs et ligne
d'action (la droite D1D2)
mais leur sens est opposé. On
note :
18/03/2013 Résistance des matériaux 8

9. Campus centre
Principe fondamental
de la statique
• Si un système de solides est en équilibre, alors la somme des
actions mécaniques extérieures à ce solide ou ce système est nulle.
• Solide ou système de solides : ensemble de 1 à plusieurs solides au
moins assemblés deux à deux
• Équilibre : le solide n’est pas en mouvement par rapport à un
système Galiléen
• Actions mécaniques extérieures : qui dit extérieures, dit intérieures
et dit forcement frontière entre les deux milieux c’est ce que l’on
va appeler la frontière d’isolement.
18/03/2013 Résistance des matériaux 9

10. Campus centre
Principe fondamental
de la statique
• Un système (S) est en équilibre si :
F ext 0
( S ) en équilibre
M F ext / M 0
• Autre écriture :
18/03/2013 Résistance des matériaux 10

11. Campus centre
Les appuis usuels
y Appui simple Articulation Encastrement
A B
C
z x
.
18/03/2013 Résistance des matériaux 11

12. 18/03/2013 Résistance des matériaux 12

13. Campus centre
Structure isostatiques et
hyperstatiques
• Pour une structure plane, les équations sont au nombre de 3.
Soit R le nombre des inconnues des réactions d’appui d’une
structure plane chargée dans son plan.
• Si R =3, les équations de la statique permettent de déterminer
les réactions d’appui structure isostatique extérieurement.
• Si R>3, le nombre des équations d’équilibre est insuffisant
pour permettre le détermination des réactions d’appui. La
structure est hyperstatique d’ordre R-3.
• Si R<3, l’équilibre de la structure ne peut être assuré .la
structure est instable il s’agit d’un mécanisme.
18/03/2013 Résistance des matériaux 13

14. Campus centre
Application
Exercice 1: Calculer les réactions d’appui de la poutre
18/03/2013 Résistance des matériaux 14

15. Campus centre
Application
Exercice 2: Calculer les réactions d’appui de la poutre
18/03/2013 Résistance des matériaux 15

16. Campus centre
Hypothèses de la RDM
• Matériau:
– Homogène
– Isotrope :
– Elastique linéaire :
• Les hypothèses fondamentales de le rdm
– Principe de Saint Venant
– Hypothèse de Bernoulli
– Conditions aux limites
18/03/2013 Résistance des matériaux 16

17. Campus centre
Hypothèses de la RDM
Les solides:
En RDM, les solides étudiés portent le nom de poutres.
Par définition, une poutre est un solide engendré par une surface plane (S) dont le
centre de gravité G décrit une courbe ( (la ligne moyenne), (S) restant
perpendiculaire à ( .
 très long / à ses dimensions
transversales,
 ( rectiligne ou à très faible
courbure,
 section constante (S) ou lentement
variable.
18/03/2013 Résistance des matériaux 17

18. Campus centre
Hypothèses de la RDM
Les matériaux :
Les matériaux utilisés doivent être :
 homogènes : mêmes propriétés mécaniques en tout point,
 isotropes : en un même point, mêmes propriétés mécaniques dans
toutes les directions (non vérifié pour le bois, les matériaux
composites…).
Les déformations:
Les déformations doivent être :
 petites réversibles,
 lentes à chaque instant le corps peut être considéré
comme étant en équilibre statique.
18/03/2013 Résistance des matériaux 18

19. Campus centre
Hypothèses de la RDM
Les déformations:
 Hypothèse de SAINT VENANT
Les résultats obtenus par un calcul de RdM sur une poutre
ne sont valables qu’à une distance suffisamment éloignée de
la région d’application des actions mécaniques extérieures
concentrées et des liaisons
18/03/2013 Résistance des matériaux 19

20. Campus centre
Hypothèses de la RDM
Les déformations:
 Hypothèse de BERNOUILLI
Les sections droites planes et perpendiculaires à la ligne moyenne,
restent planes et perpendiculaires à la ligne moyenne après
déformation.
18/03/2013 Résistance des matériaux 20

21. Campus centre
Hypothèses de la RDM
Les déformations:
Principe de SUPERPOSITION
La déformation (ou la contrainte) en un point M de la poutre due à
plusieurs actions mécaniques extérieures est égale à la somme des
déformations (ou des contraintes) dues à chaque action
mécanique extérieure prise isolément.
Intérêt: ramener un système composé (complexe) à une somme
de systèmes simples.
18/03/2013 Résistance des matériaux 21

22. Campus centre
Hypothèses de la RDM
Conditions aux limites :
Efforts extérieurs : Les efforts extérieurs qui s’appliquent au modèle poutre
sont principalement de deux types.
•concentrées,
•réparties de façon continue.
Liaisons : Les liaisons que l’on rencontre sont les liaisons classiques
y Appui simple Articulation Encastrement
A B
C
z x
.
18/03/2013 Résistance des matériaux 22

23. Campus centre Torseur des efforts intérieurs
notions contraintes
• On aborde deux notions fondamentales pour
la RdM :
• le torseur des efforts intérieurs ;
• la notion de contrainte.
18/03/2013 Résistance des matériaux 23

24. Campus centre
Torseur des efforts intérieurs
• On considère une poutre (E) composée de deux parties:
• La séparation est une coupure au point G par un plan
perpendiculaire de section (S):
y
x E1 G E2
(S)
z
18/03/2013 Résistance des matériaux 24

25. Campus centre
Torseur des efforts intérieurs
1)Expression du torseur des efforts intérieurs
Equilibre de l’aval (E2):
18/03/2013 Résistance des matériaux 25

26. Campus centre
Torseur des efforts intérieurs
1)Expression du torseur des efforts intérieurs
Equilibre de l’amant (E1):
18/03/2013 Résistance des matériaux 26

27. Campus centre
Torseur des efforts intérieurs
1)Expression du torseur des efforts intérieurs
Bilan et règle de calcul et synthèse:
18/03/2013 Résistance des matériaux 27

28. Campus centre
Torseur des efforts intérieurs
2) Composantes du torseur de section:
Dans le repère local le torseur des efforts intérieurs est exprimé par :
18/03/2013 Résistance des matériaux 28

29. Campus centre
Torseur des efforts intérieurs
3) Les sollicitations élémentaires :
Nature des sollicitations Forces de cohésion
Traction
ou N
Compression
Cisaillement simple T
Torsion simple Mt
Flexion pure Mf
Flexion simple T+Mf
Flexion composée N+T+Mf
18/03/2013 Résistance des matériaux

30. Campus centre
Notion de contraintes
• Le torseur de cohésion ne représente qu’une vision
globale sur la section droite de toutes les actions
mécaniques qui s’appliquent localement en chaque
point de la surface.
• Ces actions mécaniques locales sont réparties sur
toute la surface suivant une loi à priori inconnue. Pour
les représenter, considérons un point M de la surface S.
• Autour de ce point M on considère un petit élément
de surface dS de normale .
18/03/2013 Résistance des matériaux 30

31. Campus centre
Notion de contraintes
• En RdM les efforts intérieurs exercés sur dS sont une densité
surfacique d’efforts ou densité de force par unité de surface.
Cette densité surfacique d’effort est caractérisée par le
vecteur contrainte:
Les actions mécaniques qui s’exercent sur la surface dS sont
donc :
18/03/2013 Résistance des matériaux 31