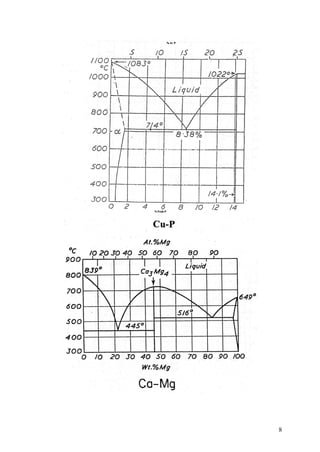
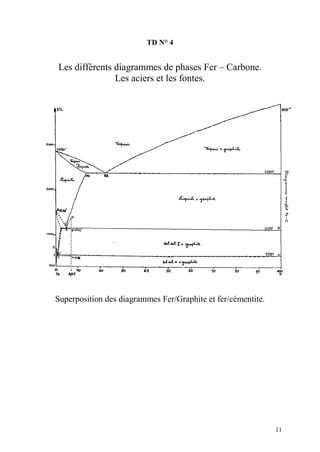
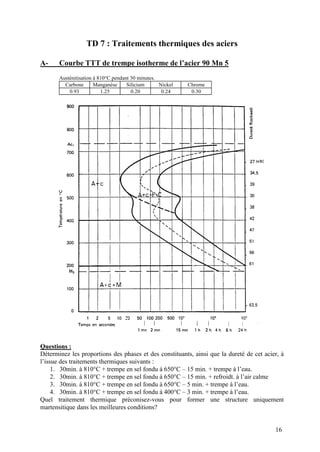
Le document aborde divers travaux dirigés en science des matériaux concernant des courbes de traction d'acier inoxydable, les contraintes thermiques de dilatation, ainsi que des études sur des diagrammes de phases du cuivre-antimoine et du fer-carbone. Il contient des questions et des calculs relatifs aux propriétés mécaniques et thermiques de différents matériaux, ainsi qu'à la structure cristallographique du fer. Des traitements thermiques et des désignations normalisées des alliages ferreux sont également discutés.

1. Travaux dirigés de Science des Matériaux
Année 2013 - 2014
M. Souissi
J.Y. Dauphin
1

2. 2

3. TD N° 1 Etude d’une courbe de traction.
Courbe de traction d’un acier inoxydable
Conditions de mesure : mesure de l’allongement par déplacement de traverse - Vitesse de déformation constante = 1.5 10-2 sec.-1.
Longueur initiale L0 = 50 mm - Diamètre initial D0 = 10 mm.
Force maximale Fm
47127 N
50000
45000
20000
40000
Newtons
18000
35000
Force ultime Fu
40840 N
Force en Newton
16000
30000
14000
12000
25000
10000
20000
8000
6000
15000
4000
10000
2000
mm
5000
0
0
0,1
0,2
0,3
0,4
0
0
5
10
15
Allongement en millimètres
19 20
22
25
3

4. TD 1 : Questions relatives à la courbe de traction de l’acier inoxydable
Déterminer :
1) Les caractéristiques de l’élasticité :
a. La limite d’élasticité
b. Le module d’élasticité apparent
2) La résistance maximale en traction
3) Les caractéristiques de déformabilité
a. L’allongement à la rupture
b. Le coefficient de striction (avec Du=6,82 mm)
4) La contrainte vraie à la limite d’élasticité
5) La contrainte vraie à la force maximale
6) La contrainte vraie à la rupture
7) Les paramètres du modèle de déformation de Lüdwik :
Avec V : la contrainte vraie
k : une constante du matériau
n : le coefficient d’écrouissage
 : l’allongement rationnel
et à la charge maximale n=
 v  k n
4

5. TD N° 2
Contraintes thermiques de dilatation
Un échantillon du matériau testé, de longueur L0 à la température initiale T0, est bridé dans un
support massif, supposé indéformable et non dilatable.
L0
On effectue un cycle thermique d’amplitude T avec retour à T0.
Les différentes étapes du cycle peuvent se décomposer fictivement ainsi :
T0, longueur L0
L0
T1 = T0 + , allongement à L1 = L0 + L
Compression  pour ramener à L2 = L0
Retour à T0, L3 = ?
1-/ Calculez la contrainte thermique th qui se développe lorsque le matériau atteint T 1, dans
le cas d’un =100K.
L 1
On rappelle que le coefficient de dilatation linéaire s’écrit :  
, en K-1.
L0 T
2-/ Application à trois matériaux différents :
SiC (céramique)
Ni (métal )
PE (polymère)
E en GPa
480
214
0.9
Re en MPa
10000
200
20
Rm en MPa
10000
200
25
 en K-1
4.7 10-6
13.3 10-6
100 10-6
3-/ Décrivez le comportement mécanique de chacun de ces matériaux lors du cycle.
5

6. TD N° 3 : Description de quelques diagrammes variés
.
6

7. 7

8. 8

9. TD N° 3 : Etude du diagramme d’équilibre de phases du système Cuivre - Antimoine
9

10. TD N°3
Questions concernant le diagramme Cu/Sb
1)
2)
3)
4)
Identifier sur le diagramme les domaines monophasés
Identifier les domaines biphasés en spécifiant les phases en équilibre
Tracer le liquidus et le solidus
Localiser et décrire les transformations s’opérant à température constante
a. Les eutectiques (2)
b. Le péritectique
c. L’eutectoïde
d. Le peritectoïde
e. Le monotectique
f. Y a-t-il d’autres transformations s’effectuant à température constante ?
5) Etude du refroidissement :
a. De la composition à 76,8% Sb
b. De la composition à 47%Sb
10

11. TD N° 4
Les différents diagrammes de phases Fer – Carbone.
Les aciers et les fontes.
Superposition des diagrammes Fer/Graphite et fer/cémentite.
11

12. TD N°4 : Les diagrammes Fer/graphite (en traits pleins) et Fer/Cémentite (en pointillés), du côté riche en fer.
Etudier le
refroidissement des
compositions :
1) 0,85%C
2) 0.30%C
3) 4,47%C
12

13. Diagramme binaire fer/cémentite limité à la zone des aciers.
13

14. N° 5
Etude du système cristallographique du fer
Le fer subit une transformation allotropique à 912°C.
La phase stable à basse température est la ferrite, de structure cubique centrée.
Le paramètre de maille de la ferrite, à 911°C, est de 0.2903 nm.
La structure stable au-delà de cette température est la phase austénite, cubique à face centrées.
A 913°C, le paramètre de l’austénite est de 0.3646 nm.
1)
2)
3)
4)
5)
6)
7)
6)
Calculer la masse volumique du fer à 911°C et à 913°C
Calculer le volume spécifique à 911°C et à 913°C
Calculer la variation de volume et de longueur pour 1g de fer entre 911 et 913°C.
Calculer le diamètre des atomes de fer à 911°C et à 913°C.
Calculer la compacité du fer à ces deux températures
Dénombrer les sites d’insertion.
Calculez le diamètre maximal des atomes qui peuvent s’y loger.
Quelle conclusion peut-on en tirer sur la solubilité du carbone dans le fer ?
Données : MFe=0.05585 kg/mol - Mc = 0.012 kg/mol
c
c
b
a
b
a
Maille de la ferrite (atomes disjoints à gauche et sphères atomiques au contact à droite)
c
c
a
a
b
b
Maille de l’austénite (atomes disjoints à gauche et sphères atomiques au contact à droite)
14

15. TD 6
Désignation normalisée des alliages ferreux.
a-1 Aciers usuels.
La désignation commence par une lettre correspondant à leur emploi, + valeur Re en Mpa.
Ces aciers, dont on ignore la composition, sont impropres à tout traitement thermique.
a-2 Aciers spéciaux non alliés.
Destinés avant tout aux traitements thermiques de pièces petites et moyennes.
La désignation commence par la lettre C, suivie du % de Carbone multiplié par 100.
Suivent parfois des indications complémentaires
exemple
:
C 35 E
a-3 Aciers faiblement alliés pour haute résistance.
Aucun élément d’addition ne dépasse 5%.
Leur nom indique les pourcentages massiques des éléments d’alliage, par ordre
décroissant, multipliés par 4, 10 ou 100.
a-4Aciers fortement alliés.
Destinés à des emplois particuliers (aciers inoxydables, travail à chaud, etc..).
Un élément, au moins, dépasse 5 % en masse.
X, suivi des teneurs des éléments – Plus de coefficient multiplicateur.
Exemple : acier inoxydable X6 CrNiTi 18-11
Pour toutes les classes, s’il s’agit d’un acier moulé, la désignation est précédée de G.
15

16. TD 7 : Traitements thermiques des aciers
A-
Courbe TTT de trempe isotherme de l’acier 90 Mn 5
Austénitisation à 810°C pendant 30 minutes.
Carbone
Manganèse
Silicium
Nickel
0.93
1.25
0.20
0.24
Chrome
0.30
Questions :
Déterminez les proportions des phases et des constituants, ainsi que la dureté de cet acier, à
l’issue des traitements thermiques suivants :
1. 30min. à 810°C + trempe en sel fondu à 650°C – 15 min. + trempe à l’eau.
2. 30min. à 810°C + trempe en sel fondu à 650°C – 15 min. + refroidt. à l’air calme
3. 30min. à 810°C + trempe en sel fondu à 650°C – 5 min. + trempe à l’eau.
4. 30min. à 810°C + trempe en sel fondu à 400°C – 3 min. + trempe à l’eau.
Quel traitement thermique préconisez-vous pour former une structure uniquement
martensitique dans les meilleures conditions?
16

17. B/
Courbe TTT de refroidissement continu de l’acier 50 Cr Mo 4
Austénitisation à 850°C pendant 30 minutes
Carbone
0.52
Hrc
Diam Huile
t700/300
Manganèse
0.60
62
5
12
61
10
23
Silicium
0.40
60
20
38
54
40
88
Nickel
1.00
45
100
190
37
160
417
Chrome
0.17
35
250
750
26
300
900
Questions :
1. Déterminez la vitesse critique de recuit et la vitesse critique de trempe.
2. Mf à partir de Ms, M50 et M90.
3. Les proportions des constituants pour le chemin de refroidissement aboutissant à une
dureté de 37HRc.
4. Tracez la courbe de trempabilité Jominy de cet acier.
5. Quelle est sa dureté critique de trempe?
17

18. 18