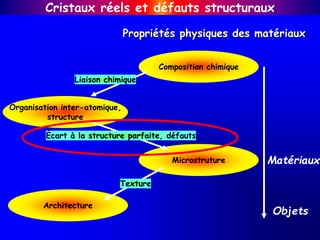
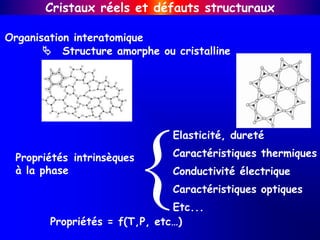
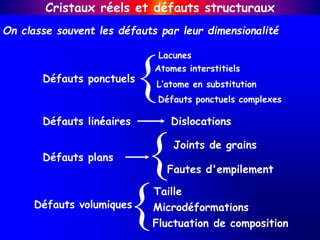
Le document traite des cristaux réels et des défauts structuraux, en expliquant comment les défauts, comme les lacunes et les dislocations, influencent les propriétés physiques des matériaux tels que l'élasticité et la conductivité. Il discute de la classification des défauts selon leur dimensionalité et de l'impact des impuretés et des alliages sur la structure cristalline. Les principes de déformation plastique et les effets des défauts sur les propriétés optiques et électriques des matériaux sont également abordés.


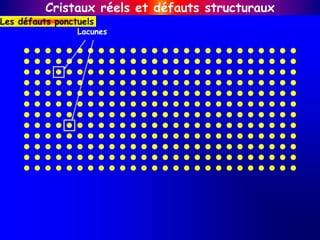
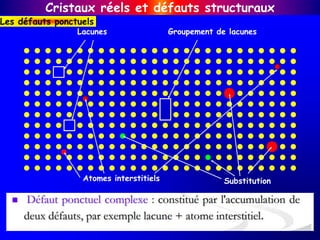

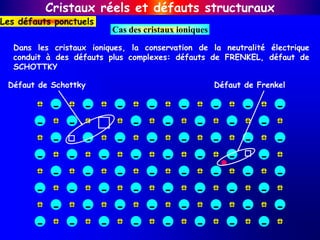









![Cristaux réels et défauts structuraux
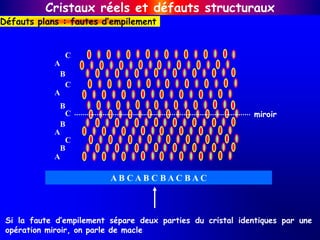
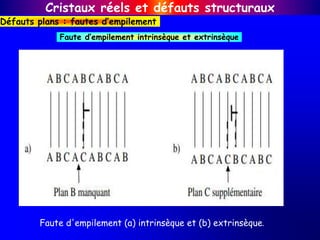
Défauts plans : fautes d’empilement
A
B
C
A
B
C
A
B
C
A
B
C
[111]
[112]
(-110)
[001]
[110]](https://image.slidesharecdn.com/ch-220508162244-ff3339af/85/Ch-3-ppt-19-320.jpg)






![III- Déformation plastique
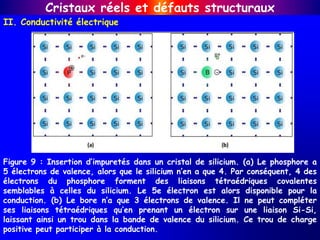
Cristaux réels et défauts structuraux
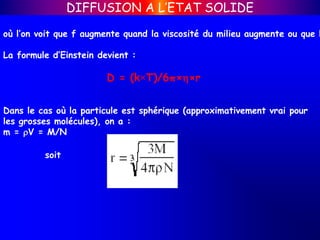
Nous considérons un barreau de matière soumis à une contrainte de
traction uniaxiale. On exerce dans ce cas une force F parallèlement à l’axe
de la section S [Figure 10 a]. La valeur de la contrainte se calcule comme le
rapport de la force sur la surface :
Sous l’action de la force F , le solide se déforme suivant l’axe de la
contrainte. On définit mathématiquement la déformation correspondante
comme , l’allongement relatif dans la direction de la contrainte.
Figure 10 : (a) Barre cylindrique soumise à une contrainte de traction
uniaxiale. (b) Relation schématique entre contrainte et déformation dans un
matériau solide. OL est le domaine élastique, et LR est le domaine plastique](https://image.slidesharecdn.com/ch-220508162244-ff3339af/85/Ch-3-ppt-29-320.jpg)
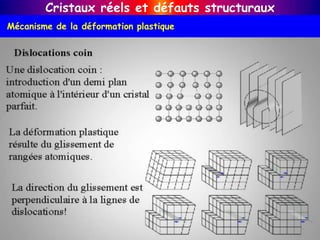
![Mécanisme de la déformation plastique
Dans le domaine de déformation élastique, les faibles contraintes
appliquées au solide déplacent légèrement les atomes par rapport à leurs
positions d’équilibre, vers lesquelles ils reviennent lorsque la sollicitation
extérieure diminue. Au contraire, les déformations obtenues dans le
domaine plastique persistent après relâchement de la contrainte
extérieure, posant la question de la nature des changements structuraux
subis par l’échantillon.
L’observation par microscopie optique de monocristaux métalliques soumis à
des contraintes de traction élevées révèle l’apparition de traces de
glissement lors de la déformation plastique [Figure 11 a]. Ces traces ont été
très tôt interprétées comme la conséquence du glissement de plans
cristallins les uns par rapport aux autres [Figure 11b].
Cristaux réels et défauts structuraux](https://image.slidesharecdn.com/ch-220508162244-ff3339af/85/Ch-3-ppt-30-320.jpg)