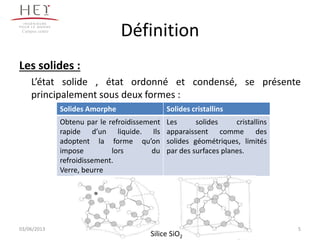
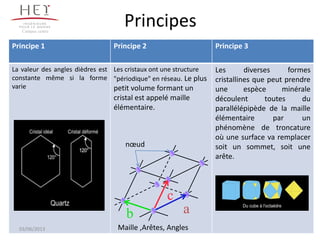
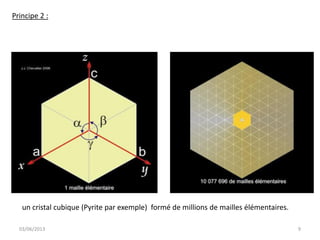
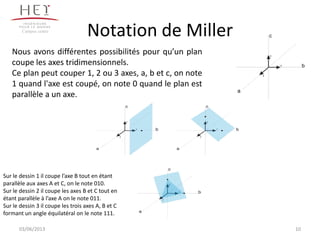
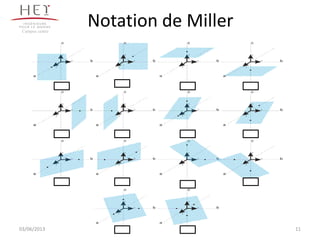
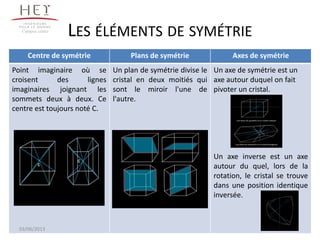
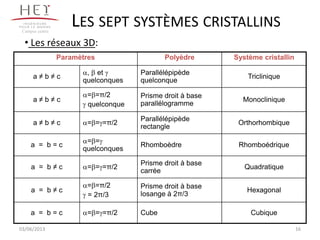
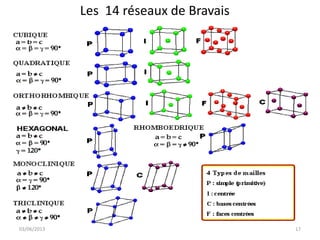
La cristallographie est une science qui étudie la formation et les caractéristiques géométriques des cristaux, distinguant entre solides cristallins et amorphes. Le document couvre les principes des structures cristallines, la notation de Miller, les systèmes et réseaux cristallins, ainsi que les types de défauts présents dans les cristaux. Les caractéristiques telles que la masse volumique, la coordinance et la compacité sont également abordées, illustrant leur impact sur les propriétés matérielles.

1. Science des Matériaux
1
Campus centre
Les solides cristallisés et les défauts cristallins
Mouna SOUISSI
mouna.souissi@hei.fr
03/06/2013

2. Plan
• Définition
• Principes
• Notation de Miller
• Les éléments de symétrie
• Systèmes et réseaux
• Caractéristiques à définir
• Sites cristallographiques
• Les défauts cristallins
• Applications
2
Campus centre
03/06/2013

3. Définition
• La cristallographie :
Est La science qui étudie la formation, la forme et les
caractéristiques géométriques des cristaux.
• Une matière cristalline est un matériau à l'état solide dont
les composants chimiques, atomes et molécules sont
disposés selon un schéma ordonné tridimensionnel.
• Lorsqu'un solide n'est pas cristallin on dit qu'il est amorphe
(sans forme).
Campus centre
303/06/2013

4. Définition
4
Campus centre
03/06/2013

5. Définition
Les solides :
L’état solide , état ordonné et condensé, se présente
principalement sous deux formes :
Campus centre
5
Solides Amorphe Solides cristallins
Obtenu par le refroidissement
rapide d’un liquide. Ils
adoptent la forme qu’on
impose lors du
refroidissement.
Verre, beurre
Les solides cristallins
apparaissent comme des
solides géométriques, limités
par des surfaces planes.
Silice SiO2
03/06/2013

6. Définition
• Un cristal est caractérisé par la répétition
tridimensionnelle d'un "motif" (atomes,
molécules, …) sur une très grande distance.
• Le réseau cristallin est un assemblage de
lignes fictives qui rend compte de la répétition
des nœuds et matérialise les vecteurs de
translation.
6
Campus centre
03/06/2013

7. Définition
7
Campus centre
03/06/2013

8. Principes
8
Campus centre
Principe 1 Principe 2 Principe 3
La valeur des angles dièdres est
constante même si la forme
varie
Les cristaux ont une structure
"périodique" en réseau. Le plus
petit volume formant un
cristal est appelé maille
élémentaire.
Les diverses formes
cristallines que peut prendre
une espèce minérale
découlent toutes du
parallélépipède de la maille
élémentaire par un
phénomène de troncature
où une surface va remplacer
soit un sommet, soit une
arête.
ab
c
nœud
Maille ,Arêtes, Angles03/06/2013

9. 9
un cristal cubique (Pyrite par exemple) formé de millions de mailles élémentaires.
Principe 2 :
03/06/2013

10. Notation de Miller
10
Campus centre
Nous avons différentes possibilités pour qu’un plan
coupe les axes tridimensionnels.
Ce plan peut couper 1, 2 ou 3 axes, a, b et c, on note
1 quand l'axe est coupé, on note 0 quand le plan est
parallèle a un axe.
Sur le dessin 1 il coupe l’axe B tout en étant
parallèle aux axes A et C, on le note 010.
Sur le dessin 2 il coupe les axes B et C tout en
étant parallèle à l’axe A on le note 011.
Sur le dessin 3 il coupe les trois axes A, B et C
formant un angle équilatéral on le note 111.
03/06/2013

11. Notation de Miller
11
Campus centre
03/06/2013

12. LES ÉLÉMENTS DE SYMÉTRIE
• Les principaux éléments de symétrie sont :
– Le centre de symétrie
– Les plans de symétrie
– Les axes de symétrie
12
Campus centre
03/06/2013

13. LES ÉLÉMENTS DE SYMÉTRIE
13
Campus centre
Centre de symétrie Plans de symétrie Axes de symétrie
Point imaginaire où se
croisent des lignes
imaginaires joignant les
sommets deux à deux. Ce
centre est toujours noté C.
Un plan de symétrie divise le
cristal en deux moitiés qui
sont le miroir l'une de
l'autre.
Un axe de symétrie est un
axe autour duquel on fait
pivoter un cristal.
Un axe inverse est un axe
autour du quel, lors de la
rotation, le cristal se trouve
dans une position identique
inversée.
03/06/2013

14. Systèmes et réseaux
• Il existe 7 systèmes cristallins simples.
Les systèmes "simples" ne contiennent qu'un motif par maille =
maille dite "élémentaire«
• Il existe d’autres systèmes qui contiennent plusieurs motifs
=mailles dites "multiples".
 systèmes "centrés" (avec un atome au centre de la maille)
 systèmes faces centrées (avec un atome au centre de chaque face)
 systèmes bases centrées (avec un atome au centre de 2 seulement
des faces).
• L’ensemble de ces systèmes forment les 14 réseaux
de Bravais .
14
Campus centre
03/06/2013

15. LES SEPT SYSTÈMES CRISTALLINS
15
Campus centre
03/06/2013

16. Campus centre
16
Paramètres Polyèdre Système cristallin
a ≠ b ≠ c
,  et 
quelconques
Parallélépipède
quelconque
Triclinique
a ≠ b ≠ c
==π/2
 quelconque
Prisme droit à base
parallélogramme
Monoclinique
a ≠ b ≠ c ===π/2
Parallélépipède
rectangle
Orthorhombique
a = b = c
==
quelconques
Rhomboèdre Rhomboédrique
a = b ≠ c ===π/2
Prisme droit à base
carrée
Quadratique
a = b ≠ c
==π/2
 = 2π/3
Prisme droit à base
losange à 2π/3
Hexagonal
a = b = c ===π/2 Cube Cubique
• Les réseaux 3D:
03/06/2013
LES SEPT SYSTÈMES CRISTALLINS

17. 17
Les 14 réseaux de Bravais
03/06/2013

18. Campus centre
18
Les types de mailles
03/06/2013

19. • Z : Le nombre de motifs par maille.
• Si un motif/nœud se partage entre n maille il ne compte que 1/n pour
chacune d’elles.
• Exemple:
• Un élément extérieur à la maille ne lui appartient pas compte :
• Un élément placé au sommet d’une maille appartient à 8 maille
• Un élément placé sur une arête d’une maille appartient à 4 maille
• Un élément placé sur une face d’une maille appartient à 2 maille
• Un élément placé à l’intérieur d’une maille appartient à elle seule….
Campus centre
19
Caractéristiques à définir
Nombre de motifs
03/06/2013

20. Caractéristiques à définir
Nombre de motifs
• Déterminer Z pour :
– Une maille P
– Une maille I
– Une maille C
– Une maille F
20
Campus centre
03/06/2013

21. Caractéristiques à définir
Masse volumique
• Le nombre de motif + la masse molaire du motif permettent
de déterminer la masse volumique du solide cristallin.
21
Campus centre
Par définition la masse volumique:
Pour une seule maille on a :
masse de la maille = z . masse du motif = z . Masse molaire du motif /N
d’où:
z =nombre de motifs par maille
Mmotif = masse molaire du motif
N = nombre d’Avogadro
vmaille = volume de la maille
03/06/2013

22. Caractéristiques à définir
Coordinence
• La coordinance de l’atome Ai est le nombre x
de ses atomes plus proches voisins V.
• On la note A/V=x ou C(a/V)=x.
• Exemple:
22
Campus centre
03/06/2013

23. Caractéristiques à définir
Compacité
• La compacité C est un nombre sans dimension qui mesure le
taux d’occupation réel de l’espace par les atomes ou les ions
assimilés à des sphères dures.
• Elle est toujours comprise entre 0 et 1.
• Souvent on l’exprime en pourcentage.
• Exemple:
23
Campus centre
03/06/2013

24. Sites cristallographiques
• Les sites cristallographiques ou sites interstitiels sont les interstices
ou lacune de matière dans une maille.
• Il existe 3 sortes de sites cristallographiques:
– Les sites cubiques
– Les sites octaédriques
– Les sites tétraédriques
• Les atomes les plus petits, H, B, C et N, peuvent s’intégrer par
insertion dans les « trous » des réseaux cristallins grâce à leur petite
taille. Ces trous sont les sites interstitiels. Chaque structure
cristalline possède des sites plus ou moins accueillants pour ces
atomes dont l’influence sur les propriétés est très grande.
24
Campus centre
03/06/2013

25. Les défauts cristallins
• Le cristal parfait n’existe pas. Les atomes ne
sont pas placés systématiquement à l’endroit
prévu que cela soit dans le réseau cristallin de
base ou dans les sites d’insertion ou de
substitution.
• Il y a trois type de défauts:
– les défauts ponctuels
– les défauts linéaires
– les défauts surfaciques
25
Campus centre
03/06/2013

26. Application
• Structure cubique à faces centrée CFC (F)
• Structure hexagonale compact: h.c (H)
• Structure cubique centrée
– Paramètres de maille et relation entre a et R
– Nombre de motif par maille
– Coordinence
– Compacité
– Sites interstitiels
03/06/2013 26