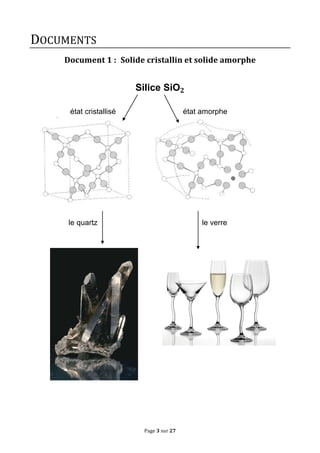
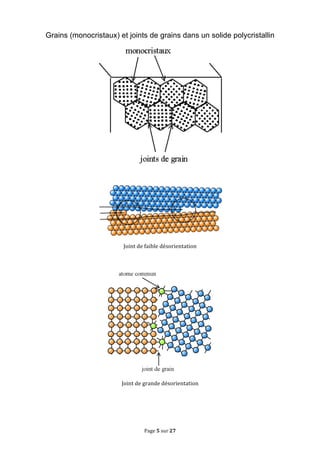
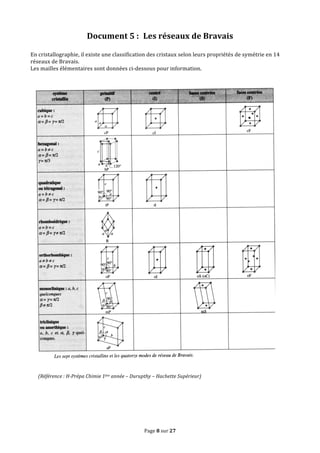
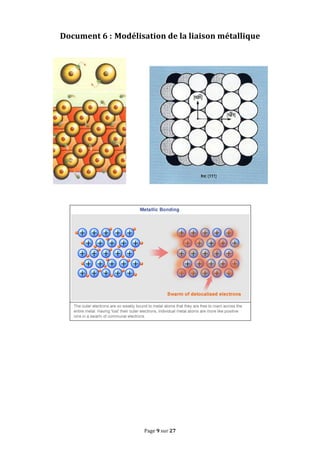
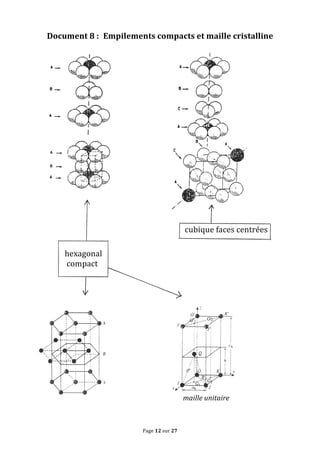
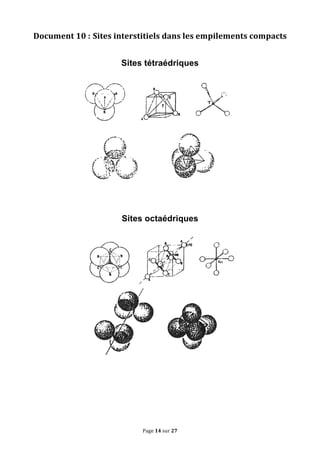
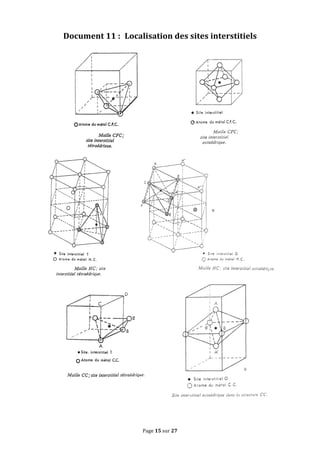
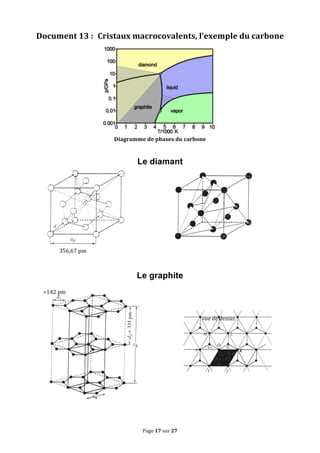
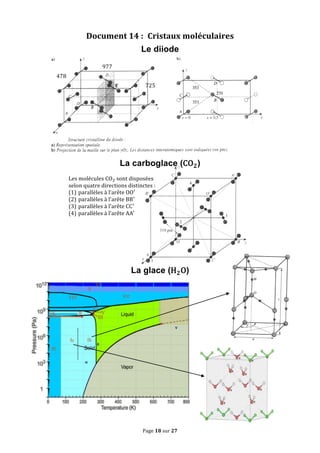
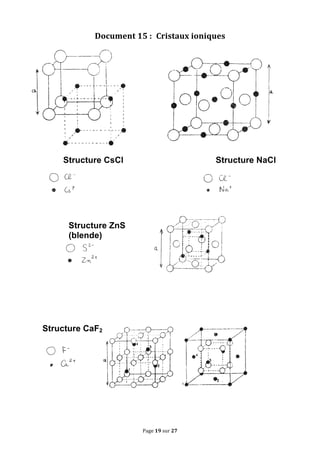
Le document traite des concepts fondamentaux de la cristallographie en abordant les structures des solides cristallins, amorphes, métaux, cristaux covalents et ioniques. Il couvre des notions telles que les mailles cristallines, les interstices dans les empilements, ainsi que les propriétés des matériaux en relation avec leur structure atomique. Des exercices sur des métaux comme le magnésium et le niobium illustrent les concepts théoriques abordés dans le chapitre.