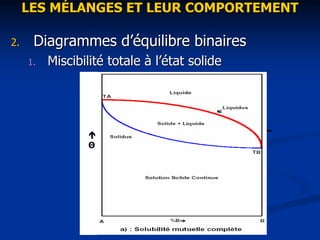
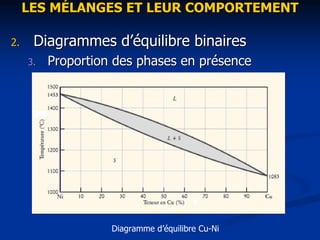
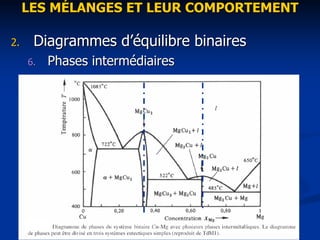
Le document traite des mélanges et de leur comportement, en introduisant des concepts tels que la définition des phases, la règle de phase de Gibbs et l'analyse des diagrammes d'équilibre binaires. Les diagrammes illustrent les conditions d'équilibre des phases, la miscibilité des composants et différentes transformations des phases, comme les transformations eutectiques et péritectiques. Enfin, il aborde les considérations générales concernant les diagrammes d'équilibre et les limites des domaines d'existence des mélanges.