Téléchargé 26 fois
Téléchargé parMouna Souissi
Chapitre 6
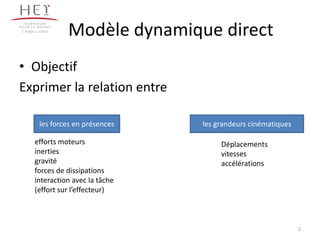
Le document traite des modèles dynamiques direct et inverse pour exprimer la relation entre diverses forces et les grandeurs cinématiques d'un système. Il examine les équations différentielles non linéaires et l'utilisation des formalismes d'Euler-Newton et de Lagrange pour évaluer les caractéristiques mécaniques des actuateurs. L'approche de Lagrange est décrite comme plus systématique mais plus complexe numériquement.
Chapitre 6
- 1. Campus centre Chapitre 6 MounaSouissi Mouna.souissi@hei.fr 1
- 2. Campus centre Modèle dynamiquedirect • Objectif Exprimer la relation entre les forces en présences efforts moteurs inerties gravité forces de dissipations interaction avec la tâche (effort sur l’effecteur) les grandeurs cinématiques Déplacements vitesses accélérations 2
- 3. Campus centre Modèle dynamiquedirect • Données: efforts appliqués C(t) + état initial • Résultats: • variables articulaires Θ(t) • trajectoire dans l’espace de travail X(t) On obtient un système non-linéaire d’équations différentielles du second ordre à intégrer dans le temps 3
- 4. Campus centre Modèle dynamiqueinverse • Données: trajectoire X(t) • Résultats: efforts nécessaires C(t) pour atteindre ou maintenir une configuration Objectif : évaluation des caractéristiques mécaniques des actuateurs et des organes de transmissions et prédire le comportement dynamique du système. dimensionnement des moteurs et actuateurs 4
- 5. Campus centre Modèle dynamiqueinverse • FORMALISMES POSSIBLES EULER-NEWTON • schéma rendu libre des composants isolés • équilibre dynamique des membres • bien adapté à une procédure récursive conduisant à un nombre minimum d’opérations arithmétiques LAGRANGE • basé sur les équations de Lagrange du système • basé sur l ’évaluation des énergies cinétique et potentielle due à la gravité, et le travail virtuel des forces et couples extérieurs • approche plus systématique • mais procédure récursive plus compliquée et donc de coût numérique plus élevé 5
- 6. Campus centre Formalisme delagrange • Considérons un robot idéal sans frottement, sans élasticité et ne subissant ou exerçant aucun effort extérieur. • Le formalisme de Lagrange décrit les équations du mouvements en terme de travail et d’énergie du système : • • • L : lagrangien du système égale à E-U E : énergie cinétique totale du système U : énergie potentiel totale du système 6
- 7. Campus centre Formalisme delagrange 7
- 8. Campus centre Formalisme delagrange Expression du modèle du robot : 8