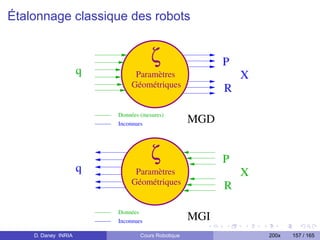
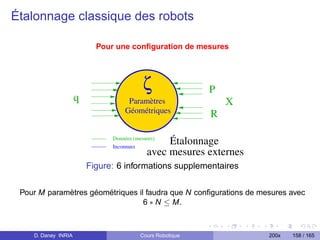
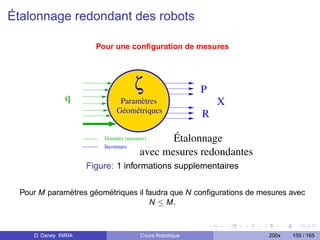
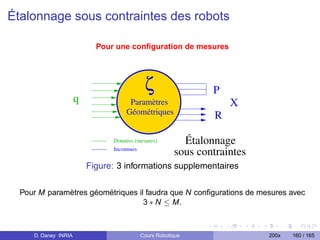
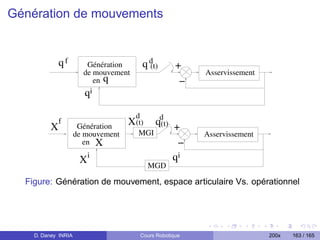
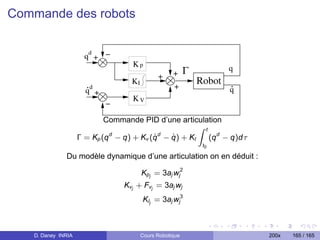
Le document présente un cours sur la robotique, décrivant son histoire et ses applications à travers les âges, des mythes antiquités aux avancées contemporaines. Il traite des notions techniques fondamentales comme les transformations rigides, les manipulateurs, et les modèles dynamiques des robots. En outre, il clarifie la définition d'un robot et explore sa progression historique, en soulignant des milestones clés et des contributions significatives dans le domaine.


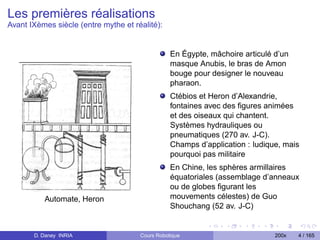






































































![Les articulations des robots
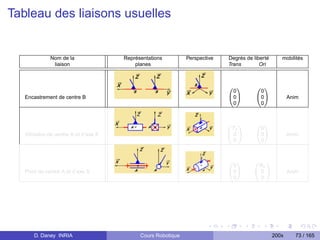
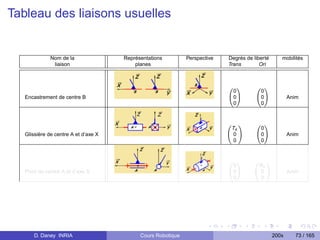
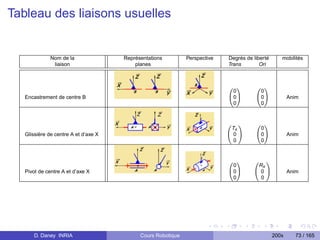
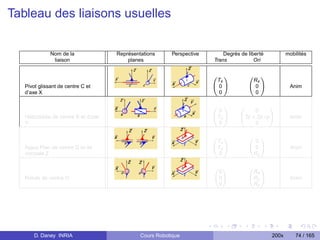
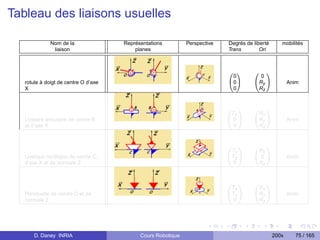
Articulation prismatique, noté P Articulation rotoïde, noté R
1 ddl en translation Tz . 1 ddl en rotation Rz .
Valeur articulaire q = longueur [m]. Valeur articulaire q = angle [rad], [◦ ].
D. Daney INRIA Cours Robotique 200x 77 / 165](https://image.slidesharecdn.com/robotique-120802172903-phpapp01/85/Robotique-100-320.jpg)
![Les articulations des robots
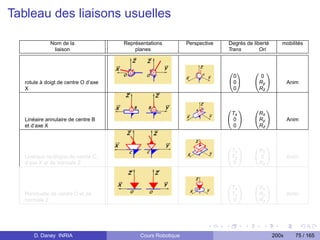
Articulation prismatique, noté P Articulation rotoïde, noté R
1 ddl en translation Tz . 1 ddl en rotation Rz .
Valeur articulaire q = longueur [m]. Valeur articulaire q = angle [rad], [◦ ].
D. Daney INRIA Cours Robotique 200x 77 / 165](https://image.slidesharecdn.com/robotique-120802172903-phpapp01/85/Robotique-101-320.jpg)




![Vocabulaire
Coordonnées généralisé X = [P, R]
(position P / orientation R)
Coordonnées articulaire q
(consignes données aux moteurs : soit rotation autour d’un axe soit
translation suivant un axe)
Paramètres géométriques ζ
qui définissent de façon statique les dimension du robot
D. Daney INRIA Cours Robotique 200x 83 / 165](https://image.slidesharecdn.com/robotique-120802172903-phpapp01/85/Robotique-108-320.jpg)

























![Calculer le MDG
Déterminer:
X=( 0R 0 P )
0 1
X = FMGD (q1 , q2 , . . . , qi , ζ)
Repère mobile
q4 La transformation homogène entre le
q3 repère Ω0 et le repère mobile Ωn est
q2 obtenue telle que :
q1
HCK = H0 .H1 . . . Hn
Repère de base
Il faut projeter HCK sur X = [Tx , Ty , Tz , Rx , Ry , Rz ]
D. Daney INRIA Cours Robotique 200x 111 / 165](https://image.slidesharecdn.com/robotique-120802172903-phpapp01/85/Robotique-142-320.jpg)
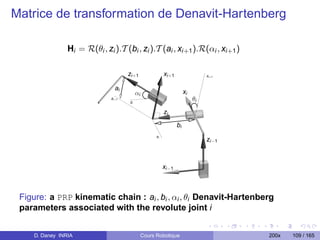
![De la matrice DH vers 6 parameters
Tx , Ty , Tz , Rx , Ry , RZ
Nous souhaitons obtenir X = [Tx , Ty , Tz , Rx , Ry , Rz ] en fonction de des
élément de la matrice HCK .
Pour la position ...
Tx HCK 1,4
Ty = HCK 2,4
Tz HCK 3,4
D. Daney INRIA Cours Robotique 200x 112 / 165](https://image.slidesharecdn.com/robotique-120802172903-phpapp01/85/Robotique-143-320.jpg)
![De la matrice DH vers 6 parameters
Tx , Ty , Tz , Rx , Ry , RZ
Nous souhaitons obtenir X = [Tx , Ty , Tz , Rx , Ry , Rz ] en fonction de des
élément de la matrice HCK .
Pour l’orientation ...
Sachant que :
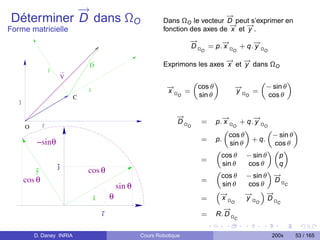
cos θ cos ψ − cos θ sin ψ sin θ
R = sin φ sin θ cos ψ + cos φ sin ψ cos φ cos ψ − sin φ sin θ sin ψ − sin φ cos θ
− cos φ sin θ cos ψ + sin φ sin ψ cos φ sin θ sin ψ + sin φ cos ψ cos φ cos θ
HCK 3,2 .HCK 1,1 − HCK 3,1 .HCK 1,2
Rx = arctan
HCK 1,1 .HCK 2,2 − HCK 1,2 .HCK 2,1
HCK 1,3
Ry = arctan
HCK 2 + HCK 2 + HCK 2 + HCK 2
1,1 1,2 2,3 3,3
HCK 2,3 .HCK 3,1 − HCK 2,1 .HCK 3,3
Rz = arctan
HCK 2,3 .HCK 3,2 − HCK 2,2 .HCK 3,3
D. Daney INRIA Cours Robotique 200x 113 / 165](https://image.slidesharecdn.com/robotique-120802172903-phpapp01/85/Robotique-144-320.jpg)
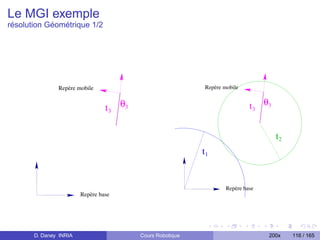
![Le Modèle Géométrique Inverse
des robots séries
X=( 0R 0 P )
0 1
Repère mobile
q4
q3
q2
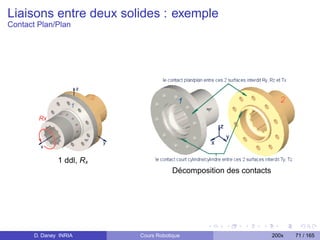
q1
Repère de base
Déterminer:
[q1 , q2 , . . . , qn ] = FMGI (X , ζ)
avec ζ les paramètres géométriques (paramètres qui définissent la
géométrie du robot série).
D. Daney INRIA Cours Robotique 200x 114 / 165](https://image.slidesharecdn.com/robotique-120802172903-phpapp01/85/Robotique-145-320.jpg)
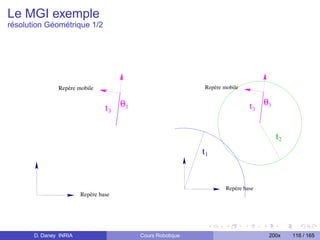
![Le MGI
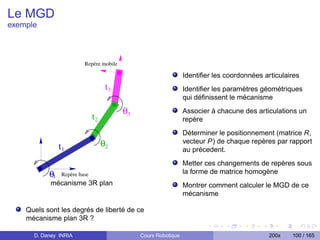
exemple
Repère mobile X = ...
3 0 1
t1 . cos θ1 + t2 . cos (θ1 + θ2 ) + t3 . cos (θ1 + θ2 + θ3 )
t3 θ3 T 2,3 @ t1 . sin θ1 + t2 . sin (θ1 + θ2 ) + t3 . sin (θ1 + θ2 + θ3 ) A
R 2,3 θ1 + θ2 + θ3
2
t2 θ T1,2 Calculer le MGI, c’est déterminer:
2
R1,2
1 [θ1 , θ2 , θ3 ] = FMGI (X1 , X2 , X3 , ζ)
t1
T 0,1 R 0,1
θ1 Repère base
avec ζ = [t1 , t2 , t3 ]
0
mécanisme 3R
plan
D. Daney INRIA Cours Robotique 200x 115 / 165](https://image.slidesharecdn.com/robotique-120802172903-phpapp01/85/Robotique-146-320.jpg)















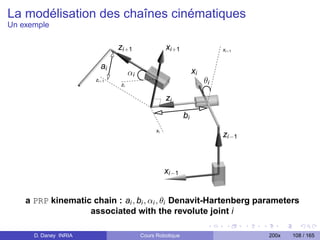
![Le MGI des robot série
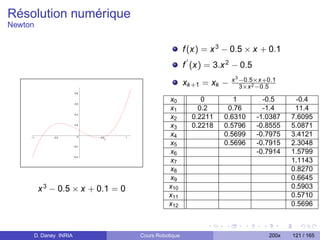
Méthode Numérique (pour les cas à problèmes)
On utilise un schéma de Newton multivarié :
Xk +1 = Xk − J −1 (XK )F (Xk )
Avec F = [f1 , . . . , fn ]T , X = [x1 , . . . , xn ]T et J la jacobienne du système
définie par :
∂f1 ∂f1 ∂f1
∂x1 ∂x2 ... ∂xn
∂f2 ∂f2 ∂f2
∂x1 ∂x2 ... ∂xn
. .
J= . .
∂f . ... ... .
n−1 . . . ∂fn−1 ∂fn−1
∂x1 ∂xn−1 ∂xn
∂fn ∂fn ∂fn
∂x1 . . . ∂xn−1 ∂xn
Attention ! ne fournit qu’une seule solution
D. Daney INRIA Cours Robotique 200x 127 / 165](https://image.slidesharecdn.com/robotique-120802172903-phpapp01/85/Robotique-165-320.jpg)

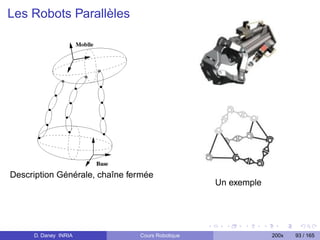
![Le cas des robots parallèles
Le MGD
„ «
P
X = = MGD(ρ, ξ)
R
Résoudre le système en P, R :
ρ1 2 − P + R.b1 + a1 2
=0
ρ2 2 − P + R.b2 + a2 2
=0
2 2
ρ3 − P + R.b3 + a3 =0
ρ4 2 − P + R.b4 + a4 2
=0
ρ5 2 − P + R.b5 + a5 2
=0
2 2
ρ6 − P + R.b6 + a6 =0
Méthodes numériques [Newton, continuation, analyse par interval]
Méthodes algébriques [Groebner, resultant]
D. Daney INRIA Cours Robotique 200x 129 / 165](https://image.slidesharecdn.com/robotique-120802172903-phpapp01/85/Robotique-167-320.jpg)
![Le cas des robots parallèles
Le MGD
„ «
P
X = = MGD(ρ, ξ)
R
Résoudre le système en P, R :
ρ1 2 − P + R.b1 + a1 2
=0
ρ2 2 − P + R.b2 + a2 2
=0
2 2
ρ3 − P + R.b3 + a3 =0
ρ4 2 − P + R.b4 + a4 2
=0
ρ5 2 − P + R.b5 + a5 2
=0
2 2
ρ6 − P + R.b6 + a6 =0
Méthodes numériques [Newton, continuation, analyse par interval]
Méthodes algébriques [Groebner, resultant]
D. Daney INRIA Cours Robotique 200x 129 / 165](https://image.slidesharecdn.com/robotique-120802172903-phpapp01/85/Robotique-168-320.jpg)
![Le cas des robots parallèles
Le MGD
„ «
P
X = = MGD(ρ, ξ)
R
Résoudre le système en P, R :
ρ1 2 − P + R.b1 + a1 2
=0
ρ2 2 − P + R.b2 + a2 2
=0
2 2
ρ3 − P + R.b3 + a3 =0
ρ4 2 − P + R.b4 + a4 2
=0
ρ5 2 − P + R.b5 + a5 2
=0
2 2
ρ6 − P + R.b6 + a6 =0
Méthodes numériques [Newton, continuation, analyse par interval]
Méthodes algébriques [Groebner, resultant]
D. Daney INRIA Cours Robotique 200x 129 / 165](https://image.slidesharecdn.com/robotique-120802172903-phpapp01/85/Robotique-169-320.jpg)
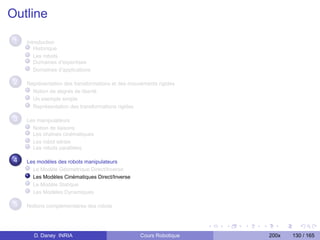





![Comment obtenir la jacobienne cinématique ?
cas spatiale
Elle passe par les calculs des vitesses de translation Vk ,n et de rotation wk ,n
˙
induites sur le repère terminal Ωn par la vitesse qk de l’articulation k ,
X = [Vk ,n , wk ,n ]T
Prismatique ˙
Vk ,n = ak qk
wk ,n = 0 (22)
Rotoïde ˙
Vk ,n = (ak ∧ Lk ,n )qk
wk ,n = ˙k
ak q (23)
avec ak le vecteur unitaire porté par l’axe zk de l’articulation k et Lk ,n le vecteur
d’origine Ok et d’extrémité On .
D. Daney INRIA Cours Robotique 200x 136 / 165](https://image.slidesharecdn.com/robotique-120802172903-phpapp01/85/Robotique-176-320.jpg)






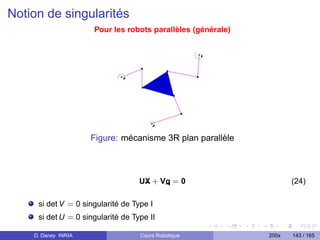




![Espace de travail, définitions et problématique
Définitions
Soit, Q, l’espace articulaire définie par :
Q = {q = [q1 , . . . , qn ]|qi Min ≤ qi ≤ qi Max , ∀i = 1, . . . , n}
L’espace de travail (W ) d’un robot est l’image de Q par le modéle
géométrique direct :
W = FMGD (Q)
D. Daney INRIA Cours Robotique 200x 150 / 165](https://image.slidesharecdn.com/robotique-120802172903-phpapp01/85/Robotique-190-320.jpg)
![Espace de travail, définitions et problématique
Définitions
Soit, Q, l’espace articulaire définie par :
Q = {q = [q1 , . . . , qn ]|qi Min ≤ qi ≤ qi Max , ∀i = 1, . . . , n}
L’espace de travail (W ) d’un robot est l’image de Q par le modéle
géométrique direct :
W = FMGD (Q)
D. Daney INRIA Cours Robotique 200x 150 / 165](https://image.slidesharecdn.com/robotique-120802172903-phpapp01/85/Robotique-191-320.jpg)





![Propriété des robots
De nombreuses propriétés associées aux robots sont quantifié à travers
l’évaluation de valeurs propres (solution de det(J − σ.I) = 0 → [σ1 . . . σn ] )
. ...dq ... ∆ q .
q 1 1
1 X
J
σ2
.
1 q σ1
2
Singularité, Précision , Isotropie → dextérité ...
D. Daney INRIA Cours Robotique 200x 154 / 165](https://image.slidesharecdn.com/robotique-120802172903-phpapp01/85/Robotique-197-320.jpg)