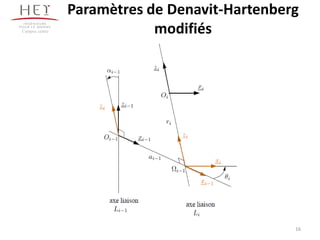
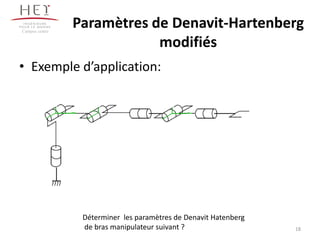
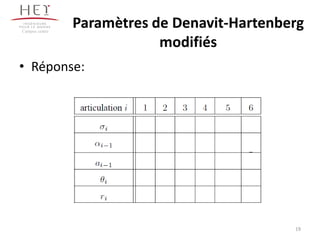
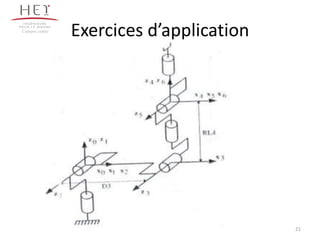
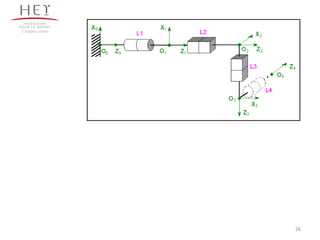
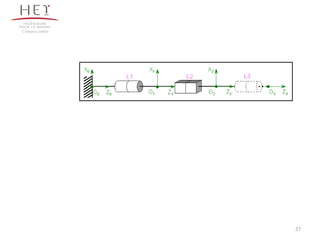
Le chapitre 3 se concentre sur la morphologie des bras manipulateurs, en abordant les mécanismes, la chaîne cinématique et les paramètres de Denavit-Hartenberg. Il décrit les différents types d'articulations et leurs représentations ainsi que les architectures en série et parallèle. Le document propose également des exercices d'application pour illustrer les concepts présentés.

1. Chapitre 3
Les bras manipulateurs
Campus centre
1
Mouna Souissi
Mouna.souissi@hei.fr

2. Plan
1. Morphologie des robots manipulateurs
2. Chaine cinématique d’un bras manipulateur
3. Paramètres de Denavit-Hartenberg modifiées
 Convention
 Principe
 Hypothèses
 Applications
Campus centre
2

3. Morphologie des robots
manipulateurs
Mécanisme = un ensemble de solides reliés 2 à 2 par des liaisons
Il existe 2 types de mécanismes:
Campus centre
mécanismes en chaîne simple
ouverte
mécanismes en chaîne
complexe
3

4. Morphologie des robots
manipulateurs
• Pour représenter un mécanisme, on dispose de 2 méthodes :
• Le schéma cinématique : On utilise la représentation
normalisée des liaisons pour représenter le mécanisme, soit
en perspective, soit en projection.
• Le graphe, non normalisé.
• Exemple :
• Graphe de liaison d’un robot mobile
Campus centre
4

5. Morphologie des robots
manipulateurs
• Afin de dénombrer les différentes architectures possibles, on
ne considère que 2 paramètres : le type d'articulation (rotoïde
(R) ou prismatique (P)) et l'angle que font deux axes
articulaires successifs.
Campus centre
5
Glissières (prismatic,P-joint) Pivots (revolute, R-joint)

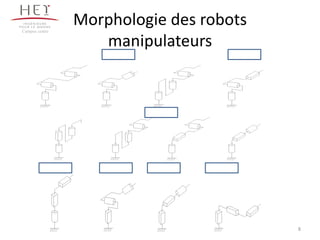
6. Morphologie des robots
manipulateurs
Campus centre
6
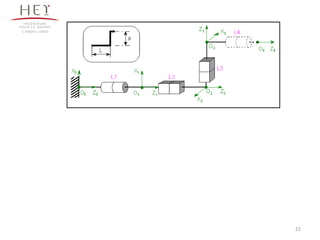
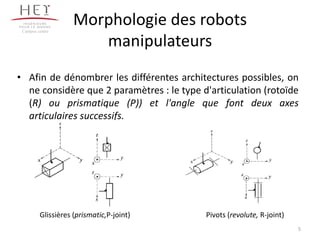
Articulation prismatique, noté P
1 ddl en translation Tx .
Valeur articulaire q = longueur [m].
Articulation rotoïde, noté R
1 ddl en rotation Rx .
Valeur articulaire q = angle [rad], [].

7. • Chaine cinématique :
7
Morphologie des robots
manipulateurs
Campus centre

8. Morphologie des robots
manipulateurs
Campus centre
8

9. Morphologie des robots
manipulateurs
Architecture série Architecture parallèle
Mécanisme en chaîne cinématique
ouverte constitué d’une alternance de corps et
de liaisons.
Mécanisme en chaîne cinématique fermée
dont l'organe terminal est relié à la base par
plusieurs chaînes cinématiques
indépendantes.
Campus centre
9

10. Morphologie des robots
manipulateurs
• Espace de travail:
Campus centre
10

11. Morphologie des robots
manipulateurs
• Espace de travail:
Campus centre
11

12. Chaine cinématique d’un bras
manipulateur
• On supposera par la suite les bras manipulateurs constitués
de n corps mobiles reliés entre eux par n liaisons rotoides et
ou prismatiques formant une structure de chaine simple.
• Pour identifier la nature de la i-ème liaison du bras
manipulateur, on définit le paramètre:
σi=
Campus centre
12
0 pour une liaison rotoide
1 pour une liaison prismatique

13. Chaine cinématique d’un bras
manipulateur
Campus centre
13
Un bras manipulateur est la succession des liaisons.

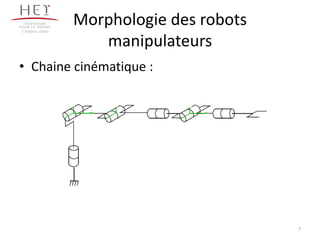
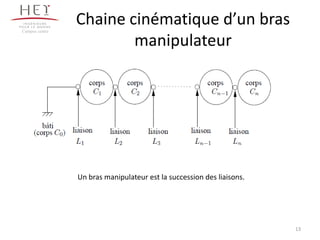
14. Chaine cinématique d’un bras
manipulateur
Campus centre
14
 Coordonnées généralisé X = [P,R]
(position P / orientation R)
 Coordonnées articulaire q
(consignes données aux moteurs : soit rotation autour d’un axe soit
translation suivant un axe)
 Paramètres géométriques Ϛ qui définissent de façon statique les dimension
du robot

15. Paramètres de Denavit-Hartenberg
modifiés
• Selon cette convention, chaque transformation est
représentée comme le produit de quatre
transformations basiques.
• Li une liaison rotoïde ou prismatique parfaite c’est-à-dire suivant un
seul axe, donc représentée par un seul paramètre.
• (Oi , xi , yi , zi ) le repère lié à la liaison i.
• Oi−1
• xi−1
• zi−1
• yi−1
Campus centre
15

16. 16
Paramètres de Denavit-Hartenberg
modifiésCampus centre

17. Paramètres de Denavit-Hartenberg
modifiés
Campus centre
17
• Chaque transformation entre deux corps successifs est donc
décrite par quatre paramètres :
• αi-1:
• ai-1:
• Өi :
• Ri :

18. • Exemple d’application:
Campus centre
18
Paramètres de Denavit-Hartenberg
modifiés
Déterminer les paramètres de Denavit Hatenberg
de bras manipulateur suivant ?

19. • Réponse:
Campus centre
19
Paramètres de Denavit-Hartenberg
modifiés

20. • Relation géométrique :
• La matrice de rotation entre les corps Ci-1 et Ci est :
Campus centre
20
Paramètres de Denavit-Hartenberg
modifiés

21. Exercices d’applicationCampus centre
21

22. Campus centre
22

23. Campus centre
23

24. 24
Campus centre

25. 25
Campus centre

26. 26
Campus centre

27. 27
Campus centre