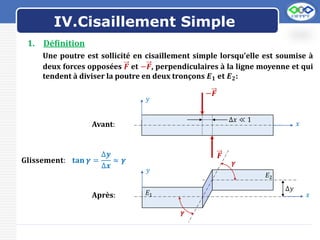
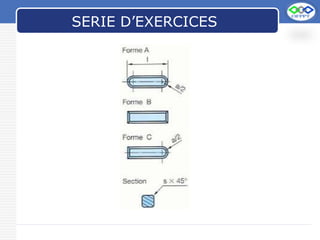
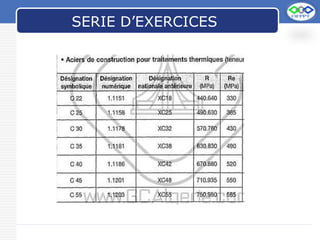
Le document traite du cisaillement simple des poutres, définissant les contraintes tangentiels et établissant la loi de Hooke en cisaillement. Il souligne que la contrainte doit rester inférieure à la résistance admissible au cisaillement du matériau et présente une analogie avec la traction. Des exemples de valeurs pour divers matériaux et des exercices pratiques sont également fournis.