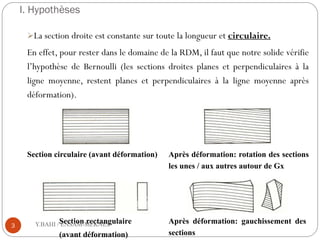
Le document traite de la torsion pure en résistance des matériaux, décrivant les hypothèses et conditions de déformation pour les poutres soumises à un moment de torsion. Il établit des relations entre contraintes, déformations, et présente des conditions de dimensionnement basées sur la contrainte tangentielle admissible. Enfin, il lie la puissance à la torsion par l'équation de la puissance en fonction du moment de torsion.

1. Chapitre 5:
Torsion pure
Résistance Des
Matériaux
1 Y.BAHI / ENSAM-MEKNES

2. I. Hypothèses
➢ Le solide est composé d’un matériau homogène et isotrope,
➢ Sa ligne moyenne est rectiligne,
➢ Les actions extérieures dans les sections extrêmes sont modélisables par
deux moments opposés portés par la ligne moyenne.
2 Y.BAHI / ENSAM-MEKNES

3. I. Hypothèses
➢La section droite est constante sur toute la longueur et circulaire.
En effet, pour rester dans le domaine de la RDM, il faut que notre solide vérifie
l’hypothèse de Bernoulli (les sections droites planes et perpendiculaires à la
ligne moyenne, restent planes et perpendiculaires à la ligne moyenne après
déformation).
Section circulaire (avant déformation) Après déformation: rotation des sections
les unes / aux autres autour de Gx
Section rectangulaire
(avant déformation)
Après déformation: gauchissement des
sections
3 Y.BAHI / ENSAM-MEKNES

4. II. Définition
Une poutre est sollicitée à la torsion pure si le seul élément de réduction
au centre de gravité de chaque section des forces de cohésion est un moment
autour de la ligne moyenne appelé moment de torsion.
 N=Ty=Tz=0 , Mfy=Mfz=0 , Mt0
4 Y.BAHI / ENSAM-MEKNES

5. III. Etude des déformations
Essai de torsion
Soit une poutre circulaire pleine, parfaitement encastrée en S0 (section de
référence), soumise à l’extrémité S1 à un moment de torsion Mt:
M0
M M1
(S0) (S1)
(S)
l
l1
M’ M1’
a a1
Mt
M
M’
a
G
L’expérience montre que, pour une
section et un moment de torsion
donnés, on a :
cste
=
=
a
=
a
...
1
1


➢q:angle de torsion unitaire (rad/mm)
➢a: angle total de torsion de (S)/(S0) (rad)
➢l: distance entre (S) et (S0) (mm)
On pose :

a
=
q
5 Y.BAHI / ENSAM-MEKNES
M M1

6. III. Etude des déformations
➢Si Mt<MA, on est dans le domaine
élastique, l’angle a est proportionnel au
moment appliqué
➢Si Mt>MA, on est dans le domaine
plastique, l’angle a n’est plus
proportionnel au moment appliqué
Mt
MA
(S0) (S1)
(S)
l
l1
M0
M M1
M’
M1’
a
On appelle g, l’angle MM0M’. Cet
angle représente l’angle de glissement
de (S)/(S0) (ou distorsion).
On a :
g

g
=
= tg
MM'
MM
MM'
0 
6 Y.BAHI / ENSAM-MEKNES

7. III. Etude des déformations
En torsion, les sections du solide sont soumises à une contrainte tangentielle
(ou de cisaillement). la relation liant les contraintes et les déformations:
q

=
a

=
=
g .
.


MM'
M
M’
a
G

g
=
 .
G
On obtient donc:

q
=
 .
.
G
Avec:
 : la contrainte de cisaillement,
G : le module de Coulomb,
q : angle unitaire de torsion,
 : distance du point considéré à l’axe Gx.
7 Y.BAHI / ENSAM-MEKNES

8. IV. Etude des contraintes
On coupe le cylindre en une section (S) et on exprime que la partie isolée est
en équilibre sous l’action du moment de torsion Mt et des forces de cohésion
dans la section (S).
 

= S
.
. dS
Mt
G
r

dS
dS : élément de surface situé à une distance  de
l’axe Gx, soumis à une contrainte de cisaillement 
L’effort élémentaire de cisaillement dF vaut donc:
dS
dF .

=
L’équilibre de l’élément isolé s’écrit donc:
Or : 
q
=
 .
.
G
D’où :  q

= S
.
.
G
². dS
Mt
Comme G.q est identique pour chaque dS, on obtient finalement :
 
q
= S
².
.
.
G dS
Mt 0
t I
M .
.
G q
=


Moment d’inertie polaire
de (S)/ à G
8 Y.BAHI / ENSAM-MEKNES

9. IV. Etude des contraintes
On sait aussi que :
max
max
max
max

q
=
 .
.
G
0
t
I
M
.

=

On peut donc exprimer la contrainte de cisaillement en fonction de Mt,
on obtient:
0
t I
M .
.
G q
=
On a donc :
La contrainte de cisaillement est donc proportionnelle à la distance / au
c.d.g. de la section et est maximale pour  = r :
0
t
max
I
M
r.
=

)
(mm
torsion
de
module
:
r
I 3
0
9 Y.BAHI / ENSAM-MEKNES

10. V. Dimensionnement
V.1 Condition de résistance
Le dimensionnement des solides soumis à la torsion pure se fera en
limitant la valeur de la contrainte tangentielle à une valeur notée Rpg
(résistance pratique au glissement = contrainte tangentielle
admissible adm) définie par :
s
Rpg
e

=
On obtient ainsi l’inéquation (d’équarrissage) suivante:
pg
0
t
max R
.r
I
M

=

Limite élastique au
cisaillement
Coefficient de sécurité
10 Y.BAHI / ENSAM-MEKNES

11. V. Dimensionnement
V.2 Condition de déformation
On utilise souvent l’angle limite de torsion pour dimensionner une
pièce soumise à la torsion (surtout dans le cas d’arbres de grande
longueur).
On obtient ainsi l’inéquation suivante:
lim
0
t
lim
0
t
G.I
M
ou
G.I
M
a

=
a
q

=
q

.
11 Y.BAHI / ENSAM-MEKNES

12. VI. Relation entre puissance et moment de torsion

= .
M
P t
Avec :
P : puissance en Watts
Mt : moment de torsion en N.m
 : vitesse angulaire en rad/s
Si la vitesse de rotation est donnée en tours/min, il faut convertir :
60
.
.
2 n

=

12 Y.BAHI / ENSAM-MEKNES