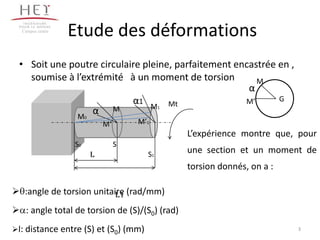
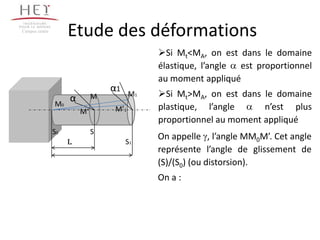
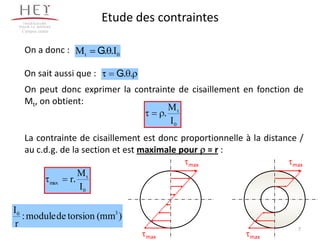
Le chapitre traite de la torsion pure subie par une poutre, définie par un moment de torsion autour de son axe neutre. Il explique les concepts d'angle de torsion, de contraintes de cisaillement et de conditions de dimensionnement pour garantir la résistance des solides soumis à la torsion. L'accent est mis sur les relations entre les moments de torsion, les contraintes et les déformations, ainsi que sur les critères pratiques pour la conception d'éléments tournants.

1. Campus centre
Chapitre 7
Torsion pure
1

2. Campus centre
Définition
Une poutre est sollicitée à la torsion pure si le seul élément de
réduction au centre de gravité de chaque section des forces de
cohésion est un moment autour de la ligne moyenne appelé moment
de torsion.
N=Ty=Tz=0 , Mfy=Mfz=0 , Mt 0
M M
G
A B
L
2

3. Campus centre
Etude des déformations
• Soit une poutre circulaire pleine, parfaitement encastrée en ,
soumise à l’extrémité à un moment de torsion M
α
.G
α1 M1 Mt M’
M0
α M
M’ M’1
L’expérience montre que, pour
S0 S
l S1 une section et un moment de
torsion donnés, on a :
 :angle de torsion unitaire (rad/mm)
l1
 : angle total de torsion de (S)/(S0) (rad)
l: distance entre (S) et (S0) (mm) 3

4. Campus centre
Etude des déformations
Si Mt<MA, on est dans le domaine
élastique, l’angle est proportionnel
au moment appliqué
α1
α M M1 Si Mt>MA, on est dans le domaine
M0 plastique, l’angle n’est plus
M’ M’1
proportionnel au moment appliqué
S0 S
On appelle , l’angle MM0M’. Cet angle
l S1
représente l’angle de glissement de
(S)/(S0) (ou distorsion).
On a :

5. Campus centre
Etude des déformations
En torsion, les sections du solide sont soumises à une contrainte
tangentielle (ou de cisaillement). Nous avons vu (cf. chapitre VI) la
relation liant les contraintes et les déformations:
On obtient donc:
Avec:
: la contrainte de cisaillement,
G : le module de Coulomb,
: angle unitaire de torsion,
: distance du point considéré à l’axe Gx. 5

6. Campus centre
Etude des contraintes
On coupe le cylindre en une section (S) et on exprime que la partie
isolée est en équilibre sous l’action du moment de torsion Mt et des
forces de cohésion dans la section (S).
dS : élément de surface situé à une distance de
r dS l’axe Gx, soumis à une contrainte de cisaillement
G
L’effort élémentaire de cisaillement dF vaut donc:
dF .dS
L’équilibre de l’élément isolé s’écrit donc: Mt S
. .dS
Or : G. .
D’où : M t S
².G. .dS
Comme G. est identique pour chaque dS, on obtient finalement :
Mt G. . ².dS Mt G. .I0 Moment d’inertie
S polaire
6
de (S)/ à G

7. Etude des contraintes
Campus centre
On a donc : Mt G. .I0
On sait aussi que : G. .
On peut donc exprimer la contrainte de cisaillement en fonction de
Mt, on obtient:
Mt
.
I0
La contrainte de cisaillement est donc proportionnelle à la distance /
au c.d.g. de la section et est maximale pour = r :
max max
Mt
max r.
I0
I0
: module de torsion (mm3 )
r 7
max max

8. Campus centre
Dimensionnement
Condition de résistance
Le dimensionnement des solides soumis à la torsion pure se fera en
limitant la valeur de la contrainte tangentielle à une valeur notée Rpg
(résistance pratique au glissement = contrainte tangentielle
admissible adm) définie par :
On obtient ainsi l’inéquation (d’équarrissage) suivante:
8

9. Campus centre
Dimensionnement
Condition de déformation
On utilise souvent l’angle limite de torsion pour dimensionner une
pièce soumise à la torsion (surtout dans le cas d’arbres de grande
longueur). Mt
lim
On obtient ainsi l’inéquation suivante: G.I 0
ou
M t .
lim
G.I 0
P Mt .
Avec : P : puissance en Watts
Mt : moment de torsion en N.m
: vitesse angulaire en rad/s
Si la vitesse de rotation est donnée en tours/min, il faut convertir :
2. .n
60
9