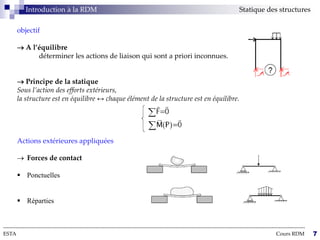
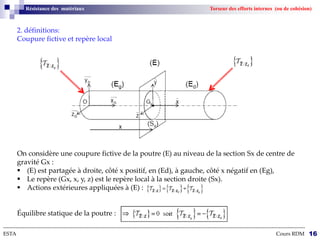
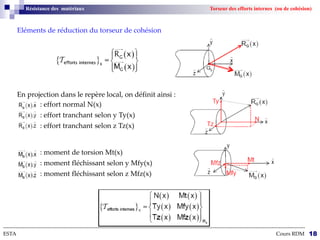
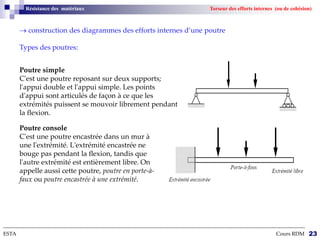
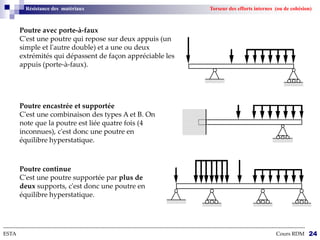
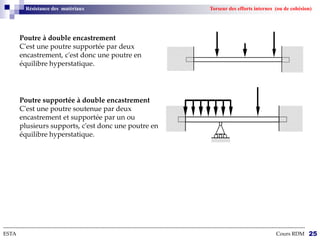
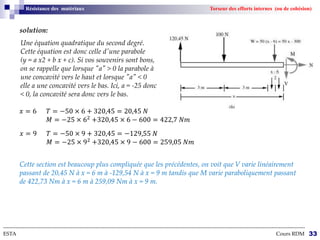
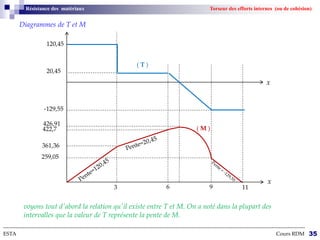
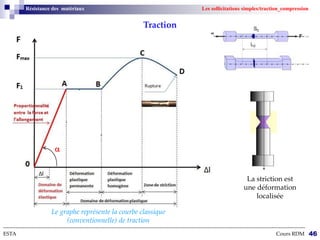
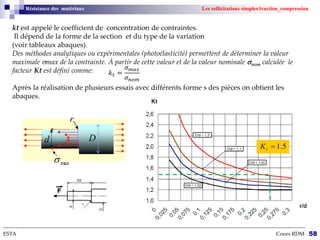
Le cours sur la résistance des matériaux traite des effets des actions extérieures sur des structures, en se concentrant sur le comportement des poutres sous différentes charges. L'objectif est de dimensionner et vérifier des pièces de machinerie, avec un accent particulier sur l'aéronautique, où la fiabilité des composants est cruciale. Les notions de forces, déformations, et contraintes sont expliquées à travers des hypothèses et théories de la mécanique des milieux continus.