Le document traite de la flexion simple des sections, définissant les forces et moments en jeu, notamment dans les sections rectangulaires sans armature comprimée. Il explique les méthodes pour déterminer les armatures nécessaires, en tenant compte des caractéristiques du béton et de l'acier, ainsi que des conditions limites. Il aborde également des applications numériques pour illustrer le calcul des moments fléchissants et des armatures dans les poutres soumises à des charges.



![sd
M
A
σβ ⋅⋅
=
²].[en:
][:
][en:et
][:
cmA
MPaenet
cmdb
MPaenM
sb σσ
Remarque :
Théoriquement ; la méthode déjà exposée est valable jusqu’à ce que l’on ait
dy = c’est à dire 1=α ou bien 480.0=µ mais pratiquement il n’en ait pas ainsi car à
partir d’une certaine valeur de sξ , donc de α , la contrainte sσ diminue rapidement et
on arrive à une section qui n’est pas économique.
Si 01
1
1000
5.3
1 =
−=⇒=
α
ξα s , d’où
0=⋅= sss E ξσ et ∞→A d’où de point de
vue économie, il a été décidé que
ss
Ls
E
fe
⋅
=≥
γ
ξξ
Et LLL βαξ ,→ et Lµ .
Et on a : ⇒
+
=
sξ
α
10005.3
5.3
L
L
ξ
α
10005.3
5.3
+
= ;
( )LLL ααµ 4.018.0 −⋅⋅= et LL αβ 4.01−=
Et dans le chapitre N°01 on a vue que :
Si
≤
≤
⇒≥
L
L
Ls
αα
µµ
ξξ
Si →≤ Lµµ la section sera armé uniquement par des armatures tendues.
Si →> Lµµ la section sera armé par des armatures tendues et des
armatures comprimées comme il va être montré par la suite.
sσ
0 Lξ sξ
s
s
fe
σ
γ
=
10%o](https://image.slidesharecdn.com/chapitre04-160902213842/85/Chapitre-04-flexion-simple-4-320.jpg)


![1. Première méthode de détermination des armatures :
A′ : Section totale des armatures comprimées.
d⋅′δ : distance du centre de gravité des armatures comprimées à la fibre la
plus comprimée. (en pratique on prend hd
10
1
=⋅′δ ).
La section envisagée (figure a) peut être considérée comme la somme de
deux section fictives représentées sur les figures (b) et (c).
′=′
+=
AA
AAA 21
les armatures comprimées sont nécessaires ⇒ domaine 2 et le diagramme
des déformations passe par le pivot B.
pour des raisons d’économie, sξ doit être supérieur ou égal à Lξ et pour un
cas limite, on prend Ls ξξ = ; d’où :
L
L
ξ
α
10005.3
5.3
+
= et
ss
L
E
fe
⋅
=
γ
ξ .
Et en utilisant les triangles semblables ccG ′ˆ et aaG ′ˆ , on trouve :
( )
L
L
L
L
L
L
L
s
dd
dd
yd
dy
ξ
δξδ
α
δα
α
δαδ
ξ
ξ
⋅
′⋅−′−
=
−
′−
=
⋅−
⋅′−⋅
=
−
′−
=
′
1000
100015.3
1
, d’où
( ) δξδξ ′⋅⋅−′−=′ Ls 100015.31000
et pour que Ls ξξ ≥′ , il faut
que ( ) ⇒≥′⋅−′− LL ξδξδ 1000100015.3
L
L
ξ
ξ
δ
10005.3
10005.3
+
⋅−
≤′
pour chaque type d’acier on a une valeur de ⇒Lξ pour chaque type d’acier
on a une valeur de δ ′ à ne pas dépasser [voir tableau ci-après].
Ronds lisses Haute adhérence
Fe E215 Fe E235 Fe E400 Fe E500
15.1=sγ 1=sγ 15.1=sγ 1=sγ 15.1=sγ 1=sγ 15.1=sγ 1=sγ
0.58 0.53 0.55 0.50 0.33 0.27 0.23 0.17
A
d
b
A′
(a)
d⋅′δ
sξ′
o%5.3
d⋅′δ
dy L ⋅=α
a′ a
G
c c′
b
A1
d
b
(b)
A2
A′
(c)
dd ⋅′−δ
B](https://image.slidesharecdn.com/chapitre04-160902213842/85/Chapitre-04-flexion-simple-7-320.jpg)

![Soit une section rectangulaire avec armatures comprimées (Fig (a)) et
soumises à un moment de flexion M. les figures (b) et (c) représentent
respectivement les diagrammes et des contraintes.
On a bb ybF σ⋅⋅⋅= 8.0 sa AF σ ′⋅′=′ sa AF σ⋅=
Avec dy L ⋅=α
Equations d’équilibre :
08.000/ =⋅⋅⋅−′′−⇒=′−−⇒=∑ ybAAFFFF bssabaH σσσ
s
bs ybA
A
σ
σσ
′
⋅⋅⋅−⋅
=′⇒
8.0
( ) ( ) ⇒=′−+⋅′−−⇒=∑ 04.00/ dyFddFMM bac δδ
( ) ( ) ⇒=′−⋅⋅⋅+′−⋅− 04.08.0 dyybddAM bs δσδσ
( )
( )dd
dyybM
A
s
b
δσ
δσ
′−
′−⋅⋅⋅+
=
4.08.0
M : en [N.m], b, d et y en [cm], sb σσ , et sσ ′ en [Mpa]
A et A′ : en [cm²].
ApplicationApplicationApplicationApplication ::::
Soit la poutre représentée sur la figure ci-dessous, soumise à son poids
propre (g) et à une surcharge d’exploitation Q= 264 KN.
Acier Fe E400.
MPafc 2528 =
Calcul du moment fléchissant :
8
²l
gMG = avec mlKNhbg b /5.46.03.025 =⋅⋅=⋅⋅= γ
mKNMG .78.13
8
²5
5.4 ==
mKN
l
QMQ .330
4
5
264
4
=⋅=⋅=
mKNMMM QG .5143305.178..1335.15.135.1 =⋅+⋅=+=
5 cm
A
60
30
5 cm
A′
g
2.50 2.50
Q](https://image.slidesharecdn.com/chapitre04-160902213842/85/Chapitre-04-flexion-simple-9-320.jpg)

![( ) ( )
²52.0
555348
8849
2 cm
dd
M
A
s
=
−
=
′−⋅
∆
=
δσ
09.0
55
5
===′
d
c
δ ;
34.0
739.15.3
739.15.3
10005.3
10005.3
?
=
+
−
=
+
−
≤′
L
L
ξ
ξ
δ
MPa
fe
s
s
sLs 34834.009.0 ===′⇒>′⇒< σ
γ
σξξ donc
( ) ( )
²52.0
555348
8849
2 cm
dd
M
AA
s
=
−
=
′−′
∆
==′
δσ
et enfin :
=+=
=′
²52.36
52.0
21
2
cmAAA
cmA
Remarque :
Si sss
L
L
E ξσ
ξ
ξ
δ ′⋅=′⇒
+
⋅−
>′
10005.3
10005.3
(car Ls ξξ <′ ).
2ème
méthode (méthode des diagramme).
∃′⇒=>= AL 392.0399.0 µµ
cmdy L 74.3655668.0 =⋅=⋅=α
( )
( )
( )
( )555348
574.364.074.36302.148.5140004.08.0
−
−⋅⋅⋅⋅⋅+
=
′−
′−⋅⋅⋅+
=
dd
dyybM
A
s
b
δσ
δσ
²52.36 cmA =
L
L
ξ
ξ
δ
10005.3
10005.3
?
+
−
≤′ ; MPa
fe
s
sLs 34834.009.0 ==′⇒>′⇒≤
γ
σξξ
²52.0
348
74.36302.148.034852.368.0
cm
ybA
A
s
bs
=
⋅⋅⋅−⋅
=
′
⋅⋅⋅−⋅
=′
σ
σσ
²52.0 cmA =′
Rappels (Flexion simple).Rappels (Flexion simple).Rappels (Flexion simple).Rappels (Flexion simple).
Si 5293.00 ≤≤α c’est à dire →≤≤ 186.00 µ le diagramme des déformations
passe par le pivot A (domaine 1) [ ]os %10=ξ , c’est à dire
s
s
fe
γ
σ = .](https://image.slidesharecdn.com/chapitre04-160902213842/85/Chapitre-04-flexion-simple-11-320.jpg)
![Si 12593.0 ≤<α c’est à dire →≤< 480.0186.0 µ le diagramme des
déformation passe par le pivot B (domaine 2) [ ]ob %10≤ξ ; donc on peut avoir deux
cas :
- Si Lµµ ≤ (c’est à dire Ls ξξ ≥ )
s
s
fe
γ
σ =→
- Si Lµµ > (c’est à dire Ls ξξ < ) ( )ssss E ξξσ 1000200=⋅=→
Avec
−= 1
1
5.31000
α
ξs
Remarque :
- Si Lµµ > (donc Ls ξξ < ) la section d’armatures calculée ne sera pas économique,
et pour remédier à cela on utilise des armatures comprimées ; donc :
Si ∃′⇒> ALµµ et
=≥
s
sLs
fe
γ
σξξ et aussi pour que
=′≥′
s
sLs
fe
γ
σξξ il
faut que :
L
L
ξ
ξ
δ
10005.3
10005.3
+
−
≤′
si ( )sssss
L
L
EL
ξξσξξ
ξ
ξ
δ ′=⋅=′⇒<′⇒
+
−
>′ 1000200
10005.3
10005.3
.
Raccourcissement des armatures compriméesRaccourcissement des armatures compriméesRaccourcissement des armatures compriméesRaccourcissement des armatures comprimées ::::
a. Diagramme des déformations passe par le point A :
%10=sξ o
Les triangles AaGˆ et ccG ′ˆ sont semblables
⇒
dd
dd
Ga
Gc
aA
cc s
α
δαξ
−
′−⋅
=
′⋅
⇒=
′
10
1000
⇒
−
′−
=′
α
δα
ξ
1
101000 s
le raccourcissement sξ′1000 étant connu, la
contrainte sσ ′ dans l’armature comprimée a pour valeur :
- Si ( )ssLs ξσξξ ′⋅=′→<′ 100020010001000 ; sσ ′ en [Mpa].
- Si
s
sLs
fe
γ
σξξ =′→≥′ 10001000
A a
b
d
10 %o
B
c
G
sξ′dy ⋅=α
3.5 %o
dδ ′
c’](https://image.slidesharecdn.com/chapitre04-160902213842/85/Chapitre-04-flexion-simple-12-320.jpg)




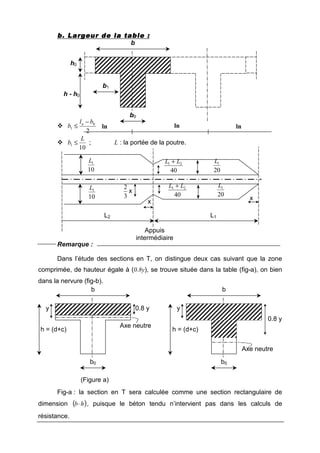

![Fb2 :la résultante des efforts de compression sur la partie doublement
hachurée appliquée à (0.4y) de l’arrête supérieure.
Fa :la résultante des efforts de traction dans les armatures tendues.
Bilans des efforts :
( ) 001 hbbF bb −⋅= σ ; ybF bb ⋅⋅⋅= 02 8.0 σ et sa AF σ⋅=
Equations d’équilibre :
( ) 08.000 00021/ =⋅⋅⋅−⋅−−⋅⇒=−−⇒=∑ ybhbbAFFFF bbsbbaH σσσ
( ) ( )∑ =−⋅⋅⋅⋅−
−⋅−−⇒= 04.08.0
2
0 0
0
00/ ydyb
h
dhbbMM bba σσ
posons : ( )
−⋅⋅−⋅−=
2
0
00
h
dhbbMMn bσ et ⇒⋅= dy α
( ) ( ) 04.018.04.08.0 2
00 =−⋅⋅⋅⋅⋅−=−⋅⋅⋅⋅− αασσ dbMydybM bnbn
avec ( ) 2
0
4.018.0
db
M
b
n
⋅⋅
=⇒−⋅⋅=
σ
µααµ
Et on a : ( ) ⇒=⋅⋅⋅−⋅−⋅−⋅ 08.0 000 ybhbbA bbs σσσ
( ) 0008.0 hbbAyb bsb ⋅−⋅−⋅=⋅⋅⋅ σσσ
et ( ) ⇒=⋅−⋅⋅⋅⋅− 04.08.0 0 ydybM bn σ
( )[ ] ( ) ⇒=−⋅⋅−⋅−⋅− 04.000 ydhbbAMn bs σσ
( )[ ] ( ) ⇒=⋅−⋅⋅−⋅−⋅− 04.0100 dhbbAMn bs ασσ
( )[ ] 000 =⋅⋅⋅−⋅−⋅− dhbbAMn bs βσσ car αβ 4.01−=
donc :
( )
s
b
n
hbb
d
M
A
σ
σ
β
00 ⋅−⋅+
⋅
=
RésuméRésuméRésuméRésumé ::::
- Si →
−⋅⋅⋅=>
2
0
00
h
dhbMM bσ axe neutre dans la nervure et la section de
calcul est une section en T.
- ( )
−⋅⋅−⋅−=
2
0
00
h
dhbbMM bn σ
ss
b
n
db
M
σξβα
σ
µ →⇒
⋅⋅
= 1000,,2
0](https://image.slidesharecdn.com/chapitre04-160902213842/85/Chapitre-04-flexion-simple-19-320.jpg)
![( )
⇒
⋅−⋅+
⋅
=
s
b
n
hbb
d
M
A
σ
σ
β
00
( ) ⇒
⋅⋅
⋅⋅⋅−⋅+
=
s
bn
d
dhbbM
A
βσ
βσ 00
M et Mn en [MPa] ; b, b0,, h0 et d en [cm] ; ][:enet MPasb σσ A : en [cm²].
Application numérique N°01Application numérique N°01Application numérique N°01Application numérique N°01 ::::
Acier Fe E400
MPafc 2028 =
prendre en compte le poids propre g.
Ferraillage de la section la plus sollicitée :
Calcul du moment maximum :
( ) mlKNmlKNSg bb /5.5/5505.02.0112.02500 ==⋅+⋅⋅=⋅= γ
mKN
l
gM g .2.17
8
²5
5.5
8
2
=⋅==
mKN
l
QMQ .135
4
5
108
4
=⋅== .
Combinaison fondamentale :
QG 5.135.1 +
⇒⋅+⋅=⋅+⋅= 35.15.12.1735.15.135.1 Qg MMM
mKNM .72.225= .
Vérification de la position de l’axe neutre :
Moment résistant de la table :
−⋅⋅⋅==
2
0
00
h
dhbMM bT σ
avec
b
c
b
f
γ
σ 2885.0 ⋅
=
MPab 33.11=σ
( )⇒−⋅⋅⋅= 6451212033.11TM
20
5
12
50
120
2.50 2.50
Q=108 KNg
b0
b
0.8y= h0
. cm
h
c 5
10
==](https://image.slidesharecdn.com/chapitre04-160902213842/85/Chapitre-04-flexion-simple-20-320.jpg)
![mKNmKNMT .3.636.103.636 3
=⋅=
TMM < : L’axe neutre tombe dans la table ⇒ la section en T sera calculée
comme une section rectangulaire de dimension [120 x 50] cm².
Vérification de l’existence de A′ :
( )
082.0
4512033.11
1072.225
² 2
3
=
⋅⋅
⋅
=
⋅⋅
=
db
M
bσ
µ
Acier Fe E400 0392=→ Lµ donc :
∃′⇒< ALµµ et MPa
fe
s
sLs 34810001000 ==⇒>
γ
σξξ
0
8.0
211
=
−−
=
µ
α ; 957.04.01 =−= αβ
²06.15
45957.0348
1072.225 3
cm
d
M
A
s
=
⋅⋅
⋅
=
⋅⋅
=
βσ
²06.15 cmA = .
Application N° 02.Application N° 02.Application N° 02.Application N° 02.
Ferrailler la section la plus solliciter de la poutre suivante :
Acier Fe E400
MPafc 2528 =
prendre en compte le poids propre de la poutre g.
Ferraillage de la section la plus sollicitée :
Poids propre :
( ) ./5.5/5505.02.0112.02500 mlKNmlKgSg bb ==⋅+⋅⋅=⋅= γ
Moment fléchissant maximum :
mK
l
gM g .2.17
8
²5
5.5
8
²
=⋅=⋅=
mK
l
QMQ .525
4
5
420
4
=⋅=⋅=
20
5
12
50
120
2.50 2.50
Q=420 KNg](https://image.slidesharecdn.com/chapitre04-160902213842/85/Chapitre-04-flexion-simple-21-320.jpg)


![RésuméRésuméRésuméRésumé ::::
Si ∃′⇒> ALµµ
( )
−⋅⋅−⋅+⋅⋅⋅=
2
0
00
2
01
h
dhbbdbM bbL σσµ
1MMM −=∆
( )
s
L
L
s σ
α
δα
ξ ′→
′−
=′
5.3
1000
s
sLs
fe
γ
σξξ =→=
( )dd
M
A
s δσ ′−⋅′
∆
=′ ;
( )
s
s
s
b
L
bL
A
hbb
d
db
A
σ
σ
σ
σ
β
σµ
′
′+
⋅−⋅+
⋅
⋅⋅⋅
=
00
0
1
²
M et M1 M∆ en [MPa] ; b, b0,, h0 et d en [cm] ; ][:enet, MPassb σσσ ′ A et A′ :
en [cm²].
ApplicationApplicationApplicationApplication ::::
Calculer le ferraillage de la section la plus sollicitée de la poutre suivante :
Acier Fe E400
MPafc 2028 = .
Prendre en compte le poids propre g.
mlKNg /5.5=
Moment fléchissant :
mKN
l
QMQ .585
4
5
468
4
=⋅=⋅=
mKNM g .19.17=
combinaison fondamentale :
mKNMMM Qg .7.9005.135.1 =+⋅=
20
5
12
50
120
2.50 2.50
Q=468 KNg](https://image.slidesharecdn.com/chapitre04-160902213842/85/Chapitre-04-flexion-simple-24-320.jpg)
