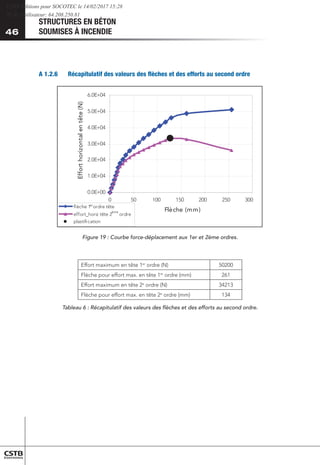
Ce document présente un guide sur le calcul de la résistance des ossatures en éléments industrialisés en béton face aux séismes, conformément aux normes Eurocode 8. Il propose des méthodes de dimensionnement adaptées aux bâtiments à un seul niveau ou avec mezzanines, en détaillant la vérification des structures et en fournissant des exemples de calcul. Son objectif est de simplifier l'application de normes complexes pour les professionnels du bâtiment tout en respectant les exigences de sécurité en cas de séisme.







![1. INTRODUCTION 3
1. INTRODUCTION
Le présent guide d’application vise les ossatures en éléments industrialisés
en béton à un seul niveau ou avec mezzanines. Il traite de la vérification
et du dimensionnement des bâtiments pour leur résistance aux séismes
conformément à :
−
− l’EN 1998-1 [
2
3
4
5
6
7
8
9
10
11
12
13
1
MS
] ;
−
− la norme NF DTU 23.3 [ 2
3
4
5
6
7
8
9
10
11
12
13
1
MS ].
Le guide se compose :
−
− d'une partie générale qui précise, pour le domaine d'application visé,
la méthodologie de vérification et de dimensionnement ;
−
−
d’exemples de calcul.
CSTB Editions pour SOCOTEC le 14/02/2017 15:28
IP de l'utilisateur: 64.208.250.81](https://image.slidesharecdn.com/pdfcoffee-211212051457/85/Pdfcoffee-com-eurocode-8-calcul-sismique-pdf-free-8-320.jpg)





![EFFETS DU SÉISME SUR LES STRUCTURES
EN ÉLÉMENTS INDUSTRIALISÉS EN BÉTON
10
−
−
2i
: coefficient de combinaison, pour la valeur quasi-permanente de
l’action variable Qk,i
;
−
−
: coefficient d’ajustement relatif à la concomitance des charges
variables et qui dépend de la catégorie du bâtiment ainsi que de la
localisation de la charge dans le bâtiment. Les valeurs de ce coefficient
sont données dans l’Annexe Nationale de l’EN 1998-1 [
2
3
4
5
6
7
8
9
10
11
12
13
1
MS ].
Dans le cas général, Il s’agit du poids propre supporté par les poteaux
augmenté de la moitié du poids propre des poteaux.
Remarque
Type d'action variable Étage
Catégories A à C* Toit
Étages à occupations corrélées
Étages à occupations indépendantes
1,0
0,8
0,5
Catégories D à F* et archives 1,0
* Catégories définies dans l'EN 1991-1-1 [
2
3
4
5
6
7
8
9
10
11
12
13
1
MS
].
Tableau 1 : Valeurs de pour le calcul de Ei
.
Dans le cas de chemins de roulement de ponts roulants, à défaut
d’indications contraires dans les documents particuliers du marché (DPM)
sur les taux de chargement et d’utilisation, il convient d’adopter :
−
−
pour la masse propre du pont roulant = 1 ;
−
−
pour la masse suspendue au pont roulant :
•
dans les directions horizontales = 0 ;
•
dans la direction verticale = 0,2.
Dans le cas général, Qk
est constitué par la charge pour entretien sur les
toitures, de la charge d’exploitation pour les ponts roulants.
Dans le cas des :
−
−
bâtiments à un niveau et diaphragme rigide en toiture, le calcul de mtot
est effectué sur l’ensemble de la toiture ;
−
−
bâtiments à un niveau, toitures souples, le calcul est effectué par
descente de charges pour chaque file de poteaux « i », dans les deux
directions horizontales (mtot,i
) ;
−
−
bâtiments avec mezzanine, le calcul est effectué pour l’ensemble
du niveau de la mezzanine (m1tot
) et l’ensemble du niveau de la toiture
(m2tot
).
CSTB Editions pour SOCOTEC le 14/02/2017 15:28
IP de l'utilisateur: 64.208.250.81](https://image.slidesharecdn.com/pdfcoffee-211212051457/85/Pdfcoffee-com-eurocode-8-calcul-sismique-pdf-free-14-320.jpg)
![3. MÉTHODOLOGIE DE DIMENSIONNEMENT 11
3.2.2 Rigidité latérale du bâtiment
■
■
Rigidité des poteaux
La raideur en flexion des sections est prise forfaitairement égale à :
−
−
2
I
=
cm
E
R
4
3 I
=
cm
E
R
3
2
3
L
E
K
cm
p
I
= 3
4
9
L
E
K
cm
p
I
=
)
(
)
1
(
3
8 3
m
N
r
G
K
ν
−
=
φ
pour les poteaux en béton armé (N/m) ;
−
−
2
I
=
cm
E
R
4
3 I
=
cm
E
R
3
2
3
L
E
K
cm
p
I
= 3
4
9
L
E
K
cm
p
I
=
)
(
)
1
(
3
8 3
m
N
r
G
K
ν
−
=
φ
pour les poteaux en béton précontraint (N/m) ;
soit une rigidité de poteau égale à
2
I
=
cm
E
R
4
3 I
=
cm
E
R
3
2
3
L
E
K
cm
p
I
= 3
4
9
L
E
K
cm
p
I
=
)
(
)
1
(
3
8 3
m
N
r
G
K
ν
−
=
φ
et
2
I
=
cm
E
R
4
3 I
=
cm
E
R
3
2
3
L
E
K
cm
p
I
= 3
4
9
L
E
K
cm
p
I
=
)
(
)
1
(
3
8 3
m
N
r
G
K
ν
−
=
φ
respectivement en béton armé et béton précontraint, avec :
−
− Ecm
, le module sécant de déformation du béton selon l’article 3.1.3
de l’EN 1998-1 ;
−
− I, le moment d’inertie de la section dans la direction sismique considérée ;
−
− L, la hauteur du poteau entre le point d’encastrement (à la sortie du fût
d’encuvement) et le point d’application de l’effort horizontal considéré.
■
■
Rigidité des fondations
En application de l’EN 1998-5 [
2
3
4
5
6
7
8
9
10
11
12
13
1
MS
] (paragraphe 6), la souplesse apportée
par les fondations devra être prise en compte lorsque le coefficient de
sensibilité aux déplacements relatifs , déterminé en négligeant la rigidité
de la fondation, sera supérieur à 0,2 (cf. calcul au paragraphe 1.13.4.2 de
l’EN 1998-5) ou en cas de sols mous (vitesse de propagation des ondes de
cisaillement inférieure à 100 m/s).
Les formules suivantes permettent d’accéder au calcul de la rigidité en
rotation d’une semelle de dimension a x b :
2
I
=
cm
E
R
4
3 I
=
cm
E
R
Kp
=
)
(
)
1
(
3
8 3
m
N
r
G
K
ν
−
=
φ
avec :
12
4
'
;
12
4
3
3 4
4
a
b
r
a
b
r
=
=
,
−
− R, r’ : rayon équivalent de la fondation, calculé par équivalence des
moments d’inertie avec une semelle cylindrique ;
−
− G : module de cisaillement du sol ;
−
−
v : coefficient de poisson du sol (v ≈ 0,3).
Le module de cisaillement du sol est donné par (paragraphe 3.2 (1) de
l'EN 1998-5) G = pvs
2
, avec :
−
−
p : masse volumique du sol ;
−
−
vs
: vitesse de propagation des ondes de cisaillement dans le sol, issue
de l’étude de sol.
CSTB Editions pour SOCOTEC le 14/02/2017 15:28
IP de l'utilisateur: 64.208.250.81](https://image.slidesharecdn.com/pdfcoffee-211212051457/85/Pdfcoffee-com-eurocode-8-calcul-sismique-pdf-free-15-320.jpg)





![3. MÉTHODOLOGIE DE DIMENSIONNEMENT 17
3.4 Calcul de l’action sismique
3.4.1 Détermination du coefficient de comportement de base
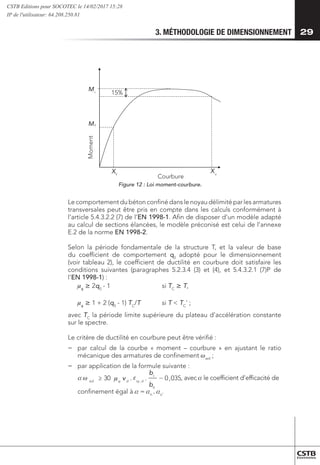
A défaut de justification particulière fondée sur un calcul de la ductilité
en déplacement (par exemple effectué à l’aide de l’annexe E de la norme
EN 1998-2 [
2
3
4
5
6
7
8
9
10
11
12
13
1
MS
]), les coefficients de comportement applicables q0
sont
décrits dans le tableau 5, en fonction du type de structure, pour la classe
de ductilité moyenne (DCM) au sens de l’EN 1998-1 et pour des bâtiments
réalisés à partir d’éléments d’ossature bénéficiant d’une certification NF ou
équivalente (cf. DTU 23.3), des pondérations sont prévues en fonction des
systèmes qualité mis en place selon les alinéas ci-dessous et le tableau 4.
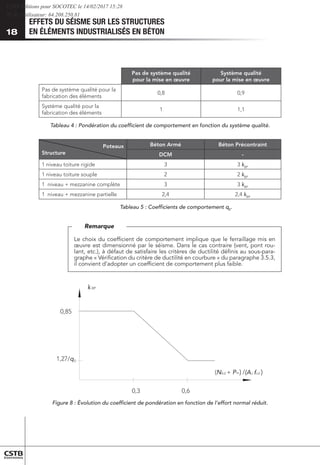
Pour les ossatures à poteaux en béton précontraint, un coefficient
de pondération KBp
est à appliquer en fonction du rapport (NEd
+ Pm,∞)/
(Ac
fcd
)) avec :
−
−
NEd
effort normal de calcul (utilisé dans la combinaison sismique) ;
−
−
Pm,∞
: précontrainte moyenne du poteau au temps infini. Ce coefficient
prend en compte le passage d’un amortissement réduit de 5 % à un
amortissement réduit de 2 % : il est donc applicable avec les spectres à
utiliser pour le béton armé.
Conformément à l’article 5.2.2.2 (10) de l’EN 1998-1, si un plan d’assurance
qualité est mis en place pour les étapes de conception du bâtiment, de
fabrication des éléments préfabriqués et mis en œuvre, le coefficient de
comportement q0
peut être majoré de 10 % (cf. DTU 23.3).
Lorsque les éléments d’ossature et leur mise en œuvre ne sont pas couverts
par un système qualité, les valeurs du coefficient de comportement q0
indiquées dans le tableau 5 sont à pondérer par un facteur 0,8.
Lorsque seule la mise en œuvre des éléments préfabriqués est couverte
par un système qualité, les valeurs du coefficient de comportement q0
indiquées dans le tableau 5 sont à pondérer par un facteur 0,9.
Lorsque les dispositions de l’article 5.11 de l’EN 1998-1 (ou de ce guide)
ne sont pas appliquées, la structure doit être vérifiée selon la classe de
ductilité basse (DCL) c’est-à-dire à l’aide de l’EN 1992-1-1 [
2
3
4
5
6
7
8
9
10
11
12
13
1
MS
] seul pour
déterminer et dimensionner le bâtiment pour sa résistance au séisme :
le coefficient de comportement q0
doit être pris égal à 1,5. A noter que
ce mode de conception est applicable uniquement aux zones de faible
sismicité.
Il est possible pour le cas visé d’effectuer des essais afin de prétendre à un
coefficient de comportement supérieur à 1,5.
Remarque
CSTB Editions pour SOCOTEC le 14/02/2017 15:28
IP de l'utilisateur: 64.208.250.81](https://image.slidesharecdn.com/pdfcoffee-211212051457/85/Pdfcoffee-com-eurocode-8-calcul-sismique-pdf-free-21-320.jpg)

![EFFETS DU SÉISME SUR LES STRUCTURES
EN ÉLÉMENTS INDUSTRIALISÉS EN BÉTON
20
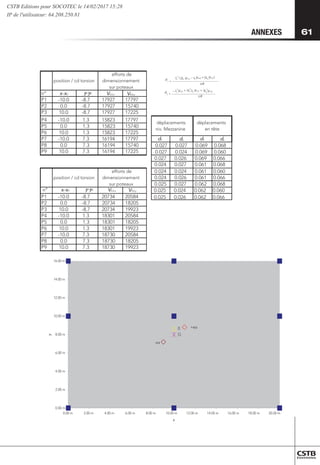
La figure suivante présente l’évolution du coefficient de comportement
maximal applicable pour satisfaire le critère 0,25, en fonction de la
hauteur L des poteaux. Le calcul est réalisé pour des poteaux en béton
armé de section carrée (souplesse des fondations négligées, rigidité des
poteaux déterminée sur la base d’une section pleine en C50/60, coefficient
de réduction pour prendre en compte la fissuration : 0,5) pour différentes
valeurs de l’effort normal réduit en tête de poteau n [n = Ptot
/ ( Ac
fck
/ c
)].
1.5
1.7
1.9
2.1
2.3
2.5
2.7
2.9
3.1
3.3
3.5
4.5 5.5 6.5 7.5 8.5 9.5 10.5 11.5
hauteur poteau h (m)
coefficient
de
comportement
max.
q
50 x 50 n = 3 %
50 x 50 n = 5 %
50 x 50 n = 7 %
50 x 50 n = 9 %
40 x 40 n = 5 %
60 x 60 n = 5 %
Figure 9 : Limitation du coefficient de comportement.
■
■
Bâtiments à un niveau, toitures souples
Le calcul se fait par file de poteaux dans les deux directions :
−
−
Ptot
= mtot,i
g ;
−
−
dr
= q mtot,i
Sd
(Ti
) / ktot,i
Se
(T) (Ti
/)2
;
−
−
h = L hauteur du poteau de la sortie de l’encuvement à la tête de
poteau.
En fixant une valeur limite de 0,3 pour , la condition précédente s’exprime
après simplification par :
g
m
L
k
q
tot
tot
3
,
0
≤
g
m
L
k
q
i
tot
i
tot
,
,
3
,
0
≤
.
.
Le graphique de la figure précédente permet de visualiser le coefficient de
comportement limite en fonction de l’équation précédente.
CSTB Editions pour SOCOTEC le 14/02/2017 15:28
IP de l'utilisateur: 64.208.250.81](https://image.slidesharecdn.com/pdfcoffee-211212051457/85/Pdfcoffee-com-eurocode-8-calcul-sismique-pdf-free-24-320.jpg)













![4. RÉFÉRENCES 37
4. RÉFÉRENCES
[
2
3
4
5
6
7
8
9
10
11
12
13
1
MS
] NF EN 1998-1 – « Eurocode 8 : Calcul des structures pour leur
résistance aux séismes - Partie 1 : règles générales, actions sismiques
et règles pour les bâtiments et son annexe nationale » – P06-030-1 –
AFNOR – Septembre 2005.
[ 2
3
4
5
6
7
8
9
10
11
12
13
1
MS ] NF DTU 23.3 – « Travaux de bâtiment - Ossatures en éléments
industrialisés en béton - Partie 1-1 : cahier des clauses techniques
types (CCT) - Partie 1-2 : critères généraux de choix des matériaux
(CGM) - Partie 2 : cahier des clauses administratives spéciales types -
Partie 3 : règles de calcul - Référence commerciale des parties P1-1,
P1-2, P2 et P3 du NF DTU 23.3 » – P19-202 – AFNOR – Juin 2008.
[
2
3
4
5
6
7
8
9
10
11
12
13
1
MS ] NF EN 1998-1/NA – « Eurocode 8 - Calcul des structures pour
leur résistance aux séismes - Partie 1 : règles générales, actions
sismiques et règles pour les bâtiments - Annexe nationale à la
NF EN 1998-1: 2005 - Règles générales, actions sismiques et règles
pour les bâtiments » – P06-030-1/NA – AFNOR – Décembre 2007.
[
2
3
4
5
6
7
8
9
10
11
12
13
1
MS
] NF EN 1991-1-1 – « Eurocode 1 - Actions sur les structures -
Partie 1-1 : actions générales - Poids volumiques, poids propres,
charges d'exploitation des bâtiments » – P06-111-1 – AFNOR –
Mars 2003.
NF P06-111-2/A1 – « Eurocode 1 : actions sur les structures -
Partie 1-1 : actions générales - Poids volumiques, poids propres,
charges d'exploitation des bâtiments - Annexe nationale à la
NF EN 1991-1-1 - Poids volumiques, poids propres, charges
d'exploitation des bâtiments » – P06-111-2/A1 – AFNOR – Mars 2009.
[
2
3
4
5
6
7
8
9
10
11
12
13
1
MS
] NF EN 1998-5 – « Eurocode 8 - Calcul des structures pour leur
résistance aux séismes - Partie 5 : fondations, ouvrages de
soutènement et aspects géotechniques » – P06-035-1 – AFNOR –
Septembre 2005.
NF EN 1998-5/NA – « Eurocode 8 - Calcul des structures pour
leur résistance aux séismes - Partie 5 : fondations, ouvrages de
soutènement et aspects géotechniques - Annexe nationale à la
NF EN 1998-5: 2005 - Fondations, ouvrages de soutènement et
aspects géotechniques » – P06-035-1/NA – AFNOR – Octobre 2007.
[
2
3
4
5
6
7
8
9
10
11
12
13
1
MS
] NF EN 1998-2 – « Eurocode 8 - Calcul des structures pour leur
résistance aux séismes - Partie 2 : ponts » – P06-032 – AFNOR –
Décembre 2006.
CSTB Editions pour SOCOTEC le 14/02/2017 15:28
IP de l'utilisateur: 64.208.250.81](https://image.slidesharecdn.com/pdfcoffee-211212051457/85/Pdfcoffee-com-eurocode-8-calcul-sismique-pdf-free-40-320.jpg)
![STRUCTURES EN BÉTON
SOUMISES À INCENDIE
38
NF EN 1998-2/NA – « Eurocode 8 - Calcul des structures pour leur
résistance aux séismes - Partie 2 : ponts - Annexe nationale à la
NF EN 1998-2: 2006 » – P06-032/NA – AFNOR – Octobre 2007.
[
2
3
4
5
6
7
8
9
10
11
12
13
1
MS
] NF EN 1992-1-1 – « Eurocode 2 - Calcul des structures en béton -
Partie 1-1 : règles générales et règles pour les bâtiments » –
P18-711-1 – AFNOR – Octobre 2005.
NF EN 1992-1-1/NA – « Eurocode 2 : calcul des structures en béton -
Partie 1-1 : règles générales et règles pour les bâtiments - Annexe
Nationale à la NF EN 1992-1-1: 2005 - Règles générales et règles
pour les bâtiments » – P18-711-1/NA – AFNOR – Mars 2007.
CSTB Editions pour SOCOTEC le 14/02/2017 15:28
IP de l'utilisateur: 64.208.250.81](https://image.slidesharecdn.com/pdfcoffee-211212051457/85/Pdfcoffee-com-eurocode-8-calcul-sismique-pdf-free-41-320.jpg)