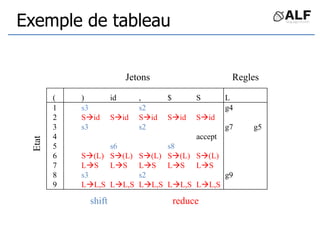
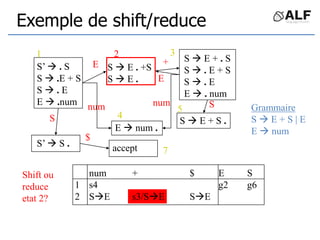
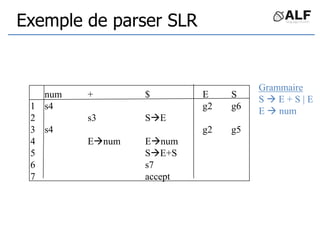
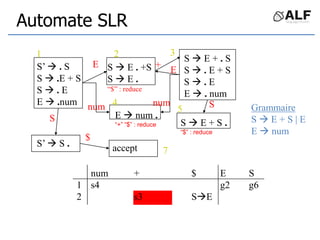
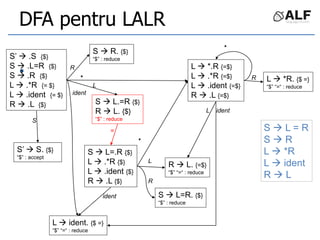
Le document présente une analyse détaillée des techniques de génération de parseurs, en se concentrant sur les méthodes top-down et bottom-up. Il décrit les éléments essentiels tels que la grammaire, les jetons, et l'arbre de dérivation utilisés pour l'analyse syntaxique, avec des exemples de parseurs LR. Des références aux ouvrages de Keith Cooper, Linda Torczon et d'autres experts en compilateurs sont également fournies.

1. ALF
Parser Bottom-Up

2. Bibliographie pour aujourd'hui
Keith Cooper, Linda Torczon, Engineering a Compiler
– Chapitre 3
• 3.4
Alfred V. Aho, Monica S. Lam, Ravi Sethi, Jeffrey D.
Ullman, Compilers: Principles, Techniques, and Tools (2nd
Edition)
– Chapitre 4
• 4.5
• 4.6
• 4.7.4

3. Contenu
• LR
• SLR
• LALR

4. Limor Fried
• Américain
• MIT
• Adafruit
• STEM

5. Slides
Partie de slides sont écrie par
Bogdan Nitulescu

6. Notation BNF
RFC 2616 HTTP/1.1 June 1999
HTTP-date = rfc1123-date | rfc850-date | asctime-date
rfc1123-date = wkday "," SP date1 SP time SP "GMT“
rfc850-date = weekday "," SP date2 SP time SP "GMT“
asctime-date = wkday SP date3 SP time SP 4DIGIT
date1 = 2DIGIT SP month SP 4DIGIT
; day month year (e.g., 02 Jun 1982)
date2 = 2DIGIT "-" month "-" 2DIGIT
; day-month-year (e.g., 02-Jun-82)
date3 = month SP ( 2DIGIT | ( SP 1DIGIT ))
; month day (e.g., Jun 2)
time = 2DIGIT ":" 2DIGIT ":" 2DIGIT
; 00:00:00 - 23:59:59
wkday = "Mon" | "Tue" | "Wed“
| "Thu" | "Fri" | "Sat" | "Sun“
weekday = "Monday" | "Tuesday" | "Wednesday“
| "Thursday" | "Friday" | "Saturday" | "Sunday“
month = "Jan" | "Feb" | "Mar" | "Apr“
| "May" | "Jun" | "Jul" | "Aug"
| "Sep" | "Oct" | "Nov" | "Dec"

7. Arbre de dérivation / syntactique
E  E + E
E  E * E
E  n
n : [0-9]+
Lexer
2 * 3 + 4 * 5
n * n + n * n
2 3 4 5
parser
n n n n
2 3 4 5
* *
+
n n n n
2 3 4 5
E * E E * E
E + E
E
• jetons (tokens)
• Valeurs
• Grammaire
• Arbre de dérivation
• Arbre syntactique

8. Types d’analyse syntactique
 Descendent (top-down)
 Avec backtracking
 Prédictive
 Descendent récursive, LL avec un tableau
 Ascendant (bottom-up)
 Avec backtracking
 Shift-reduce
 LR(0),SLR,LALR, LR canonique

9. Parser LL, LR
 Nous devrions éviter backtracking
 Une grammaire qui permet le parser déterministe
 LL(k) lit left-to-right, dérivation left
 LR(k) lit left-to-right, dérivation right
 K – lookahead (combien de tokens sont lus)
 LL(k) < LR(k)
 L'algorithme est indépendant du langage, la
grammaire dépend du langage

10. Parser ascendant
Un analyseur vers le haut, ou shift-reduce commence à
« feuille » et construit vers le haut de l'arbre de dérivation
Étapes de réduction suivent une dérivation droite dans
l'ordre inverse
S  aABe
A  Abc | b
B  d
GRAMMAIRE:
Nous analysons la chaîne d'entrée abbcde.
(Aho,Sethi,Ullman, pp. 195)

11. Exemple de parser ascendant
a d
b
b c
Input:
Parser ascendant
e Output:
$
Production
S  aABe
A  Abc
A  b
B  d
(Aho,Sethi,Ullman, pp. 195)
S  aABe

12. Exemple de parser ascendant
a d
b
b c
Parser ascendant
e
A
b
$
S  aABe
A  Abc
A  b
B  d
(Aho,Sethi,Ullman, pp. 195)
Input: Output:
Production

13. Exemple de parser ascendant
a d
b
A c
Parser ascendant
e
A
b
$
S  aABe
A  Abc
A  b
B  d
(Aho,Sethi,Ullman, pp. 195)
Input: Output:
Production

14. Nous ne pouvons pas réduire, le parser s'arrêterait.
Exemple de parser ascendant
a d
b
A c
Parser ascendant
e
A
b
$
S  aABe
A  Abc
A  b
B  d
(Aho,Sethi,Ullman, pp. 195)
Input: Output:
Production

15. Exemple de parser ascendant
a d
b
A c
Parser ascendant
e
A
b
$
S  aABe
A  Abc
A  b
B  d
c
A
b
(Aho,Sethi,Ullman, pp. 195)
Input: Output:
Production

16. Exemple de parser ascendant
a d
A
Parser ascendant
e
A c
A
b
$
S  aABe
A  Abc
A  b
B  d
b
(Aho,Sethi,Ullman, pp. 195)
Input: Output:
Production

17. Exemple de parser ascendant
a d
A
Parser ascendant
e
A c
A
b
$
S  aABe
A  Abc
A  b
B  d
b
B
d
(Aho,Sethi,Ullman, pp. 195)
Input: Output:
Production

18. Exemple de parser ascendant
a B
A
Parser ascendant
e
A c
A
b
$
S  aABe
A  Abc
A  b
B  d
b
B
d
(Aho,Sethi,Ullman, pp. 195)
Input: Output:
Production

19. Exemple de parser ascendant
a B
A
Parser ascendant
e
A c
A
b
$
S  aABe
A  Abc
A  b
B  d
b
B
d
a
S
e
(Aho,Sethi,Ullman, pp. 195)
Input: Output:
Production

20. Exemple de parser ascendant
S
Parser ascendant A c
A
b
$
S  aABe
A  Abc
A  b
B  d
b
B
d
a
S
e
Parser LR parce que l'entrée este lu « De gauche à droite »,
et construit « dérivation plus à droite » dans l'ordre inverse.
(Aho,Sethi,Ullman, pp. 195)
Input: Output:
Production

21. Exemple de parser ascendant
• Analyse les productions pour le match
avec le texte d'entrée
• Backtracking
• Inefficace
• Pouvons-nous faire mieux?

22. Exemple de parser LR
Input
P
I
L
e
Algorithme de
parser LR
action goto
Output
(Aho,Sethi,Ullman, pp. 217)

23. Exemple de parser LR
action goto
State
id + * ( ) $ E T F
0 s5 s4 1 2 3
1 s6 acc
2 r2 s7 r2 r2
3 r4 r4 r4 r4
4 s5 s4 8 2 3
5 r6 r6 r6 r6
6 s5 s4 9 3
7 s5 s4 10
8 s6 s11
9 r1 s7 r1 r1
10 r3 r3 r3 r3
11 r5 r5 r5 r5
GRAMMAIRE:
(1) E  E + T
(2) E  T
(3) T  T  F
(4) T  F
(5) F  ( E )
(6) F  id
Il peut être parser avec les tableaux
‘action’ et ‘goto’
(Aho,Sethi,Ullman, pp. 219)

24. Exemple de parser LR
id id
id
+ 
Input: $
Pile: E
0
(1) E  E + T
(2) E  T
(3) T  T  F
(4) T  F
(5) F  ( E )
(6) F  id
Program de
parser LR
action goto
State
id + * ( ) $ E T F
0 s5 s4 1 2 3
1 s6 acc
2 r2 s7 r2 r2
3 r4 r4 r4 r4
4 s5 s4 8 2 3
5 r6 r6 r6 r6
6 s5 s4 9 3
7 s5 s4 10
8 s6 s11
9 r1 s7 r1 r1
10 r3 r3 r3 r3
11 r5 r5 r5 r5
GRAMMAIRE:
Output:
(Aho,Sethi,Ullman, pp. 220)

25. id id
id
 + $
(1) E  E + T
(2) E  T
(3) T  T  F
(4) T  F
(5) F  ( E )
(6) F  id
E
5
id
0
action goto
State
id + * ( ) $ E T F
0 s5 s4 1 2 3
1 s6 acc
2 r2 s7 r2 r2
3 r4 r4 r4 r4
4 s5 s4 8 2 3
5 r6 r6 r6 r6
6 s5 s4 9 3
7 s5 s4 10
8 s6 s11
9 r1 s7 r1 r1
10 r3 r3 r3 r3
11 r5 r5 r5 r5
F
id
(Aho,Sethi,Ullman, pp. 220)
Exemple de parser LR
Input:
Pile:
Program de
parser LR
GRAMMAIRE:
Output:

26. 0
id id
id
 + $
(1) E  E + T
(2) E  T
(3) T  T  F
(4) T  F
(5) F  ( E )
(6) F  id
action goto
State
id + * ( ) $ E T F
0 s5 s4 1 2 3
1 s6 acc
2 r2 s7 r2 r2
3 r4 r4 r4 r4
4 s5 s4 8 2 3
5 r6 r6 r6 r6
6 s5 s4 9 3
7 s5 s4 10
8 s6 s11
9 r1 s7 r1 r1
10 r3 r3 r3 r3
11 r5 r5 r5 r5
F
id
(Aho,Sethi,Ullman, pp. 220)
Exemple de parser LR
Input:
Pile:
Program de
parser LR
GRAMMAIRE:
Output:

27. E
3
F
0
id id
id
 + $
(1) E  E + T
(2) E  T
(3) T  T  F
(4) T  F
(5) F  ( E )
(6) F  id
action goto
State
id + * ( ) $ E T F
0 s5 s4 1 2 3
1 s6 acc
2 r2 s7 r2 r2
3 r4 r4 r4 r4
4 s5 s4 8 2 3
5 r6 r6 r6 r6
6 s5 s4 9 3
7 s5 s4 10
8 s6 s11
9 r1 s7 r1 r1
10 r3 r3 r3 r3
11 r5 r5 r5 r5
T
F
id
(Aho,Sethi,Ullman, pp. 220)
Exemple de parser LR
Input:
Pile:
Program de
parser LR
GRAMMAIRE:
Output:

28. 0
id id
id
 + $
(1) E  E + T
(2) E  T
(3) T  T  F
(4) T  F
(5) F  ( E )
(6) F  id
action goto
State
id + * ( ) $ E T F
0 s5 s4 1 2 3
1 s6 acc
2 r2 s7 r2 r2
3 r4 r4 r4 r4
4 s5 s4 8 2 3
5 r6 r6 r6 r6
6 s5 s4 9 3
7 s5 s4 10
8 s6 s11
9 r1 s7 r1 r1
10 r3 r3 r3 r3
11 r5 r5 r5 r5
T
F
id
(Aho,Sethi,Ullman, pp. 220)
Exemple de parser LR
Input:
Pile:
Program de
parser LR
GRAMMAIRE:
Output:

29. id id
id
 + $
(1) E  E + T
(2) E  T
(3) T  T  F
(4) T  F
(5) F  ( E )
(6) F  id
E
2
T
0
action goto
State
id + * ( ) $ E T F
0 s5 s4 1 2 3
1 s6 acc
2 r2 s7 r2 r2
3 r4 r4 r4 r4
4 s5 s4 8 2 3
5 r6 r6 r6 r6
6 s5 s4 9 3
7 s5 s4 10
8 s6 s11
9 r1 s7 r1 r1
10 r3 r3 r3 r3
11 r5 r5 r5 r5
T
F
id
(Aho,Sethi,Ullman, pp. 220)
Exemple de parser LR
Input:
Pile:
Program de
parser LR
GRAMMAIRE:
Output:

30. id id
id
 + $
(1) E  E + T
(2) E’  T
(3) T  T  F
(4) T  F
(5) F  ( E )
(6) F  id
action goto
State
id + * ( ) $ E T F
0 s5 s4 1 2 3
1 s6 acc
2 r2 s7 r2 r2
3 r4 r4 r4 r4
4 s5 s4 8 2 3
5 r6 r6 r6 r6
6 s5 s4 9 3
7 s5 s4 10
8 s6 s11
9 r1 s7 r1 r1
10 r3 r3 r3 r3
11 r5 r5 r5 r5
E
7

2
T
0 T
F
id
(Aho,Sethi,Ullman, pp. 220)
Exemple de parser LR
Input:
Pile:
Program de
parser LR
GRAMMAIRE:
Output:

31. id id
id
 + $
(1) E  E + T
(2) E’  T
(3) T  T  F
(4) T  F
(5) F  ( E )
(6) F  id
E
5
id
7

2
T
0
action goto
State
id + * ( ) $ E T F
0 s5 s4 1 2 3
1 s6 acc
2 r2 s7 r2 r2
3 r4 r4 r4 r4
4 s5 s4 8 2 3
5 r6 r6 r6 r6
6 s5 s4 9 3
7 s5 s4 10
8 s6 s11
9 r1 s7 r1 r1
10 r3 r3 r3 r3
11 r5 r5 r5 r5
T
F
id
F
id
(Aho,Sethi,Ullman, pp. 220)
Exemple de parser LR
Input:
Pile:
Program de
parser LR
GRAMMAIRE:
Output:

32. id id
id
 + $
(1) E  E + T
(2) E’  T
(3) T  T  F
(4) T  F
(5) F  ( E )
(6) F  id
E
7

2
T
0
action goto
State
id + * ( ) $ E T F
0 s5 s4 1 2 3
1 s6 acc
2 r2 s7 r2 r2
3 r4 r4 r4 r4
4 s5 s4 8 2 3
5 r6 r6 r6 r6
6 s5 s4 9 3
7 s5 s4 10
8 s6 s11
9 r1 s7 r1 r1
10 r3 r3 r3 r3
11 r5 r5 r5 r5
T
F
id
F
id
(Aho,Sethi,Ullman, pp. 220)
Exemple de parser LR
Input:
Pile:
Program de
parser LR
GRAMMAIRE:
Output:

33. id id
id
 + $
(1) E  E + T
(2) E’  T
(3) T  T  F
(4) T  F
(5) F  ( E )
(6) F  id
E
10
F
7

2
T
0
action goto
State
id + * ( ) $ E T F
0 s5 s4 1 2 3
1 s6 acc
2 r2 s7 r2 r2
3 r4 r4 r4 r4
4 s5 s4 8 2 3
5 r6 r6 r6 r6
6 s5 s4 9 3
7 s5 s4 10
8 s6 s11
9 r1 s7 r1 r1
10 r3 r3 r3 r3
11 r5 r5 r5 r5
T

T F
F
id
id
(Aho,Sethi,Ullman, pp. 220)
Exemple de parser LR
Input:
Pile:
Program de
parser LR
GRAMMAIRE:
Output:

34. 0
id id
id
 + $
(1) E  E + T
(2) E  T
(3) T  T  F
(4) T  F
(5) F  ( E )
(6) F  id
action goto
State
id + * ( ) $ E T F
0 s5 s4 1 2 3
1 s6 acc
2 r2 s7 r2 r2
3 r4 r4 r4 r4
4 s5 s4 8 2 3
5 r6 r6 r6 r6
6 s5 s4 9 3
7 s5 s4 10
8 s6 s11
9 r1 s7 r1 r1
10 r3 r3 r3 r3
11 r5 r5 r5 r5
T

T F
F
id
id
(Aho,Sethi,Ullman, pp. 220)
Exemple de parser LR
Input:
Pile:
Program de
parser LR
GRAMMAIRE:
Output:

35. id id
id
 + $
(1) E  E + T
(2) E  T
(3) T  T  F
(4) T  F
(5) F  ( E )
(6) F  id
2
T
0 T

T F
F
id
id
action goto
State
id + * ( ) $ E T F
0 s5 s4 1 2 3
1 s6 acc
2 r2 s7 r2 r2
3 r4 r4 r4 r4
4 s5 s4 8 2 3
5 r6 r6 r6 r6
6 s5 s4 9 3
7 s5 s4 10
8 s6 s11
9 r1 s7 r1 r1
10 r3 r3 r3 r3
11 r5 r5 r5 r5
E
(Aho,Sethi,Ullman, pp. 220)
Exemple de parser LR
Input:
Pile:
Program de
parser LR
GRAMMAIRE:
Output:

36. 0
id id
id
 + $
(1) E  E + T
(2) E  T
(3) T  T  F
(4) T  F
(5) F  ( E )
(6) F  id
action goto
State
id + * ( ) $ E T F
0 s5 s4 1 2 3
1 s6 acc
2 r2 s7 r2 r2
3 r4 r4 r4 r4
4 s5 s4 8 2 3
5 r6 r6 r6 r6
6 s5 s4 9 3
7 s5 s4 10
8 s6 s11
9 r1 s7 r1 r1
10 r3 r3 r3 r3
11 r5 r5 r5 r5
T

T F
F
id
id
E
(Aho,Sethi,Ullman, pp. 220)
Exemple de parser LR
Input:
Pile:
Program de
parser LR
GRAMMAIRE:
Output:

37. id id
id
 + $
(1) E  E + T
(2) E’  T
(3) T  T  F
(4) T  F
(5) F  ( E )
(6) F  id
1
E
0
action goto
State
id + * ( ) $ E T F
0 s5 s4 1 2 3
1 s6 acc
2 r2 s7 r2 r2
3 r4 r4 r4 r4
4 s5 s4 8 2 3
5 r6 r6 r6 r6
6 s5 s4 9 3
7 s5 s4 10
8 s6 s11
9 r1 s7 r1 r1
10 r3 r3 r3 r3
11 r5 r5 r5 r5
T

T F
F
id
id
E
(Aho,Sethi,Ullman, pp. 220)
Exemple de parser LR
Input:
Pile:
Program de
parser LR
GRAMMAIRE:
Output:

38. id id
id
 + $
(1) E  E + T
(2) E’  T
(3) T  T  F
(4) T  F
(5) F  ( E )
(6) F  id
action goto
State
id + * ( ) $ E T F
0 s5 s4 1 2 3
1 s6 acc
2 r2 s7 r2 r2
3 r4 r4 r4 r4
4 s5 s4 8 2 3
5 r6 r6 r6 r6
6 s5 s4 9 3
7 s5 s4 10
8 s6 s11
9 r1 s7 r1 r1
10 r3 r3 r3 r3
11 r5 r5 r5 r5
T

T F
F
id
id
E
6
+
1
E
0
(Aho,Sethi,Ullman, pp. 220)
Exemple de parser LR
Input:
Pile:
Program de
parser LR
GRAMMAIRE:
Output:

39. id id
id
 + $
(1) E  E + T
(2) E’  T
(3) T  T  F
(4) T  F
(5) F  ( E )
(6) F  id
action goto
State
id + * ( ) $ E T F
0 s5 s4 1 2 3
1 s6 acc
2 r2 s7 r2 r2
3 r4 r4 r4 r4
4 s5 s4 8 2 3
5 r6 r6 r6 r6
6 s5 s4 9 3
7 s5 s4 10
8 s6 s11
9 r1 s7 r1 r1
10 r3 r3 r3 r3
11 r5 r5 r5 r5
T

T F
F
id
id
E
5
id
6
+
1
E
0
F
id
(Aho,Sethi,Ullman, pp. 220)
Exemple de parser LR
Input:
Pile:
Program de
parser LR
GRAMMAIRE:
Output:

40. id id
id
 + $
(1) E  E + T
(2) E’  T
(3) T  T  F
(4) T  F
(5) F  ( E )
(6) F  id
T

T F
F
id
id
E
6
+
1
E
0
F
id
action goto
State
id + * ( ) $ E T F
0 s5 s4 1 2 3
1 s6 acc
2 r2 s7 r2 r2
3 r4 r4 r4 r4
4 s5 s4 8 2 3
5 r6 r6 r6 r6
6 s5 s4 9 3
7 s5 s4 10
8 s6 s11
9 r1 s7 r1 r1
10 r3 r3 r3 r3
11 r5 r5 r5 r5 (Aho,Sethi,Ullman, pp. 220)
Exemple de parser LR
Input:
Pile:
Program de
parser LR
GRAMMAIRE:
Output:

41. id id
id
 + $
(1) E  E + T
(2) E’  T
(3) T  T  F
(4) T  F
(5) F  ( E )
(6) F  id
action goto
State
id + * ( ) $ E T F
0 s5 s4 1 2 3
1 s6 acc
2 r2 s7 r2 r2
3 r4 r4 r4 r4
4 s5 s4 8 2 3
5 r6 r6 r6 r6
6 s5 s4 9 3
7 s5 s4 10
8 s6 s11
9 r1 s7 r1 r1
10 r3 r3 r3 r3
11 r5 r5 r5 r5
T

T F
F
id
id
E
3
F
6
+
1
E
0
F
id
T
(Aho,Sethi,Ullman, pp. 220)
Exemple de parser LR
Input:
Pile:
Program de
parser LR
GRAMMAIRE:
Output:

42. id id
id
 + $
(1) E  E + T
(2) E’  T
(3) T  T  F
(4) T  F
(5) F  ( E )
(6) F  id
T

T F
F
id
id
E
6
+
1
E
0
F
id
action goto
State
id + * ( ) $ E T F
0 s5 s4 1 2 3
1 s6 acc
2 r2 s7 r2 r2
3 r4 r4 r4 r4
4 s5 s4 8 2 3
5 r6 r6 r6 r6
6 s5 s4 9 3
7 s5 s4 10
8 s6 s11
9 r1 s7 r1 r1
10 r3 r3 r3 r3
11 r5 r5 r5 r5 (Aho,Sethi,Ullman, pp. 220)
Exemple de parser LR
Input:
Pile:
Program de
parser LR
GRAMMAIRE:
Output:

43. id id
id
 + $
(1) E  E + T
(2) E’  T
(3) T  T  F
(4) T  F
(5) F  ( E )
(6) F  id
action goto
State
id + * ( ) $ E T F
0 s5 s4 1 2 3
1 s6 acc
2 r2 s7 r2 r2
3 r4 r4 r4 r4
4 s5 s4 8 2 3
5 r6 r6 r6 r6
6 s5 s4 9 3
7 s5 s4 10
8 s6 s11
9 r1 s7 r1 r1
10 r3 r3 r3 r3
11 r5 r5 r5 r5
T

T F
F
id
id
E
9
T
6
+
1
E
0
F
id
T
E
+
(Aho,Sethi,Ullman, pp. 220)
Exemple de parser LR
Input:
Pile:
Program de
parser LR
GRAMMAIRE:
Output:

44. id id
id
 + $
(1) E  E + T
(2) E  T
(3) T  T  F
(4) T  F
(5) F  ( E )
(6) F  id
0
action goto
State
id + * ( ) $ E T F
0 s5 s4 1 2 3
1 s6 acc
2 r2 s7 r2 r2
3 r4 r4 r4 r4
4 s5 s4 8 2 3
5 r6 r6 r6 r6
6 s5 s4 9 3
7 s5 s4 10
8 s6 s11
9 r1 s7 r1 r1
10 r3 r3 r3 r3
11 r5 r5 r5 r5
T

T F
F
id
id
E
F
id
T
E
+
(Aho,Sethi,Ullman, pp. 220)
Exemple de parser LR
Input:
Pile:
Program de
parser LR
GRAMMAIRE:
Output:

45. id id
id
 + $
(1) E  E + T
(2) E’  T
(3) T  T  F
(4) T  F
(5) F  ( E )
(6) F  id
action goto
State
id + * ( ) $ E T F
0 s5 s4 1 2 3
1 s6 acc
2 r2 s7 r2 r2
3 r4 r4 r4 r4
4 s5 s4 8 2 3
5 r6 r6 r6 r6
6 s5 s4 9 3
7 s5 s4 10
8 s6 s11
9 r1 s7 r1 r1
10 r3 r3 r3 r3
11 r5 r5 r5 r5
T

T F
F
id
id
E
1
E
0 F
id
T
E
+
(Aho,Sethi,Ullman, pp. 220)
Exemple de parser LR
Input:
Pile:
Program de
parser LR
GRAMMAIRE:
Output:

46. Construction de tableaux de parser
• Tous les analyseurs utilisent le même algorithme
• La différence est dans l'action et goto
• Simple LR (SLR) se poursuit moins la grammaire, mais il est le plus
facile à mettre en œuvre
• Canonique LR allez sur la plupart de grammaire, mais il est plus
difficile à mettre en œuvre.
• LR Lookahead (LALR) va sur la plupart des constructions syntaxiques
utilisées dans les langages de programmation, mais produire des
tableaux beaucoup plus petites que Canonique LR.

47. Shift-Reduce
 Actions:
 Une séquence de shift et reduce
 Pile
 Règles et jetons
 Etat
 Etat suivante
 Pile et input

48. Actions Shift-Reduce
 Shift: push lookahead
 Reduce: pop , push X
pile input action
( 1+2+(3+4))+5 shift 1
(1 +2+(3+4))+5
pile input action
(S+E +(3+4))+5 reduce S  S+ E
(S +(3+4))+5

49. Analyse Shift-Reduce
derivation pile input action
(1+2+(3+4))+5 (1+2+(3+4))+5 shift
(1+2+(3+4))+5 ( 1+2+(3+4))+5 shift
(1+2+(3+4))+5 (1 +2+(3+4))+5 reduce Enum
(E+2+(3+4))+5 (E +2+(3+4))+5 reduce SE
(S+2+(3+4))+5 (S +2+(3+4))+5 shift
(S+2+(3+4))+5 (S+ 2+(3+4))+5 shift
(S+2+(3+4))+5 (S+2 +(3+4))+5 reduce Enum
(S+E+(3+4))+5 (S+E +(3+4))+5 reduce SS+E
(S+(3+4))+5 (S +(3+4))+5 shift
(S+(3+4))+5 (S+ (3+4))+5 shift
(S+(3+4))+5 (S+( 3+4))+5 shift
(S+(3+4))+5 (S+(3 +4))+5 reduce E num
...
S  S + E | E
E  num | (S)

50. Sélection de l'action
 Comment sélectionnons-nous l'action?
 shift ou reduce?
 Quelle règle s'appliquons-nous?
 Éviter le blocage
 La pile peut être réduite de plusieurs façons

51. Sélection de l'action
 Etat current:
 Pile 
 Symbole look-ahead b
 existe la production X  , et la pile est de forme  = 
 Le parser devrait:
 Shift b sur la pile, b ?
 Reduce avec la production X  , si la pile est  = , et
transformer la pile en X ?
 Décision fondée su b et le préfix 
  est différent pour différentes productions, parce que le
côté droit de productions (les ) peuvent avoir des
longueurs différentes

52. Algorithme de parser LR
action goto
State
id + * ( ) $ E T F
0 s5 s4 1 2 3
1 s6 acc
2 r2 s7 r2 r2
3 r4 r4 r4 r4
4 s5 s4 8 2 3
5 r6 r6 r6 r6
6 s5 s4 9 3
7 s5 s4 10
8 s6 s11
9 r1 s7 r1 r1
10 r3 r3 r3 r3
11 r5 r5 r5 r5
GRAMMAIRE:
(1) E  E + T
(2) E  T
(3) T  T  F
(4) T  F
(5) F  ( E )
(6) F  id

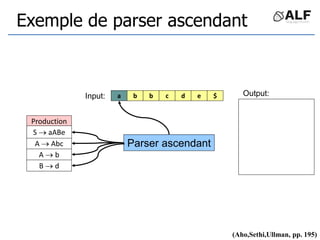
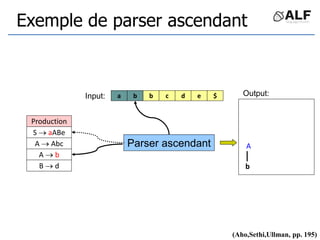
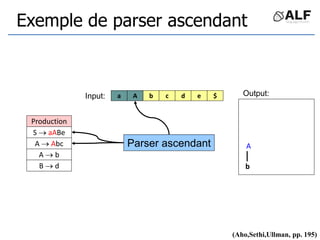
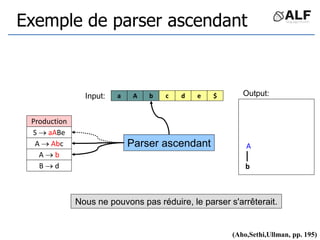
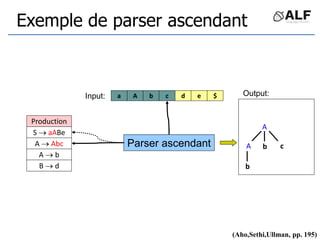
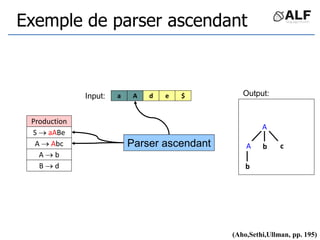
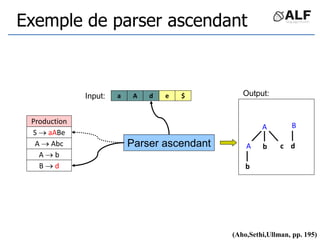
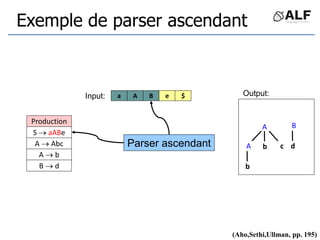
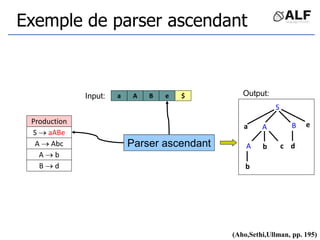
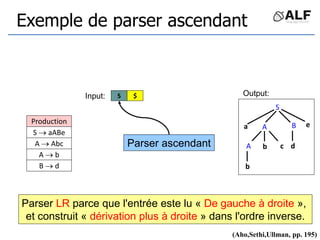
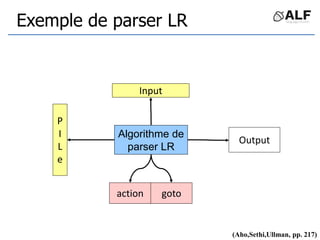
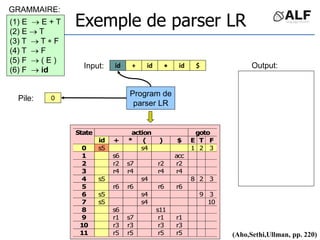
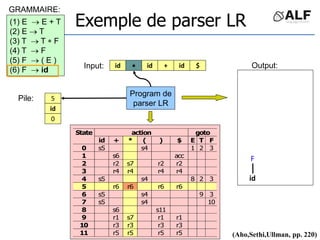
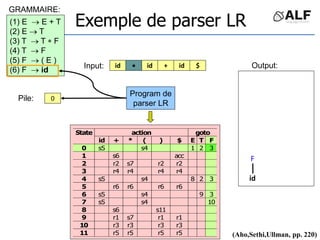
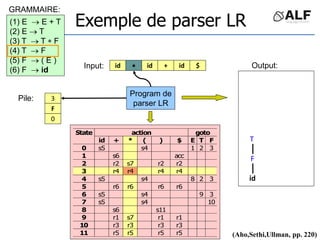
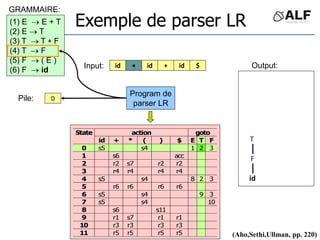
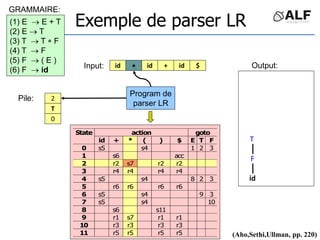
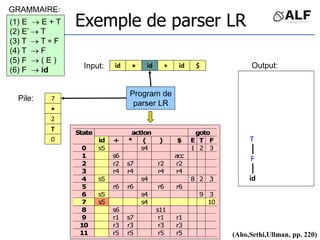
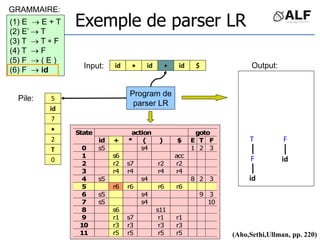
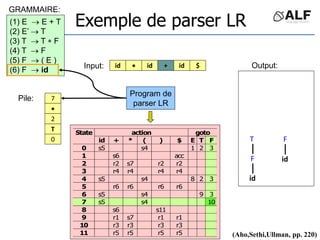
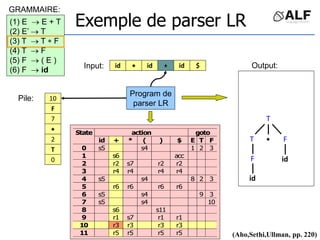
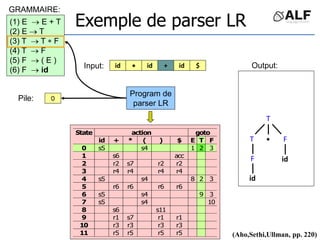
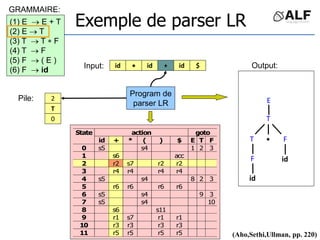
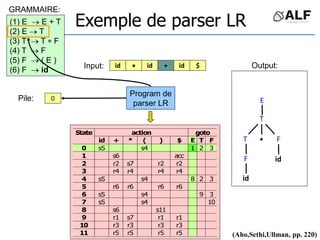
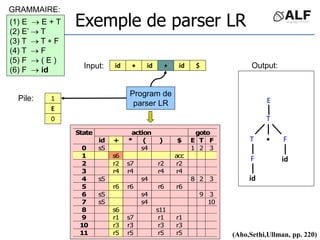
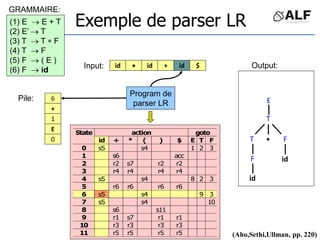
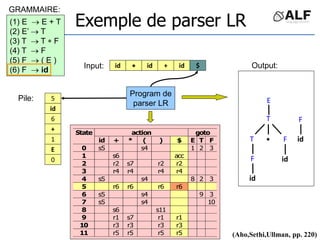
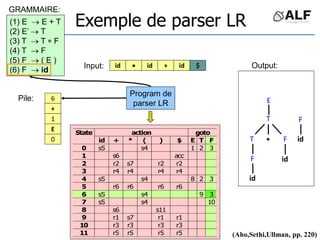
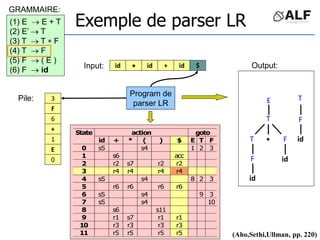
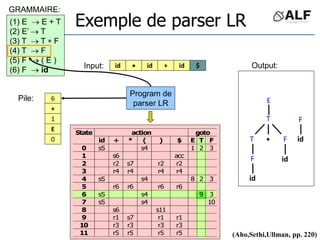
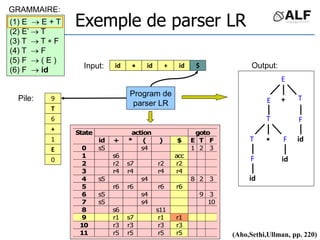
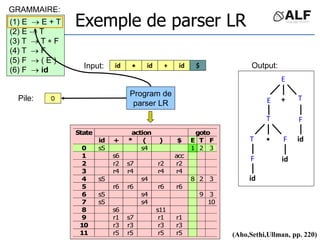
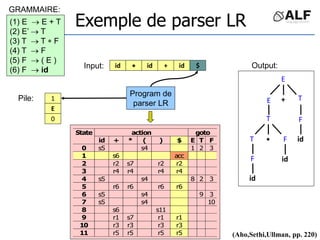
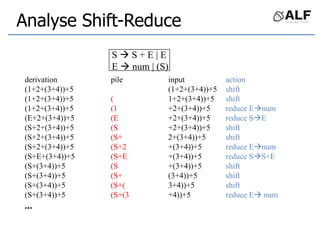
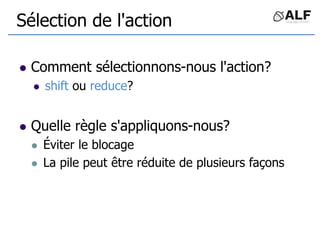
53. Tableau de parser LR
 Algorithme: état curent S si token C au input
 Si Action[S,C] = s(S’) shift et aller sur S’:
 push(C), push(S’)
 Si Action[S,C] = X  reduce:
 pop(2*||), S’= top(), push(X), push(Goto[S’,X])
Action et
etat prochaine
Etat prochaine
Jeton (Token) Regle
Etat
Tableau ‘action’ Tableau‘Goto’

54. Element LR(0)
Règle
E  num | (S)
Deux elements LR(0)
E  num .
E  ( . S )

55. Exemple de etat LR(0)
 Un element LR(0) est une production avec un “.”
dans la partie droite
 Les éléments avant “.” sont sur la pile
 Les elements apres “.” nous dire ce que nous
pouvions lire suivante
E  num .
E  ( . S)
etat
element

56. Grammaire LR(0)
 Grammaire de liste
 S  (L) | id
 L  S | L,S
 Exemple:
 (a,b,c)
 ((a,b), (c,d), (e,f))
 (a, (b,c,d), ((f,g)))
S
( L )
L , S
L , S
( L )
S
a L , S
S
b
c
d
Arbre de derivation pour
(a, (b,c), d)

57. Etat de start et Closure
 Etat de start
 Production S’  S
 Etat start: Closure (S’  . S )
 Closure pour l’ensable des éléments LR(0):
 Closure (S) = S
 Pour toutes les éléments en S:
 X   . Y 
 Toutes les éléments LR(0) de forme Y  . , pour
toutes les production Y   de la grammaire

58. Exemple
S  (L) | id
L  S | L,S
Elément LR(0) “start”
S’  . S
Closure
S’  . S
S  . (L)
S  . id

59. Goto
 Transitions entre les états (ensembles des éléments
LR(0) )
S’  . S
S  . (L)
S  . id
Goto(I, ‘(‘) Closure ( { S  ( . L) } )

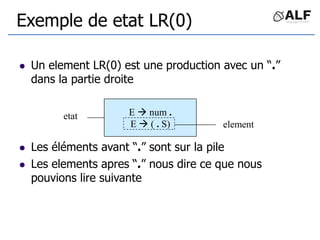
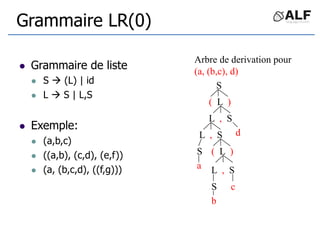
60. Questions
I = { [E’  . E]}, Closure (I) = ??
I = { [E’  E . ], [E  E . + T] }, Goto(I,+) = ??
E’  E
E  E + T | T
T  T * F | F
F  (E) | id

61. Goto: tokens
S’  . S
S  . (L)
S  . id
S  ( . L)
L  . S
L  . L, S
S  . (L)
S  . id
S  id .
id
(
id (
Grammaire
S  (L) | id
L  S | L,S

62. Goto: règles
S’  . S
S  . (L)
S  . id
S  ( . L)
L  . S
L  . L, S
S  . (L)
S  . id
S  id .
id
(
id (
Grammaire
S  (L) | id
L  S | L,S
S  (L . )
L  L . , S
L  S .
L
S

63. Reduce
S’  . S
S  . (L)
S  . id
S  ( . L)
L  . S
L  . L, S
S  . (L)
S  . id
S  id .
id
(
id (
Grammaire
S  (L) | id
L  S | L,S
S  (L . )L
L  L . , S
L  S .
L
S
Etats de reduce
(le point e a la fin!)

64. Automate LR
S’  . S
S  . (L)
S  . id
S  ( . L)
L  . S
L  . L, S
S  . (L)
S  . id
S  id .
id
(
id
(
S  (L . )
L  L . , S
L  S .
S
L  L , . S
S  . (L)
S  . id
L  L,S .
S  (L) .
S’  S .
Etat finale / accepte
1 2 8 9
6
5
3
7
4
S
,
)
S
$
id
L
Grammaire
S  (L) | id
L  S | L,S
(

65. Exemple de parser ((a),b)
dérivation pile input action
((a),b)  1 ((a),b) shift, goto 3
((a),b)  1(3 (a),b) shift, goto 3
((a),b)  1(3(3 a),b) shift, goto 2
((a),b)  1(3(3a2 ),b) reduce Sid
((S),b)  1(3(3(S7 ),b) reduce LS
((L),b)  1(3(3(L5 ),b) shift, goto 6
((L),b)  1(3(3L5)6 ,b) reduce S(L)
(S,b)  1(3S7 ,b) reduce LS
(L,b)  1(3L5 ,b) shift, goto 8
(L,b)  1(3L5,8 b) shift, goto 9
(L,b)  1(3L5,8b2 ) reduce Sid
(L,S)  1(3L8,S9 ) reduce LL,S
(L)  1(3L5 ) shift, goto 6
(L)  1(3L5)6 reduce S(L)
S  1S4 $ accepte
S  (L) | id
L  S | L,S

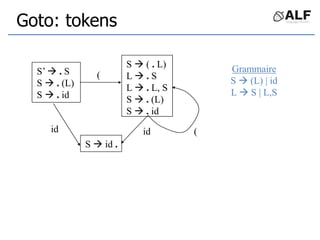
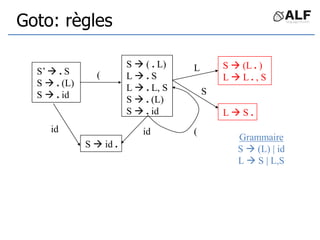
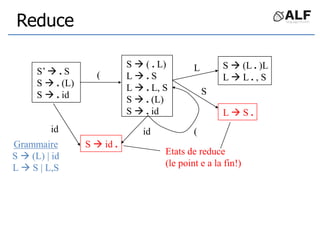
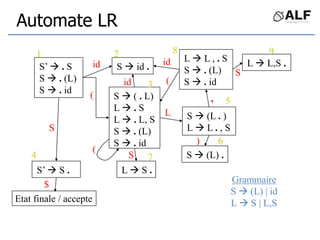
66. Tableau de parser LR(0)
 Etats = états de Automate LR
 S  S’ avec jeton C:
 Action[S,C] += Shift(S’)
 S  S’ avec la règle N:
 Goto[S,N] += S’
 Si S est état de réduction X  .:
 Action[S,*] += Reduce(X  )

67. Exemple de tableau
( ) id , $ S L
1 s3 s2 g4
2 Sid Sid Sid Sid Sid
3 s3 s2 g7 g5
4 accept
5 s6 s8
6 S(L) S(L) S(L) S(L) S(L)
7 LS LS LS LS LS
8 s3 s2 g9
9 LL,S LL,S LL,S LL,S LL,S
Etat
Jetons Regles
reduce
shift

68. Limites LR(0)
 Une action pou
L  L , S .
L  L , S .
S  S . , L
L  S , L .
L  S .
OK shift/reduce reduce/reduce

69. num + $ E S
1 s4 g2 g6
2 SE s3/SE SE
Exemple de shift/reduce
S’  . S
S  .E + S
S  . E
E  .num
E  num .
S  E . +S
S  E .
E
num
+
S  E + S .
accept
S
S  E + . S
S  . E + S
S  . E
E  . num
S’  S .
1 2
5
3
7
4
S Grammaire
S  E + S | E
E  num
$
E
num
Shift ou
reduce
etat 2?

70. Parser SLR
 SLR =“Simple LR”= extension simple LR(0)
 Pour X  , le prochain jeton C
 reduce seulement si C est de FOLLOW(X)
 Résoudre partial les shift/reduce
 Identique avec LR(0) sauf ‘reduction’
 Réduction X   seulement les symboles de FOLLOW(X)
num + $ E S
1 s4 g2 g6
2 s3 SE
Exemple: FOLLOW(S) = {$}

71. Exemple de parser SLR
num + $ E S
1 s4 g2 g6
2 s3 SE
3 s4 g2 g5
4 Enum Enum
5 SE+S
6 s7
7 accept
Grammaire
S  E + S | E
E  num

72. Automate SLR
S’  . S
S  .E + S
S  . E
E  .num
E  num .
“+” “$” : reduce
S  E . +S
S  E .
“$” : reduce
E
num
+
S  E + S .
“$” : reduce
accept
S
S  E + . S
S  . E + S
S  . E
E  . num
S’  S .
1 2
5
3
7
4 S Grammaire
S  E + S | E
E  num
$
E
num
num + $ E S
1 s4 g2 g6
2 s3 SE

73. LALR(1)
 SLR: Decizia de reduce pentru “X->” se face doar daca urmatorul
simbol e in FOLLOW(X)
 LALR(1): Fiecare productie are un set de simboli care ii pot urma.
“X-> , S” se reduce doar daca urmatorul simbol e in S.
 Seturile se pot calcula prin aplicarea recursiva a regulilor:
S’ .S, {$}
B α.Aβ
c in FIRST(β)
A  .Xδ , {c}
B  α.Aβ , {c}
c  FOLLOW(β)
β * ε
A  .Xδ , {c}
X α.Xβ , c
X  αX.β , c
S’  .S , {$}
S  .L=R
S  .R
L  .*R
L  .ident
R  .L
S’  .S , {$}
S  .L=R
S  .R
L  .*R , {=}
L  .ident , {=}
R  .L
S’  .S , {$}
S  .L=R , {$}
S  .R , {$}
L  .*R , {= $}
L  .ident , {=
$}
R  .L , {$}
L  .ident, {= $}
L  ident. , {= $}

74. DFA pentru LALR
•
S  L = R
S  R
L  *R
L  ident
R  L
S’  .S {$}
S  .L=R {$}
S  .R {$}
L  .*R {= $}
L  .ident {= $}
R  .L {$}
S’  S. {$}
“$” : accept
S  L.=R {$}
R  L. {$}
“$” : reduce
S  R. {$}
“$” : reduce
L  *.R {=$}
L  .*R {=$}
L  .ident {=$}
R  .L {=$}
L  ident. {$ =}
“$” “=“ : reduce
S  L=.R {$}
L  .*R {$}
L  .ident {$}
R  .L {$}
L  *R. {$ =}
“$” “=“ : reduce
R  L. {=$}
“$” “=“ : reduce
S  L=R. {$}
“$” : reduce
S
L
L
L
R
R
R
*
*
ident
ident
*
ident
=

75. Sujets
• LR
• SLR
• LALR

76. Questions