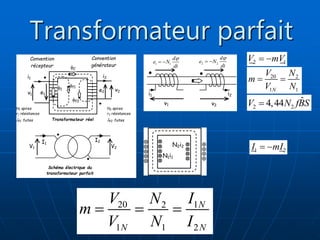
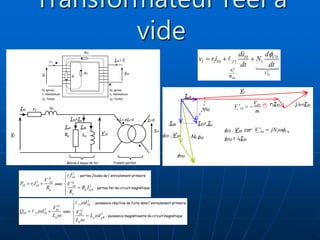
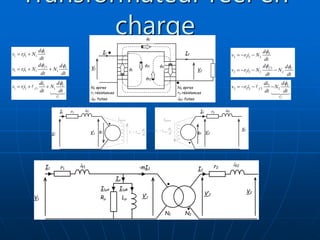
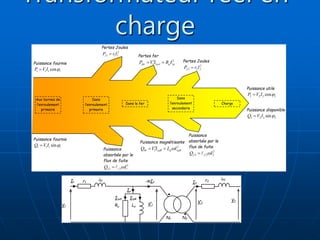
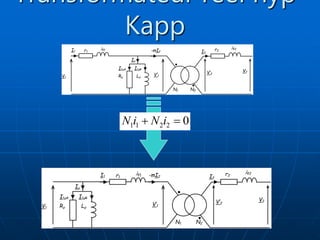
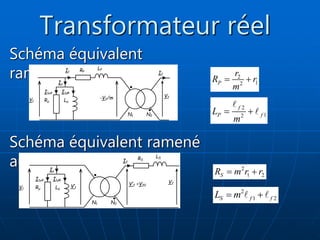
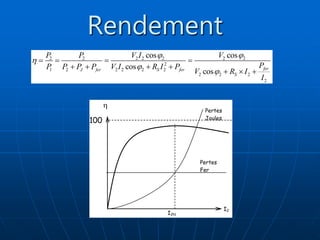
Le document traite des transformateurs monophasés, en expliquant les distinctions entre transformateurs parfaits et réels via des schémas électriques et des formulations mathématiques. Il explore les pertes, l'impédance, et la puissance dans les circuits, ainsi que les tests en continu. Les équations démontrent comment les variables interagissent à travers des charges et des enroulements.