Ce document présente les concepts de base de l'algorithmique et du fonctionnement des ordinateurs, incluant la définition d'un algorithme, les variables, les types de données, les instructions de base, et les structures de contrôle. Il aborde également les notions de portée des variables, les procédures, les fonctions, ainsi que les tableaux et les enregistrements. Enfin, il traite des algorithmes de tri, notamment le tri par sélection.

1. RÉSUMÉ ALGORITHME
POINTER@INFO
1 AFFECTATION, ENTRÉE ET SORTIE

2. Résolution de problème par ordinateur
Un Ordinateur : est une machine , Constitué des composants
électroniques capable de récupérer une donnée des périphérique
d’entrée, le stockage dans une mémoire, faire traitement grâce au
microprocesseur, pour fournir des résultats via les périphérique de sortie.
Problème
(à résoudre par
l’informatique)
Algorithme
Programme
(C)
Résultat
Analyse Traduction Exécution
Utilisateur Machine

3. Principe Entrée- Sortie- Traitement
Les Données
[Entrée]
Les Résultat
[Sortie]
Traitement
Périphérique
d’entrée:
- Clavier
- Micro
- Souris
- CD-ROM
- ….
Périphérique de
sortie:
- Ecran
- Imprimante.
- …
UC:
• Stockage:
- Mémoire centrale
RAM ou Autre.
• Traitement:
- Microprocesseur.
Restitution

4. Algorithme et structure Générale
• En informatique, un algorithme est une suite d’instructions
permettant d’arriver à un résultat donné.
• Un algorithme est écrit dans un langage humain (simple).

5. Notion d’un variable
Les données ainsi que les résultats des
calculs intermédiaires ou finaux, sont rangés
dans des cases-mémoires appelées
variables.
 Une variable:
 un emplacement mémoire nommé
 Prenant un nombre indéfini de valeurs
 différentes au cours du déroulement de
l'algorithme.
 .

6. Déclaration des variables
 La partie déclarations consiste à énumérer
toutes les variables dont on aura besoin au
cours de l'algorithme.
 Syntaxe :
Variable nom_de_la_variable : type
 Exemple :
variables nombre, k : entier
nom : chaine
a, b : booléen
 .

7. Type des variables et Constante
 Entier : les nombres entiers positifs ou négatifs (Simple, Long)
 Réel : les nombres réels (Simple, Double)
 Caractère : caractères alphabétiques et numériques
 Chaine : une chaine de caractère
 Booléen : les express ions logiques (Vrai, Faux)
Comme une variable, une constante est un emplacement
mémoire, mais dont la valeur stockée ne sera jamais modifiée au
cours du programme.
 Syntaxe :
Constante nom_de_la_constante = valeur
 Exemple :
Constante pi = 3.14

8. Les instructions
 Une instruction est une action que l'ordinateur est
capable d'exécuter
 Chaque langage de programmation fournit une
liste des instructions qu’on peut utiliser
 Les instructions de base sont:
 L’instruction d’affectation :
L’affectation permet d’affecter une valeur à une
variable.
Symbolisée en algorithmique par « ", elle précise le
sens de l’affectation.
Syntaxe : Variable  expression

9. Les opérateurs arithmétiques et relationnels
Opérateurs arithmétiques
+, -, *, /
Div ,Mod (Modulo)
Opérateurs relationnels =, <>, < , <= ,> ,>=
L’instruction de sortie:
L'instruction de sortie (d’écriture)
permet d’afficher des informations
a 'utilisateur à travers l'écran.
Syntaxe :
• Ecrire (expression)
Exemple:
• Ecrire("bonjour"):
• Ecrire ("la valeur de A : " , A)
L’instruction d’entrée:
L’instruction d’entrée ou de
lecture permet à l’utilisateur
de saisir des données au
clavier.
Syntaxe :
• Lire (variable)

10. RÉSUMÉ ALGORITHME
POINTER@INFO
2 LES TESTS OU STRUCTURES ALTERNATIVES
3 STRUCTURES ITÉRATIVES

11. La structure alternative:
Il est souvent nécessaire lorsque l'on écrit un programme de distinguer
plusieurs cas conditionnant l'exécution de certaines instructions
Utilisation d’une structure alternative : si on est dans tel cas, alors on fait
cela sinon on fait ceci.
Il n’y a que deux formes possibles pour un test
 Si (Condition)
Alors Instructions
Finsi
 Si (Condition) Alors
Instructions 1
Sinon
Instructions 2
Finsi
 Si la condition est vraie, se sont les
instructions1 qui seront exécutées
 Si la condition est fausse, se sont les
instructions2 qui seront exécutées
 La condition peut être une condition
simple ou une condition composée
de plusieurs conditions

12. Condition complexes et tables de vérité
C1 C2 C1 ET C2
VRAI VRAI VRAI
VRAI FAUX FAUX
FAUX VRAI FAUX
FAUX FAUX FAUX
C1 C2 C1 OU C2
VRAI VRAI VRAI
VRAI FAUX VRAI
FAUX VRAI VRAI
FAUX FAUX FAUX
C1 C2 C1 XOR C2
VRAI VRAI FAUX
VRAI FAUX VRAI
FAUX VRAI VRAI
FAUX FAUX FAUX
C1 NON C1
VRAI FAUX
FAUX VRAI
• Une condition composée est une condition
formée de plusieurs conditions simples reliées
par des opérateurs logiques: ET, OU, OU exclusif
(XOR) et NON
• L'évaluation d'une condition composée se fait
selon des règles présentées généralement dans
ce qu'on appelle tables de vérité

13. Tests impliqués
• Les tests peuvent avoir un degré quelconque d'imbrications
Si condition1 alors
instructions1
Sinon
Si condition2 alors
instructions2
Sinon
instructions3
Finsi
Finsi

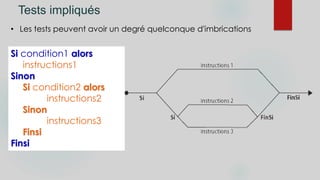
14. Selon … cas
• ‘Selon le cas’ permet de simplifier la syntaxe :
Syntaxe générale :
Selon < nom de variable >
Cas <Condition>: < instructions>
Cas <Condition>: < instructions>
…
[Sinon < instruction ou bloc >]
Fin Selon
Algorithme jour de la semaine
Variable n:entier
début
Lire (n)
Selon (n) :
Cas n = 1 : écrire ( ‘lundi’ )
Cas n = 2 : écrire ( ‘mardi’ )
Cas n = 3 : écrire ( ‘mercredi’ )
Cas n = 4 : écrire ( ‘jeudi’ )
Cas n = 5 : écrire ( ‘vendredi’ )
Cas n = 6 : écrire ( ‘samedi’ )
Cas n = 7 : écrire ( ‘dimanche’ )
sinon écrire ( ‘le numéro doit être
compris entre 1 et 7’ )
Fin Selon
Fin

15. La structure répétitive (boucle)
• On utilise la structure répétitive si on veut répéter des
mêmes actions (instructions) un certain nombre de
fois.
• Ces actions seront exécutées jusqu'à ce qu’une
condition soit remplie.
• La plupart des langages de programmation
proposent trois types de structure répétitive.

16. La structure répétitive (boucle) : POUR
POUR variable DE valeur initiale A valeur finale
FAIRE
instructions
FinPour
• Structure répétitive avec un compteur,
• Le traitement s'arrête lorsque en atteint la valeur finale,
Indice <=Val2 Actions
Faux
Vrai
Indice ← Val1
Indice ← Indice + 1

17. La structure répétitive (boucle) : TantQue
TantQue (condition) Faire
instructions
FTQ
• Ce qui signifie : tant que la condition est vraie, on exécute
les instructions
• la vérification de la condition s’effectue avant les actions.
Celles-ci peuvent donc ne jamais être exécutées
condition actions
Faux
Vrai

18. La structure répétitive (boucle) : TantQue
Faire
instructions
TantQue (condition)
Ce qui signifie : on exécute les instructions, tant que la
condition est vraie
Remarque : la vérification de la condition s’effectue
après les actions. Celles-ci sont donc exécutées au
moins une fois.
condition
actions
Faux
Vrai

19. La structure répétitive : REPETER...JUSQU’A...
REPETER
instructions
JUSQU’A (condition)
Remarque : la vérification de la condition s’effectue
après les actions. Celles-ci sont donc exécutées au
moins une fois.
condition
actions
Vrai
Faux

20. RÉSUMÉ ALGORITHME
POINTER@INFO
4 OPTIMISER L’ALGORITHME
(FONCTION ET PROCÉDURE)

21. La portée des variables. locales
Variables locales
Les variables déclarées dans une fonction ne sont accessibles que
dans cette Fonction.
Algorithme
/*déclarations de variables globales*/
Variables variable1, variable2 : TypeVariable
Début
type Fonction NomFonction ( TypeParam NomParam, TypeParam
NomParam, ...)
déclarations de variables locales
DEBUT
actions
FIN
Fin

22. La portée des variables. globales
Variables globales
- Les variables globales sont accessibles partout, sont placé au
début du programme
Algorithme
déclarations de variables globales
Début
Type Fonction NomFonction ( TypeParam NomParam, TypeParam
NomParam, ...)
/*déclarations de variables locales*/
Variables variable1, variable2 : TypeVariable
DEBUT
actions
FIN
Fin

23. La portée des variables. statiques
Variables statiques
• Les variables déclarées avec le mot clé « static » sont accessibles
uniquement dans le fichier où elles sont déclarées
• Une variable déclarée dans une fonction avec le mot-clé static
devant n’est pas supprimée à la fin de la fonction, elle conserve sa
valeur au fur et à mesure de l'exécution du programme
Algorithme
ENTIER STATIC Variables; /* ou bien*/
STATIC NomVariables: ENTIER;
Début
action
Fin

24. Les procédures
Définition et Déclaration d’une procédure:
Une Procédure est une suite d’instructions servant à réaliser une
tache précise en fonction d’un certain nombre de paramètres.
Déclaration
PROCEDURE NomProcedure ( TypeParam NomParam, TypeParam
NomParam, ...)
déclarations de variables locales
DEBUT
actions
FIN

25. Les procédures
Passage de paramètres par valeur:
 Pour que la valeur d’une variable du programme appelant ne soit
pas modifiée, il faut qu’en le passe par valeur.
 La procédure ou la fonction qui la manipule recevra cette valeur en
entrée du programme mais il s’agira de la copie en mémoire de la
valeur de la variable d’origine.
 Dans notre pseudo, le passage par valeur est indiqué par le mot clé
val.
TypeRetour FONCTION NomFonction ( val TypeParam NomParam …)
PROCEDURE NomProcedure ( val TypeParam NomParam …)

26. Les procédures
passage de paramètres par adresse
 Lorsque nous utilisons le passage d’une valeur par référence, nous
indiquons non sa valeur mais la référence en mémoire de celle-ci. Ainsi,
la procédure ou fonction manipule donc le même espace de mémoire.
 Toute modification apportée à la variable manipulée par la fonction ou
procédure touchera donc la variable d’origine.
 Dans notre algorithme , le passage par référence est indiqué par le mot
clé var.
TypeRetour FONCTION NomFonction ( var TypeParam NomParam …)
PROCEDURE NomProcedure ( var TypeParam NomParam …)

27. Les fonctions
Définition et déclaration:
 Une fonction est une procédure dont le but est de déterminer une
valeur et de la retourner au programme appelant.
 Une fonction ne retourne jamais un tableau.
 Déclaration:
TypeRetour FONCTION nomFonction ( type nom, type nom, …)
déclarations de variables locales
DEBUT
actions
RETOURNE valeur
FIN

28. Exploitation dans le programme principale
Appel procédure dans un programme principale:
 Pour appeler une procédure dans un programme principale en utilise cette
déclaration :
NomProcedure ( variable1, variable2 …) ;
 Pour chaque paramètre en affecte une valeur ou bien un nom de variable
connue dans le programme appelant cette procédure.
 Le nombre de paramètres dans l’appel d’une procédure doit correspondre au
nombre de paramètres de la procédure lors de sa définition.
 Le type du N ième paramètres dans l’appel d’une procédure doit correspondre
au type du N ième paramètre de la procédure lors de sa définition.

29. Exploitation dans le programme principale
Appel procédure dans un programme principale:
 Pour appeler une fonction dans un programme principale en utilise cette
déclaration :
variable  NomFonction ( variable1 , valeur2 , variable3 .... )
 Pour chaque paramètre en affecte une valeur ou bien un nom de variable
connue dans le programme appelant cette fonction.
 Le nombre de paramètres dans l’appel d’une fonction doit correspondre au
nombre de paramètres de la fonction lors de sa définition.
 Le type du N ième paramètres dans l’appel d’une fonction doit correspondre
au type du N ième paramètre de la fonction lors de sa définition.

30. RÉSUMÉ ALGORITHME
POINTER@INFO
5 LES TYPES COMPLEXES :
LES TABLEAUX ; LES CHAÎNES DE CARACTÈRES; LES
ENREGISTREMENTS ;LES TABLEAUX D’ENREGISTREMENTS.

31. Les Tableaux
• Regroupement de plusieurs variables de même type
sous un même nom.
• Un tableau permet de mémoriser plusieurs données
du même type.
• les tableaux permettent de stocker des données
nombreuses en mémoire centrale.
• Un tableau peut être un ensemble de valeurs
entières, réelles, booléennes, caractères …

32. les tableaux : une seule dimension
 Déclaration :
Tableau nom_du_tableau[Longueur] : Type
 Exemples :
Tableau mot[10] : Caractere
Tableau notes[25] : Entier
Tableau T[5] : Entier
T
Indices: 0 1 2 3 4
Le iéme élément de ce tableau sera adressé par T[i]
 T[2]  10 la 2ème case du tableau
T[4]  4 la 4ème case du tableau
10 4
Indices: 0 1 2 3 4
T
Ecrire(T[i]) : pour afficher
Lire(T[i]) : pour enregistrer

33. les tableaux : multidimensionnels
 Tableaux à deux dimensions : Généralement on utilise des
tableaux à une dimension, mais il existe également des
tableaux à deux dimensions.
 Exemple: Tableau T[3][5] : Caractere
10
Indices: 0 1 2 3 4
0
1
2
T T[1][3] = 10

34. les tableaux : Dynamiques
 Il arrive fréquemment que l’on ne connaisse pas à l’avance le nombre
d’éléments que devra comporter un tableau. Bien sûr, une solution
consisterait à déclarer un tableau avec une taille très grande. Cela
pourra avoir comme conséquence soit que cette taille ne nous nous
suffira pas ou qu’une place mémoire immense sera réservée sans être
utilisée.
 Afin de surmonter ce problème on utilise une instruction de re-
dimensionnement : Redim.
 Ecrire “Combien de notes à entrer?” ;
 Lire Nb ;
 Redim Notes(Nb-1) ;

35. Les chaines de caractères
 Une chaine de caractère est un tableau de caractères se
terminant par le caractère spécial ‘0’ (qui a 0 pour code
ASCII).
 Le caractère ‘0’ sert à repérer la fin de la chaine. On peut
ainsi passer une chaine de caractères en paramètre à une
fonction, sans avoir besoin de passer un deuxième paramètre
contenant le nombre de caractères.
Déclaration : variables nomDeLaVariable: Chaine;
‘e’ ‘x’ ‘e’ ‘’
‘m’ ‘p’ ‘l’ ‘e’ ‘0’

36. Enregistrement
 Définition :
 Les enregistrements dite aussi des variable composée, structure. C’est
un ensemble d’information de types différents.
 Une seul information est un champ nommé par un nom et un type.
ExempleEnregistrement :
Type
Etudiant = Enregistrement
Code: entier
Nom : chaine
Prénom : chaine
Adresse : chaine
Email : chaine.
Fin Enregistrement
Déclaration:
Type
<Nom de Type> = Enregistrement
<Nom de champ 1> : <Type data>
<Nom de champ 2> : <Type data >
……
Fin Enregistrement

37. Exemple Enregistrement
 Enregistrement :
Type
Etudiant = Enregistrement
Code: entier
Nom : chaine
Prénom : chaine
Adresse : chaine
Email : chaine.
Fin Enregistrement
//…………………………
Ecrire(« code Etudiant »)
Ecrire(« Code: » A.Code)
Ecrire(« Nom : » A.Nom)
Ecrire(« Prenom : »
A.Prenom)
Ecrire(« Adress: »
A.Adresse)
Ecrire(« Tel: » A.Email)
Fin
Variable A,B,C : Abonne
Début
Lire(A)
Ecrire(« code Etudiant »)
Lire (A.Code)
Ecrire(« nom Etudiant »)
Lire (A.Nom)
Ecrire(« prénom Etudiant »)
Lire (A.Prenom)
Ecrire(« Adresse Etudiant »)
Lire (A.Adresse)
Ecrire(« Email Etudiant »)
Lire (A.Email)

38. Les tableaux d’enregistrements
Type
<Nom de Type> = Enregistrement
<Nom de champ 1> : <Type de données>
<Nom de champ 2> : <Type de données> ……
Fin Enregistrement
Algorithme nom_algorithme
Variable:
Tableau nom_tableau[ ] : nom_de_type
Début ….

39. RÉSUMÉ ALGORITHME
POINTER@INFO
6 LES ALGORITHMES DE TRI :
• Le tri par sélection.
• Le tri par insertion
• Le tri à bulles
• Tri par comptage

40. Les algorithmes de tri: Le tri par sélection
 Tris élémentaires : Le tri par sélection
Le principe:
 On cherche l’élément de plus petite valeur
pour l’échanger avec l’élément en première
position.
 Puis on cherche l’élément ayant la deuxième
plus petite valeur pour l’échanger avec
l’élément en deuxième position, et ainsi de
suite
 Il faut
 1 boucle pour parcourir le tableau et
sélectionner tous les éléments;
 1 boucle pour recherche le minimum parmi
les éléments non triés.
Exemple:

41. Tris élémentaires : Le tri par sélection
Exemple : Simuler l’algorithme du tri par sélection sur le tableau suivant on
montrant les étapes d’exécution 9 4 1 7 3
Principe : à l'étape i, on sélectionne le plus petit élément parmi les
(n - i +1) éléments du tableau les plus à droite. On l'échange ensuite avec
l'élément i du tableau
Étape 1: on cherche le plus petit parmi les 5 éléments du tableau. On
l’identifie en troisième position, et on l’échange alors avec l’élément 1 :
Étape 2: on cherche le plus petit élément, mais cette fois à partir du
deuxième élément. On le trouve en dernière position, on l'échange
avec le deuxième:
Étape 3:
1 4 9 7 3
1 3 9 7 4
1 3 4 7 9

42.  Tris élémentaires : Le tri par sélection
Algorithme: Supposons que le tableau est noté T et sa taille N
Pour i de 0 A N-2 Faire
indice  i
Pour j de i+1 A N-1 Faire
Si (T[j] < T[indice]) Alors
indice  j Recherche de l’élément concerné
Finsi
FinPour
temp  T[indice]
T[indice]  T[i] Permutation des deux valeurs
T[i]  temp
FinPour

43.  Tris élémentaires : Le tri par insertion
 Le principe:
 On Considère les éléments les uns après les
autres en insérant chacun à sa place parmi
les éléments déjà triés.
 Il faut:
 1 boucle pour parcourir le tableau et
sélectionner l’élément à insérer;
 1 boucle pour décaler les éléments plus
grands que l’élément à insérer;
 Insérer l’élément.
Exemple:

44.  Tris élémentaires : Le tri par insertion
Algorithme: Supposons que le tableau est noté T et sa taille N
Pour i de 1 A N-1 Faire
mem T[i]
j  i
TantQue ( j > 0 et T[j-1] > mem )
T[j]  T[j-1]
j  j-1
FTQ
T[j]  mem
FinPour
2 56 4 7 0
Exemple:
- Prendre l’élément i
- Insérer i dans l’ordre entre 0 et i
- Continuer à partir de i+1
2, 56, 4, 7, 0
2, 56, 4, 7, 0
2, 56, 4, 7, 0
2, 4, 56, 7, 0
2, 4, 7, 56, 0
0, 2, 4, 7, 56

45. Tris élémentaires : Le tri à bulles
 Le principe:
 On parcours autant de fois le tableau en permutant 2 éléments adjacents
mal classés qu’il le faut pour que le tableau soit trié.
 Il faut 1 boucle pour parcourir tout le tableau et sélectionner les
éléments un à un
 Il faut 1 boucle pour permuter les éléments adjacents.

46.  Tris élémentaires : Le tri à bulles
Algorithme: Supposons que le tableau est noté T et sa taille N
Permut  1
TantQue (Permut = 1)
Permut  0
Pour i De 0 A N-2 Faire
Si (T[i] > T[i+1]) Alors
temp  T[i]
T[i]  T[i+1]
T[i+1]  temp
Permut  1
FinSi
FinPour
FTQ
Permut  Vrai
TantQue (Permut)
Permut  Faux
Pour i De 0 A N-2 Faire
Si (T[i] > T[i+1]) Alors
temp  T[i]
T[i]  T[i+1]
T[i+1]  temp
Permut  Vrai
FinSi
FinPour
FTQ

47.  Tris élémentaires : Tri par comptage
 Le tri par comptage consiste pour chaque élément du tableau a
compter combien d‘éléments sont plus petits que lui, grâce a ce
chiffre on connait sa position dans le tableau résultat.
Liste initiale : 52 10 1 25 62 3 8 55 3 23
Poids du mot 7 4 0 6 9 1 3 8 1 5
Position 8 5 1 7 10 2 4 9 3 6
Tri 1 3 3 8 10 23 25 52 55 62
Exercice
Ecrire l’algorithme de Tri par comptage Pour réaliser ce tri, utilisez
plusieurs tableaux
(Prenez garde aux valeurs identiques !)

48. Solution
//Remplissage du tableau Poids par les
positions
Pour i de 0 a N-1 Faire
Poids[i]  0
Pour j de 0 a N-1 Faire
Si (T[j] < T[i]) alors
Poids[i]  Poids[i] + 1
Fin si
Fin pour
Fin pour
//Elimination des positions doubles du tableau
Poids
Pour i de 0 a N-1 Faire
Pour j de 0 a N-1 Faire
Si ((Poids[i] = Poids[j]) et (i <> j)) alors
Poids[j]  Poids[j] + 1
Fin si
Fin pour
Fin pour
//Tri des éléments dans le tableau temporaire X
Pour i de 0 a N-1 Faire
X[ Poids[i] ]  T[i]
Fin pour
//Copie des éléments triés dans T
Pour i de 0 a N-1 Faire
T[i]  X[i]
Fin pour

49. RÉSUMÉ ALGORITHME
POINTER@INFO
7 LES ALGORITHMES DE TRI :
• Le tri rapide
• Le recherche séquentielle
• Recherche dichotomique*

50. Les algorithmes de tri:
Tris avancés: Tri rapide
Le tri rapide est un tri récursif basé sur l'approche "diviser pour régner"
(consiste à décomposer un problème d'une taille donnée à des sous
problèmes similaires mais de taille inférieure faciles à résoudre)
Description du tri rapide :
1) on considère un élément du tableau qu'on appelle pivot
2) on partitionne le tableau en 2 sous tableaux : les éléments inférieurs ou
égaux à pivot et les éléments supérieurs à pivot. on peut placer ainsi la
valeur du pivot à sa place définitive entre les deux sous tableaux
3) on répète récursivement ce partitionnement sur chacun des sous
tableaux crées jusqu'à ce qu'ils soient réduits à un à un seul élément

51. Tris avancés: Tri rapide
Le principe diviser pour résoudre
1- Choisir un seul (pivot)
2- mettre les éléments plus petit que
le seuil à gauche du seuil et les
éléments plus grands à droite
3- recommencer séparément sur les
parties droite et gauche
 Il faut partitionner selon un pivot.
 Recommencer sur les partitions
(récursion)

52.  Tris avancés: Tri rapide
Procédure Tri rapide
Procédure TriRapide(tableau T : réel par adresse, p,r: entier par valeur)
variable q: entier
Si p <r alors
Partition(T,p,r,q)
TriRapide(T,p,q-1)
TriRapide(T,q+1,r)
FinSi
Fin
A chaque étape de récursivité on partitionne un tableau T[p..r] en
deux sous tableaux T[p..q-1] et T[q+1..r] tel que chaque élément de
T[p..q-1] soit inférieur ou égal à chaque élément de A[q+1..r] . L'indice
q est calculé pendant la procédure de partitionnement.

53.  Tris avancés: Tri rapide
Procédure de partition
Procédure Partition(tableau T : réel par adresse, p,r: entier par valeur,
q: entier par adresse )
Variables i, j: entier pivot: réel
pivot← T[p], i←p+1, j ← r
TantQue (i<=j)
TantQue (i<=r et T[i] <=pivot) i ← i+1 FTQ
TantQue (j>=p et T[j] >pivot ) j ← j-1 FTQ
Si (i <j) alors
Echanger(T[i], T[j]), i ← i+1, j ← j-1
FinSi FTQ
Echanger(T[j], T[p]) q ← j
Fin

54. Les algorithmes de recherche rapide :
Algorithmes de Recherche séquentielle
Le principe de l'algorithme de recherche séquentielle consiste à parcourir un
tableau d'éléments dans l'ordre de ses indices jusqu'à ce qu'un élément
recherché soit trouvé ou bien que la fin du tableau soit atteinte et le rang
(indice) de l'élément est alors retourné.
Description : Algorithmes de Recherche séquentielle
L'algorithme ci-dessus est une fonction qui prend en entrée, un tableau T
d'entiers non triés de N éléments et un entier ValRech qui est la valeur
recherché.
La boucle Pour consiste à parcourir le tableau en comparant la valeur
recherchée avec chaque élément du tableau. Si la valeur est trouvée,
l'instruction Retourner i interrompt la fonction. Dans ce cas la fonction
renvoie la valeur de i, c'est à dire l'indice de l'élément recherché. Lorsque la
valeur recherchée n'est pas trouvée dans le tableau, la fonction renvoie -1.

55. Les algorithmes de recherche rapide :
 Cas : premier élément trouvé
entier Fonction RechSéq(T : Tableau
d'entiers, N : entier, ValRech
: entier)
Variable i : entier
Début
Pour (i de 0 à N-1) Faire
Si (T[i] = ValRech) Alors
Retourner i
FinSi
FinPour
Retourner -1
Fin
 Cas 2: dernier élément trouvé
entier Fonction RechSéq(T : Tableau
d'entiers, N : entier, ValRech : entier)
Variable i , p: entier
Début
p <- -1
Pour (i de 0 à N-1) Faire
Si (T[i] = ValRech) Alors
p <- i
FinSi
FinPour
Retourner p
Fin

56. Les algorithmes de recherche rapide :
Algorithmes de Recherche dichotomique
L'algorithme de recherche dichotomique est un algorithme
efficace et rapide pour la recherche d'un élément dans un
tableau Trié. Le principe de cet algorithme consiste à
diviser le tableau en deux parties et à comparer la valeur
recherchée avec l'élément situé au milieu du tableau
(l'élément médian).
Si la valeur recherchée correspond à l'élément médian,
alors l'algorithme s'arrête et renvoie l'indice de cet élément.
Sinon l'algorithme va répéter la recherche uniquement
dans la partie qui peut contenir la valeur recherchée.

57. entier Fonction RechDich(
T: tableau d'entiers, N : entier,
ValRech : entier)
Variables D, F, M : entier
D ← 1
F ← N
Début
TantQue (D <= F) Faire
M ← (D + F) / 2)
Si (T[M] = ValRech) Alors
Retourner M
Sinon
Si (T[M] < ValRech) Alors
D ← M + 1
Si (T[D] = ValRech) Alors
Retourner D
FinSi
Sinon
F ← M - 1
Si (T[F] =
ValRech) Alors
Retourner F
FinSi
FinSi
FinSi
FTQ
Retourner -1
Fin

58. Les algorithmes de recherche rapide :
Description de Algorithmes de Recherche dichotomique
L'algorithme ci-dessus est une fonction qui prend en entrée,
un tableau T d'entiers trié, la taille de ce tableau N et un
entier ValRech qui est la valeur recherchée.
Les variables D et F correspondent aux indices
respectivement début et fin de l'intervalle de recherche
dans le tableau. M c'est l'indice médian de l'intervalle de
recherche.
Le tableau ci-dessous montre le fonctionnement de cet
algorithme. La valeur recherchée est 35.

59. RÉSUMÉ ALGORITHME
POINTER@INFO
8 LES FICHIERS:

60. Ouverture
 Lors de l’ouverture du fichier il faut préciser pour quelle
opération celui-ci sera utilisé, Entrée, Sortie ou Ajout. On
indiquera aussi par un n° le buffer qui sera la
représentation du fichier en mémoire:
 OUVRIR nomdufichier POUR operation COMME NumBuffer
60
Nomdufichier : nom physique complet du fichier, exemple
c:monfichier.txt
Operation : ENTREE, SORTIE ou AJOUT (INPUT, OUTPUT ou APPEND)
NumBuffer : un numéro de 1 à 255 précédé du caractère #

61. Tester sur l’existence du fichier
 lors d’une ouverture pour lecture ou ajout, il faut
s’assurer de l’existence préalable du fichier.
 la fonction qui nous permet d’obtenir la certitude de
l’existence ou non d’un fichier à un emplacement
donné sur le disque est une fonction booléenne qui
renverra vrai si le fichier existe ou faux sinon.
61

62. Tester sur l’existence du fichier
SI (EXISTEFIC ‘c:liste.txt’ = VRAI) ALORS
OUVRIR ‘c:liste.txt’ POUR LECTURE COMME #1
SINON
ECRIRE ‘Le fichier demandé n’’existe pas’
FINSI
62

63. Opérations sur les données
 Deux opérations très simples : la lecture depuis le buffer et
l’écriture dans le buffer :
 MaVariable  LIREFIC NumBuffer
 ECRIREFIC MaVariable NumBuffer
63

64. Détection de fin de fichier
 Une variable système permet de définir que le programme a
atteint la fin du fichier et qu’il n’y a plus d’éléments à lire.
 Cette variable sera nommée par un mot clé réservé EOF pour
End Of File assignée par buffer.
 EOF NumBuffer
64

65. Exemple
OUVRIR "c:liste.txt’’ POUR LECTURE COMME #1
TANT QUE (NON (EOF #1)) FAIRE
VARTAMP  LIREFIC #1
ECRIRE (VARTAMP)
FTQ
65

66. Fermeture
 Pour terminer le traitement d’un fichier, il faudra libérer celui-ci
pour qu’il puisse être de nouveau utiliser par un autre
programme.
 Attention, l’opération de fermeture provoque le transfert des
données de la zone tampon, buffer, sur le disque dans le cas
d’un fichier ouvert pour sortie ou ajout. Si vous oubliez de fermer
le fichier, les données de celui-ci ne seront pas sauvegardées.
 FERMERFIC NumBuffer
66