coursalgorithmique9-10.ppt

Algorithmique
Mme Khadija BOUZAACHANE
Année universitaire : 2009-2010

Introduction
 Avez vous déjà déchiffré un mode d’emploi
pour faire fonctionner un DVD, ou bien la
télévision ou un répondeur téléphonique? Si
oui, sans le savoir, vous avez déjà exécuté
des algorithmes.
 Avez-vous déjà indiqué un chemin à un
touriste égaré ?
 Un algorithme, c’est une suite d’instructions,
qui une fois exécutée correctement, conduit à
un résultat donné. Si l’algorithme est juste, le
résultat est le résultat voulu, et le touriste se
retrouve là où il voulait aller
24/02/2023 3

Introduction
 Qu’est-ce qu’un algorithme?
◦ Est une suite d’instructions écrite en langage
d’algorithme qui résout un problème et qui peuvent
être programmé par n’importe quel langage.
 Une suite d'instructions serait :
1. Se lever
2. Prendre sa douche
3. Prendre le petit déjeuner
4. S'habiller
24/02/2023 4

Introduction
 Un algorithme doit donc contenir uniquement
des instructions compréhensibles par celui
qui devra l’exécuter.
24/02/2023 5

Définition
 Algorithmique:
◦ Définition1: désigne l'ensemble des règles et
des techniques qui sont impliquées dans la
définition et la conception des algorithmes.
◦ Définition2: l'algorithmique c'est de savoir
comment lire, écrire, évaluer et optimiser des
algorithmes.
24/02/2023 6

Définition
 Algorithme:
◦ Définition1: Un algorithme décrit une
méthode de résolution de problème
programmable sur machine.
◦ Définition2 : Un algorithme est un ensemble
d'opérations de calcul élémentaires, organisé
selon des règles précises dans le but de
résoudre un problème donné. Pour chaque
donnée du problème, l'algorithme retourne
une réponse après un nombre fini
d'opérations(+, -,/,<,>,... ).
24/02/2023 7

Définition
 Qu’est-ce qu’un programme?
◦ Un programme est donc une suite d'instructions
exécutées par la machine. La machine a son propre
langage appelé langage machine.
◦ Un programme est l’expression d’un algorithme par une
machine donnée dans un langage de programmation
donné en utilisant le répertoire d’actions(opérations,
instructions) et les règles de composition propres à
cette machine et à ce langage donnés.
◦ Un programme est un assemblage et un enchaînement
d’instructions élémentaires écrit dans un langage de
programmation, et exécuté par un ordinateur afin de
traiter les données d’un problème et renvoyer un ou
plusieurs résultats.
24/02/2023 8

Méthodologie
 Pour résoudre un problème, il est vivement conseillé de
réfléchir d'abord à l'algorithme avant de programmer.
 Exemple de construction d’algorithme:
◦ Exemple: calcul des racines de l’équation du second ordre
ax2+bx+c=0
◦ 1ère version:
 Lire a, b, c
 Calculer les racines de l’équation
 Imprimer les racines
24/02/2023 9

Méthodologie
 La résolution d’un problème est
caractérisé par 4 étapes :
◦ Comprendre la nature du problème posé
◦ Préciser les données fournies (Entrées)
◦ Préciser les résultats que l’on désire obtenir
(Sorties)
◦ Déterminer le processus de transformation
des données en résultats.
24/02/2023 10

Méthodologie
 Comment on programme?
24/02/2023 11
On utilise un pseudo-langage, comportant toutes les
structures de base d'un langage de programmation
On traduit notre "pseudo" en langage évolué
en fonction des possibilités de ce langage
Ce langage sera ensuite traduit en langage machine

Méthodologie
 Un programme est donc une suite
d'instructions exécutées par la machine.
Ces instructions peuvent:
◦ soit s'enchaîner les unes après les autres, on
parle alors de séquence d'instructions;
◦ ou bien s'exécuter dans certains cas et pas dans
d'autres, on parle alors de structure
alternative;
◦ ou se répéter plusieurs fois, on parle alors de
structure répétitive.
24/02/2023 12

La séquence d’instructions
 Une instruction est une action que
l'ordinateur est capable d'exécuter.
 Une séquence d'instruction serait :
◦ Se lever
◦ Prendre sa douche
◦ Prendre le petit déjeuner
◦ S'habiller
24/02/2023 13

Structures Alternatives
 Une alternative s'exprime par si …
Sinon…
◦ Si fin de semaine ou congé
 Mettre sa tenue de sport
 Faire son jogging
◦ Sinon
 Mettre sa tenue de travail
 Aller travailler
◦ Fin Si
24/02/2023 14

Structure répétitive
 La routine journalière d’un employé est :
◦ Ouvrir guichet
◦ Appeler premier client
◦ TantQue " client dans file d'attente " et " pas fin
de journée "
 Traiter client
 Appeler client suivant
◦ FinTantQue
 Les deux actions "Traiter client" et "Appeler
client suivant" vont se répéter tant que la
condition située derrière l'instruction "Tant que"
est vérifiée.
24/02/2023 15

Pourquoi faire des
algorithmes
 la rédaction des algorithmes permet
plusieurs choses :
◦ d'être compréhensible par tout informaticien
même s'il ne connait pas le langage du
programme
◦ de vérifier la complexité du programme et donc
de l'optimiser
◦ de faire ressortir de manière compréhensible
les cas d'utilisations
24/02/2023 16

NOTIONS DE BASE
Comment faire des algorithmes?
Les variables
Le type de la variable
Les instructions
Syntaxe général de l’algorithme
Les structures de contrôle
Structure répétitive
Les tableaux
Organigramme
Procédures & Fonctions
Récursivité
24/02/2023 17

Comment faire des algorithmes
 les algorithmes sont rédigés dans un langage à mi-
chemin entre le français et les langages de
programmation, dit pseudo-code .
 En programmation, le pseudo-code est une façon de
décrire un algorithme sans référence à un langage de
programmation particulier. L'écriture en pseudo-code
permet souvent de bien prendre toute la mesure de la
difficulté de l'implémentation de l'algorithme, et de
développer une démarche structurée dans la
construction de celui-ci.
24/02/2023 18

Comment faire des
algorithmes(suite)
 La raison d’être d’un algorithme est de
résoudre un problème. La plus grande
attention doit être portée à la
compréhension du problème, faute de quoi
l’algorithme n’a aucune chance d’être
correct. Le langage utilisé pour la définition
d’un problème est un langage scientifique
utilisant pour des raisons de simplicité une
langue naturelle(français par exemple).
24/02/2023 19

Les variables
Une variable est un objet dont la valeur
n’est pas invariable
Une variable peut être représentée par une
case mémoire, qui contient la valeur d'une
donnée.
Chaque variable possède un nom unique
appelé identificateur par lequel on peut
accéder à son contenu.
◦Par exemple, on peut avoir en mémoire une
variable prix et une variable quantité.
24/02/2023 20

Les variables(suite)
 Une variable possède 3 attributs :
◦ Une valeur
◦ Un nom(invariable) qui sert à la désigner
◦ Un type(invariable) qui décrit l’utilisation
possible de la variable
 Une valeur
◦ la valeur d'une variable(contenu) peut varier
au cours du programme. L'ancienne valeur
est tout simplement écrasée et remplacée par
la nouvelle.
◦ La valeur peut être de différents types et de
tailles différentes.
24/02/2023 21

 Nom de la variable
◦ C’est une suite de lettres et de chiffres
commençant nécessairement par une lettre
◦ Le nombre maximal de caractères imposé varie
selon les langages
◦ La lisibilité des programmes dépend de l’habilité
à choisir des noms représentatifs
◦ Le nom de la variable doit être le plus
représentatif possible du contenu de celle-ci pour
faciliter la lecture de l'algorithme. En revanche, il
ne doit pas non plus être trop long pour ne pas
nuire à la lisibilité de l'ensemble.
24/02/2023 22

 Nom de la variable
◦ Exemple
 Je veux mémoriser l'âge d'une personne dans une variable,
j'ai le choix de l'appeler :
 a
 âge
 age
 ageDeLaPersonneDontJeSuisEntrainDeParler
◦ Remarque :
 Le premier cas est trop court, si je n'ai pas lu la description
plus haut, je suis totalement perdu. Le deuxième cas ne
convient pas non plus car on évitera tout caractère accentué
dans les noms de variable. Le dernier cas est certes très
précis, mais tellement long qu'il en devient illisible. Bref, le
troisième cas semble le plus approprié
24/02/2023 23

 Type de la variable
◦ Le type de la variable définit :
 La nature des informations qui seront représentées dans la
variable
 Les limitations concernant les valeurs à représenter
 Les opérations réalisables avec les variables
correspondantes.
◦ Propriété : Une variable doit être déclaré avant son
utilisation
24/02/2023 24

◦ Entier : il s'agit des variables destinées à
contenir un nombre entier positif ou négatif.
◦ Réel : il s'agit des variables numériques qui ne
sont pas des entiers, c'est à dire qui
comportent des décimales
◦ Caractère : Les variables de type caractère
contiennent des caractères alphabétiques ou
numériques seul(ex: ‘c’)
◦ Booléen : Les variables qui prennent les
valeurs (vrai ou faux) ou les valeurs (oui ou
non).
24/02/2023 25

◦ Chaîne de caractères : représentant un
texte, contenant un ou plusieurs
caractères(ex: ’’Bonjour tout le monde’’)
◦ Tous les traducteurs de langages prennent en
compte cette notion de type par des instructions de
déclaration de type
◦ Exemple:
Variable Moyenne : réel;(Moyenne en numérique)
Variable NbreEtudiant : entier; (NbreEtudiant en
numérique)
Variable c1, lettre, z : caractère;
24/02/2023 26

 Type de la variable: Constante
◦ Définitions : une constante est un objet de
valeur invariable. Elle est la réalisation
d’une valeur de type particulier.
◦ Exemple:
 Constante Zero=0: entier;
( Max:entier)100;
24/02/2023 27

 Les opérateurs de l’algorithmique
24/02/2023 28
Type Exemple Opération possibles symbole
Réel -15.69, 0.49 Addition
Soustraction
Multiplication
Division
Exposant
Pourcentage
comparaisons
+
-
*
/
^
%
<,<=,>,>=,=,…
Entier -10, 4, 768 Addition
Soustraction
Multiplication
Division
Modulo
Exposant
Pourcentage
+
-
*
DIV
MOD
^
%

 Les opérateurs de l’algorithmique
24/02/2023 29
Type Exemple Opération
possibles
symbole
caractère ‘B’, ‘n’ comparaisons <,<=,>,>=,=,…
Booléen Vrai, Faux Comparaison
Négation
Conjonction
disjonction
<,<=,>,>=,=,…
NON
ET
OU

Les instructions
 L’instruction d’affectation
◦ L’instruction d’affectation permet de manipuler les
valeurs des variables. Son rôle consiste à placer
une valeur dans une variable.
◦ Notation X=Y ou bien X:=Y ou bien XY
◦ Exemple :
1. affecter une valeur à une variable
 X:=5, On charge la variable X avec la valeur 5
2. Affecter le contenu d’une variable à une autre
variable
 X:=Y , On charge X avec le contenu de Y
 Y représente :
 Constante ou Nom d’une variable ou Expression
logique
 X et Y doivent être de même type
24/02/2023 30

Les instructions(suite)
 L’instruction d’affectation
3. Affecter une formule à une variable
 X:= X + 2 * Y
On charge la variable X par la valeur du résultat
de la formule et on écrase sa valeur initiale
X Y
24/02/2023 31
3
11
4

Les instructions(suite)
 Les instructions d’Entrée/Sortie
◦ Un programme est amené à :
 Prendre des données par le périphérique(clavier) : rôle de
l’instruction de lecture
 Communiquer des résultats par l’intermédiaire du
périphérique(écran) : rôle de l’instruction de l’écriture
◦ Instruction de lecture
 Rôle : fournir des données au programme
 Syntaxe : Lire(variable)
 Exemple : Lire( X) on saisie une valeur pour la stocker après
dans la variable X
◦ Instruction d’écriture
 Rôle : fournir des résultats directement compréhensibles
 Syntaxe : Ecrire( variable), Ecrire(’’chaine de caractères’’)
 Exemple : Ecrire(X), Ecrire(’’Bonjour’’)
24/02/2023 32

Syntaxe général de l’algorithme
 Le moule d’un algorithme
◦ Un algorithme comportera :
 Une partie déclaration
 Une partie encadrée par ’’début’’ ’’ fin’’ où sont
décrites les actions
Algorithme Nom_de_l_algorithme :
Déclaration;
Debut
Actions;
Fin
24/02/2023 33

Syntaxe général de
l’algorithme(suite)
 Le moule d’un algorithme
◦ Dans la partie déclarations, nous trouvons :
 Déclaration de constantes
 déclaration de variables
 déclaration de fonctions
◦ Dans la partie actions, nous trouvons :
 suite d'instructions
 Structure alternative
 Structure répétitive
24/02/2023 34

Syntaxe général de
l’algorithme(suite)
 Exemple :
Algorithme toto
/* les constantes: il est obligatoire de leur donner une valeur dès
leur déclaration */
CONST titi  10 : entier
tutu  "bonjour!" : chaîne
// les variables au sens strict
VAR riri, fifi : réels
loulou : chaîne
Debut
<Instruction1>;
<Instruction2>;
….
<Instruction3>;
Fin
24/02/2023 35
déclarations
Corps de l’algorithme

Exercices : Instructions
 Exercice 1:
Écrire un algorithme qui permet de saisir des
valeurs pour A et B , faire la somme et
afficher le résultat?
 Exercice 2:
Écrire un algorithme qui permet de calculer et
afficher la surface d’un cercle?
24/02/2023 37

Exercices : Instructions(suite)
 Exercice 3
Écrire un algorithme qui permet de calculer et
afficher le salaire brut d’un ouvrier connaissant
le nombre d’heure et le tarif d’horaire?
 Exercice 4
Écrire un algorithme qui fait la conversion
d’une somme d’argent donnée en DH, en une
somme d’argent en Euro?
24/02/2023 38

Les structures de contrôles
 Le branchement conditionnel
Le branchement conditionnel Aide à Structurer un
ensemble d’instructions
24/02/2023 39
Syntaxe 1 :
Si <conditions> alors
<Instruction1>
…
<Instruction N>
Fsi
Exemple :
Si (a<b) alors
maxb;
mina;
Fsi

Les structures de contrôles(suite)
 Le branchement conditionnel
24/02/2023 40
Syntaxe :
Si <expression booléenne> alors
<Instruction1>
…
<Instruction N>
Sinon
<Instruction1>
…
<Instruction N>
Fsi
Exemple :
Si (a<b) alors
maxb
Sinon
maxa
Fsi

Les structures de contrôles(suite)
 Qu’est ce qu’une condition ?
◦ une condition est composée de trois éléments :
 une valeur, un opérateur de comparaison, une autre
valeur
◦ Les valeurs peuvent être a priori de n’importe quel
type (numériques, caractères…). Mais si l’on veut
que la comparaison ait un sens, il faut que les deux
valeurs de la comparaison soient du même type !
◦ Les opérateurs de comparaison sont :
 = égal à, <> différent de
 < strictement plus petit que, > strictement plus grand
que, <= plus petit ou égal à, >= plus grand ou égal
à…
24/02/2023 41

Les structures de
contrôles(suite)
 Exemple:
◦ ‘t’ < ‘w’ VRAI
5>6 FAUX
2< 3 VRAI
 Exercice:
◦ Écrire un algorithme qui demande un nombre
à l’utilisateur, et l’informe ensuite si ce nombre
est positif ou négatif (on laisse de côté le cas
où le nombre vaut zéro).
24/02/2023 42

Les structures de
contrôles(suite)
 Conditions composées:
◦ Certains problèmes exigent parfois de formuler des
conditions composées liées entre eux par les
opérateurs logiques suivants : ET, OU, NON, et
XOR.
 Condition1 ET Condition2 : VRAI, si Condition1 est
VRAI et Condition2 est VRAI.
 Condition1 OU Condition2 : VRAI, si Condition1 est
VRAI ou bien Condition2 est VRAI.
 Le XOR (ou OU exclusif)
 Condition1 XOR Condition2 : VRAI, si Condition1 est VRAI, ou
bien Condition2 est VRAI.
 Mais si toutes les deux sont fausses, ou que toutes les deux
sont VRAI, alors le résultat global est considéré comme FAUX.
24/02/2023 43

Les structures de
contrôles(suite)
◦ le NON inverse une condition : NON(Condition1) est
VRAI si Condition1 est FAUX, et il sera FAUX si
Condition1 est VRAI.
◦ tables de vérité (C1 et C2 représentent deux
conditions, et on envisage à chaque fois les quatre
cas possibles) :
24/02/2023 44
C1 et C2 C2 Vrai C2 Faux
C1 Vrai Vrai Faux
C1 Faux Faux Faux
C1 ou C2 C2 Vrai C2 Faux
C1 Vrai Vrai Vrai
C1 Faux Vrai Faux

Les structures de
contrôles(suite)
 Exercice :
◦ Écrire un algorithme qui demande deux
nombres à l’utilisateur et l’informe ensuite si
leur produit est négatif ou positif (on laisse de
côté le cas où le produit est nul). Attention
toutefois : on ne doit pas calculer le produit
des deux nombres.
24/02/2023 45
C1 xor C2 C2 Vrai C2 Faux
C1 Vrai Faux Vrai
C1 Faux Vrai Faux
Non C1
C1 Vrai Faux
C1 Faux Vrai

Exercices : structures de
contrôles
 Exercice 1:
◦ On désire comparer deux valeurs ,Écrire un
algorithme qui affiche la plus grande des deux?
 Exercice 2:
◦ Écrire un algorithme qui affiche le salaire brut d’un
ouvrier sachant que les heures supplémentaires
de 172 heures sont payées à 50% de tarifs
d’horaire en plus?
24/02/2023 46

contrôles
 Exercice 4:
Calculer le montant de la facture d’un client ayant
commandé une quantité d’un produit avec un prix
unitaire hors taxe
 Le taux de T.V.A est : 20%
 Les frais de transport sont 0.8 DH de Km , Le client est
disposé du frais de transport si le montant est supérieur
4500 DH
 Exercice 5:
Une bibliothèque fait des réductions sur l’achat des
livres :
 25% pour les étudiants.
 15% pour les enseignants
Écrire un algorithme qui calcule et affiche le prix à payer
24/02/2023 47

contrôles
 Exercice 6:
Écrire un algorithme qui calcule et affiche le
maximum de trois nombre A,B et C ?
 Exercice 7:
Écrire un algorithme qui permet de résoudre
l’équation du premier degré : aX+b=0?
 Exercice 8:
Écrire un algorithme qui permet de résoudre
une équation de second degré : aX²+bX+c=0 ?
24/02/2023 48

contrôles
 Exercice 9:
Écrire un algorithme qui lie trois nombre A,B et C , puis
il détermine si l’un est égal à la somme de 2 autres
sinon il affiche un message « pas de solution »?
24/02/2023 49

Les structures de
contrôles(suite)
 Le choix multiple
Variable i:entier;
Lire(i);
Selon que
i=1 : faire <instruction1>
Ou que i=2 : faire <instruction2>
Ou que i=3 : faire <instruction3>
Autrement écrire(’’mauvais choix’’)
Fselonque
24/02/2023 50

contrôles
 Exercice 10:
Écrire un algorithme qui à partir d’un nombre
compris entre 1 et 7 affiche le jour
correspendant?
24/02/2023 51

Les structures de
contrôles(suite)
 Tests imbriqués:
◦ un algorithme doit donner l’état de l’eau selon
sa température il doit choisir entre trois
réponses possibles (solide, liquide ou vapeur).
Variable Temp : Entier
Début
Ecrire (“Entrez la température de l’eau :”)
Lire (Temp)
Si Temp <= 0 Alors
Ecrire (“C’est de la glace“)
Finsi
Si Temp > 0 Et Temp < 100 Alors
Ecrire (“C’est du liquide”)
Finsi
Si (Temp > 100 )Alors
Ecrire “C’est de la vapeur”
Finsi
Fin
24/02/2023 52

Les structures de
contrôles(suite)
 Tests imbriqués: deuxième solution qui
imbrique le test
Variable Temp : Entier
Début
Lire (Temp)
Si Temp =< 0 Alors
Ecrire (“C’est de la glace“)
Sinon
Si Temp < 100 Alors
Ecrire( “C’est du liquide”)
Sinon
Ecrire( “C’est de la vapeur”)
Finsi
Finsi
Fin
24/02/2023 53

Les structures de
contrôles(suite)
 Exercice:
◦ Écrire un algorithme qui demande l’âge d’un
enfant à l’utilisateur. Ensuite, il l’informe de sa
catégorie :
- « Poussin » de 6 à 7 ans
- « Pupille » de 8 à 9 ans
- « Minime » de 10 à 11 ans
- « Cadet » après 12 ans
Peut-on concevoir plusieurs algorithmes
équivalents menant à ce résultat ?
24/02/2023 54

Les structures de
contrôles(suite)
 Variables Booléennes:
◦ Il existe des variables (les booléennes)
susceptibles de stocker les valeurs VRAI ou
FAUX. On peut donc entrer des conditions
dans ces variables, et tester ensuite la valeur
de ces variables.
◦ Exemple:
 Variable Temp : Entier
Variables A, B : Booléen
Début
Lire (Temp)
A ← Temp <= 0
B ← Temp < 100 24/02/2023 55

Les structures de
contrôles(suite)
◦ Si A Alors
Ecrire( “C’est de la glace“)
Sinon
Si B Alors
Ecrire “C’est du liquide”
Sinon
Ecrire “C’est de la vapeur”
Finsi
Finsi
Fin
 Dans une condition composée employant à la fois
l’opérateur ET et l’opérateur OU, la présence de
parenthèses possède une influence sur le résultat.
24/02/2023 56

Exercice: Les structures de
contrôles
 Ecrivez un algorithme qui lira au clavier
l’heure et les minutes, et il affichera
l’heure qu’il sera une minute plus tard.
 Par exemple, si l'utilisateur tape 21 puis
32, l'algorithme doit répondre : "Dans une
minute, il sera 21 heure(s) 33".
 NB : on suppose que l'utilisateur entre une
heure valide. Pas besoin donc de la
vérifier.
24/02/2023 57

 A quoi cela sert-il donc ?
◦ Prenons le cas d’une saisie au clavier (une
lecture), où par exemple, le programme pose
une question à laquelle l’utilisateur doit
répondre par O (Oui) ou N (Non). Mais tôt ou
tard, l’utilisateur, risque de taper autre chose
que la réponse attendue.
◦ Alors, dans tout l’algorithme on met en place
ce qu’on appelle un contrôle de saisie, afin
de vérifier que les données entrées au clavier
correspondent bien à celles attendues par
l’algorithme.
24/02/2023 58

Structure répétitive(suite)
◦ On pourrait essayer avec une structure de
contrôle SI.
◦ Variable Rep : Caractère
Début
Ecrire (“Voulez vous un café ? (O/N)“)
Lire (Rep)
Si Rep <> “O“ ET Rep <> “N” Alors
Ecrire( “Saisie erronnée. Recommencez“)
Lire (Rep)
FinSi
Fin
◦ 24/02/2023 59

◦ Si l’utilisateur ne se trompe qu’une seule fois,
et entre une valeur correcte à la deuxième
demande, c’est parfait.
◦ Par contre, s’il commet une deuxième erreur, il
faudrait rajouter un SI. Et ainsi de suite, on
peut rajouter des centaines de SI, et écrire un
algorithme lourd.
◦ La solution consistant à aligner des SI n’est
pas correcte dans ce cas. La seule issue est
d’utiliser une structure de boucle.
24/02/2023 60

◦ Qui ce présente ainsi: TantQue booléen Faire
…
Instructions
…
FinTantQue
 Le principe est simple : l’algorithme arrive sur la ligne du
TantQue. Il examine alors la valeur du booléen (qui, je le
rappelle, peut être une variable booléenne ou, plus
fréquemment, une condition). Si cette valeur est VRAI,
l’algorithme exécute les instructions qui suivent, jusqu’à
ce qu’il rencontre la ligne FinTantQue. Il retourne ensuite
sur la ligne du TantQue, procède au même examen, et
ainsi de suite. Le cycle ne s’arrête que lorsque le booléen
prend la valeur FAUX.
24/02/2023 61

◦ Illustration avec notre problème de contrôle de
saisie. Une première approximation de la solution
consiste à écrire :
Variable Rep :Caractère
Début
lire(Rep)
TantQue Rep <> “O“ ET Rep <> “N“ Faire
Lire (Rep)
FinTantQue
Fin
24/02/2023 62

◦ Une deuxième approximation de la solution, avec
affectation, consiste à écrire :
Variable Rep :Caractère
Début
Rep ← “X“
TantQue Rep <> “O“ ET Rep <> “N“ Faire
Lire (Rep)
FinTantQue
Fin
◦ Cette manière de procéder est à connaître, car
elle est employée très fréquemment.
24/02/2023 63

 Structure répétitive, dite aussi itérative
ou boucle permet, de répéter une ou
plusieurs actions un certain nombre de
fois. On identifie en règle générale 3
types de répétitive :
◦ TantQue
◦ Répéter Jusqu'à
◦ Pour
24/02/2023 64

 Tant que
 Les répétitives où la condition d’arrêt
est placée au début.
◦ Syntaxe :
Tant que <expression logique> faire
<séquence d’instructions>
Ftantque
TantQue condition
actions
FTantQue
 Ce qui signifie : tant que la condition est
vraie, on exécute les actions.
24/02/2023 65

Exercices
1. Ecrire un algorithme qui demande à l’utilisateur un
nombre compris entre 1 et 3 jusqu’à ce que la
réponse convienne.
2. Ecrire un algorithme qui demande un nombre
compris entre 10 et 20, jusqu’à ce que la réponse
convienne. En cas de réponse supérieure à 20, on
fera apparaître un message : « Plus petit ! », et
inversement, « Plus grand ! » si le nombre est
inférieur à 10.
3. Écrire un algorithme qui demande un nombre de
départ, et qui ensuite affiche les dix nombres
suivants. Par exemple, si l'utilisateur entre le
nombre 17, le programme affichera les nombres de
18 à 27.
24/02/2023 67

 Boucler en comptant, ou compter en
bouclant
◦ Il arrive très souvent qu’on ait besoin
d’effectuer un nombre déterminé de passages.
Or, a priori, notre structure TantQue ne sait
pas à l’avance combien de tours de boucle
elle va effectuer:
◦ C’est pourquoi une autre structure de boucle
est à notre disposition :
 la structure : Pour
24/02/2023 68

 Variable Num1 : Entier
Début
Num1 ← 0
TantQue Num1 < 15 Faire
Num1 = Num1 + 1
Ecrire (“Passage
numéro : “, Num1)
FinTantQue
Fin
 Variable Num1 : Entier
Début
Pour Num1 = 1 à 15
Faire
Ecrire( “Passage
numéro : “, Num1)
Num1 Suivant
Fin
24/02/2023 69
la structure :Pour est un cas particulier de TantQue :
celui où le programmeur peut dénombrer à l’avance le
nombre de tours de boucles nécessaires.

 Pour
◦ Les répétitives où le nombre d’itération est
fixée une fois pour toute.
◦ Syntaxe :
 Pour Compteur = Initial à Final Pas
ValeurDuPas
…
Instructions
…
Compteur suivant (n’est pas indispensable)
FPour
24/02/2023 70

 la progression du compteur est laissée à votre libre
disposition. Dans la plupart des cas, on a besoin d’une
variable qui augmente de 1 à chaque tour de boucle. On
ne précise alors rien à l’instruction « Pour » ; celle-ci, par
défaut, comprend qu’il va falloir procéder à cette
incrémentation de 1 à chaque passage, en commençant
par la première valeur et en terminant par la deuxième.
 Si vous souhaitez une progression plus spéciale, de 2
en 2, ou de 3 en 3, ou en arrière, de –1 en –1, ou de –10
en –10, il faut préciser à votre instruction « Pour » en lui
rajoutant le mot « Pas » et la valeur de ce pas.
 Quand on met un pas négatif dans une boucle, la valeur
initiale du compteur doit être supérieure à sa valeur
finale si l’on veut que la boucle tourne !
24/02/2023 71

 Les structures TantQue sont employées dans
les situations où l’on doit procéder à un
traitement sur les éléments d’un ensemble dont
on ne connaît pas d’avance la quantité, comme
par exemple :
◦ le contrôle d’une saisie.
◦ la gestion des tours d’un jeu (tant que la partie
n’est pas finie, on recommence).
 Les structures Pour sont employées dans les
situations où l’on doit procéder à un traitement
sur les éléments d’un ensemble dont on connaît
d’avance la quantité.
24/02/2023 72

 Des boucles imbriquées:
◦ De même que qu’une structure SI … ALORS
peut contenir d’autres structures SI … ALORS,
une boucle peut tout à fait contenir d’autres
boucles.
Variables Num1, Num2 : Entier
Pour Num1 ← 1 à 15
Ecrire (“Il est passé par ici“)
Pour Num2 ← 1 à 6
Ecrire (“Il repassera par là“)
Fpour
FPour
◦
24/02/2023 73

 Répéter..Jusqu’à :
◦ la condition d’arrêt est placée à la fin
◦ Syntaxe :
Répéter
<séquence d’instructions>
Jusqu’à <expression logique>
Frépéter
◦ Exemple :
Num1:=1
Répéter
Ecrire (“Passage numéro : “, Num1)
Num1 = Num1 + 1
Jusqu’à (Num1 >= 15 )
24/02/2023 74

Exercices
1. Écrire un algorithme qui saisie N entier et
affiche leur somme et leur moyenne ?
2. Écrire un algorithme pour calculer et afficher la
somme et la moyenne de100 premiers nombres
entiers ?
3. Écrire un algorithme qui permet de calculer S1,
S2,S3,S4,S5,S6 tel que:
◦ S1 = 1 + ½ + 1/3 + ¼ +……..1/N
◦ S2 = 1 + ½ + ¼ + 1/6 +……..1/N
◦ S3 = 1 + 1/3 + 1/5 +……..1/N
◦ S4 = 1 - ½ + ¼ - 1/6……..1/N
◦ S5 = 1 + x+x²……..xN
◦ S6 = 1 + x+x²/2…….. xN /N
24/02/2023 76

Exercices
4. Ecrire un algorithme qui vérifie si un
nombre est premier où pas ?
5. écrire un algorithme qui saisit deux entiers,
calcule et affiche la somme de ces 2 entiers
(on arrête la saisie avec la valeur 0) ?
6. Ecrire un algorithme qui permet de
calculer le factoriel d’un nombre positif ?
24/02/2023 77

Devoir N° 1
 Une salle de cinéma désire automatiser la gestion de la
billetterie pour chaque client qui se présente, on calcule le
prix du billet en fonction des données suivantes:
◦ NF : Numéro du film
◦ Age : Age de spectateur
 Le prix normal de la facture est de 30 DH, cependant des
remises peuvent être accorder en fonction du critères
suivants :
◦ NF=2 ou Age < 15 remise de 50%
◦ NF=2 et Age >75 remise 25%
◦ NF=3 et Age < 15 entrée refusée
 Écrire un algorithme qui permet de calculer et décider le
prix à payer pou chaque client qui se présente . on arrête
la saisie par "non"
24/02/2023 78

Devoir N°2
 Une entreprise désire automatisée la gestion de
paie de son personnel. Pour chaque employé,
on doit introduire le nom, le prénom, le salaire de
base(SB), le nombre d'enfant et
l'ancienneté(ANC).
 Un prix de 100 DH est accordé pour
chaque enfant .
◦ Si ancienneté<=10 ans et SB < 1000 DH une prime de
50% du SB
◦ Si l'ancienneté est 10 ans < ANC <20 ans et SB >
1000 DH prime de 70% du SB
 Calculer le salaire brute (SB+ le prime + les
enfants) et afficher le nom, prénom, l'ancienneté
24/02/2023 79

Les tableaux
 Supposons que nous avons besoin de
calculer la moyenne de 12 notes d’un
étudiant.
 la seule solution dont nous disposons
consiste à déclarer douze variables,
appelées par exemple: X1, X2, X3,…X12.
 La première étape est de lire les valeurs
de toute ces variables une par une, ce qui
nous fait douze instructions de lecture et
après calculer la moyenne par l’instruction:
 Moy ← (X1+X2+X3+X4+X5+NX6+X7+X8+X9+X10+X11+X12)/12
24/02/2023 80

Les tableaux(suite)
 C’est pourquoi l’algorithmique (la
programmation) nous permet de
rassembler toutes ces variables en une
seule, au sein de laquelle chaque valeur
sera désignée par un numéro.
24/02/2023 81
Un ensemble de valeurs portant le même nom de variable et repérées par
un nombre, s’appelle un tableau, ou encore une variable indicée.
Le nombre qui, au sein d’un tableau, sert à repérer chaque valeur
s’appelle l’indice.
Chaque fois que l’on doit désigner un élément du tableau, on fait figurer
le nom du tableau, suivi de l’indice de l’élément, entre parenthèses.
Ex: Nom_tableau(5)

Les tableaux(suite)
 Notation et utilisation algorithmique
◦ Dans notre exemple, nous créerons donc un
tableau appelé Note.
◦ Tableau Note(12) : Entier
◦ On peut créer des tableaux contenant des
variables de tous types : tableaux de
numériques, tableaux de caractères, tableaux
de booléens, tableaux de tout ce qui existe
dans un langage donné comme type de
variables.
◦ L’énorme avantage des tableaux, c’est qu’on
va pouvoir les traiter en faisant des boucles.
24/02/2023 82

Les tableaux(suite)
 Notation et utilisation algorithmique
Tableau Note(12) : Entier
Variables i, Som : Entier
Variable Moy : Réel
Pour i ← 0 à 11
Ecrire (“Entrez la note n°”, i)
Lire( Note(i))
FPour
Som ← 0
Pour i ← 0 à 11
Som = Som + Note(i)
Fpour
Moy = Som / 12 24/02/2023 83

Les tableaux(suite)
 Remarque générale : l’indice qui sert à
désigner les éléments d’un tableau peut être
exprimé directement comme un nombre en clair,
mais il peut être aussi une variable, ou une
expression calculée.
 La valeur d’un indice doit toujours :
◦ être égale au moins à 0 (dans quelques rares
langages, le premier élément d’un tableau porte
l’indice 1). Mais nous avons choisi ici de commencer
la numérotation des indices à zéro, comme c’est le
cas en langage C.
◦ être un nombre entier. Quel que soit le langage.
◦ être inférieure ou égale au nombre d’éléments du
tableau (moins 1, si l’on commence la
24/02/2023 84

Exercices
 Écrire un algorithme qui déclare et
remplisse un tableau de 7 valeurs
numériques en les mettant toutes à zéro.
 Écrire un algorithme qui déclare et
remplisse un tableau contenant les six
voyelles de l’alphabet latin.
 On saisit des entiers et on les range dans
un tableau (maximum 50) Écrire un
programme qui affiche le maximum, le
minimum et la valeur moyenne de ces
nombres.
24/02/2023 85

Exercices
 Écrivez un algorithme permettant à
l’utilisateur de saisir un nombre
quelconque de valeurs, qui devront être
stockées dans un tableau. L’utilisateur doit
donc commencer par entrer le nombre de
valeurs qu’il compte saisir. Il effectuera
ensuite cette saisie. Enfin, une fois la
saisie terminée, le programme affichera le
nombre de valeurs négatives et le nombre
de valeurs positives.
24/02/2023 86

Exercices
 Que produit l’algorithme suivant ?
Tableau Nb(6) : Entier
Variable i en Entier
Début
Pour i ← 0 à 5
Nb(i) ← i * i
FPour
Pour i ← 0 à 5
Écrire Nb(i)
FPour
Fin
 Peut-on simplifier cet algorithme avec le même
résultat ? 24/02/2023 87

Exercices
 Que produit l’algorithme suivant ?
Tableau N(7) en Entier
Variables i, k en Entier
Début
N(0) ← 1
Pour k ← 1 à 6
N(k) ← N(k-1) + 2
FPour
Pour i ← 0 à 6
Ecrire N(i)
FPour
Fin
 Peut-on simplifier cet algorithme avec le même
24/02/2023 88

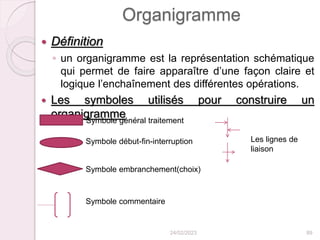
Organigramme
 Définition
◦ un organigramme est la représentation schématique
qui permet de faire apparaître d’une façon claire et
logique l’enchaînement des différentes opérations.
 Les symboles utilisés pour construire un
organigramme
24/02/2023 89
Symbole général traitement
Symbole début-fin-interruption
Symbole embranchement(choix)
Symbole commentaire
Les lignes de
liaison

Organigramme
24/02/2023 90
Exemple :
Condition
Instruction 1
Instruction 2
suite

Organigramme
24/02/2023 91
Exemple :Le branchement conditionnel
instruction1
conditio
n
instruction2

Organigramme
24/02/2023 92
Exemple :Structure répétitive
instruction
conditio
n
V
F

Organigramme
24/02/2023 93
Exemple : Structure répétitive
instruction
conditio
n
F
V

Notions de sous-algorithme
 Définition
◦ Un sous-algorithme est un élément d’algorithme
nommé et éventuellement paramétré que l’on définit
afin de pouvoir ensuite l’appeler par son nom en
affectant, s’il y a lieu, des valeurs aux paramètres.
◦ Intérêt :
 Réaliser un découpage d’une tâche en sous-tâche.
 Effectuer une seule description d’une tâche commune
 Concevoir une application de manière descendante en
entrant de plus en plus dans les détails
◦ Structure : un sous-algorithme est composé
 D’une tête nom sous-algorithme, paramètres(arguments)
avec leur type
 D’un corps des déclarations d’objets locaux aux sous-
algorithme, instructions à exécuter
24/02/2023 94

Notions de sous-algorithme
◦ Sous-algorithme Nom(liste des paramètres)
déclarations des variables locales
Début
Corps du sous-algorihtme
Fin
◦ Algorithme Nom
Déclaration des variables
Début
Instructions
Appel du sous-algorithme
Instructions
Fin
24/02/2023 95

Procédures & Fonctions
 Procédures
◦ Syntaxe
Procédure nom_procédure(var:type;var:type)
Variable interne
Début procédure
Instructions
Finprocédure
24/02/2023 96

Procédures & Fonctions
 Fonctions
◦ Syntaxe
Fonction nom_fonction(var:type;var:type):type
Variable interne;
Début fonction
Instructions;
Retourner variable;
Fin fonction
24/02/2023 97

Procédure & Fonction
Rep1,Rep2 : caractère
Fonction RepOuiNon() : caractères
variable Rep ← ""
TantQue Rep <> "Oui" et Rep <> "Non"
Ecrire( "Tapez Oui ou Non")
Lire (Rep)
FinTantQue
Renvoyer Rep
Fin
Début
Ecrire( "Etes-vous marié ?")
Rep1 ← RepOuiNon()
Ecrire( "Avez-vous des enfants ?" )
Rep2 ← RepOuiNon()
Fin
24/02/2023 98

Exercices
 EX0
◦ Ecrire un algorithme qui lit une valeur qlq x et qui
détermine la valeur de l’expression :
1+x+x2+…+x20
 EX1
◦ Ecrire une procédure qui lit N éléments en
paramètre et retourne la somme de ces
éléments dans une variable somme.
 EX2
◦ Ecrire une fonction entière statistique qui lit
100 notes et retourne le nombre de notes
comprises entre 10 et 20 compris
24/02/2023 100

Exercices
 EX3
◦ Ecrire un algorithme qui permet de faire les
traitements suivants :
Soit un tableau T de N entiers
1. Remplir les N cases du tableau
2. Compter le nombre des éléments non nuls
3. Trouver le plus grand éléments du tableau
et le mettre dans la variable MAX
4. Rechercher la place du plus petit élément et
le mettre dans la variable position.
24/02/2023 101

Exercices
 EX4
◦ Ecrire un algorithme qui cherche dans un
tableau non trié si un nombre x existe au
moins une fois.
 EX5
◦ Ecrire un algorithme qui cherche dans un
tableau trié si un nombre x existe au moins
une fois.
 EX6
◦ Ecrire un algorithme qui permet de lire les
âges de 25 stagiaires(ils ont au moins 23ans
et au plus 30ans) et fournit le nombre de
stagiaires de chacun des âges.
24/02/2023 102

Exercices
 EX7
◦ Le tableau factures contient N constantes de
factures, le tableau PAYES de N booléens
indique si chacune des factures a été réglées ou
pas, on veut recopier séquentiellement dans un
3ème tableau RESTESAPAYES, les sommes
restant dues.
24/02/2023 103

Récursivité
 Un algorithme est dit récursif lorsqu’il intervient
dans sa description, c’est-à-dire lorsqu’il est
défini en fonction de lui-même.
 Exemple: x0
= 1, xn
= x*xn-1
si n≥1
Fonction fact(x : entier, n : entier):entier
Variable Résultat : entier;
Début
Si(n=0) alors
Résultat =1;
Sinon
Résultat = x*fact(x,n-1);
Fsi
Renvoyer Résultat;
Fin
24/02/2023 104

MÉTHODES DE TRI
ÉLÉMENTAIRES
•Définition
•Tri par sélection
•Tri par bulles
•Tri par insertion
24/02/2023 105

Définition
 « trier » signifie « répartir en plusieurs
classes selon certains critères ».
 De manière plus restrictive, le terme de
« tri » en algorithmique est très souvent
attaché au processus de classement d'un
ensemble d'éléments dans un ordre donné.
 Par exemple, trier N entiers dans l'ordre
croissant, ou N noms dans l'ordre
alphabétique.
 Tout ensemble muni d'un ordre total peut
fournir une suite d'éléments à trier.
24/02/2023 106

Tri par sélection
 Tri par sélection est l’un des algorithmes
de tri les plus simple, elle procède à la
sélection successive de l’élément
minimal parmi ceux restant. Il fonctionne
de la manière suivante :
◦ On commence par rechercher l’élément de
plus petite valeur du tableau pour l’échanger
avec celui en première position.
◦ On recherche ensuite l’élément ayant la
deuxième plus petite valeur pour l’échanger
avec celui en deuxième position, et l’on
continue ainsi jusqu’à ce que le tableau soit
24/02/2023 107

Tri par sélection(suite)
 Le sous-algorithme suivant est une implantation de ce processus.
Pour tout i entre 1 et N-1, on échange T[i] avec l’élément de valeur
minimal parmi T[i]….T[N] :
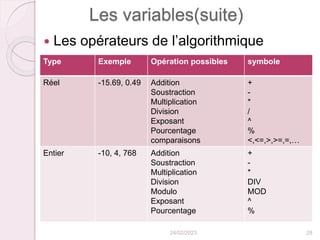
Pocédure TriSelection(T: 1…N: entier; N: entier)
Var i, j, min, q:entier;
Début
pour i de 1 jusqu’à N faire
min=i;
pour j de i+1 jusqu’à N faire
Si(T[j]<T[min]) alors
min=j;
Fsi
Fpour
q=T[min]; T[min]=T[i]; T[i]=q;
Fpour
Finprocédure
24/02/2023 108
A mesure que l’indice i progresse
vers la droite du fichier, les
éléments situés à sa gauche ont
pris leur position définitive et le
tableau est trié lorsque l’indice i
atteint l’extrémité droite

Tri par sélection(suite)
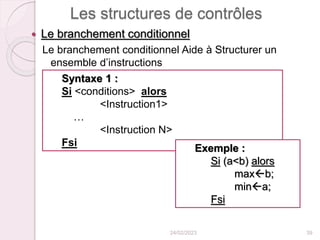
 Il est facile de compter le nombre d'opérations. Quel que
soit l'ordre du tableau initial, le nombre de comparaisons
reste le même, ainsi que le nombre d'échanges. À
chaque itération, on considère l'élément tab[i] et on le
compare successivement à tab[i+1], ..., tab[N]. On fait
donc N-i comparaisons.
 Le nombre total de comparaisons est donc de :
 et il y a (N-1) échanges.
 En ce qui concerne sa complexité, on dit que le tri par
sélection est en O (N2), à la fois dans le meilleur des cas,
en moyenne et dans le pire des cas, c'est-à-dire que son
temps d'exécution est de l'ordre du carré du nombre
d'éléments à trier.
24/02/2023 109

Tri par bulle
 Le « tri bulle » est une variante du tri par sélection.
Il consiste à parcourir le tableau tab en permutant
toute paire d'éléments consécutifs (tab[k],tab[k+1])
non ordonnés - ce qui est un échange et nécessite
donc encore une variable intermédiaire de type
entier. Après le premier parcours, le plus grand
élément se retrouve dans la dernière case du
tableau, en tab[N], et il reste donc à appliquer la
même procédure sur le tableau composé des
éléments tab[1], ..., tab[N-1]. Le nom de ce tri
provient du déplacement des « bulles » les plus
grandes vers la droite.
24/02/2023 110

Tri par bulle(suite)
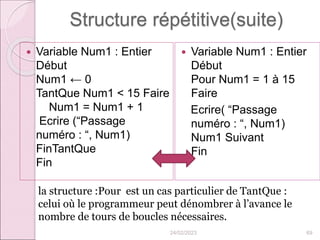
/* Procédure de tri bulle */
procedure triBulle(entier[] tab)
entier i, k; entier tmp;
pour (i de N à 2 en décrémentant de 1) faire
pour (k de 1 à i-1 en incrémentant de 1) faire
si (tab[k] > tab[k+1]) alors
tmp <- tab[k];
tab[k] <- tab[k+1];
tab[k+1] <- tmp;
fin si
fin pour
fin pour
fin procedure 24/02/2023 111

Tri par bulle(suite)
 Le nombre de comparaisons dans la procédure de tri bulle
est le même que pour le tri par sélection :
 Le nombre d'échanges quant à lui dépend de l'ordre des
éléments dans le tableau :
◦ dans le meilleur des cas, le tableau initial est trié et il n'y a pas
d'échange à faire ;
◦ en moyenne, on montre que le nombre d'échanges est de :
 dans le pire des cas, les entiers du tableau sont initialement
donnés dans l'ordre décroissant. Dans ce cas, on effectue
l'échange à chaque comparaison, c'est-à-dire que le nombre
d'échanges est alors de :
 Quoi qu'il en soit, la complexité du tri bulle reste en O (N2),
c'est-à-dire du même ordre de grandeur que le carré du
nombre d'éléments.
24/02/2023 112

Tri par insertion
 Cette méthode de tri est très différente de la méthode de tri
par sélection et s'apparente à celle utilisée pour trier ses
cartes dans un jeu : on prend une carte, tab[1], puis la
deuxième, tab[2], que l'on place en fonction de la première,
ensuite la troisième tab[3] que l'on insère à sa place en
fonction des deux premières et ainsi de suite. Le principe
général est donc de considérer que les (i-1) premières
cartes, tab[1],..., tab[i-1] sont triées et de placer la ie carte,
tab[i], à sa place parmi les (i-1) déjà triées, et ce jusqu'à ce
que i = N.
 Pour placer tab[i], on utilise une variable intermédiaire tmp
pour conserver sa valeur qu'on compare successivement à
chaque élément tab[i-1],tab[i-2],... qu'on déplace vers la
droite tant que sa valeur est supérieure à celle de tmp. On
affecte alors à l'emplacement dans le tableau laissé libre
par ce décalage la valeur de tmp.
24/02/2023 113

Tri par insertion(suite)
/* Procédure de tri par insertion */
procedure triInsertion(entier[] tab)
entier i, k,tmp;
pour (i de 2 à N en incrémentant de 1) faire
tmp <- tab[i];
k <- i;
tant que (k > 1 et tab[k - 1] > tmp) faire
tab[k] <- tab[k - 1]; k <- k - 1;
fin tant que tab[k] <- tmp;
fin pour
fin procedure 24/02/2023 114

Tri par insertion(suite)
 La comparaison avec les deux algorithmes précédents
montre que la complexité du tri par insertion est plus
fortement dépendante de l'ordre du tableau initial.
Nous comptons ici le nombre de comparaisons (qui
est le nombre de décalages à un près) :
◦ dans le meilleur des cas, le tableau initial est trié et on
effectue alors une comparaison à chaque insertion, on
effectue donc N-1 comparaisons ;
◦ en moyenne, on montre que le nombre de comparaisons est
de :
24/02/2023 115

coursalgorithmique9-10.ppt

Contenu connexe

Tendances

Similaire à coursalgorithmique9-10.ppt

Dernier

coursalgorithmique9-10.ppt