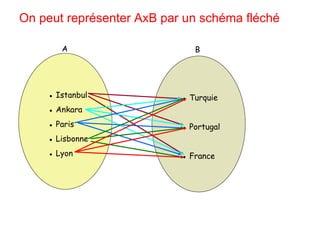
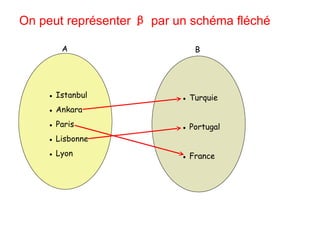
Le document explore les relations d'ensembles, en présentant des exemples de produits cartésiens, de sous-ensembles, et en définissant des propriétés telles que la réflexivité, la symétrie, et la transitivité des relations. Il illustre comment déterminer si une relation est réflexive ou symétrique à l'aide d'exemples concrets. La discussion se concentre également sur les conditions nécessaires pour qu'une relation soit antisymétrique et transitive.

1. Soit deux ensembles A et B A={ Istanbul, Ankara, Paris, Lisbonne, Lyon } B={ Turquie, Portugal, France } AxB= { ( Istanbul , Turquie ), ( Istanbul , Portugal ), ( Istanbul , France ),( Ankara , Turquie ), ( Ankara , Portugal ) ,…} n(AxB)=n(A).n(B)=5.3=15 Activité

2. On peut représenter AxB par un schéma fléché ● Istanbul ● Ankara ● Paris ● Lisbonne ● Lyon ● Turquie ● Portugal ● France A B

3. Relation A={ Istanbul, Ankara, Paris, Lisbonne, Lyon } B={ Turquie, Portugal, France } Ecrire l’ensemble des couples (x,y) tels que x est élément de A y est élément de B x est la capitale de y et noté cet ensemble par β β ={( Ankara , Turquie ),( Paris , France ),( Lisbonne , Portugal )} β ={(x,y): x est la capitale de y , x ∈A et y ∈B }

4. Question : Quelle est la relation entre les ensembles AxB et β ? AxB= { ( Istanbul , Turquie ), ( Istanbul , Portugal ), ( Istanbul , France ),( Ankara , Turquie ), ( Ankara , Portugal ) ,…} β ={( Ankara , Turquie ),( Paris , France ),( Lisbonne , Portugal )} Réponse : β est un sous ensemble de AxB

5. On peut représenter β par un schéma fléché ● Istanbul ● Ankara ● Paris ● Lisbonne ● Lyon A ● Turquie ● Portugal ● France B

6. Relation Chaque sous ensemble de AxB est une relation de A vers B. Définition: A≠ø et B≠ø

7. Exemple A={2,3,5} B={2,9,12,15} β ={(x,y): x Є A, y Є B et « x divise y » } β ={ (2,2),(2,12),(3,9),(3,12),(3,15),(5,15)}

8. Exemple A={3,5,15,22} β ={(x,y): x, y Є A et « x est un multiple de y » } β ={ (3,3),(5,5),(15,15),(22,22),(15,3),(15,5)}

9. Exemple A={0,1,2} B={-1,1,3,5,6} Parmi les relations suivantes, déterminer celles qui sont définies de A vers B. β ={ (1,3),(0,-1),(3,5) } β ={ (1,5),(2,6),(3,-1) } β ={ (1,3),(1,5),(0,2),(2,6) } β ={ (0,-1),(0,1),(0,5),(0,6),(0,3) } β ={ (2,3)} β ={ }

10. PROPRIETES D’UNE RELATION

11. Réflexivité : On dit qu’une relation β est réflexive si et seulement si pour tout x de A, (x,x) Є β

12. Exemple 1 A={a,b,c} β = { , , , , } (a,a) (b,b) (c,c) (a,b) (c,a) β est-elle réflexive ? Oui, car (a,a) є β , (b,b) є β , (c,c) є β

13. Exemple 2: A= { a , b , c } β = { } (a,a) (a,b) (b,a) (c,c) (c,b) (a,c) β est-elle réflexive ? Non , car (a,a) є β , (c,c) є β , Mais (b,b) n’est pas élément de β

14. EXEMPLE 3 A= { 1, 2, 3, 4 } a) β = { (1,1), (2,2) , (3,3), (4,4) } Elle est réflexive b) β = { (1,1), (1,2) , (3,3), (4,4), (4,2) } Elle n’est pas réflexive Car (2,2) n’est pas un élément de β c) β ={ (1,1),(2,2) ,(2,3),(3,4),(1,4),(3,3), (4,4) } Elle est réflexive

15. Symétrie On dit qu’une relation β est symétrique si et seulement si pour tout (x,y) de β , (y,x) Є β

16. EXEMPLE 1 : Exemple 1: A= { a, b, c } β = { , , , , , } (a,a) (a,b) (b,a) (b,c) (c,b) (c,c) β est-elle symétrique ? elle est symétrique OUI

17. EXEMPLE 2 : A= { a, b, c } β = { , , , , , , } (a,a) (a,b) (b,a) (a,c) (b,c) (c,b) (c,c) β est-elle symétrique ? Elle n’est pas symétrique Car (a,c) est un élément de β Mais (c,a) n’est pas un élément de β

18. EXEMPLE 3 : A ={ 1, 2, 3, 4 } a) β = { (1,2) , (2,1) , (3,4) , (4,1) , (4,3) , (1,4), } SYMETRIQUE b) β = { (1,2) , (3,4) , (2,3) , (3,2) , (2,1) , (4,4) } PAS SYMETRIQUE c) β = { (1,4) , (2,2) , (3,2) , (4,4) , (4,1) } PAS SYMETRIQUE d) β = { (1,1) , (2,2) , (3,3) , (4,4) } SYMETRIQUE

19. Antisymétrie On dit qu’une relation β est antisymétrique si et seulement si pour tout (x,y) de β , x≠y (y,x) n’est pas un élément de β

20. EXEMPLE 1 : A= { 1, 2, 3 } β = { , , , , , } β est-elle antisymétrique ? OUI (1,1) (1,2) (1,3) (2,2) (2,3) (3,3)

21. EXEMPLE 2 : A= { 1, 2, 3 ,4 } β = { , , , , , , } β est-elle antisymétrique ? NON (1,2) (2,3) (4,4) (3,3) (1,1) (3,2) (1,4)

22. Transitivité On dit que la relation β est transitive.

23. Exemple A={a,b,c,d} β ={ (a,a) , (b,c) , (c,c) , (c,d) , (b,d) } β est-elle transitive ? Oui

24. Exemple A={a,b,c} β ={ (a,a) , (b,b) , (c,c) , (a,b) , (b,c) , (c,b) } β est-elle transitive ? Non car (a,b) є β et (b,c) є β , mais (a,c) n’est pas élément de β

25. Exemple A={a,b,c} et β est une relation qui est définie dans A. Étudier les propriétés de β a) β ={ (a,a) , (b,b) , (c,c) , (b,c) , (c,b) } Elle est réflexive Elle est symétrique Elle est transitive b) β ={ (a,a) , (a,b) , (b,c) , (c,b) } Elle n’est pas réflexive Elle n’est pas symétrique Elle n’est pas antisymétrique Elle n’est pas transitive c) β ={ (a,b) , (b,c) , (a,c) , (b,a) , (a,a) } Elle n’est pas réflexive Elle n’est pas symétrique Elle n’est pas antisymétrique Elle n’est pas transitive