Le document aborde les modèles de prévision, notamment à travers des concepts de régression linéaire simple et multiple, incluant des tests de significativité comme le test de Student. Il présente également des analyses de variance et des mesures de performance des modèles, comme le coefficient de détermination R². Enfin, il discute des tests multiples et des énoncés d'hypothèses pour évaluer la pertinence des coefficients dans un modèle de régression.

1. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Mod`les de pr´vision
e e
Partie 1 - r´gression
e
Arthur Charpentier
charpentier.arthur@uqam.ca
http ://freakonometrics.blog.free.fr/
Automne 2012
1

2. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Plan du cours
• Motivation et introduction aux mod`les de r´gression
e e
• Le mod`le lin´aire simple
e e
◦ R´sultats g´n´raux
e e e
◦ Approche matricielle
• Le mod`le lin´aire multiple
e e
◦ R´sultats g´n´raux
e e e
◦ Tests, choix de mod`le, diagnostique
e
• Aller plus loin
◦ Les mod`les non lin´aires param´triques
e e e
◦ Les mod`les non lin´aires nonparam´triques
e e e
2

3. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Petit rappel sur la significativit´, test de H0 : βj = 0
e
Les r´sultats pr´c´dants permettent de proposer un test simple de
e e e
H0 : βj = 0 contre l’hypoth`se H1 : βj = 0.
e
La statistique de test
βj
Tj = ∼ St(n − k) sous H0 .
V ar(βj )
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -17.5791 6.7584 -2.601 0.0123 *
speed 3.9324 0.4155 9.464 1.49e-12 ***
3

4. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Les deux lectures possibles d’un test
• donner la region de rejet, de la forme [±T1−α/2 ], avec un seuil α fix´
e
arbitrairement ( par d´
faut 95%)
• donner le seuil α tel que la r´gion de rejet soit [±t] (la plus petite region de
e
rejet ` laquelle appartienne la statistique observ´e), i.e. la probabilit´ que de
a e e
rejeter H0 si H0 ´tait vraie.
e
Dans ce dernier cas, on parle de p-value, p = P(rejeter H0 |H0 vraie) : si p est
faible, on rejette H0 , car il y a peu de chances qu’H0 soit vraie.
4

5. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Lecture du test de Student
Region de rejet du test de Student
0.4
REJET ACCEPTATION REJET
0.3
DE H0 DE H0 DE H0
0.2
0.1
Aire totale = 5%
0.0
−6 −4 −2 0 2 4 6
5

6. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Lecture du test de Student
p−value associée à un test de Student
0.4
0.3
0.2
0.1
Aire totale = 1,23%
0.0
−6 −4 −2 0 2 4 6
6

7. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Analyse d’une sortie de r´gression
e
Des tests de student de H0 : βi = 0, contre H1 : βi = 0 sont propos´s, avec
e
β0 − β0 −17.5791 − 0
t0 = = = −2.601 sousH0
6.7584
V ar(β0 )
β1 − β1 3.9324 − 0
t1 = = = 9.464 sousH0
0.4155
V ar(β0 )
Ces valeurs sont ` comparer avec le quantile de Student ` 95% (` 49 degr´s de
a a a e
libert´).
e
Une alternative est d’utiliser la p-value, i.e. si Z ∼ St(49),
p0 = P(|Z| > t0 ) = 0.0123 et p1 = P(|Z| > t1 ) = 1.49 × 10−12 .
7

8. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
La p value est alors donn´e par
e
> 2*(1-pt(abs(REG$coefficients[1]/summary(REG)$coefficients[1,2]), df=n-2))
(Intercept)
0.01231882
σ = 15.38, i.e. summary(reg)$sigma
> confint(reg)
2.5 % 97.5 %
(Intercept) -31.167850 -3.990340
speed 3.096964 4.767853
Pour la constante, par exemple, l’intervalle de confiance est donn´ par
e
> REG$coefficients[1]+qt(c(.025,.975),n-2)* summary(REG)$coefficients[1,2]
[1] -31.16785 -3.99034
La matrice de variance-covariance des coefficients, Var(β) est ici
8

9. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
> vcov(reg)
(Intercept) speed
(Intercept) 45.676514 -2.6588234
speed -2.658823 0.1726509
9

10. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Introduction aux tests multiples, e.g. H0 : β1 = · · · = βj = 0
On a vu comment tester H0 : β2 = 0 et H0 : β3 = 0, mais ces deux tests peuvent
ˆtre valid´, sans pour autant avoir H0 : β2 = β3 = 0.
e e
> US=read.table("http://freakonometrics.free.fr/US.txt",
+ header=TRUE,sep=";")
> US$Density=US$Population/US$Area
> model1 = lm(Murder ~ Income + HS.Grad + Frost +
+ Population + Illiteracy + Life.Exp +
+ Area + Density, data=US)
> summary(model1)
Call:
lm(formula = Murder ~ Income + HS.Grad + Frost + Population +
Illiteracy + Life.Exp + Area + Density, data = US)
Residuals:
Min 1Q Median 3Q Max
-3.10973 -0.92363 -0.07636 0.74884 2.92362
10

11. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.121e+02 1.684e+01 6.657 5.04e-08 ***
Income 1.018e-03 6.642e-04 1.532 0.133084
HS.Grad 1.318e-02 5.315e-02 0.248 0.805412
Frost -7.301e-03 7.074e-03 -1.032 0.308040
Population 2.180e-04 6.051e-05 3.602 0.000845 ***
Illiteracy 2.208e+00 8.184e-01 2.699 0.010068 *
Life.Exp -1.579e+00 2.374e-01 -6.652 5.12e-08 ***
Area -9.413e-07 4.228e-06 -0.223 0.824911
Density -4.369e+00 1.499e+00 -2.915 0.005740 **
---
Signif. codes: 0 *** 0.001 ** 0.01 * 0.05 . 0.1 1
Residual standard error: 1.608 on 41 degrees of freedom
Multiple R-squared: 0.8412, Adjusted R-squared: 0.8102
F-statistic: 27.14 on 8 and 41 DF, p-value: 4.813e-14
Sur cette exemple, on valide les tests H0 : β1 = 0, H0 : β2 = 0 et H0 : β3 = 0.
Mais peut-on valider H0 : β1 = β2 = β3 = 0 ?
11

12. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Ce test peut s’´crire de mani`re tr`s g´n´rale H0 : Rβ = q (contre H1 : Rβ = q)
e e e e e
avec ici  
β0
 
β 
 1
    
0 1 0 0 0 · · · 0  β2    0
    
0 0 1 0 0 · · · 0 β3  = 0
    
 
0 0 0 1 0 · · · 0  β4    0
.
.
R . 0
βk
β
La strat´gie est de comparer deux mod`les : le mod`le non-contraint (sous H1 ),
e e e
β = argmin{(Y − Xβ) (Y − Xβ), β ∈ Rk+1 }
12

13. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
et le mod`le non-contraint (sous H1 ),
e
β = argmin{(Y − Xβ) (Y − Xβ), β ∈ Rk+1 , Rβ = q}
Pour le premier mod`le, on cherche ` minimiser
e a
h(β) = (Y − Xβ) (Y − Xβ)
et dans le second mod`le, c’est de la minimisation sous-contrainte. On optimise le
e
Lagrangien,
(β, λ) = (Y − Xβ) (Y − Xβ) + λ(Rβ − q)
Dans ce cas, les conditions du premier ordre sont
∂ (β, λ)
= 2X (Y − Xβ) + R λ = 0
∂β
et
∂ (β, λ)
= Rβ − q = 0,
∂λ
13

14. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
pour β = β . On a finallement un syst`me de deux (syst`mes d’) ´quations
e e e
    
XX R β XY
   =  
R 0 λ q
Comme β = (X X)−1 X Y , on peut ´crire
e
β = β − C[Rβ − q]
o`
u
C = (X X)−1 R [R(X X)−1 R ]−1 .
Si on pose ε = Y − X β et ε = Y − X β, alors
ε ε − ε ε = [Rβ − q] (R(X X)−1 R )[Rβ − q]
Or d’apr`s la seconde condition du premier ordre, Rβ = q. Donc sous H0 , la
e
statistique de test est
ε ε −εε n−k
F = ·
dim(q) εε
14

15. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
qui doit suivre une loi de Fisher, F(dim(q), n − k).
> (EE=sum(residuals(model1)^2))
[1] 106.0532
> model2 = lm(Murder ~
+ Population + Illiteracy + Life.Exp +
+ Area + Density, data=US)
> (EEc=sum(residuals(model2)^2))
[1] 119.6924
> (F=(EEc-EE)/3*(nrow(US)-9)/(EE))
[1] 1.757643
> 1-pf(F,3,nrow(US)-9)
[1] 0.170363
Pour savoir si on rejette, ou si on accepte H0 , on calcule la p-value,
> 1-pf(F,3,nrow(US)-9)
[1] 0.170363
i.e. on peut accepter ici H0 (les trois coefficients sont nuls simultan´ment).
e
Cette analyse de variance peut se faire via
15

16. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
> library(car)
> linearHypothesis(model1,
+ c("Income","HS.Grad","Frost"),c(0,0,0))
Linear hypothesis test
Hypothesis:
Income = 0
HS.Grad = 0
Frost = 0
Model 1: restricted model
Model 2: Murder ~ Income + HS.Grad + Frost +
Population + Illiteracy + Life.Exp + Area + Density
Res.Df RSS Df Sum of Sq F Pr(>F)
1 44 119.69
2 41 106.05 3 13.639 1.7576 0.1704
16

17. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Diagnostique et r´gression, le R2
e
Le coefficient de d´termination R2 d´fini ` partir le rapport entre la variance des
e e a
r´sidus et la variance de Y ,
e
2 Variance non expliqu´e
e Variance expliqu´e
e
R =1− = .
Variance totale Variance totale
ou pour la version empirique
n 2
Yi − Yi
somme des carr´s des r´sidus
e e i=1
R2 = 1 − =1− n
somme des carr´s de la r´gression
e e 2
Yi − Y
i=1
17

18. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Diagnostique et r´gression, le R2
e
On utilise pour cela la formule de d´composition de la variance
e
V ar(Y ) = V ar[E(Y |X)] + E[V ar(Y |X)] .
variance totale variance expliqu´e par X
e variance r´isudelle
e
On notera que cette grandeur est un estimateur bais´ du vrai R2 ,
e
2 k−1 2 1
E(R ) = R + [1 − R2 ] + O
n−1 n2
2
Le coefficient d’ajustement est R2 = 0.6511 et R = 0.6438.
> summary(reg)$r.squared
[1] 0.6510794
Le calcul se fait de la mani`re suivante
e
> 1-deviance(REG)/sum((Y-mean(Y))^2)
[1] 0.6510794
18

19. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Afin de prendre en compte le nombre de param`tre, et de corriger du biais, on
e
peut utiliser le R2 ajust´,
e
2 n−1 (n − 1)R2 − (k − 1)
R = 1 − (1 − R2 ) =
n − (k − 1) − 1 n−k−2
o` (k − 1) est le nombre de variables explicatives (sans la constante). Notons que
u
2
ce R peut ˆtre n´gatif.
e e
Remarque En rajoutant des variables explicatives, on ne peut que augmenter le
R2 , mais si ces derni`res sont peu corr´l´es avec Y .
e ee
Remarque Dans un mod`le sans constante, le R2 n’a plus aucun sens. En fait,
e
sans constante, rien ne garantit que le plan de r´gression passe par le centre de
e
gravit´ du nuage, (x, y). Et donc la somme des r´sidus n’est alors pas forc´ment
e e e
nulle. La formule de d´composition de la variance n’est alors plus valide.
e
19

20. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
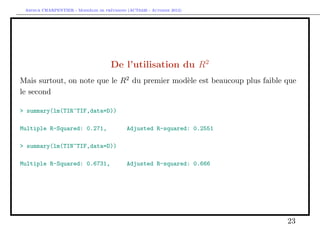
De l’utilisation du R2
Consid´rons une r´gression lin´aire
e e e
T INt = β0 + β1 T IFt + εt ,
o` T IN d´signe le taux d’int´rˆ nomial, T IF le taux d’inflation et T IR le taux
u e et
d’int´rˆt r´el, i.e. T IN = T IR + T IF . Au lieu de mod´liser le taux d’int´rˆt
ee e e ee
nominal en fonction de l’inflation, supposons que l’on cherche ` mod´liser le taux
a e
d’int´rˆt r´el,
ee e
T IRt = α0 + α1 T IFt + ηt .
Notons que de la premi`re ´quation T INt = β0 + β1 T IFt + εt = T IRt + T IFt , on
e e
en d´duit
e
T IRt = β0 + [β1 − 1] T IFt + εt ,
=α0 =β0 =ηt
autrement dit les deux ´quations sont ´quivalentes.
e e
20

21. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Pourtant
2 V ar(η) V ar(η) V ar(η) 2
Rnominal =1− =1− ≥1− = Rr´el
e
V ar(T IN ) V ar(T IR + T IF ) V ar(T IR)
aussi, on peut artificiellement augmenter un R2 , tout en ´tudiant un mod`le
e e
rigoureusement ´quivalent.
e
15
10
5
0
1960 1970 1980 1990 2000
21

22. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
De l’utilisation du R2
Les sorties montrent que les deux sorties sont effectivement ´quivalence entre les
e
deux mod`les
e
> summary(lm(TIR~TIF,data=D))
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4.65040 0.44301 10.497 8.5e-14 ***
TIF -0.29817 0.07211 -4.135 0.000149 ***
> summary(lm(TIN~TIF,data=D))
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4.65040 0.44301 10.497 8.50e-14 ***
TIF 0.70183 0.07211 9.733 9.55e-13 ***
22

23. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
De l’utilisation du R2
Mais surtout, on note que le R2 du premier mod`le est beaucoup plus faible que
e
le second
> summary(lm(TIR~TIF,data=D))
Multiple R-Squared: 0.271, Adjusted R-squared: 0.2551
> summary(lm(TIN~TIF,data=D))
Multiple R-Squared: 0.6731, Adjusted R-squared: 0.666
23

24. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Diagnostique dans le mod`le lin´aire
e e
La fonction plot(REG) produit 6 graphiques de diagnostique
1. r´sidus contre valeurs estim´es, (Yi , εi ) (plot of residuals against fitted values)
e e
2. (Yi , |εi |) (Scale-Location plot),
3. un graphique quantile-quantile des r´sidus (Normal Q-Q plot),
e
4. un graphique de distances de Cook (plot of Cook’s distances versus row
labels),
5. un graphique de leverage (plot of residuals against leverages)
6. (plot of Cook’s distances against leverage/(1-leverage))
Remarque dans la plupart des graphiques, on utilise les r´sidus standardis´s,
e e
i.e. ε/σ, centr´s et de variance unitaire.
e
24

25. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Diagnostique dans le mod`le lin´aire
e e
> plot(predict(REG),residuals(REG))
> abline(h=0,lty=2,col="grey")
> lines(lowess(predict(REG),residuals(REG)),col="red")
>
Residuals vs Fitted
q q
40
q 23 49 q
40
q
q 35
q q
20
q q
20
residuals(REG)
q
q q
q
Residuals
q q q q q q q
q q q q
q
q q q q q q
q q q q q q
q q q q
0
q q
0
q q
q q q q
q q q q q
q q q
q q q q q
q q q q q
q q
q q q q q q
q q q
q q q
q q q
q q
−20
q q q
q q q
−20
q
q q
q
q
0 20 40 60 80 0 20 40 60 80
Fitted values predict(REG)
lm(dist ~ speed)
25

26. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Diagnostique dans le mod`le lin´aire
e e
> s=summary(REG)$sigma
> plot(qnorm((1:50)/51),sort(residuals(REG))/s)
> abline(a=0,b=1,lty=2,col="grey")
> lines(lowess(qnorm((1:50)/51),sort(residuals(REG))/s),col="red")
Normal Q−Q
q q
3
49 q
q 23
q
2
q 35
2
q q
Standardized residuals
sort(residuals(REG))/s
q q
q
1
q
qq qqqqq
1
q
qqqqq
q
qqq
qq
qq
qq
q
qq
q
qq
qq
0
qq
q qq
0
qq qq
qq qq
qq
qq q
qq qqq
qq
q qqq
qq
qq qqq
qqq qq
qq
−1
−1
qq
qq q
q q
q
q q q q
q q
−2
−2
−2 −1 0 1 2 −2 −1 0 1 2
Theoretical Quantiles qnorm((1:50)/51)
lm(dist ~ speed)
26

27. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Diagnostique dans le mod`le lin´aire
e e
> plot(predict(REG),sqrt(abs(residuals(REG))/s))
> abline(h=mean(sqrt(abs(residuals(REG))/s)),lty=2,col="grey")
> lines(lowess(predict(REG),sqrt(abs(residuals(REG))/s)),col="red")
>
Scale−Location
49 q q q
q 23
1.5
1.5
q 35 q
q q
sqrt(abs(residuals(REG))/s)
q
Standardized residuals
q
q q q q
q q q
q q q
1.0
q q q q
q
1.0
q q q q q
q q q q q
q q q
q q q
q q q q
q q q q
q q q q
q
q q q
q q q
q
q q
q q q
q q
q q
0.5
q q q q q
q q q
q
q
0.5
q q
q q q
q q q q q
q q
q
q q q
q
0.0
q
0 20 40 60 80 0 20 40 60 80
Fitted values predict(REG)
lm(dist ~ speed)
27

28. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Diagnostique dans le mod`le lin´aire
e e
> library(car)
> plot(cooks.distance(REG))
>
>
Cook's distance
0.35
q
49
0.30
0.3
0.25
cooks.distance(REG)
Cook's distance
0.20
0.2
0.15
0.10
0.1
23 q
39 q
0.05
q q
q q
q
q q q
q q
q
q qqq q q
0.00
q q q q qq q q q q q q qq q q q q qq qq q
0.0
q qq q qq q
0 10 20 30 40 50 0 10 20 30 40 50
Obs. number Index
lm(dist ~ speed)
28

29. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Diagnostique dans le mod`le lin´aire
e e
> X=cbind(1,cars$speed); L=diag(X%*%solve(t(X)%*%X)%*%t(X))
> plot(L,residuals(REG)/s)
> abline(h=0,lty=2,col="grey")
> lines(lowess(L,residuals(REG)/s),col="red")
Residuals vs Leverage
q q
3
49 q
q 23
0.5
q
2
q
2
q q
Standardized residuals
q q
residuals(REG)/s
q
1
q q
q
1
q q q q q
q q q q q q
q
q q q q q q
q qq q q qq
qq q
qq
0
0
q q q
q q q
q q q q
q qq
q q q q q qq
q q qq q
q q
q q q q q q
q q
q q q
−1
q q q
q q
−1
q q q
q q q
q
q q
q 39
−2
Cook's distance q
−2
0.00 0.02 0.04 0.06 0.08 0.10 0.02 0.04 0.06 0.08 0.10
Leverage L
lm(dist ~ speed)
29

30. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Diagnostique dans le mod`le lin´aire
e e
> plot(L,cooks.distance(REG))
> lines(lowess(L,cooks.distance(REG)),col="red")
>
>
Cook's distance vs Leverage
0.35
0.35
3 2.5 2 q
49 q
0.30
0.30
1.5
0.25
0.25
cooks.distance(REG)
Cook's distance
0.20
0.20
0.15
0.15
1
0.10
0.10
q 23 q
q 39 q
0.05
0.05
q q q q
q q q
q q q
q q q
0.5 q
q q q
qq q
q q
qqq q qq q qq q q q
0.00
0.00
qqq q q
q q q
q qq q q q q q
qq q q qq
q
q qq q q
q q q q
q q
q q q q 0 qq q q
q q q q q q q
0.02 0.04 0.06 0.08 0.1 0.02 0.04 0.06 0.08 0.10
Leverage L
lm(dist ~ speed)
30

31. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Les points atypiques et influents
La notion d’outliers ou de points ab´rants.
e
La distance de Cook mesure l’impact sur la r´gression de l’absence d’une
e
observation. Aussi
n ˆ ˆ
j=1 (Yj − Yj(i) )2
Ci =
p · M SE
ou encore,
ε2
i hii
Ci =
p · M SE (1 − hii )2
−1
o` hi,i est l´l´ment diagonale de la matrice H = X (X X) X (que l’on notera
u ee
parfois hi ). Les hi = [X(X X)−1 X]i,i = Hi,i sont appel´s (leverage).
e
31

32. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Le vecteur des leverages h = (h1 , · · · , hn ) est obtenu ais´ment sous R,
e
> diag(X%*%solve(t(X)%*%X)%*%t(X))[1:6]
[1] 0.11486131 0.11486131 0.07150365 0.07150365 0.05997080 0.04989781
> influence(REG)[1:6]
$hat
1 2 3 4 5 6
0.11486131 0.11486131 0.07150365 0.07150365 0.05997080 0.04989781
Les hypoth`ses sont que E(εi ) = 0 et V ar(εi ) = σ 2 . En r´alit´, E(εi ) = 0 mais
e e e
V ar(εi ) = [I − H]i,i σ 2 = σ 2
Notons que puisque Y = HY + ε,
ε = Y − Y = [I − H]Y = [I − H](Xβ + ε) = [I − H]ε,
et donc V ar(ε) = V ar([I − H]ε) = [I − H]σ 2 . Aussi, V ar(εi ) = [1 − hi ]σ 2 .
Les r´sidus Studentis´s sont les
e e
ε
εi = √ .
σ 1 − hi
32

33. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Notons que Var(εi ) = 1.
> diag(X%*%solve(t(X)%*%X)%*%t(X))
> rstudent(REG)[1:6]
1 2 3 4 5 6
0.26345000 0.81607841 -0.39781154 0.81035256 0.14070334 -0.51716052
> mean(rstudent(REG))
[1] 0.01347908
> sd(rstudent(REG))
[1] 1.045681
Sur la matrice de leverage (matrice de projection orthogonale), notons que
Yi = HY = hi,i Yi + hi,j Yj .
j=i
Aussi, hi,i est le poids accord´ ` Yi pour sa propre pr´diction.
ea e
• si hi,i = 1, Yi est uniquement d´termin´ par Yi (hi,j = 0 pour j = i),
e e
• si hi,i = 0, Yi est n’est nullement influenc´ par Yi .
e
33

34. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
On parelera de point levier i si hi,i est trop grand, i.e.
• si hi,i > 2k/n, d’apr`s Hoaglin & Welsch (1978),
e
• si hi,i > 3k/n pour k > 6 et n − k > 12, d’apr`s Welleman & Welsch (1981),
e
• si hi,i > 1/2, d’apr`s Huber (1981).
e
Cette m´thode permet de d´tecter des points atypiques, ou plutˆts des points
e e o
influents.
Afin de mesurer l’impact d’une observation sur la r´gression, il peut aussi ˆtre
e e
utile de regarder les r´sultats de la r´gression si l’on supprime une des
e e
observations.
Apr`s suppression de la i`me observation, les estimateurs des moindres carr´s
e e e
s’´crivent
e
εi
β (i) = β − (X X)−1 X i ·
1 − hi,i
2 1 ε2
i
2
σ(i) = (n − k)σ
n−k−1 1 − hi,i
34

35. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
> i=25
> REGi=lm(dist~speed,data=cars[-i,])
> plot(cars); points(cars[i,],col="red",pch=19)
> abline(REG,lty=2); abline(REGi,lwd=2,col="red")
120
q
100
q
q
q q
80
q
q
q
q
q
q
dist
60
q
q q
q q
q
q
q
q q
q
40
q q
q q
q q
q q q
q q
q q q q
q
q
20
q q
q q
q
q
q q
q
q
0
5 10 15 20 25
speed
35

36. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
> i=23
> REGi=lm(dist~speed,data=cars[-i,])
> plot(cars); points(cars[i,],col="red",pch=19)
> abline(REG,lty=2); abline(REGi,lwd=2,col="red")
120
q
100
q
q
q q
80
q
q
q
q
q
q
dist
60
q
q q
q q
q
q
q
q q
q
40
q q
q q
q q
q q q
q q
q q q q
q
q
20
q q
q q
q
q
q q
q
q
0
5 10 15 20 25
speed
36

37. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
> i=49
> REGi=lm(dist~speed,data=cars[-i,])
> plot(cars); points(cars[i,],col="red",pch=19)
> abline(REG,lty=2); abline(REGi,lwd=2,col="red")
120
q
100
q
q
q q
80
q
q
q
q
q
q
dist
60
q
q q
q q
q
q
q
q q
q
40
q q
q q
q q
q q q
q q
q q q q
q
q
20
q q
q q
q
q
q q
q
q
0
5 10 15 20 25
speed
Remarque Beaucoup d’autres distances, bas´es sur la fonction d’influence, ont
e
´t´ propos´es
ee e
(β − β (i) ) X X(β − β (i) )
Cook :Ci =
kσ 2
37

38. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
|X i (β − β (i) )|
Welsh-Kuh :W Ki = 2
σ(i) hi,i
n−1
Welsh :Wi = W Ki
1 − hi,i
vraisemblance :LDi = 2 L(β, σ 2 ) − L β (i) , σ(i)
2
Remarque : les points aberrants ont des valeurs de Y aberrantes, mais on
pourrait aussi vouloir tester une ab´ration en X.
e
38

39. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Analyse graphique des r´sidus, example
e
Pour illustrer, consid´rons les d´penses dans les ´coles publiques, par ´tat (aux
e e e e
U.S.A.)
> library(sandwich)
> data(PublicSchools)
>
> tail(PublicSchools)
Expenditure Income
Virginia 356 7624
Washington 415 8450
Washington DC 428 10022
West Virginia 320 6456
Wisconsin NA 7597
Wyoming 500 9096
39

40. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Analyse graphique des r´sidus, example
e
> plot(PublicSchools$Income,PublicSchools$Expenditure)
> id=c(2,49)
> text(PublicSchools$Income[id],PublicSchools$Expenditure[id],
+ rownames(PublicSchools)[id],pos=1)
q q
800
Alaska
200
700
150
Dépenses écoles publiques
Résidus de la régression
q
100
600
q
q q
q
50
q q q
q
500
q q q
q q q q
q q q
q q
q q q
q q q
q q
0
q q q q
q q q q q q
q q q q q q qq
400
q
q q Washington DC q q q
q q q q
−50
qq q
q q qq
q q
q q q q q qq
qq q q q
q q qq q
q q
300
q
q
−100
q
qq qq
q q
q q q q
6000 7000 8000 9000 10000 11000 6000 7000 8000 9000 10000 11000
Revenu (par tête) Revenu
40

41. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Analyse graphique des r´sidus, example
e
Residuals vs Fitted Normal Q−Q
Alaska q Alaska q
4
200
3
Standardized residuals
q Utah
100
q
2
q q
Residuals
q
q
q q q
q q
q q
q
1
q q
q q q
q
q q qq
q
q qq
q q q qq
q
q q qq
qq
0
q q q
q q q q qq
qqq
q
q
0
q q q q
q q q
qq q qqq
qqq
qq qq
q
qq
q qq qqq
q q qq
−1
q
−100
q qq
q q
q
Nevadaq q
q Nevada
−2
q Washington DC
250 300 350 400 450 500 550 600 −2 −1 0 1 2
Fitted values Theoretical Quantiles
lm(Expenditure ~ Income) lm(Expenditure ~ Income)
41

42. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Analyse graphique des r´sidus, example
e
Scale−Location Cook's distance
2.5
2.0
Alaska q
Alaska
2.0
1.5
Standardized residuals
Washington DC q
q Nevada
q
Cook's distance
q
1.5
q
q
q
q q
q
qq
1.0
q
q q q
q
qq q
1.0
q
q
q q q q
q q
q
q q
q q q
q
q q
q qq
0.5
q q
0.5
q
q q
q
q Washington DC
q
Nevada
0.0
0.0
q
250 300 350 400 450 500 550 600 0 10 20 30 40 50
Fitted values Obs. number
lm(Expenditure ~ Income) lm(Expenditure ~ Income)
42

43. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Analyse graphique des r´sidus, example
e
Residuals vs Leverage Cook's distance vs Leverage
5 4 3
Alaska q
Alaska q
4
2.0
3
1
Standardized residuals
1.5
Cook's distance
2
q 0.5
q
q q
q
1
q q 2
qq
1.0
q
q qq q q q
q
q
q q q
q qq
0
q
q q
q q qq
q
q qq
q
qq qq
0.5
q
−1
q
q
q q
q
q Washington DC 1
q Nevada 0.5
−2
q Washington DC q Nevada
qq
0.0
Cook's distance q qq q qq
qq q q qqq q
qqqqq qq qq q
q q 0
1
0.00 0.05 0.10 0.15 0.20 0 0.05 0.1 0.15 0.2
Leverage Leverage
lm(Expenditure ~ Income) lm(Expenditure ~ Income)
43

44. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Analyse des r´sidus : quelles alternatives
e
Les hypoth`ses fondamentales sur les r´sidus sont
e e
• E(ε|X) = 0
• Var(ε|X) = σ 2 I
et ´ventuellement
e
• ε|X ∼ N (0, σ 2 I)
Un “mauvais mod`le est un mod`le pour lequel une de ces hypoth`ses n’est pas
e e e
valide
44

45. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Analyse graphique des r´sidus, suite
e
Graphique normal des r´sidus εi = Yi − X i β versus Xi
e
OOO OOO OOO OOO OOO OOO OOO OOO OOO OOO OOO OOO OOO
OOO OOO
q
4
2
q
q
qq q
q
q
qq
qq
2
q qq
q
q
1
q q qq
qq
q
Sample Quantiles
q q
q q q q q qq
q q q q
q qq
qq
qq
q q q q q q q q q q qq q q qqq
qq
qq
q
q q qq qq qq q q qqq
q q q qq q q qqq
qq
0
q q q q q
q q
q qq q qq
q
q q q q
qq
qq q qq qq
qq
0
q qq qqq qq
q q q q q q q qq
qq
q
q q
qq
q q q q q q qq
q
q q q q q
qq
q qq
q
q qq
qq
q
qq
q q q
qq
qqq
−2
q
q q
qq
−1
qq
qq
qq
qq
q
q
q
−4
q q
q
−2
q
−2 −1 0 1 2
Variable exogène (X) Theoretical Quantiles
45

46. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Analyse graphique des r´sidus, suite
e
Graphique des r´sidus εi = Yi − X i β versus Xi
e
Pr´sence de deux points atypiques, OOO OOO OOO OOO OOO OOO OOO
e
OOO OOO OOO
q
q
q
4
4
q
q
2
q q
2
q q q
q q
q q q q q qq
qq
Sample Quantiles
q q qq
q q q qq
q qq
q qq
qq
q q
q q q q q qq
qq
qq
q q q q q q q qqq qqq
qqq
qqq
q q
q q q q q
q q q q q qqq
qqq
qqq
q q q q q qq
qq
q
qqq
qq
0
q q qq
0
q q q q
qq q
q q q
q q qq
qqq
q
q q q q q q q q q qqq
qqq
qq
q q q q q q q q qqqqq
qqq
q q q
qq qq
qq
q
q q qq
q q qq
q q
q
−2
q
−2
q q
q q
q q q qq qqq
q q
q q
−4
−4
q q
q
−2 −1 0 1 2
Variable exogène (X) Theoretical Quantiles
46

47. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Analyse graphique des r´sidus, suite
e
Graphique des r´sidus εi = Yi − X i β versus Xi
e
Distribution asym´trique des r´sidus, pr´sence d’h´t´rog´n´it´ (e.g.
e e e ee e e e
hommes/femmes)
q
q
3
4
q
qq
q q
q
q qq
q
q q
q qq
q
qq
2
q
q q q qq
qq
q q q q
q qq
qq
qq
2
q q q q q
q q q q q qqq q
qq
q
q
Sample Quantiles
q q q
q q qq q q q
q
q
q
qq q q qq qq
qq
1
0
0
qq q q q q
q qq
q q q q q qq q q q q
q q q qq q q q q
q q q q q q q q q
q q q q
q
−2
qq q q q
−1
q q
q q qq
qq
qq
q
q q q qq
qqq
qq
q q q
qqq
q q q qq
qq
qq
qqqq
qqq
qqq
qqq
qqq
q
qqqq
qqq
−2
qq
−4
qq
q
qq qq
q q q
−3
−2 −1 0 1 2
Variable exogène (X) Theoretical Quantiles
47

48. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Analyse graphique des r´sidus, suite
e
Graphique des r´sidus εi = Yi − X i β versus Xi
e
Pr´sence d’une tendance, i.e. relation nonlin´aire pour X OOO OOO OOO OOO
e e
q
q
q q
4
qq
q
q q qq
q
q q qq
qq
2
qq q
q q q
q q q
q
q q q q qq
qq
2
q q qq
qq
qq
q
q q qq
q
Sample Quantiles
q q q q
q q qq q qq
q q q qq
qq qq
q qq
qqq
q q q q qq
q
q q q q q
qq
q q q
0
q q q q
q q qq
qq
q
0
q q qq
q
q q
q qq q q q qq
qq
qq
q q q q qq
qq
q q q q qq
q q
q q q q
q
q q q
q
qq q q
q qq
q
qqq
qq
q q q
q q q q q q qq
qq
−2
q
qqq
q qq
−2
q q
q q q
q q
q q
q qqq
qq
q q
−4
q
−4
q
−2 −1 0 1 2
Variable exogène (X) Theoretical Quantiles
48

49. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Analyse graphique des r´sidus, suite
e
Graphique des r´sidus εi = Yi − X i β versus Xi
e
Rupture de la s´rie, i.e. pr´sence d’un seuil (relation non-lin´aire en X, distinguer
e e e
Xi < u et Xi > u
q
q q
qq
q
4
qq
2
qq
q
q q
qq
q q q
q
q q
q q qq
qqq
q
q q
2
q q
1
q q
qq
q q
q qq
qq
q q
Sample Quantiles
q q q
q q q
q qq q q
q
q
q
q q q q q q q q q
q
q
qq q qq q q
qq
q q q qq
q
q q q qq
0
q q q q q q
0
q q q
q qqq q q q q
qqq q q q qq
qq
q q q q q q qq
qq
qq
q
q q qq
qq
qq
q q q
q
q q q q q q
q q q q qq q
q q q
q
−1
q q q
q q qq
q qq
q
−2
q q q q qq
q
qqq
qq
qq
q qq
q q
q q
−2
qqqq
−4
q
q q
−3
q
−2 −1 0 1 2
Variable exogène (X) Theoretical Quantiles
49

50. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Analyse graphique des r´sidus, suite
e
Graphique des r´sidus εi = Yi − X i β versus Xi
e
r´sidus autosc´dastiques, la variance croˆ avec X, V ar(εi ) = σ 2 Xi ou
e e ıt
V ar(εi ) = σ 2 Xi , ...etc.
2
q q
q
4
q q q
q q
qq
2
q q
q
q q qq
qq
2
q qq
qq
qqq
qq
Sample Quantiles
q q q q qqq
qq
qq
q q q q q
q q q q q q q q q qq
qq
q
q q q qq
q
q q q q q qq
qq
q
qq
0
q q q q qq
qq
q q q qq
qq
qq
q qq
qq
0
q q qq q q q qq
q
q qq qq
q q q q qq
qq
qq
q q q
q q q q q qq
qq
q q q q q qq
qq
qq
q q qq q qq
q q q
q q q q q qq
qq
q q
q q qq
q q qq
−2
q q
qq
−2
q
q
q qq q
q q q q
q
q
q q qq
q
q
−4
q
−4
q
−2 −1 0 1 2
Variable exogène (X) Theoretical Quantiles
50

51. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Analyse graphique des r´sidus, suite
e
Graphique des r´sidus εi = Yi − X i β versus Xi
e
r´sidus autocorr´l´s, ce qui arrive souvent avec des s´ries temporelles OOO OOO
e ee e
OOO OOO OOO
q
q
3
4
q
qq
q q
q
q qq
q
q q
q qq
q
qq
2
q
q q q qq
qq
q q q q
q qq
qq
qq
2
q q q q q
q q q q q qqq q
qq
q
q
Sample Quantiles
q q q
q q qq q q q
q
q
q
qq q q qq qq
qq
1
0
0
q q
q q q q q q q
q qq q q q
q
q qq q q
q q q q qq q q q q q q q
q q q q q q q q
q
−2
qq q q q
−1
q q
q q qq
qq
qq
q
q q q
qqqq
qqq
q q qq
q q q qq
qq
qq
q qqqq
qqqq
qqq
qqq
qqq
q
qqqq
qqq
−2
qq
−4
qq
q
q
q qq
q q q
−3
−2 −1 0 1 2
Variable exogène (X) Theoretical Quantiles
51

52. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Exemple : tester l’hypoth`se d’homosc´dasticit´
e e e
Tester l’hypoth`se d’homosc´dasticit´ est d´licat : il faut sp´cifier une alternative.
e e e e e
Par exemple, au lieu d’avoir Var(ε|X) = σ 2 on pourrait avoir
Var(ε|X) = σ 2 h(α0 + α1 X 2 ) Le test de Breusch-Pagan revient ` tester
a
H0 : α1 = 0 (homosc´dasticit´) contre H0 : α1 = 0 (h´t´rosc´dasticit´).
e e ee e e
L’id´e est d’utiliser un test du score (appel´ aussi test du multiplicateur de
e e
Lagrange), dans un mod`le e
Y = β0 + β1 X + ε o` ε2 = γ0 + γ1 X + η.
u
La proc´dure g´n´rale est simple,
e e e
• faire la r´gression Y = β0 + β1 X1 + · · · + βk Xk + ε
e
• sur ε, faire la r´gression ε2 = γ0 + γ1 X1 + · · · + γk Xk + η
e
• tester si γ1 = · · · = γk = 0, i.e. test de significativit´ globale de Fisher,
e
i.e. T = nR2 qui suit (sous H0 ) une loi χ2 (k)
> library(lmtest)
> bptest(REG)
52

53. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
studentized Breusch-Pagan test
data: model1
BP = 10.2903, df = 8, p-value = 0.2452
On peut le faire ` la main pour v´rifier
a e
> E=residuals(REG)
> REG2=lm(E^2~cars$speed)
> summary(REG2)$r.squared*50
[1] 3.21488
> 1-pchisq(summary(REG2)$r.squared*50,1)
[1] 0.07297155
> summary(REG2)
Call:
lm(formula = E^2 ~ cars$speed)
Residuals:
Min 1Q Median 3Q Max
-388.45 -175.07 -96.03 22.56 1607.53
53

54. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -61.05 167.56 -0.364 0.7172
cars$speed 18.71 10.30 1.816 0.0756 .
---
Signif. codes: 0 *** 0.001 ** 0.01 * 0.05 . 0.1 1
Residual standard error: 381.3 on 48 degrees of freedom
Multiple R-squared: 0.0643, Adjusted R-squared: 0.0448
F-statistic: 3.298 on 1 and 48 DF, p-value: 0.0756
Remarque On reviendra par la suite sur les mod`le permettant de prendre en
e
compte de l’h´t´rosc´dasticit´.
ee e e
54

55. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Tester l’ind´pendance des r´sidus
e e
Tester l’ind´pendance des r´sidus n´cessite d’expliciter la forme de l’alternative.
e e e
Par exemple, au lieu d’avoir cor(εi , εi+1 ) = 0 on pourrait avoir cor(εi , εi+1 ) = r
(= 0).
La statistique de Durbin-Watson est bas´e sur
e
(εi − εi−1 )2
DW =
(εi )2
qui est dans le package lmtest, via la fonction dwtest.
> library(lmtest)
> REG=lm(dist~speed,data=cars)
> dwtest(REG)
Durbin-Watson test
data: reg
DW = 1.6762, p-value = 0.09522
alternative hypothesis: true autocorrelation is greater than 0
55

56. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Les r´sidus sont ici ordonn´s comme dans la base. On pourrait suspecter un lien
e e
avec les X. Dans ce cas, on peut faire une r´gression sur la base r´ordonn´e.
e e e
> indice=rank(cars$speed,ties.method="random")
> reg=lm(dist~speed,data=cars[indice,])
> dwtest(reg)
Durbin-Watson test
data: reg
DW = 1.7993, p-value = 0.1935
alternative hypothesis: true autocorrelation is greater than 0
On va accepter ici l’hypoth`se d’absence d’autocorr´lation des r´sidus.
e e e
56

57. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Tester l’ind´pendance spatiale des r´sidus
e e
Pour des donn´es spatiales, on devra se contenter de regarder si, visuellement,
e
l’ind´pendance spatiale est une hypoth`se qui semble valide,
e e
> US=read.table("http://freakonometrics.free.fr/US.txt",
+ header=TRUE,sep=";")
> abreviation=read.table(
+ "http://freakonometrics.blog.free.fr/public/data/etatus.csv",
> header=TRUE,sep=",")
> US$USPS=rownames(US)
> US=merge(US,abreviation)
> US$nom=tolower(US$NOM)
> library(maps)
> VL0=strsplit(map("state")$names,":")
> VL=VL0[[1]]
> for(i in 2:length(VL0)){VL=c(VL,VL0[[i]][1])}
> ETAT=match(VL,US$nom)
57

58. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
On peut faire une fonction mettant de la couleur appropri´e dans chacune des
e
´tats,
e
> library(RColorBrewer)
> carte=function(V=US$Murder,titre=
+ "Taux d’homicides aux Etats-Unis"){
+ variable=as.numeric(as.character(cut(V,
+ quantile(V,seq(0,1,by=1/6)),labels=1:6)))
+ niveau=variable[ETAT]
+ couleur=rev(brewer.pal(6, "RdBu"))
+ noml=levels(cut(V,quantile(V,seq(0,1,by=1/6))))
+ map("state", fill = TRUE, col=couleur[niveau]);
+ legend(-78,34,legend=noml,fill=couleur,
+ cex=1,bty="n");
+ title(titre)}
58

59. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
>
>
> carte(US$Frost, titre="Nombre de jours de gel par an")
Nombre de jours de gel par an
(0,45]
(45,83]
(83,114]
(114,127]
(127,159]
(159,188]
59

60. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
> reg=lm(Murder~.-NOM-USPS-nom,data=US)
> regs=step(reg)
> carte(residuals(regs), titre="Rsidus de la rgression")
Résidus de la régression
(−3.3,−1.75]
(−1.75,−0.741]
(−0.741,−0.112]
(−0.112,0.744]
(0.744,1.67]
(1.67,3.47]
60

61. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Choix de mod`le, AIC et SIC/BIC
e
Le crit`re d’Akaike, not´ souvent AIC
e e
n
1
AIC = 2k − 2 log(L) = 2k + n log 2π ε2
i +1
n i=1
dans le cas Gaussien.
Le crit`re de Schwarz, not´ SIC (Schwarz Information Criterion), ou crit`re
e e e
Bay´sien, not´ BIC
e e
n
BIC = −2 log(L) + k ln(n) = n ln ε2
i + k ln(n).
i=1
> AIC(reg)
[1] 419.1569
> logLik(reg)
’log Lik.’ -206.5784 (df=3)
61

62. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Choix de mod`le : s´lection des variables
e e
Parfois on dispose de beaucoup de variables explicatives, et on ne sait quel
mod`le choisir.
e
dodge=read.table("http://perso.univ-rennes1.fr/arthur.charpentier/dodge.csv",
header=TRUE,sep=",")
La variable FIRE correspond au nombre d’incendies (/1000 m´nages) dans le
e
quartier i = 1, · · · , 47 de Chicago, en 1975. X1 est la proportion d’habitations
construites avant 1940, X2 le nombre de vols commis, et X3 le revenu m´dian du
e
quartier.
62

63. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Choix de mod`le : s´lection des variables
e e
Les 8 mod`les possibles sont les suivants
e
(0) Y = β0 + ε
(1) Y = β0 + β1 X1 ε
(2) Y = β0 + β2 X2 ε
(3) Y = β0 + β3 X3 ε
(12) Y = β0 + β1 X1 + β2 X2 ε
(13) Y = β0 + β1 X1 + β3 X3 ε
(23) Y = β0 + β2 X2 + β3 X3 ε
(123) Y = β0 + β1 X1 + β2 X2 + β3 X3 ε
63

64. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Choix de mod`le : s´lection des variables
e e
2
mod`le
e R2 R log L AIC degr´s libert´
e e
(0) 0.0000 0.0000 -166.4638 336.9277 1
(1) 0.1423920 0.1233340 -162.8540537 331.7081074 2
(2) 0.1355551 0.1163452 -163.0406536 332.0813071 2
(3) 0.2522118 0.2355942 -159.6339128 325.2678255 2
(12) 0.2276727 0.1925669 -160.3926938 328.7853875 3
(13) 0.2703887 0.2372245 -159.0556280 326.1112560 3
(23) 0.4414889 0.4161020 -152.7755479 313.5510959 3
(123) 0.4416723 0.4027192 -152.7678305 315.5356609 4
Dans ce cas, le meilleur mod`le est le mod`le Y = β0 + β2 X2 + β3 X3 + ε, quel
e e
que soit le crit`re de choix.
e
64

65. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Choix de mod`le : s´lection des variables
e e
(23) (123) (0)
335
(23)
0.4
(123)
(2)
(1)
330
0.3
(12)
(13)
(3)
(3) (13) (13)
325
(12) (3)
0.2
(12)
(1)
(2)
320
(1)
(2)
0.1
(123)
315
0.0
(0) (0) (23)
1.0 1.5 2.0 2.5 3.0 3.5 4.0 1.0 1.5 2.0 2.5 3.0 3.5 4.0
degrés de liberté degrés de liberté
Une s´lection automatique bas´e sur un minimisation du AIC peut ˆtre faite, soit
e e e
backward ` partir du mod`le complet, soit forward ` partir du mod`le le plus
a e a e
simple.
65

66. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Choix de mod`le : s´lection des variables
e e
> step(lm(Fire~.,data=D),direction = "backward")
Start: AIC=180.16
Fire ~ X_1 + X_2 + X_3
Df Sum of Sq RSS AIC
- X_1 1 0.60 1832.36 178.17
<none> 1831.75 180.16
- X_2 1 561.94 2393.70 190.73
- X_3 1 702.09 2533.84 193.41
Step: AIC=178.17
Fire ~ X_2 + X_3
Df Sum of Sq RSS AIC
<none> 1832.36 178.17
- X_2 1 620.98 2453.33 189.89
- X_3 1 1003.70 2836.06 196.70
Call:
66

67. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
lm(formula = Fire ~ X_2 + X_3, data = D)
Coefficients:
(Intercept) X_2 X_3
21.4965 0.2213 -1.5248
67

68. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Exemple d’application : cigarettes et esp´rance de vie
e
´
Etudions ici le lien entre l’esp´rance de vie et la consommation de cigarette (par
e
tˆte)
e
q
q q
q
q q q q q
q q q q
q q q q
70
q q q
q
q
q q
q q q q
q
Espérance de vie à la naissance
q qq q
q q q
q q
q q q
q q q q q q
q q
q qq q q
60
q q q
q q q q q q q
q q q
q q
q q
q
qq q
q q
q q
50
q
q q
q qq
q q
q
q
q q
q q
40
q q
qq
q
qq q
q
30
0 1000 2000 3000 4000
Consommation de cigarettes
68

69. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Exemple d’application : cigarettes et esp´rance de vie
e
> summary(lm(Y~X))
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4.799e+01 1.371e+00 34.995 < 2e-16 ***
X 8.528e-03 9.007e-04 9.468 1.33e-15 ***
---
Signif. codes: 0 ’***’ 0.001 ’**’ 0.01 ’*’ 0.05 ’.’ 0.1 ’ ’ 1
Residual standard error: 8.158 on 101 degrees of freedom
(86 observations deleted due to missingness)
Multiple R-Squared: 0.4702, Adjusted R-squared: 0.465
F-statistic: 89.64 on 1 and 101 DF, p-value: 1.333e-15
Interpr´tation (rapide et sans doute falacieuse) : β1 ∼ 0.00852, i.e. en fumant une
e
cigarette de plus par an, on augmente l’esp´rance de vie de 0.00852 ann´es.
e e
Aussi, fumer 1 cigarette de plus (ou de moins) par jour augmente (ou diminue)
l’esp´rance de vie de 3.11 ann´es.
e e
69

70. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Exemple d’application : cigarettes et esp´rance de vie
e
´
Etudions ici le lien entre l’esp´rance de vie et la consommation de cigarette (par
e
tˆte)
e
q
q q
q
q q q q q
q q q q
q q q q
70
q q q
q
q
q q
q q q q
q
Espérance de vie à la naissance
q qq q
q q q
q q
q q q
q q q q q q
q q
q qq q q
60
q q q
q q q q q q q
q q q
q q
q q
q
qq q
q q
q q
50
q
q q
q qq
q q
q
q
q q
q q
40
q q
qq
q
qq q
q
30
0 1000 2000 3000 4000
Consommation de cigarettes
70

71. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Exemple d’application : cigarettes et esp´rance de vie
e
L’interpr´tation est bien entendu fausse et vient du type de donn´es utilis´´es
e e ee
> head(dl,10)
X Country Continent LE CigCon
1 1 Afghanistan Asia 35.5 98
2 2 Albania Europe 61.4 NA
3 3 Algeria Africa 60.6 1021
4 4 Andorra Europe 72.2 NA
5 5 Angola Africa 33.4 571
6 6 Antigua and Barbuda South America 61.9 NA
7 7 Argentina South America 65.3 1495
8 8 Armenia Europe 61.0 1095
9 9 Australia Australia 72.6 1907
10 10 Austria Europe 71.4 2073
Les consommations les plus ´lev´es de cigarettes sont observ´es dans les pays les
e e e
plus riches, o` l’esp´rance de vie est la plus grande.
u e
Remarque Une r´gression lin´aire est l’ananlyse d’une corr´lation et pas d’une
e e e
relation de causalit´.
e
71

72. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Tester la normalit´
e
Tous les r´sultats ont ´t´s obtenus sous l’hypoth`se de normalit´ des r´sidus.
e ee e e e
Regression residuals Regression residuals
0.030
1.0
q
q
q
q
q
q
q
0.025
q
q
q
0.8
q
q
q
q
q
0.020
q
q
q
q
q
0.6
q
q
0.015
q
q
q
q
q
q
q
0.4
q
q
0.010
q
q
q
q
q
q
q
q
0.2
0.005
q
q
q
q
q
q
q
q
0.000
q
q
0.0
−20 0 20 40 −20 0 20 40
72

73. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Tester la normalit´
e
Le test de Kolmogorov Smirnov permet de tester l’ajustement d’un loi normale
N (0, 152 ) pour les r´sidus,
e
> ks.test(reg$residuals, "pnorm", 0,15)
One-sample Kolmogorov-Smirnov test
data: E
D = 0.128, p-value = 0.3859
alternative hypothesis: two-sided
Warning message:
In ks.test(E, "pnorm", 0, 15) : cannot compute correct p-values with ties
73

74. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Rappelons que le test de Kolmogorov Smirnov, de l’hypoth`se H0 : F = F
e
(contre l’hypoth`se alternative H0 : F = F ) est bas´ sur la statistique
e e
D = sup F (x) − Fn (x) ,
x∈R
Le th´or`me de Glivenko-Cantelli garantissant que
e e
p.s.
sup F (x) − Fn (x) −→ 0
x∈R
lorsque n → ∞, sous H0 , i.e. si F est effectivement la vraie loie.
Mais formellement ce n’est pas un test de normalit´ : on teste ici
e
H0 : F = N (µ , σ 2 ) et non pas H0 : F = N ( , ).
74

75. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Tester la normalit´
e
> shapiro.test(reg$residuals)
Shapiro-Wilk normality test
W = 0.9451, p-value = 0.02153
> ad.test(reg$residuals)
Anderson-Darling normality test
A = 0.7941, p-value = 0.0369
Ces tests sont techniques, et sont d´taill´s dans les livres des statistiques (cf blog).
e e
Le test de Cram´r-von-Mises repose sur
e
∞
nW 2 = n [F (x) − F (x)]2 dF (x)
−∞
75

76. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
soit, en pratique
n 2
2 1 2i − 1
T = nW = + − F (xi:n ) ,
12n i=1 2n
o` F est la loi th´orique que l’on cherche ` tester, i.e. Φ.
u e a
> cvm.test(reg$residuals)
Cramer-von Mises normality test
W = 0.1257, p-value = 0.0483
> pearson.test(reg$residuals)
Pearson chi-square normality test
P = 8.4, p-value = 0.2986
Le test de Jarque-Bera repose sur
n 2 (K − 3)2
JB = S + ,
6 4
76

77. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
o` n est le nombre de degr´s de libert´s, S est la skewness empirique, et K la
u e e
kurtosis empirique,
1 n 3
µ3 µ3 n i=1 (xi − x)
¯
S= 3 = =
σ (σ 2 )3/2 1 n 2
3/2
n i=1 (xi − x)
¯
1 n 4
µ4 µ4 n i=1 (xi − x)
¯
K= 4 = =
σ (σ 2 )2 1 n 2
2
n i=1 (xi − x)
¯
Sous H0 (normalit´), JB ∼ χ2 (2).
e
> jarque.bera.test(reg$residuals)
Jarque Bera Test
X-squared = 8.1888, df = 2, p-value = 0.01667
77

78. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Tester la pr´sence d’une rupture, le test de Chow
e
Le test de Chow permet de tester une rupture en sp´cifiant explicitement la
e
rupture. Le test de Chow est simplement un test de Ficher, o` on compare des
u
sous-mod`les ` un mod`le global. On suppose ici
e a e
 
 β pour i = 1, · · · , i  H :β =β
1 0 0 1 2
β= et on teste
 β pour i = i0 + 1, · · · , n  H1 : β = β
2 1 2
i0 est ici un point entre k et n − k (il faut garder suffisement d’observations pour
mener le test). Chow (1960) sugg`re un test de la forme
e
η η−εε
Fi0 =
ε ε/(n − 2k)
o`
u
εi = Yi − X i β pour i = k, · · · , n − k

 Y − X β pour i = k, · · · , i
i i 1 0
ηi =
 Yi − X β pour i = i0 + 1, · · · , n − k
i 2
78

79. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
La fonction Fstats repr´sente ainsi Fi0 pour toutes les valeurs entre k et n − k
e
(par d´faut, 30% des observations sont retir´es, 15% ` gauche 15% ` droite).
e e a a
> reg1=lm(formula = dist ~ speed, data = cars[1:26,])
> S1=sum(reg1$residuals^2); DL1=reg1$df.residual
> reg2=lm(formula = dist ~ speed, data = cars[27:50,])
> S2=sum(reg2$residuals^2); DL2=reg2$df.residual
> reg0=lm(formula = dist ~ speed, data = cars[1:50,])
> S0=sum(reg0$residuals^2); DL0=reg0$df.residual
> ((S0-(S1+S2))/(DL0-(DL1+DL2)-1))/(S0/(DL0-1))
[1] 2.601249
79

80. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Tester la pr´sence d’une rupture, le test de Chow
e
Fstats(dist ~ speed,data=cars,from=7/50)
12
120
q
10
100
q
q
q q
8
Distance de feinage
80
q
q
F statistics
q
q
q
q
6
60
q
q q
q q
q
q
q
q q
4
q
40
q q
q q
q q
q q q
q
q q
q q q
q
q
2
q
20
q q
q q
q
q
q q
q
q
0
0
5 10 15 20 25 0 10 20 30 40 50
Vitesse du véhicule Indice
80

81. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Tester la pr´sence d’une rupture, le test de Chow
e
Fstats(dist ~ speed,data=cars,from=2/50)
120
q
12
100
q
10
q
q q
Distance de feinage
80
q
q
8
F statistics
q
q
q
q
60
q
q q
6
q q
q
q
q
q q
q
40
q q
4
q q
q q
q q q
q q
q q q q
q
q q
20
q q
2
q q
q
q
q q
q
q
0
0
5 10 15 20 25 0 10 20 30 40 50
Vitesse du véhicule Indice
81

82. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Tester la pr´sence d’une rupture, le test de Chow
e
Si l’on ne sait pas ` quelle date la rupture a eu lieu, des outils de type CUSUM
a
peuvent ˆtre utilis´s (cf Ploberger & Kr¨mer (1992)). Pour t ∈ [0, 1], on pose
e e a
nt
1
Wt = √ εi .
σ n i=1
Dans ce test, si α est le niveau de confiance, les bornes g´n´ralement consid´r´es
e e ee
sont ±α. En fait, les bornes th´oriques sont plutˆt de la forme ±α t(1 − t).
e o
Sous R, il suffit de sp´cifier type=’’OLS-CUSUM’’ dans la fonction efp.
e
cusum <- efp(dist ~ speed, type = "OLS-CUSUM",data=cars)
plot(cusum,ylim=c(-2,2))
plot(cusum, alpha = 0.05, alt.boundary = TRUE,ylim=c(-2,2))
82

83. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
2 OLS−based CUSUM test OLS−based CUSUM test with alternative boundaries
2
Empirical fluctuation process
Empirical fluctuation process
1
1
0
0
−1
−1
−2
−2
0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0
Time Time
Les points sont ici tri´s par vitesse. Aussi, une rupture d´tect´e en t = 92%
e e e
signifie qu’il y a une rupture dans la mod´lation lin´ire de Y par X ` partir de la
e a a
tn = 46`me observation.
e
83

84. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Intervalles de confiance pour Y et Y
Supposons que l’on dispose d’une nouvelle observation X 0 et que l’on souhaite
pr´dire la valeur Y0 assoic´e.
e e
L’incertitude sur la pr´diction Y0 vient de l’erreur d’estimation sur les param`tres
e e
β.
L’incertitude sur la r´alisation Y0 vient de l’erreur d’estimation sur les
e
param`tres β et de l’erreur associ´e au mod`le lin´aire, i.e. ε0 .
e e e e
Dans le cas de la r´gression simple, Y0 = Y0 + ε0 = β0 + β1 X0 + ε0 . Aussi,
e
2
• Var(Y0 ) = Var(β0 ) + 2X0 cov(β0 , β1 ) + X0 Var(β1 )
• Var(Y0 ) = V ar(Y0 ) + Var(ε0 ), si l’on suppose que le bruit est la partie non
expliqu´e. Aussi Var(Y0 ) = Var(β0 ) + 2X0 cov(β0 , β1 ) + X0 Var(β1 ) + σ 2
e 2
84

85. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Intervalle de confiance pour Y
L’incertitude sur la pr´diction Yj vient de l’erreur d’estimation sur les param`tres
e e
β.
Dans ce cas, si l’on dispose d’une nouvelle observation X 0 , l’intervalle de
confiance pour Y0 = (X X)−1 X Y0 est
Y0 ± tn−k (1 − α/2)σ x0 (X X)−1 X 0
o` tn−k (1 − α/2) est le quantile d’ordre (1 − α/2) de la loi de Student ` n − k
u a
degr´s de libert´.
e e
85

86. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Intervalle de confiance pour Y
L’incertitude sur la r´alisation Yj vient de l’erreur d’estimation sur les
e
param`tres β et de l’erreur associ´e au mod`le lin´aire, i.e. εi .
e e e e
Dans ce cas, si l’on dispose d’une nouvelle observation X 0 , l’intervalle de
confiance pour Y0 = Y0 + ε0 est
Y0 ± tn−k (1 − α/2)σ 1+x0 (X X)−1 X 0
En fait, sous R, l’intervalle de confiance pour Y n’inclue pas l’erreur associ´e `
e a
l’erreur d’estimation, aussi, dans ce cas, si l’on dispose d’une nouvelle observation
X 0 , l’intervalle de confiance pour Y0 = Y0 + ε0 est
Y0 ± tn−k (1 − α/2)σ .
86

87. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Intervalles de confiance pour Y et Y
pp <- predict(lm(y~x,data=D), new=data.frame(x=seq(0,30)), interval=’prediction’)
pc <- predict(lm(y~x,data=D), new=data.frame(x=seq(0,30)), interval=’confidence’)
Confidence and prediction bands Confidence and prediction bands
120
120
q q
100
100
q
q q
q
q q q q
80
80
q q
q q
distance
distance
q q q q
q q q q
60
60
q q
q q q q q q q q
q q q q
q q q q q q
q q q q q q
40
40
q q q q q
q
q q q q q q
q
q
q q q q q q
q q q q q q q
q
q q
20
20
q q q q q
q q q q q
q q
q q q q
q q q q
0
0
5 10 15 20 25 5 10 15 20 25
car speed car speed
87

88. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
250
200
150
Intervalles de confiance pour Y et Y
q
100
q
q q
q
q
q q
q q
q
q q q q
50
q q
q qq
qq q
q qq qq
q
q
qqqqqq
q
q
q qqq q
q
q q
q q
0
0 20 40 60 80
88

89. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Mod`le lin´aire, ou multiplicatif ?
e e
Consid´rons le taux de mortalit´ infantile comme une fonction du PIB par tˆte.
e e e
Sierra.Leone
Afghanistan
q
q
150
Angola
q q
q
Chad
Côte.dIvoire
Somalia
Democratic.Republic.of.the.Congo
q
Taux de mortalité infantile
Guinea−Bissau
qq
Nigeria
q
q
q
qq
Burkina.Faso
Guinea
q
100
q
Benin
Central.African.Republic
Mozambique
q
q
q Equatorial.Guinea
q
Togo
Malawi
q q
Djibouti
q
qqqq
q
Turkmenistan
Gambia
Azerbaijan
q United.Republic.of.Tanzania
Congo
qq
q qq
Timor−Leste
Pakistan
Madagascar
Myanmar q
Lesotho
Sudan
Kenya q
Cambodia
qq
Papua.New.Guinea
qq
Tajikistan
q
q
Yemen
qq
Zimbabwe
Ghanaq
q
India
Solomon.Islands Gabon
q
Kyrgyzstan
q
Bangladesh
q
Laos
q
qq
q
Haiti
q
Korea q
Comoros
q
50
q
Bolivia
Bhutan
q Namibia
Guyana
q
Mongolia q
qqq q
q q
q
Marshall.Islands
qqGrenada
Micronesia.(Federated.States.of)
Tuvalu
Paraguayq
Algeria
Morocco
Iran
Guatemala
Egypt q
Niueq Turkey
qqq
Armenia
Honduras q
Suriname
Indonesia
qq qq
q q
Cape.Verde
qqq
q
Kazakhstan
China q
Saint.Vincent.and.the.Grenadines
Montenegro
qq Fiji
El.Salvador
Samoa
NicaraguaPeru
Tunisia
Viet.Nam
Jordanq q
Albaniaq
Occupied.Palestinian.Territory Saudi.Arabia
Libyan.Arab.Jamahiriya
q qqVenezuela
q qqq q
Russian.Federation
Republic.of.Moldova
Syrian.Arab.Republic
qqq q
qBelize
qq
Macedonia
Romania
Jamaica Netherlands.Antilles
q
RéunionMauritius
Argentina
Uruguay
Ukraineqq qq
qBulgaria
Bosnia.and.Herzegovina Cook.Islands
Serbiaq
American.Samoa
Sri.Lanka q Lithuania Oman
qq qq qLatvia
Thailand
Bahamas q French.Guiana
Malaysia
Belarus q Chile
Guam Poland q q qq
French.Polynesia q United.States.Virgin.Islands
Martiniqueq Slovakia Malta New.CaledoniaGreeceUnited.Arab.Emirates
q qqq q
q qq q q Czech.Republic
q Estonia q Slovenia Cyprus
q Puerto.Rico
Brunei.Darussalam United.States.of.America
United.Kingdomq
Italy FranceFinland
Qatar
Luxembourg Liechtenstein
Channel.Islands q q
Cuba q
qq q Republic.of.Korea
Israelq Singaporeqq Netherlands
q Canada Sweden San.Marino
Belgium
Austria
Japan Ireland
Denmark q Norway
Gibraltar q
q qq q qq
q q q q q q
q q
qq q
q q q q q
q q qq q q q qq q q q
q qq
q q q q
q q
q q q q q
0
0e+00 2e+04 4e+04 6e+04 8e+04 1e+05
PIB par tête
Visiblement le mod`le lin´aire ne convient pas.
e e
89

90. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Mod`le lin´aire, ou multiplicatif ?
e e
Transformation a priori : transformation logarithmique,
Sierra.Leone
Afghanistan
Liberia q Angola
Mali
q
Guinea−Bissau Somalia
Democratic.Republic.of.the.Congo Niger
Rwanda q Chad Côte.dIvoire
Nigeria q
Burkina.Faso q
Burundi q qGuinea
q Central.African.Republic
q q Mozambique BeninZambia q q
100
Malawi
Ethiopia Togo q
q CameroonIraq Equatorial.Guinea
q q
q q Djibouti
q q
q q Gambia q
Uganda qq Turkmenistan United.Republic.of.Tanzania
Sao.Tome.and.Principe q Azerbaijan Swaziland
Congo
Myanmar q
Timor−Leste qKenya Sudan
Madagascar CambodiaMauritania
q Pakistan
Senegal
Lesotho q q q
Tajikistan Papua.New.Guinea q q
Zimbabwe q q q qq q
Yemen
q
Ghana Solomon.Islands
q
q
Eritrea Nepal q Kyrgyzstan q India
q
Uzbekistan
BangladeshLaos
q q q Gabon
q q Haitiq q
Korea
Comoros q q
South.Africa q
50
q Western.Sahara Bolivia Bhutan Botswana
q qq q Kiribati Guyana Namibia
q Mongolia q q GeorgiaMarshall.Islands q
q qq
Taux de mortalité (log)
q
q q
Micronesia.(Federated.States.of)
Paraguay MoroccoMaldives Grenada
Tuvalu
q
Niue Egypt
Armenia q q q Algeria q
GuatemalaIran
Dominican.Republic
q Vanuatu
Honduras
Indonesia q q q q Suriname Turkey
q
q
q q q Cape.Verde
Philippines q
q Kazakhstan q
q Brazil
China Samoa Montenegro Lebanon
q Saint.Vincent.and.the.Grenadines
El.Salvador
Nicaragua q q TongaEcuador qq q Viet.Nam
Peru Fiji
Tunisia q
qColombia
q q
Jordan q
Albania q
Libyan.Arab.Jamahiriya Saudi.Arabia
20
q
Occupied.Palestinian.Territory q Panama
q Russian.Federation
q
Republic.of.MoldovaSyrian.Arab.Republicq q q
q q Belize Venezuela Mexico
q q q q q Aruba
Macedonia Romania q q
Netherlands.Antilles
q q q Mauritius
Réunion Ukraine q Jamaica Uruguay
q
Argentina
Saint.Lucia
Bahamas
q French.Guiana
Bosnia.and.Herzegovina q
Bulgaria
American.Samoa qq q
Serbia q Trinidad.and.Tobago q
Oman
q Sri.Lanka q Thailand q Cook.IslandsBahrain q
q q q Costa.Rica Latvia qq
Barbados q
q q q
10
BelarusGuam Malaysia Lithuania
q q q United.States.Virgin.Islands
Greenland
q q q Palau
q French.Polynesia q
United.Arab.Emirates Qatar
Kuwait q
Martinique Guadeloupe q SlovakiaHungary
Poland Estonia
Chile Puerto.Rico q q
q Greece q
q q qCroatia q q
q q q q
Cyprus
MaltaNew.Caledonia United.States.of.America
Brunei.Darussalam Liechtenstein
Channel.Islands Cuba q q Slovenia New.Zealand
Portugal q q Italy
q
Israel Canadaq Ireland
United.Kingdom
Netherlands Luxembourgq
q q q q
q q q qqq q q
5
Hong.Kong Belgium
Republic.of.Korea Spain Germany Switzerland
Czech.Republic France Denmark
Australia
Austria
Finland
q q q q qqq
qq qq
Turks.and.Caicos.Islands San.Marino Norway
SingaporeJapan
Sweden Iceland
q q q q q q q
Gibraltar Isle.of.Man
q q
2
1e+02 5e+02 1e+03 5e+03 1e+04 5e+04 1e+05
PIB par tête (log)
90

91. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Mod`le lin´aire, ou multiplicatif ?
e e
Transformation a priori : transformation logarithmique,
Sierra.Leone
Afghanistan
q
q
150
Liberia
Angola
Mali q
q
q
Chad
Côte.dIvoire
Somalia
Democratic.Republic.of.the.Congo
q
Guinea−Bissau
qq
Rwanda
Niger
Nigeria
q
q
q
qq
Burkina.Faso
Guinea
Taux de mortalité
q
100
Burundi
q
Benin
Central.African.Republic
Mozambique
qq
Zambia
q Equatorial.Guinea
q
Togo
Malawi
q
Cameroon
Ethiopia q
Djibouti
qq
qIraq
qq
Uganda q
Turkmenistan
Gambia United.Republic.of.Tanzania
Azerbaijan
Sao.Tome.and.Principe
q
Swaziland
Congo
qq
qq
Timor−Leste
Pakistan q
Madagascar
Myanmar
Senegal
Kenyaq
Lesotho
Sudan q
Mauritania
Cambodia
q
qq
Papua.New.Guinea
q
Tajikistan
q
q
Yemen
qq
Zimbabwe
Ghanaq
q
Uzbekistan
Eritrea
India
Solomon.Islands Gabon
Nepal
q
Kyrgyzstan
q
Bangladesh
q
Laos
q
qq
q
Haiti
q
Korea Botswana q
Comoros
q
50
q South.Africa
Bolivia
Bhutan
q Namibia
Western.Sahara
Guyana
q
Kiribati
Mongolia q
qq
Georgia
q q
q q
q
Marshall.Islands
qqGrenada
Micronesia.(Federated.States.of)
Maldives
Tuvalu
Paraguayq
Algeria
Morocco
Iran
Dominican.Republic
Guatemala
Egypt q
Niueq Turkey
qqq
Armenia
Honduras
Vanuatuq
Suriname
Indonesia
qq qq
q q
Cape.Verde
qq q
Kazakhstan
qq Brazil
Philippines q
q Peru
Saint.Vincent.and.the.Grenadines
ChinaLebanon
Montenegro
El.Salvador
Samoa
Nicaragua
Ecuador
Fiji
Tunisia
Viet.Nam
Tonga
Jordanqq
Albania
Occupied.Palestinian.Territory Saudi.Arabia
Colombiaq
Libyan.Arab.Jamahiriya
q qqVenezuela
q qqq Panama
q
MacedoniaMexico
Russian.Federation
Republic.of.Moldova
Syrian.Arab.Republic
qqq q
qBelize
q
Romania Aruba
Netherlands.Antilles
American.Samoa Barbadosq
q
Jamaica
Mauritius
Argentina
Uruguay
Ukraineqq qq
qBulgaria Trinidad.and.Tobago
RéunionSaint.Lucia Bahamas
Bosnia.and.Herzegovina Cook.Islands Bahrain q
Serbiaq
Sri.Lanka q Lithuania Oman
qqCosta.Rica
Thailand Latvia
qq qqPalau qq
French.Guiana
Malaysia Hungary
qBelarus Poland q qMalta French.Polynesia Greenland q United.States.Virgin.Islands
qqq q
Guam
Martiniqueq Chile
GuadeloupeSlovakia United.Arab.Emirates
Kuwait Qatar
q q q Estonia q
q Puerto.Rico
q qq
Hong.Kong Cuba q Czech.RepublicNew.CaledoniaGreece Italy Germany Sweden San.Marino
qq q q qq Slovenia Cyprus Singaporeq
Channel.Islands q Croatiaq Republic.of.Korea q
Portugal Brunei.Darussalam
Israelq New.Zealand
Spain q United.States.of.America
United.Kingdomq
Netherlands
q Canada
Belgium
FranceFinland
Australia
Austria
Japan Ireland
Denmark
Switzerland q Norway Luxembourg Liechtenstein
q q
Gibraltar q qqq q Turks.and.Caicos.Islands
q q
q q q q q
q q q q q q q Isle.of.Man Iceland
q q q
q q q q q qq q qq q
q qq q q q q
q q q
0
0e+00 2e+04 4e+04 6e+04 8e+04 1e+05
PIB par tête
91

92. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Mod`le sur Y ou log Y
e
La transformation param´trique la plus classique en ´conom´trie est la
e e e
transform´e de Box-Cox,
e
 −λ
 x − 1 pour λ = 0
f (x, λ) = λ
log(x) pour λ = 0

92

93. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Box−Cox transform
2
1
0
−1
−2
−3
−4
0 1 2 3 4
Cette transformation ne marche toutefois que pour les valeurs positives. Une
variante (propos´e dans le mˆme papier) est
e e
−λ
 [x + µ] − 1 pour λ = 0

f (x, λ, µ) = λ
log([x + µ]) pour λ = 0

93

94. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
En pratique, µ n’est pas consid´r´ comme un param`tre inconnu.
ee e
L’id´e est de transformer les donn´es de telle sorte que f (Y, λ ) soit
e e
approximativement normal pour un λ bien choisi.
Supposons que Y suive une loi exponentielle. La transformation de Box-Cox
donne alors une loi de Weibull...
94

95. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
L’objectif initial de l’analyse de Box-Cox ´tait d’estimer un coefficient λ optimal
e
• la premi`re id´e a ´t´ d’utiliser la m´thode du maximum de vraisemblance.
e e ee e
Grce aux propri´t´s asymptotiques, on peut ´galement obtenir un intervalle de
ee e
confiance approch´. e
• la seconde id´e (propos´e d`s 1964) a ´t´ d’utiliser la m´thode bay´sienne.
e e e ee e e
Dans l’approche par maximum de vraisemblance, on suppose que
Y λ = f (Y, λ) ∼ N (Xβ, σ 2 I).
La vraisemblance du mod`le s’´crit alors
e e
−(Y λ − Xβ) (Y λ − Xβ)
L(λ, β, σ 2 |Y, X) = (2πσ 2 )−n/2 exp J(λ, Y )
2σ 2
o` J(λ, Y ) d´signe le Jacobien de la transformationn Y → Y λ = f (Y, λ), i.e.
u e
n
J(λ, Y ) = Yiλ−1 .
i=1
95

96. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Notons que - conditionnellement ` λ on retrouve le mod`le lin´aire gaussien
a e e
classique, et donc les estimations du maximum de vraisemblance pour le couple
(β, σ 2 ) sont
˜
β λ = (X X)−1 X Y λ ,
˜ 1
σ 2 λ = Y λ [I − X(X X)−1 X ]Y λ ,
n
La fonction
˜ ˜2
V P : λ → L(λ, β λ , σλ |Y, X)
est appel´e vraisemblance profil´e (profile likelihood). Notons que
e e
n
n
σ2
log V P (λ) = constant − log(˜λ ) + [λ − 1] log(Yi ).
2 i=1
Comme nous avons pu ´crire la vraisemblance, notons qu’il est possible de faire
e
toute sorte de tests, en particulier des tests de rapport de vraisemblance,
96

97. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Pour test H : λ = λ0 , on utilise la statistique du rapport de vraisemblance
L
W = 2[log V P (λ) − log V P (λ0 )] → χ2 (1)
Remarque Au del` de la transform´e de Box-Cox, il existe aussi la transform´e
a e e
dite de Box-Tidwell, correpondant ` une fonction puissance.
a
97

98. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Faire une pr´diction avec un mod`le logarithmique
e e
Si on retient l’id´e d’un mod`le lin´aire sur log Y , cela ne donne pas (pour
e e e
l’instant) un mod`le pour Y . D’apr`s l’in´galit´ de Jensen, on va toujours sous
e e e e
estimer la valeur en prenant l’exponentielle de la valeur pr´dite par le mod`le
e e
logarithmique.
Si Y ∼ N (µ, σ 2 ) avec E(Y ) = µ
alors exp(Y ) ∼ LN (µ, σ 2 ) mais E(exp(Y )) = exp(µ) car
1
E(exp(Y )) = exp µ+ σ 2 .
2
> reg1=lm(dist~speed,data=cars)
> reg2=lm(log(dist)~speed,data=cars)
> newcars=data.frame(speed=seq(1,26,by=.1))
98

99. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
> p1=predict(reg1,newdata=newcars)
> p2=exp(predict(reg2,newdata=newcars))
>
120
120
q q
100
100
q
q q
q
q q q q
80
80
q q
q q
q q
q q
q q
q q
dist
dist
60
60
q q
q q q q
q q q q
q q
q q
q q
q q q q
q q
40
40
q q q q
q q q q
q q q q
q q q q q q
q q q q
q q q q q q q q
q q
q q
20
20
q q q q
q q q q
q q
q q
q q q q
q q
q q
0
0
5 10 15 20 25 5 10 15 20 25
speed speed
99

100. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
> p1=predict(reg1,newdata=newcars)
> p2b=exp(predict(reg2,newdata=newcars)
+ .5*summary(reg2)$sigma^2)
120
120
q q
100
100
q
q q
q
q q q q
80
80
q q
q q
q q
q q
q q
q q
dist
dist
60
60
q q
q q q q
q q q q
q q
q q
q q
q q q q
q q
40
40
q q q q
q q q q
q q q q
q q q q q q
q q q q
q q q q q q q q
q q
q q
20
20
q q q q
q q q q
q q
q q
q q q q
q q
q q
0
0
5 10 15 20 25 5 10 15 20 25
speed speed
100

101. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
La r´gression pond´r´e
e e e
L’id´e des moindres carr´s pond´r´s (weighted least squares) consiste ` chercher `
e e ee a a
minimiser
n
ωi [Yi − (β0 + β1 Xi,1 + · · · + βk Xi,k )]2
i=1
Notons Ω la matrice diagonale Ω = [Ωi,j ] avec Ωi,j = ωi δi=j . Dans ce cas, la
condition du premier ordre (´quations normales) s’´crit
e e
X ΩX β = X ΩY .
Si on pose W = Ω1/2 i.e. Ω = W W , alors
X W WX β = X W WY .
˜ ˜
i.e. si X = W X et Y = W Y
˜ ˜ ˜ ˜
X X β=X Y,
qui est la condition du premier ordre pour un mod`le lin´aire standard.
e e
101

102. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Application : prise en compte de l’h´t´rosc´dasticit´
e e e e
2
Si l’on suppose que V ar(εi ) = γXi,j o` γ > 0 pour un j = 1, · · · , k, alors on
u
cherche a minimiser
`
n
1
2 [Yi − (β0 + β1 Xi,1 + · · · + βk Xi,k )]2 .
i=1
Xi,j
La m´thode naturelle pour estimer les coefficients consiste ` consid´rer des
e a e
moindres carr´s ordinaires sur la r´gression
e e
Yi 1 Xi,1 Xi,k εi
= α0 + α1 + · · · + αk + .
Xi,j Xi,j Xi,j Xi,j Xi,j
Notons que pour j = i, 0, αj est un estimateur de βj , αj est un estimateur de β0 ,
et α0 est un estimateur de βj .
102

103. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Application : r´gression locale, et lissage
e
Rappelons qu’un esp´rance conditionnelle est l’esp´rance associ´e ` la loi
e e e a
conditionnelle, i.e.
fY,X (u, x) yfY,X (u, x)du
ϕ(x) = E(Y |X = x) = yfY |X=x (u|x)du = y du =
fX (x) fX (x)
Tukey (1961) a propos´ de transposer l’histogramme au ` l’approximation de
e a
l’esp´rance conditionelle.
e
Soit (Bj )j=1,·,m une partition du support de X,
n
Yi 1(Xi ∈ Bj )
i=1
ϕ(x) = n pour tout x ∈ Bj .
1(Xi ∈ Bj )
i=1
On parle de r´gressogramme, propos´ par Tukey (1961)
e e
103

104. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
120
120
q q
100
100
q
q q
q
q q q q
distance de freinage
distance de freinage
80
80
q q
q q
q q
q q
q q
q q
60
60
q q
q q q q
q q q q
q q
q q
q q
q q q q
q q
40
40
q q q q
q q q q
q q q q
q q q q q q
q q q q
q q q q q q q q
q q
q q
20
20
q q q q
q q q q
q q
q q
q q q q
q q
q q
0
0
5 10 15 20 25 5 10 15 20 25
vitesse du véhicule vitesse du véhicule
De l’histogramme au regressogramme
104

105. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Naturellement, on peut consid´rer un r´gressogramme glissant,
e e
n
Yi 1(Xi ∈ [xh ; x + h])
i=1
ϕ(x) = n pour tout x,
1(Xi ∈ [xh ; x + h])
i=1
o` h > 0.
u
105

106. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
120
120
q q
100
100
q
q q
q
q q q q
distance de freinage
distance de freinage
80
80
q q
q q
q q
q q
q q
q q
60
60
q q
q q q q
q q q q
q q
q q
q q
q q q q
q q
40
40
q q q q
q q q q
q q q q
q q q q q q
q q q q
q q q q q q q q
q q
q q
20
20
q q q q
q q q q
q q
q q
q q q q
q q
q q
0
0
5 10 15 20 25 5 10 15 20 25
vitesse du véhicule vitesse du véhicule
106

107. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
De l’histogramme au regressogramme
Notons qu’on peut ´galement obtenir un intervalle de confiance, soit en utilisant
e
un intervalle de confiance gaussien (avec l’´cart-type estim´ sur le voisinage, -) ou
e e
en utilisant les quantiles empiriques (-).
120
120
q q
100
100
q
q q
q
q q q q
distance de freinage
distance de freinage
80
80
q q
q q
q q
q q
q q
q q
60
60
q q
q q q q
q q q q
q q
q q
q q
q q q q
q q
40
40
q q q q
q q q q
q q q q
q q q q q q
q q q q
q q q q q q q q
q q
q q
20
20
q q q q
q q q q
q q
q q
q q q q
q q
q q
0
0
5 10 15 20 25 5 10 15 20 25
vitesse du véhicule vitesse du véhicule
107

108. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
De l’histogramme au regressogramme
Nous venons de prendre la moyenne sur les voisins de x distants d’au plus ±h.
Une autre id´e peut ˆtre de chercher les k plus proches voisins
e e
n
Yi 1(Xi ∈ Vx )
i=1
ϕ(x) = n pour tout x,
1(Xi ∈ Vx )
i=1
o` Vx contient les k plus proches voisins de x.
u
108

109. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
120
120
q q
100
100
q
q q
q
q q q q
distance de freinage
distance de freinage
80
80
q q
q q
q q
q q
q q
q q
60
60
q q
q q q q
q q q q
q q
q q
q q
q q q q
q q
40
40
q q q q
q q q q
q q q q
q q q q q q
q q q q
q q q q q q q q
q q
q q
20
20
q q q q
q q q q
q q
q q
q q q q
q q
q q
0
0
5 10 15 20 25 5 10 15 20 25
vitesse du véhicule vitesse du véhicule
109

110. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
De l’histogramme au regressogramme
Lai (1977) a montr´ la convergence de cet estimateur
e
Proposition 1. Si k → ∞, k/n → 0 alors
ϕ (x) k 2
E(ϕk (x)) ∼ ϕ(x) +
8 n2
et
2σ 2 (x)
V ar(ϕk (x)) ∼ .
k
Aussi, en faisant un compromis entre biais et variance conduit ` retenir k ≈ n4/5 .
a
Sur notre exemple, n = 50 et k = 22.
110

111. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
La r´gression locale
e
L’id´e est ici simplement de consid´rer le voisinage en terme de nombre de
e e
voisines.
> loess(dist ~ speed, cars,span=0.75,degree=2)
> predict(REG, data.frame(speed = seq(5, 25, 0.25)), se = TRUE)
Le param`tre span correpond au pourcentage de points gard´s pour faire
e e
l’ajustement local, et degree est le typoe de r´gression polynomiale.
e
111

112. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
La r´gression locale, m´thode lowess
e e
Ici ajustement local au voisinage de x = 15, avec 25% de points pour d´finir le
e
voisinage (on garde 25% des points les plus proches, en x), et un ajustement
lin´ire.
a
120
120
q q
100
100
q
q q
q
q q q q
Distance de freinage
Distance de freinage
80
80
q q
q q
q q
q q
q q
q q
60
60
q q
q q q q
q q q q
q q
q q
q q q
q q q q
q q
40
40
q q q q q
q q q q
q q q q
q q q q q q q
q q q q
q q q q q q q q
q q
q q
20
20
q q q q
q q q q
q q
q q
q q q q
q q
q q
0
0
5 10 15 20 25 5 10 15 20 25
Vitesse du véhciule Vitesse du véhciule
112

113. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
La r´gression locale, m´thode lowess
e e
Ici ajustement local au voisinage de x = 15, avec 50% de points pour d´finir le
e
voisinage (on garde 50% des points les plus proches, en x), et un ajustement
lin´ire.
a
120
120
q q
100
100
q
q q
q
q q q q
Distance de freinage
Distance de freinage
80
80
q q
q q
q q
q q
q q
q q
60
60
q q
q q q q
q q q q
q q
q q
q q q
q q q q
q q
40
40
q q q q q
q q q q q
q q q q
q q q q q q
q q q q
q q q q q q q q
q q
q q
20
20
q q q q
q q q q
q q
q q
q q q q
q q
q q
0
0
5 10 15 20 25 5 10 15 20 25
Vitesse du véhciule Vitesse du véhciule
113

114. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
La r´gression locale, m´thode lowess
e e
Ici ajustement local au voisinage de x = 14, avec 75% de points pour d´finir le
e
voisinage (on garde 75% des points les plus proches, en x), et un ajustement
lin´ire.
a
120
120
q q
100
100
q
q q
q
q q q q
Distance de freinage
Distance de freinage
80
80
q q
q q
q q
q q
q q
q q
60
60
q q
q q q q
q q q q
q q
q q
q q
q q q q
q q
40
40
q q q q q
q q q q
q q q q
q q q q q q q
q q q q
q q q q q q q q
q q
q q
20
20
q q q q
q q q q
q q
q q
q q q q
q q
q q
0
0
5 10 15 20 25 5 10 15 20 25
Vitesse du véhciule Vitesse du véhciule
114

115. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
La r´gression locale, m´thode lowess
e e
Ici ajustement local au voisinage de x = 17, avec 35% de points pour d´finir le
e
voisinage (on garde 35% des points les plus proches, en x), et un ajustement
quadratique.
120
120
q q
100
100
q
q q
q
q q q q
Distance de freinage
Distance de freinage
80
80
q q
q q
q q
q q
q q
q q
60
60
q q q
q q q q
q q q q
q q
q q
q q q
q q q q
q q
40
40
q q q q
q q q q q
q q q q
q q q q q q
q q q q
q q q q q q q q
q q
q q
20
20
q q q q
q q q q
q q
q q
q q q q
q q
q q
0
0
5 10 15 20 25 5 10 15 20 25
Vitesse du véhciule Vitesse du véhciule
115

116. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
La r´gression locale, m´thode lowess
e e
Ici ajustement local au voisinage de x = 11, avec 75% de points pour d´finir le
e
voisinage (on garde 35% des points les plus proches, en x), et un ajustement
quadratique.
120
120
q q
100
100
q
q q
q
q q q q
Distance de freinage
Distance de freinage
80
80
q q
q q
q q
q q
q q
q q
60
60
q q
q q q q
q q q q
q q
q q
q q
q q q q
q q
40
40
q q q q
q q q q
q q q q
q q q q q q q
q q q q
q q q q q q q q q
q q
q q
20
20
q q q q q
q q q q
q q
q q
q q q q
q q
q q
0
0
5 10 15 20 25 5 10 15 20 25
Vitesse du véhciule Vitesse du véhciule
116

117. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Du lin´aire au nonlin´aire, une vision g´n´ale
e e e r
Dans le cas lin´aire, nous avions not´ que
e e
Y = Y − X β = X(X X)−1 X Y
H
o` H peut ˆtre interpr´t´e comme une matrice de lissage. Notons que
u e ee
n n
Yj = [X j (X X)−1 X ]i Yi = [H(X j )]i Yi
i=1 i=1
o` H(x) = x (X X)−1 X .
u
Aussi, ´tant donn´e une nouvelle observation x = (x1 , · · · , xk ),
e e
n
E(Y |X = x) = [H(x)]i Yi = Y (x).
i=1
117

118. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Un estimateur sans biais de σ 2 = V ar(εi ) est alors simplement
n
2 1
σ = (Yi − Yi )2 .
n−k i=1
On en d´duit alors simplement un intervalle de confiance pour Y sachant X = x,
e
de la forme
n
Y (x) ± zσ 2 H(x) 2
, o` H(x)
u 2
= (H(x)i )2
i=1
Definition 2. Un pr´dicteur Y (x) sera dit dit lin´aire s’il pour tout x, il existe
e e
un vecteur S(x) = (S(x)1 , · · · , S(x)n ) tel que
n
Y (x) = S(x)i Yi
i=1
Definition 3. Si [Y (X)i ] d´sine le vecteur Y1 , · · · , Yn . Il est alors possible
e
d’´crire [Y (X)i ] = SY, o` S est une matrice n × n.
e u
Dans le cas du mod`le lin´aire S = H.
e e
118

119. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
Examples de matrices de lissage S
Consid´rons le cas d’un moyenne glissante, i.e. on fait une moyenne locale sur les
e
points distants (au plus d’une distance h = 1).
Sur les 9 observations suivantes,
Xi 1 2 3 4 5 6 7 8 9
Yi 5 3 1 7 6 5 2 1 6
Alors n
i=1 Yi × 1(|Xi − x| ≤ 1)
Y (x) = n ,
i=1 1(|Xi − x| ≤ 1)
119

120. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
et  
1/2 1/2 0 0 0 0 0 0 0
 
 1/3 1/3 1/3 0 0 0 0 0 0 
 
 
 0 1/3 1/3 1/3 0 0 0 0 0 
 
Sh=1 = 0 0 1/3 1/3 1/3 0 0 0 0 
 
 
 ... ... ... ... ... ... ... ... ... 
 
 
 0 0 0 0 0 0 1/3 1/3 1/3 
 
0 0 0 0 0 0 0 1/2 1/2
120

121. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
To go further (the theory)
121

122. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
To go further (the applications)
122

123. ` ´
Arthur CHARPENTIER - Moddeles de previsions (ACT6420 - Automne 2012)
123