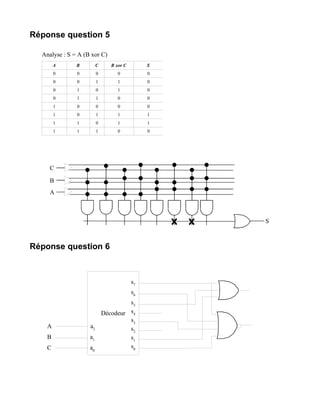
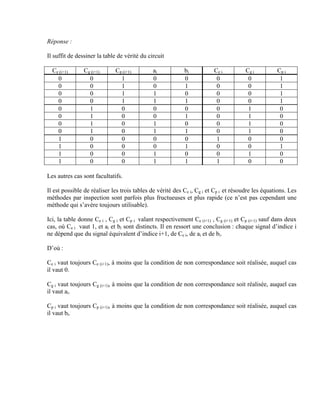
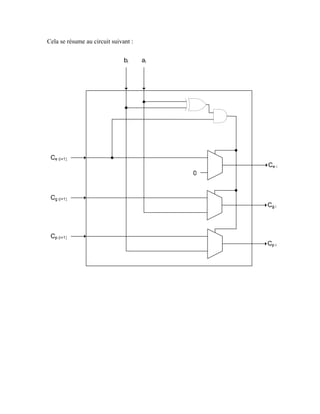
Le document contient des réponses à une série de questions sur la conception de circuits logiques, abordant des sujets tels que les portes logiques, les multiplexeurs, et les décodeurs. Il décrit également la création de systèmes de contrôle pour des missiles intercontinentaux, des additionneurs BCD, ainsi que des méthodes de simplification de circuits logiques. Enfin, des équations et des schémas sont présentés pour illustrer les principes discutés.

1. Réponse question 1
A[3..0] B[3..0]
b a 1
= 0 1
E4 E0
G4 Comp. Comp. Comp. Comp. G0
P4 1-bit 1-bit 1-bit 1-bit P0
0 1 0 1 0 1 0 1
0 1 0 1 0 1 0 1
S0 S1 S2 S3
Réponse question 2
Pour obtenir l'équivalent d'une porte logique avec un multiplexeur, il suffit d'utiliser la méthode de
table de Karnaug à table inscrite et d'inscrire une des deux entrées :
OU ET
XOR
0 1 A B S S (B A B S S (B
1 XOR inscrit) inscrit)
0
1 1
0 0 0 0 B 0 0 0 0
a 0 0
1 1 s 0 1 1 0 1 0
b 0
1 0 1 1 1 0 0 B
ri-1
1 1 1 1 1 1
1
0 0 OU
1 1 r
ET 0 XOR
ET Pour réaliser le XOR,
A B S S (B
1 inscrit) puisqu'une valeur
0 0 0 0 0 B inscrite est inversée, il
0 1 1 faut également utiliser
1 0 1 B' un multiplexeur pour
créer un inverseur
1 1 0

2. Réponse question 3
A[3..0] B[3..0]
b a
E4 E0
G4 Comp. Comp. Comp. Comp. G0
P4 1-bit 1-bit 1-bit 1-bit P0
r4 Σ Σ Σ Σ r0
1-bit 1-bit 1-bit 1-bit
S3 S2 S1 S0
Réponse question 4
SD1 e3
e3
s1
s1
SD2 e2
e2 Encodeur 3
s0
s0 2 O[1]
e1 Priorité 1
SD3 e1
0 0
0 e0
e0
S1[1]
S1[0] 3
2 O[0]
S2[1] 1
0 0
S2[0]
S3[1] Partie b)
S3[0] s3 A1
e1 s2 A2
Demux
s1 A3
e0
s0

3. Réponse question 5
Analyse : S = A (B xor C)
A B C B xor C S
0 0 0 0 0
0 0 1 1 0
0 1 0 1 0
0 1 1 0 0
1 0 0 0 0
1 0 1 1 1
1 1 0 1 1
1 1 1 0 0
C
B
A
S
Réponse question 6
s7
s6
s5
Décodeur s4
s3
A a2 s2
B a1 s1
C a0 s0

4. Réponse question 7
Vous êtes chargé de concevoir le circuit de contrôle pour une système de missiles intercontinentales
(ICBMs). Il-y-a 16 missiles à contrôler. Quand une missile reçoit logique-1, elle est envoyée vers son
cible. L'interface usager consiste de deux entrées. Il-y-a un sélectionneur de missile/cible qui sort un
code binaire de 4-bits, et il-y-a un gros bouton rouge qui sort logique-1 quand c'est dépressé.
Évidemment, quand un général de quatres étoiles dépresse le bouton, le missile sélectionnée devrait
être lancé.
a) Implémentez ce système en n'utilisant que cinq démultiplexeurs 1x4 (c'est a dire des DEMUX à
quatres sorties).
b) Implémentez ce système en utilisant des portes logiques, mais assurez vous que le système n'a pas
d'aléas ! (Aléa c'est le chapitre 3.6, donc ce n'est pas à l'examen)
C'est possible de remplir une table de vérité avec 32 entrées, mais, c'est plus facile de constater qu'une
missile n'est lancé qu'à une seule condition (une seule minterme) : il faut que le missile soit
sélectionnée, et que le bouton rouge soit dépressé. Ça fait que le système n'est que 16 portes ET à 5
entrées et des inverseurs. Par exemple pour la dixième missile c'est :
Est-ce-qu'il-y-a des aléas ? Non, parce que chaque sous-circuit n'a qu'une seule minterme. Alors il n'y
a pas de risque que nos missiles se lancent par accident.

5. Réponse question 8
Concevez un décodeur qui transforme le code Gray en ASCII. C'est a dire que ça transforme (0000)2 à
(1000000)2, (0001)2 à (1000001)2, etc... Pour les codes de Gray qui représentent de 10 à 15 en binaire,
ça doit sortir les lettres majuscules de A à F en ASCII. Vous pouvez trouver une table de codes ASCII
dans votre texte (p. 47) ou sur www.asciitable.com. Le code de Gray se retrouve sur p. 45.
Comme première étape, c'est souhaitable de remplir la table de vérité :
Entrée Sortie Et, comme deuxième étape il faut la simplifier. Vous pouvez utiliser
(Gray) (ASCII) 7 tables de Karnaugh à 4 variables. Vous pouvez aussi inscrire le bit
le plus significatif du code Gray pour simplifier les tables de
0000 0110000 Karnaugh. Vous pouvez faire un simplification hybride en utilisant
0001 0110001 des MUX pour les 3 bits les plus significatifs de la sortie (parce-qu'ils
0010 0110011 se repètent souvent). Et il-y-a toujours l'algèbre et la méthode Quine-
McCluskey...
0011 0110010
Jeff conseille de simplifier avec des MUX pour les 3 bits les plus
0100 0110111 significatifs et avec les tables de Karnaugh pour les autres trois bits.
0101 0110110 Utilisez des variables inscrites où ça aide beaucoup à simplifier.
Comme ça vous allez bien apprendre trois méthodes de simplification
0110 0110100 pour l'intra. :-)
0111 0110101
1000 1000110
1001 1000101
1010 1000011
1011 1000100
1100 0111000
1101 0111001
1110 1000010
1111 1000001

6. Réponse question 9
Implémentez la fonction suivante en ne se servant que d'un MUX 2x1 (vous avez droit aux entrées et
leurs inverses) :
a b c s
0 0 0 1
0 0 1 1
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 0
1 1 0 0
1 1 1 1
Réponse question 10
Transformez l'additionneur suivant en additionneur/soustracteur en n'utilisant que 4 portes OU-exclusif
(OUX) à deux entrées. Créez une entrée supplémentaire qui s'appelle Add/Sub : quand cette entrée est
logique-0, le circuit devrait faire l'addition, et quand c'est logique-1, le circuit devrait faire le
soustraction. N'oubliez pas que soustraire c'est la même chose que additionner – mais avec le
complément à deux d'une terme. N'oubliez pas que faire le complément à deux ne prend que deux
étapes façiles à implémenter en circuits logiques !

7. Question 11
Un additionneur "itératif" BCD
Soient A et B deux mots de 4 bits. Supposons que A et B représentent les chiffres de 0 à 9 selon la
convention du code BCD 8421, telle que présentée à la table ci-dessous :
Chiffre Représentation
0 0000
1 0001
2 0010
3 0011
4 0100
5 0101
6 0110
7 0111
8 1000
9 1001
Tableau 11.1.a, code BCD 8421
Nous allons concevoir un circuit permettant l’addition des mots A et B de quatre bits (a3a2a1a0 et
b3b2b1b0 respectivement) et de produire un résultat sur 5 bit, où les quatre bits les moins
significatifs représenteront le mot K (k3k2k1k0) résultant de l’addition, et le dernier représentera la
retenue, notée y. Les nombres A, B et K sont en format BCD.
Tel que présenté au tableau suivant. Notons que les mots A, B et K sont représentés en BCD:
A+B=K 0 1 2 3 4 5 6 7 8 9
0 0 1 2 3 4 5 6 7 8 9
1 1 2 3 4 5 6 7 8 9 0
2 2 3 4 5 6 7 8 9 0 1
3 3 4 5 6 7 8 9 0 1 2
4 4 5 6 7 8 9 0 1 2 3
5 5 6 7 8 9 0 1 2 3 4
6 6 7 8 9 0 1 2 3 4 5
7 7 8 9 0 1 2 3 4 5 6
8 8 9 0 1 2 3 4 5 6 7
9 9 0 1 2 3 4 5 6 7 8
Tableau 11.1.b, Addition A+B=C en chiffres (C est représenté en format BCD)
A+B=>r 0 1 2 3 4 5 6 7 8 9
0 0 0 0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0 0 0 1
2 0 0 0 0 0 0 0 0 1 1
3 0 0 0 0 0 0 0 1 1 1
4 0 0 0 0 0 0 1 1 1 1
5 0 0 0 0 0 1 1 1 1 1
6 0 0 0 0 1 1 1 1 1 1
7 0 0 0 1 1 1 1 1 1 1
8 0 0 1 1 1 1 1 1 1 1
9 0 1 1 1 1 1 1 1 1 1
Tableau 11.1.c, Obtention de la retenue pour l’addition de A et B

8. Il serait illusoire d’essayer de dessiner une table de vérité pour l’ensemble de ces cas (il y en a 100,
et si nous considérions la symétrie de A et B, il en resterait quand même 55).
Nous allons plutôt procéder en utilisant des circuits usuels. Supposons que nous additionnions les
nombres A et B avec un additionneur 4 bits dont voici le schéma général1 :
Fig 11.1.a additionneur générique
Où C est le résultat de l’addition sur 4 bits (c3c2c1c0), et r la retenue. Cette addition ne représente
pas le nombre C en format BCD, mais elle permet de simplifier le traitement. Il suffit en effet
d’ajouter un circuit qui convertit les cinq signaux r, c3, c2, c1 et c0 en y, k3, k2, k1 et k0. Ce circuit à
concevoir peut être schématisé par le bloc représentatif suivant :
r C
4
Convertisseur BCD avec retenue
4
y K
Fig 11.1.b circuit de conversion BCD avec retenue
1
Lorsqu’une entrée ou sortie présente une barre, celle-ci signifie qu’il s’agit d’un ensemble de fils (souvent appelé
bus) dont le nombre est écrit à côté.

9. 11.1) Dessinez la table de vérité associant les entrées C et r aux entrées K et y (cinq bits de chaque
côté de la table)
Réponse :
r c3 c2 c1 c0 y k3 k2 k1 k0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 1 0 0 0 0 1
0 0 0 1 0 0 0 0 1 0
0 0 0 1 1 0 0 0 1 1
0 0 1 0 0 0 0 1 0 0
0 0 1 0 1 0 0 1 0 1
0 0 1 1 0 0 0 1 1 0
0 0 1 1 1 0 0 1 1 1
0 1 0 0 0 0 1 0 0 0
0 1 0 0 1 0 1 0 0 1
0 1 0 1 0 1 0 0 0 1
0 1 0 1 1 1 0 0 1 0
0 1 1 0 0 1 0 0 1 1
0 1 1 0 1 1 0 1 0 0
0 1 1 1 0 1 0 1 0 1
0 1 1 1 1 1 0 1 1 0
1 0 0 0 0 1 0 1 1 1
1 0 0 0 1 1 1 0 0 0
1 0 0 1 0 1 1 0 0 1
1 0 0 1 1 1 0 0 0 1
1 0 1 - - - - - - -
1 1 - - - - - - - -
Tableau 3.1.s.a, Obtention de la retenue pour l’addition de A et B
1.2) Que pouvez vous dire des cas où le résultat y vaut 0?
Réponse :
r = y, C = K
11.3) Que pouvez-vous dire lorsque y vaut 1 (indice : il suffit d’ajouter une constante à C)
Réponse :
Il suffit d’ajouter la constante 6 (0110) à C pour obtenir y et K

10. 11.4) Trouvez l’équation (en produit de sommes) donnant y en fonction des bits de C et r (note y
est indépendant de c0):
Réponse :
Puisque y est indépendant de c0, il suffit d’écrire une table de Karnaugh à 4 variables (r, c3, c2, c1).
y c2c1
00 01 10 11
00 0 0 0 0
01 0 1 1 1
rc3
11 - - - -
10 1 1 - -
y = (r+c3)(r+c2+c1)
11.5) A l’aide de tout ce qui précède, réalisez le circuit de la figure 3.1.b
Réponse :
Fig 11.s.a Solution 3.1.5

11. Question 12
Comparateur itératif à rebours
Nous avons présenté dans le cours la conception d’un comparateur de deux mots de 4 bits
représentant des entiers binaires. En suivant la même démarche que celle du cours, réalisez un
comparateur avec des cellules qui comparent à rebours, de sorte que votre circuit respecte le
schéma suivant :
Sachant que ce circuits est constitué des 4 cellules itératives suivant ce schéma :
Où les Ce i , Cg i et Cp i sont des signaux pour encoder la réponse de l’étage i respectant les trois cas
présentés à la table suivante :
Signification Cei Cgi Cpi
Égalité 1 0 0
A plus grand que B 0 1 0
A plus petit que B 0 0 1
La combinaison des trois signaux ne peut prendre d’autre valeur.
Notons finalement que Ce4, Cg4 et Cp4 valent respectivement 1, 0 et 0.
Essayez de répondre sans utiliser aucune table de Karnaugh (note : il est possible d’utiliser un mux
à 2 entrées et 1 signal de contrôle) ?

12. Réponse :
Il suffit de dessiner la table de vérité du circuit
Ce (i+1) Cg (i+1) Cp (i+1) ai bi Ce i Cg i Cp i
0 0 1 0 0 0 0 1
0 0 1 0 1 0 0 1
0 0 1 1 0 0 0 1
0 0 1 1 1 0 0 1
0 1 0 0 0 0 1 0
0 1 0 0 1 0 1 0
0 1 0 1 0 0 1 0
0 1 0 1 1 0 1 0
1 0 0 0 0 1 0 0
1 0 0 0 1 0 0 1
1 0 0 1 0 0 1 0
1 0 0 1 1 1 0 0
Les autres cas sont facultatifs.
Il est possible de réaliser les trois tables de vérité des Ce i, Cg i et Cp i et résoudre les équations. Les
méthodes par inspection sont parfois plus fructueuses et plus rapide (ce n’est pas cependant une
méthode qui s’avère toujours utilisable).
Ici, la table donne Ce i , Cg i et Cp i valant respectivement Ce (i+1) , Cg (i+1) et Cp (i+1) sauf dans deux
cas, où Ce i vaut 1, et ai et bi sont distincts. Il en ressort une conclusion : chaque signal d’indice i
ne dépend que du signal équivalent d’indice i+1, de Ce i, de ai et de bi.
D’où :
Ce i vaut toujours Ce (i+1), à moins que la condition de non correspondance soit réalisée, auquel cas
il vaut 0.
Cg i vaut toujours Cg (i+1), à moins que la condition de non correspondance soit réalisée, auquel cas
il vaut ai.
Cp i vaut toujours Cp (i+1), à moins que la condition de non correspondance soit réalisée, auquel cas
il vaut bi.

13. Cela se résume au circuit suivant :

14. Question 13
Additionneur 4 bits
Expliquer pourquoi le XOR (dont la sortie est notée d) se trouvant à la fin du circuit d'addition
suivant sert à la détection du débordement :
⎧0 , addition
c=⎨
⎩1 , soustraction
bn-1 b2 b1 b0
an-1 a2 a1 a0
rn-1 r3 r2 r1
Σ Σ Σ Σ
r0
rn sn-1 s2 s1 s0
d
détection de débordement
Réponse :
Le débordement survient dans deux cas uniquement, lorsque l’addition de deux nombres négatifs
donne un nombre positif, ou celle de deux nombres négatifs donne un nombre positif. Cela
correspond à avoir les retenues rn-1 et rn distincts. Autrement (cas de non débordement), rn-1 et rn
sont toujours semblables. Un XOR peut donc effectuer la détection de débordement si il a pour
entrée rn-1 et rn.