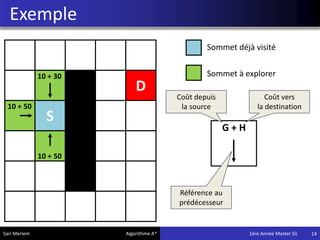
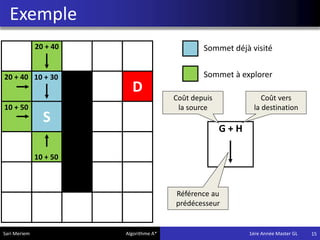
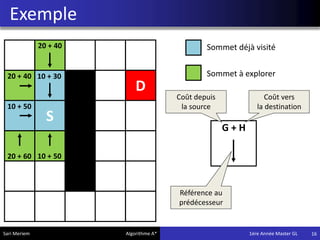
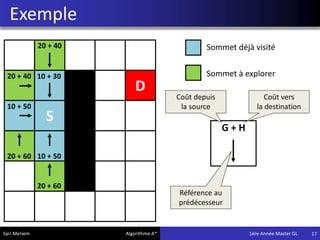
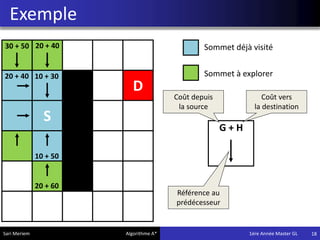
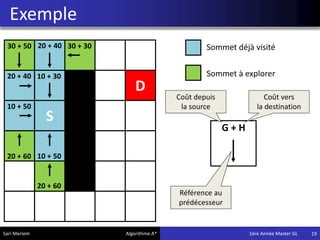
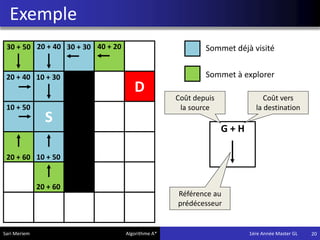
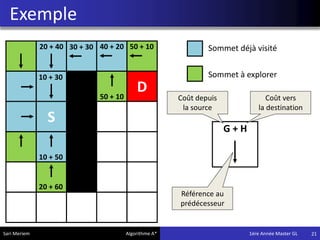
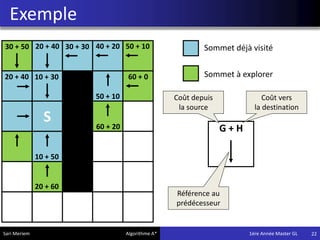
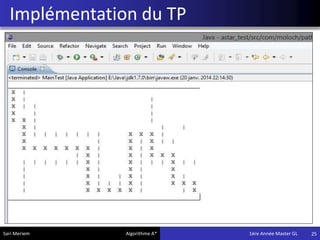
L'algorithme A* est une méthode de pathfinding développée en 1968 qui permet de trouver un chemin optimal entre une source et une destination dans un graphe. Bien qu'il ne garantisse pas toujours la solution la plus optimale, il offre des résultats rapides, ce qui le rend utile dans divers domaines comme les jeux vidéo et la simulation. Son implémentation repose sur des classes spécifiques qui gèrent les noeuds et les calculs de coûts associés.

1. Algorithme A*
Par: Sari Meriem
1
UNIVERSITE MOHAMED CHERIF MESAADIA
SOUK-AHRAS
Exposé sur:

2. Plan
2
 Introduction.
 Algorithme A star.
 Objectif.
 Applications.
 Description.
 Algorithme.
 Exemple.
 Implémentation du TP.
 Conclusion.
Sari Meriem Algorithme A* 1ére Année Master GL

3. Introduction
3
 Le « PATHFINDING » est un domaine de l'informatique qui étudie
les différentes façons de trouver un chemin entre un point A et un
point B.
 L'un des algorithmes de pathfinding les plus connus est A* (
prononcez A étoile, ou A star en anglais).
Sari Meriem Algorithme A* 1ére Année Master GL

4. Introduction
4
C’est quoi le A *?
Sari Meriem Algorithme A* 1ére Année Master GL

5. A star
5
 A été proposé pour la première fois par Peter E. Hart, Nils Nilsson
et Bertram Raphael en 1968.
 Est une extension de l'algorithme de Dijkstra de 1959.
 Est un algorithme itératif.
 Permet la recherche d’un chemin à partir d’un état Initial (source)
vers un état final (destination).
 Il ne donne pas toujours la solution optimale mais il donne très
rapidement une bonne solution.
Sari Meriem Algorithme A* 1ére Année Master GL

6. Objectif
6
 Déterminer, pour un agent donné, un chemin de coût minimum
depuis un sommet source vers un sommet destination au sein d’un
graphe.
 Un agent est un objet informatique utilisé pour représenter une
entité mobile dotée d’un comportement (humain, animal, véhicule,
…)
Sari Meriem Algorithme A* 1ére Année Master GL

7. Objectif
7
 Le coût d’un arc dépend de l’application de l’algorithme.
 Exemple:
 Distance kilométrique:
Recherche de chemins de longueur minimale.
 Temps:
Recherche de chemins en temps minimum.
 Consommation de carburant:
Rechercher de chemins « économes ».
Sari Meriem Algorithme A* 1ére Année Master GL

8. Applications
8
 Jeux vidéo:
 Animation des personnages non joueurs.
 Déplacement réaliste d’un personnage contrôlé par le joueur
vers un objectif désigné par le joueur.
 Simulation – vie artificielle:
 Etude du comportement d’une foule, du trafic automobile, …
 Effets spéciaux (scènes de bataille, …)
Sari Meriem Algorithme A* 1ére Année Master GL

9. Description
9
 Vocabulaires nécessaire à savoir:
 Le graphe: ensemble des nœuds et des arcs.
 Un nœud: c'est une unité du graphe, l'algorithme va parcourir le
graphe en passant des nœuds.
 La liste ouverte: C'est une liste qui contient les nœuds à analyser.
 La liste fermée: C'est une liste qui contient les nœuds déjà
analysés.
Sari Meriem Algorithme A* 1ére Année Master GL

10. Description
10
 Pour chaque nœuds on a les propriétés suivante:
 Parent (P): il s'agit du prédécesseur du nœud courant.
 G: il s'agit de la distance parcourue depuis le point de départ pour
arriver au nœud courant (Coût depuis la source).
 H: il s'agit de la distance à vol d'oiseau entre le nœud courant et le
nœud d'arrivée (Coût vers la destination).
 Poids(F): Coût depuis la source (G) + Coût vers la destination (H) .
Sari Meriem Algorithme A* 1ére Année Master GL

11. Algorithme
11
Initialisation
Sommet source (S)
Sommet destination (D)
Liste ouverte à explorer (E) : sommet source S
Liste fermée déjà visités (V) : vide
Tant que (la liste E est non vide) et (D n’est pas dans E) Faire
+ Récupérer le sommet X de coût F minimum.
+ Ajouter X à la liste V
+ Ajouter les successeurs de X (non déjà visités) à la liste E en
évaluant leur coût F et en identifiant leur prédécesseur.
+ Si (un successeur est déjà présent dans E) et
(nouveau coût est inférieur à l’ancien) Alors
Changer son coût F
Changer son prédécesseur
FinSi
FinFaire
Sari Meriem Algorithme A* 1ére Année Master GL

12. Algorithme
12
 L’algorithme s’ arrêtera dans deux cas:
I. Si la liste des nœuds à visiter (ouverte) est vide et le nœud
destinations n’appartient pas à la liste des nœuds déjà visité
(fermée)  dans ce cas il n’y a pas de chemin entre la source et
la destination.
II. Si le nœud destination appartient à la liste des nœuds déjà
visité (fermée)  dans ce cas l’algorithme a trouvé un chemin
entre la source et la destination.
Sari Meriem Algorithme A* 1ére Année Master GL

13. Exemple
13
S
D
S
D
Sommet source
Sommet destination
Obstacle
Sari Meriem Algorithme A* 1ére Année Master GL

14. Exemple
14
S
D
10 + 30
10 + 50
10 + 50
Sommet déjà visité
Sommet à explorer
G + H
Coût depuis
la source
Coût vers
la destination
Référence au
prédécesseur
Sari Meriem Algorithme A* 1ére Année Master GL

15. Exemple
15
S
D
10 + 30
10 + 50
10 + 50
20 + 40
20 + 40 Sommet déjà visité
Sommet à explorer
G + H
Coût depuis
la source
Coût vers
la destination
Référence au
prédécesseur
Sari Meriem Algorithme A* 1ére Année Master GL

16. Exemple
16
S
D
10 + 30
10 + 50
10 + 50
20 + 40
20 + 40
20 + 60
Sommet déjà visité
Sommet à explorer
G + H
Coût depuis
la source
Coût vers
la destination
Référence au
prédécesseur
Sari Meriem Algorithme A* 1ére Année Master GL

17. Exemple
17
S
D
10 + 30
10 + 50
10 + 50
20 + 40
20 + 40
20 + 60
20 + 60
Sommet déjà visité
Sommet à explorer
G + H
Coût depuis
la source
Coût vers
la destination
Référence au
prédécesseur
Sari Meriem Algorithme A* 1ére Année Master GL

18. Exemple
18
S
D
10 + 30
10 + 50
20 + 40
20 + 40
20 + 60
30 + 50 Sommet déjà visité
Sommet à explorer
G + H
Coût depuis
la source
Coût vers
la destination
Référence au
prédécesseur
Sari Meriem Algorithme A* 1ére Année Master GL

19. Exemple
19
S
D
10 + 30
10 + 50
10 + 50
20 + 40
20 + 40
20 + 60
20 + 60
30 + 50 30 + 30 Sommet déjà visité
Sommet à explorer
G + H
Coût depuis
la source
Coût vers
la destination
Référence au
prédécesseur
Sari Meriem Algorithme A* 1ére Année Master GL

20. Exemple
20
S
D
10 + 30
10 + 50
10 + 50
20 + 40
20 + 40
20 + 60
20 + 60
30 + 50 30 + 30 40 + 20 Sommet déjà visité
Sommet à explorer
G + H
Coût depuis
la source
Coût vers
la destination
Référence au
prédécesseur
Sari Meriem Algorithme A* 1ére Année Master GL

21. Exemple
21
S
D
10 + 30
10 + 50
20 + 40
20 + 60
30 + 30 40 + 20 50 + 10
50 + 10
Sommet déjà visité
Sommet à explorer
G + H
Coût depuis
la source
Coût vers
la destination
Référence au
prédécesseur
Sari Meriem Algorithme A* 1ére Année Master GL

22. Exemple
22
S
10 + 30
10 + 50
20 + 40
20 + 40
20 + 60
30 + 50 30 + 30 40 + 20 50 + 10
50 + 10
60 + 20
60 + 0
Sommet déjà visité
Sommet à explorer
G + H
Coût depuis
la source
Coût vers
la destination
Référence au
prédécesseur
Sari Meriem Algorithme A* 1ére Année Master GL

23. Exemple
23
S
D
Sari Meriem Algorithme A* 1ére Année Master GL

24. Implémentation du TP
24
 L'implémentation proposée se base sur 4 classes :
 Astar: une classe fournissant l'algorithme de calcul.
 Node: une classe représentant un noeud du parcours .
 NodeFactory: une classe abstraite permettant de créer les
noeuds, dans laquelle il faut implémenter les méthodes de calcul
de G et H.
 SuccessorComputer: une classe abstraite fournissant les
successeurs d'un point particulier.
 MainTest: une classe fournissant un cas de test concret sur une
chaine de caractères ou " " représente un chemin exploitable et
" | " représente un chemin interdit.
Sari Meriem Algorithme A* 1ére Année Master GL

25. Implémentation du TP
25Sari Meriem Algorithme A* 1ére Année Master GL

26. Conclusion
26
 L’algorithme A* ne donne pas toujours la meilleure solution mais il
en donne une bonne solution.
 On pourrait comparer ses performances avec celles de
l'algorithme de Dijkstra.
 Dijkstra donne la meilleure solution, mais A* est plus rapide.
Sari Meriem Algorithme A* 1ére Année Master GL