cours de complexité algorithmique

Enseignants: Dr. Atef MASMOUDI & Dr. Ameur CH’HAYDER
AU: 2015-2016
17/12/2015 1Dr. Atef MASMOUDI & Dr. Ameur CH'HAYDER, IPEIS, AU:2015-2016
https://www.facebook.com/groups/informatique.prepas

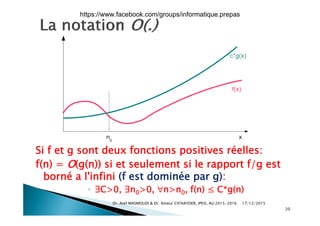
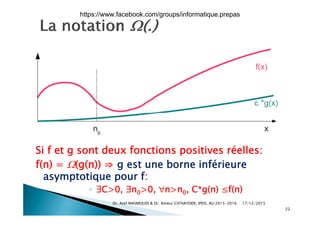
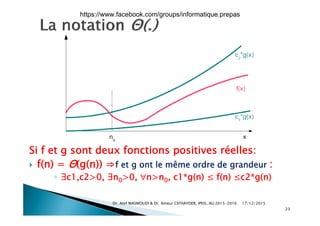
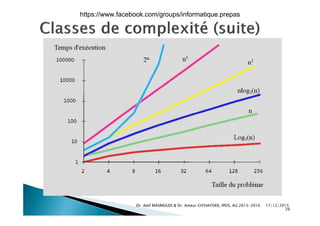
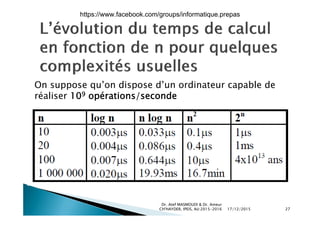
L thé i d l l ité l ith i i à La théorie de la complexité algorithmique vise à:
◦ classer les problèmes selon leur difficulté,
classer les algorithmes selon leur efficacité◦ classer les algorithmes selon leur efficacité,
◦ comparer les algorithmes résolvant un même problème.
Proposer en Python deux programmes différentsProposer en Python deux programmes différents
pour vérifier la primalité d’un entier n?
Proposer en Python deux programmes différents
pour calculer xn?pour calculer xn?
17/12/2015Dr. Atef MASMOUDI & Dr. Ameur CH'HAYDER, IPEIS, AU:2015-2016
2

 Pour mesurer le temps d'exécution d’un programme en
Python nous pouvons simuler un chronomètre :
◦ on le déclenche juste avant le début du programmeon le déclenche juste avant le début du programme,
◦ on l'arrête juste après la fin du programme,
◦ le temps écoulé entre les deux pressions est la durée qui nous
intéresse.
 En Python, on peut simuler un chronomètre grâce au
module time ;
Exemple:
f i i *from time import *
debut = time() # on déclenche le chronomètre
# votre programmeot e p og a e
fin = time() # on arrête le chronomètre
print(’Temps écoulé:’, fin - debut, ’ secondes’)
3

Ecrire un programme Python pour vérifier la
i lité d ?primalité de n?
Programme naïf: vérifier si n possède un diviseur dans
l’intervalle [2,n-1]
17/12/2015Dr. Atef MASMOUDI & Dr. Ameur CH'HAYDER, IPEIS, AU:2015-2016 4

Ecrire un programme Python pour vérifier la
primalité de n?primalité de n?
Programme rapide: vérifier si n possède un diviseur dans
l’intervalle [2 n]l intervalle [2,n],
5

Ecrire un programme Python pour calculer xn?
Méthode classique:
Xn x*x* *xXn=x*x*………….*x
n foisn fois
17/12/2015
6
Dr. Atef MASMOUDI & Dr. Ameur CH'HAYDER, IPEIS, AU:2015-2016

Exponentiation rapide
17/12/2015 7Dr. Atef MASMOUDI & Dr. Ameur CH'HAYDER, IPEIS, AU:2015-2016

D l’ét d d l ité d’ l ithDans l’étude de complexité d’un algorithme on ne mesure pas
la durée en heures, minutes, secondes, ...:
◦ cela impliquerait d'implémenter les algorithmes qu'oncela impliquerait d implémenter les algorithmes qu on
veut comparer ;
◦ de plus, ces mesures ne seraient pas pertinentes car le
même algorithme sera plus rapide sur une machine plus
puissante ;
L’étude de complexité consiste donc à utiliser
des unités de temps abstraites proportionnellesdes unités de temps abstraites proportionnelles
au nombre d'opérations effectuées ;
On pourra par la suite adapter ces quantités enOn pourra par la suite adapter ces quantités en
fonction de la machine sur laquelle l'algorithme
s'exécute ;
8
s exécute ;

 La complexité temporelle d'un algorithme
consiste à calculer le nombre d'opérationsconsiste à calculer le nombre d opérations
élémentaires (affectations, comparaisons,
opérations arithmétiques,…) effectuées par unp q , ) p
algorithme.
 Ce nombre s'exprime en fonction de la taille n
des données.
 On s'intéresse:
◦ La complexité au pire: temps d'exécution maximum,
dans le cas le plus défavorable.
◦ La complexité au mieux: temps d'exécution minimumLa complexité au mieux: temps d exécution minimum,
dans le cas le plus favorable.
◦ La complexité moyenne: temps d'exécution dans un cas
édi d t d' é timédian, ou moyenne des temps d'exécution.
 Le plus souvent, on calcule la complexité au pire,
car on veut borner le temps d'exécutioncar on veut borner le temps d exécution
9

 Calculer le coût d’un programme revient à calculer le Calculer le coût d un programme revient à calculer le
nombre d’opérations effectuées en fonction de la taille
des données
 Pour déterminer le coût d’un algorithme, on se fonde en
général sur le modèle de complexité suivant :
ff l’é l d’◦ Une affectation, une comparaison ou l’évaluation d’une
expression arithmétique (+,-,/,*,//,%,**) ayant en
général un faible temps d’exécution considéré commegénéral un faible temps d exécution considéré comme
l’unité de mesure du coût d’un algorithme.
◦ Le coût des instructions p et q en séquence est laLe coût des instructions p et q en séquence est la
somme des coûts de l’instruction p et de l’instruction q.

◦ Le coût d’un test if◦ Le coût d un test if
if b:
p
else:
q
Le coût d’un test est égal au maximum des coûts des instructionsLe coût d’un test est égal au maximum des coûts des instructions
p et q, plus le temps d’évaluation de l’expression b.
◦ Le coût d’une boucle for
for i in range(n):
p
L û d’ b l f é l b d é é i iLe coût d’une boucle for est égal au nombre de répétitions
multiplié par le coût du bloc d’instructions p.
Quand le coût de p dépend de la valeur de i, le coût total de laQ p p ,
boucle est la somme des coûts de p pour chaque valeur de i.
11

◦ Le cas d’une boucle while◦ Le cas d une boucle while
while condition:
pp
Le cas d’une boucle while est plus complexe à traiterp p
puisque le nombre de répétitions n’est en général pas
connu a priori.
On peut majorer le coût de l’exécution de la boucle par
l b d é étiti ff t éle nombre de répétitions effectuées.
12

 Exemple: Exemple:
◦ Calculer la factorielle d’un entier n
1 affectation
(n-1) itérations
1 affectation + 1 multiplication
1 renvoi
Le coût de l’algorithme = Nombre total d’opérationsLe coût de l algorithme = Nombre total d opérations
1 Affectation + (n-1) *( 1 affectation + 1 multiplication)+1 renvoi
f( ) 1+ ( 1)*2+1 2*
f(n)=1+ (n-1)*2+1=2*n

 Exemple: Exemple:
◦ Vérifier la primalité d’un entier n
(n-2) itérations
1 reste + 1 comparaison1 reste + 1 comparaison
1 renvoi
1 renvoi
 
f1(n)=(n-2)*2+1
=2n-3
(n-1) itérations
1 reste + 1 comparaison
1 renvoi
1 renvoi
f2(n)=(n-1)*2+1n=2**31-1
f1( ) 4294967293
14
=2*n-1f1(n)= 4294967293
f2(n)= 92679

 Exemple: Calculer xn Exemple: Calculer x
1 affectation
n itérations
1 renvoi
f1(n)=1+n*2+1
2 2
1 affectation
(log2(n)) itérations
1 i
=2n+2
1 comparaison
1 reste + 1 comparaison
1 affectation + 1 division1 affectation + 1 division
1 renvoi
f2(n)=1+ (log2(n)+1) *(1+2+2+2)2
+ (log2(n)+1) *2+1
=9*log2(n)+11
La représentation binaire de n nécessite (log2(n)+1) bits
û l (l ( ) ) b 9 l ( )
15
Le coût maximal sur (log2(n)+1) bits = 9*log2(n)+11
X=3 et n=2**20-1
f1(n)= 2097152 et f2(n)=182

Calculer le coût des programmes suivantsp g
1 affectation
n itérations
1 affectation + 1 addition
1 renvoi
f1(n)=1+n*2+1
2 2=2n+2
1 affectation
n itérations
n itérations
+ 1 multiplication
1 renvoi
f2(n)=1+n*n*3+1
=3n2+2

Calculer le coût des programmes suivantsp g
1 affectation
n itérations
i itérationsi itérations
+ 1 multiplication
1 renvoi
f1(n)=1+(n*(n+1)/2)*3+1
=(3/2)n2+(3/2)n+2
1 affectation
log2(n)  itérations
1 condition
1 condition
1 renvoi
l ( ) 
f2(n)=1+log2(n) *3+1+1
=3*log2(n) +3

 Généralement, la complexité d'un algorithme
est une mesure de sa performance
asymptotique dans le pire cas ;
 Que signifie ‘asymptotique’ ?
◦ on s'intéresse à des données très grandes ;
 Que signifie ‘dans le pire cas’ ?
◦ on s'intéresse à la performance de l'algorithme dans
les situations où le problème prend le plus de temps.
 Pourquoi ?
ê û◦ pour être sûr que l'algorithme ne prendra jamais plus
de temps que ce qu'on a estimé. Ce qui correspond à
donner une majoration du nombre d’opérationsdonner une majoration du nombre d opérations
effectuées par l’algorithme.
18

 On dit que la complexité de l'algorithme est
O(g(n)) ou g est d'habitude une
combinaison de polynômes, logarithmes oup y g
exponentielles.
 Ce qui signifie que le nombre d'opérations Ce qui signifie que le nombre d opérations
effectuées, noté par f(n), est borné par
C*g(n) ou C est une constante lorsque nC g(n), ou C est une constante, lorsque n
tend vers l'infini.
19

Si f et g sont deux fonctions positives réelles:
f(n) = O(g(n)) si et seulement si le rapport f/g estf(n) = O(g(n)) si et seulement si le rapport f/g est
borné a l'infini (f est dominée par g):
◦ ∃C>0 ∃n >0 n>n f(n) ≤ C*g(n)◦ ∃C>0, ∃n0>0, n>n0, f(n) ≤ C g(n)
20

 La notation O dite notation de Landau vérifie La notation O, dite notation de Landau, vérifie
les propriétés suivantes :
 si f=O(g) et g=O(h) alors f=O(h)
i f O( ) t >0 l *f O( ) si f=O(g) et a>0, alors a*f=O(g)
 si f1=O(g1) et f2=O(g2) alors f1+f2 = O(g1+g2)
f ( ) f ( ) l f f ( ) si f1=O(g1) et f2=O(g2) alors f1*f2 = O(g1*g2)
17/12/2015
Dr. Atef MASMOUDI & Dr. Ameur
CH'HAYDER, IPEIS, AU:2015-2016 21

f(n) = (g(n)) ⇒ g est une borne inférieuref(n) = (g(n)) ⇒ g est une borne inférieure
asymptotique pour f:
◦ ∃C>0 ∃n >0 n>n C*g(n) ≤f(n)◦ ∃C>0, ∃n0>0, n>n0, C g(n) ≤f(n)
22

 f(n) = Θ(g(n)) ⇒f et g ont le même ordre de grandeur : f(n) = Θ(g(n)) ⇒f et g ont le même ordre de grandeur :
◦ ∃c1,c2>0, ∃n0>0, n>n0, c1*g(n) ≤ f(n) ≤c2*g(n)
23

 O(1) : complexité constante, pas d'augmentation du O(1) : complexité constante, pas d augmentation du
temps d'exécution quand le paramètre croit.
◦ Exemple: affectation, comparaison, …
 O(log(n)) : complexité logarithmique augmentation O(log(n)) : complexité logarithmique, augmentation
très faible du temps d'exécution quand le paramètre
croit.
◦ Exemple: conversion du décimal au binaireExemple: conversion du décimal au binaire
 O(n) : complexité linéaire, augmentation linéaire du
temps d'exécution quand le paramètre croit (si le
paramètre double le temps double)paramètre double, le temps double).
◦ Exemple: somme des n premiers entiers naturels
 O(n*log(n)) : complexité quasi-linéaire, augmentation
un peu supérieure a O(n)un peu supérieure a O(n).
 Exemple: calculer la somme des chiffres des n premiers entiers
naturels
17/12/2015

 O(n2) : complexité quadratique, quand le O(n ) : complexité quadratique, quand le
paramètre double, le temps d'exécution est
multiplie par 4.
◦ Exemple : algorithmes avec deux boucles imbriquées◦ Exemple : algorithmes avec deux boucles imbriquées.
 O(ni) : complexité polynomiale, quand le
paramètre double, le temps d'exécution est
lti li 2imultiplie par 2i.
◦ Exemple : algorithme utilisant i boucles imbriquées.
 O(an) : complexité exponentielle, quand le( ) p p , q
paramètre double, le temps d'exécution est élevé
à la puissance 2.
 O(n!) : complexité factorielle asymptotiquement O(n!) : complexité factorielle, asymptotiquement
équivalente à nn
17/12/2015

26

On suppose qu’on dispose d’un ordinateur capable deOn suppose qu on dispose d un ordinateur capable de
réaliser 109 opérations/seconde
17/12/2015

 Les instructions de base (affectation, comparaison,p
opération arithmétique,) prennent un temps constant,
noté O(1)
 On additionne les complexités d'opérations en séquence :
Instruction p O(f1(n))
I i O(f2( ))Instruction q O(f2(n))
O(f1(n)) + O(f2(n)) = O(f1(n) + f2(n)) =O(max(f1(n), f2(n)))
L b h t diti l Les branchements conditionnels :
17/12/2015
= O(max(f1(n) , f2(n), g(n)))

 La complexité d’une boucle for est égal au nombre d’itérations
multiplié par la complexité de l’instruction p si ce dernier ne
dépend pas de la valeur de i.
O(n*f(n))
 La complexité d’une boucle while:
= O(m*max(g(n) , f(n)))
17/12/2015

 Pour calculer la complexité d'un programme :p p g
1. on calcule la complexité de chaque partie du
programme;
2. on combine ces complexités conformément aux règles
' i d iqu'on vient de voir ;
3. on simplifie le résultat grâce aux règles de
simplifications suivantes:simplifications suivantes:
◦ On remplace les constantes multiplicatives par 1,
◦ On annule les constantes additives ;◦ On annule les constantes additives ;
◦ On conserve le terme dominant.
17/12/2015

Exemple: g(n)=5n3-6n2+4p g
◦ On remplace les constantes multiplicatives par 1,
1n3-1n2+4
◦ On annule les constantes additives ;
◦ 1n3-1n2
◦ On conserve le terme dominant.
◦ n3-n2
l ( ) ( 3)◦ Solution g(n)=O(n3)
17/12/2015

O(1)
n-1 itérations O(n)
O(1)
 La complexité de la fonction:
O(1)
 La complexité de la fonction:
17/12/2015

O(n)
O(n)O(n)
O(n)
17/12/2015

O(log(n))
O(log(n))
O(log(n))
17/12/2015

O(n2)
O(n2)O(n2)
O(n*log(n))
17/12/2015

 Montrez que la complexité de la fonction suivante estq p
quadratique en n, c’est-à-dire en O(n2)
1 affectation
n itérationsn itérations
1 affectation
k itérations
+1 division
1 renvoi
f(n)=1+n+2*(n*(n-1)/2)+3*n+1
=n2+3*n+2
17/12/2015
n +3 n+2

 Que fait cette fonction ? calcul de exp(1)
 Donnez une version linéaire de cet algorithme, c’est-à-
dire en O(n)
1 affectation
1 affectation1 affectation
n itérations
1 affectation +1 Multiplication
+ 1 addition
+1 division
1 renvoi
f(n)=2+6*n+1
=6*n+3
17/12/2015
6 n+3

 Complétez le tableau suivant.
Il s’agit de calculer le nombre d’opérations nécessaire
pour exécuter le programme en fonction de sa
Complexité n=10 n=100 n=1000
complexité et de la taille du problème traité
p
n
n2n
n3
2n2
n
log(n)
17/12/2015
log(n)

 Complétez le tableau suivant.
é éIl s’agit de calculer le temps nécessaire pour exécuter
un problème en supposant qu’on dispose d’un
ordinateur capable de réaliser 109 opérations/seconde
Complexité n=10 n=100 n=1000
ordinateur capable de réaliser 109 opérations/seconde
n
n2
n3
2n2
n
log(n)
17/12/2015
log(n)

 Rangez les fonctions suivantes par ordre de Rangez les fonctions suivantes par ordre de
grandeur croissant :
n n*log(n) n log(n) n log2(n) n2 (3/2)n◦ n, n*log(n),n, log(n), n log2(n),n2, (3/2)n,
n10, log2(n)
 Calculer la complexité des programmes:
 Premier et premier_rapide
 Puissance et puissance_rapide
17/12/2015

 Dire si les affirmations suivantes sont vrais Dire si les affirmations suivantes sont vrais
ou fausses:
◦ 2n+3=O(n)◦ 2n+3=O(n)
◦ 2n+log(n)=O(n2)
◦ 2n7+5n4+3n2+1=O(n7)( )
◦ 5n3+3nlog(n)+6n=O(n3)
◦ 3log(n)+2=O(log(n))
◦ 2n+100log(n)=O(log(n))
◦ 2n+2=O(2n)
17/12/2015

 Quelle est la complexité de la fonction Quelle est la complexité de la fonction
suivante:
O(n2log(n))
17/12/2015

cours de complexité algorithmique

Contenu connexe

Tendances

En vedette

Similaire à cours de complexité algorithmique

Dernier

cours de complexité algorithmique