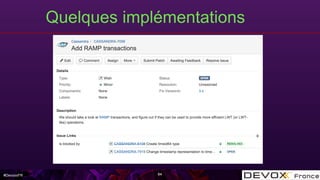
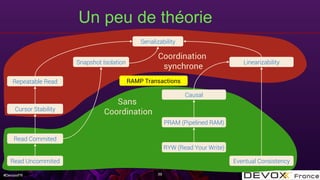
Le document aborde les algorithmes de données distribuées, en mettant particulièrement l'accent sur les CRDT (Conflict-free Replicated Data Types) et les transactions ramp, qui garantissent la cohérence des données dans des systèmes distribués. Il explique les défis de la convergence des données, les conditions nécessaires pour le fonctionnement des CRDT, ainsi que l'implémentation pratique dans des systèmes comme Apache Cassandra. La présentation couvre également des concepts théoriques liés à la sérialisation et à la visibilité atomique dans des transactions multi-partitions.























![#DevoxxFR
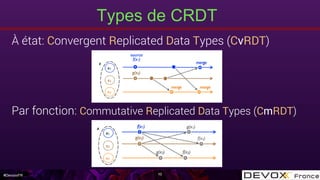
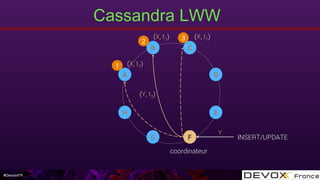
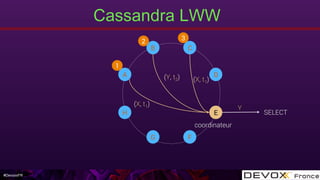
Cassandra LWW
Associativité
[("toto", t1), ("titi", t1)], ("tata",t1) à [("toto", t1), ("tata",t1)] à ("toto", t1)
("toto", t1), [("titi", t1), ("tata",t1)] à [("toto", t1), ("titi",t1)] à ("toto", t1)
Commutativité
("toto", t1), ("tata",t1) à ("toto", t1)
("tata", t1), ("toto",t1) à ("toto", t1)
Idempotence
("toto", t1), ("toto",t1) à ("toto", t1)](https://image.slidesharecdn.com/algorithmedistribuespourbigdatasaison2-devoxxfrance2016-160428133930/85/Algorithme-distribues-pour-big-data-saison-2-DevoxxFR-2016-29-320.jpg)










![#DevoxxFR
RAMP – Fast (Prepare)
45
Writer P1 P2
WRITE <X = 1,t1, {Y}>
Data=[ ], lastcommit=[ ]Data=[ ], lastcommit=[ ]WRITE X = 1
WRITE Y = 1
Prepare
Data=[<X = 1,t1, {Y}>]
WRITE <Y = 1,t1, {X}>
Prepare
Data=[<Y = 1,t1, {X}>]](https://image.slidesharecdn.com/algorithmedistribuespourbigdatasaison2-devoxxfrance2016-160428133930/85/Algorithme-distribues-pour-big-data-saison-2-DevoxxFR-2016-45-320.jpg)
![#DevoxxFR
RAMP – Fast (Prepare)
46
Writer P1 P2
Data=[<Y = 1,t1, {X}>],
lastcommit=[ ]
Data=[<X = 1,t1, {Y}>],
lastcommit=[ ]
Prepared
Prepared](https://image.slidesharecdn.com/algorithmedistribuespourbigdatasaison2-devoxxfrance2016-160428133930/85/Algorithme-distribues-pour-big-data-saison-2-DevoxxFR-2016-46-320.jpg)
![#DevoxxFR
RAMP – Fast (Commit)
47
Writer P1 P2
t1
Commit
lastcommit=[<X,t1>]
Commit
Data=[<Y = 1,t1, {X}>]Data=[<X = 1,t1, {Y}>]
t1 lastcommit=[<Y,t1>]](https://image.slidesharecdn.com/algorithmedistribuespourbigdatasaison2-devoxxfrance2016-160428133930/85/Algorithme-distribues-pour-big-data-saison-2-DevoxxFR-2016-47-320.jpg)
![#DevoxxFR
RAMP – Fast (Commit)
48
Writer P1 P2
Data=[<Y = 1,t1, {X}>],
lastcommit=[<Y,t1>]
Data=[<X = 1,t1, {Y}>],
lastcommit=[<X,t1>]
Committed
Committed](https://image.slidesharecdn.com/algorithmedistribuespourbigdatasaison2-devoxxfrance2016-160428133930/85/Algorithme-distribues-pour-big-data-saison-2-DevoxxFR-2016-48-320.jpg)
![#DevoxxFR
RAMP – Fast (Get)
49
Reader P1 P2
(X, ∅)
Get
lastcommit=[ <X,t1>]
Get
Data=[<Y = 1,t1, {X}>]Data=[<X = 1,t1, {Y}>]
(Y, ∅)
lastcommit=[ <Y,t1>]](https://image.slidesharecdn.com/algorithmedistribuespourbigdatasaison2-devoxxfrance2016-160428133930/85/Algorithme-distribues-pour-big-data-saison-2-DevoxxFR-2016-49-320.jpg)
![#DevoxxFR
RAMP – Fast (Get)
50
Reader P1 P2
<X = 1,t1, {Y}>
lastcommit=[ <X,t1>]
Data=[<Y = 1,t1, {X}>]Data=[<X = 1,t1, {Y}>]
<Y = 1,t1, {X}>
lastcommit=[ <Y,t1>]
Max(t1, t1) = t1
Xt1 = 1
Yt1 = 1 ✔︎](https://image.slidesharecdn.com/algorithmedistribuespourbigdatasaison2-devoxxfrance2016-160428133930/85/Algorithme-distribues-pour-big-data-saison-2-DevoxxFR-2016-50-320.jpg)
![#DevoxxFR
RAMP – Fast (Read & Write)
51
Writer1 P1 P2
WRITE <X = 1,t1, {Y}>
Data=[ ], lastcommit=[ ]Data=[ ], lastcommit=[ ]WRITE X = 1
WRITE Y = 1
Prepare
Data=[<X = 1,t1, {Y}>]
WRITE <Y = 1,t1, {X}>
Prepare
Data=[<Y = 1,t1, {X}>]](https://image.slidesharecdn.com/algorithmedistribuespourbigdatasaison2-devoxxfrance2016-160428133930/85/Algorithme-distribues-pour-big-data-saison-2-DevoxxFR-2016-51-320.jpg)
![#DevoxxFR
RAMP – Fast (Read & Write)
52
Writer1 P1 P2
Data=[<Y = 1,t1, {X}>],
lastcommit=[ ]
Data=[<X = 1,t1, {Y}>],
lastcommit=[ ]
Prepared
Prepared](https://image.slidesharecdn.com/algorithmedistribuespourbigdatasaison2-devoxxfrance2016-160428133930/85/Algorithme-distribues-pour-big-data-saison-2-DevoxxFR-2016-52-320.jpg)
![#DevoxxFR
RAMP – Fast (Read & Write)
53
Writer1 P1 P2
t1
Commit
lastcommit=[<X,t1>]
Data=[<Y = 1,t1, {X}>]Data=[<X = 1,t1, {Y}>]
lastcommit=[]
Reader1
(X, ∅)
Get
Get
(Y, ∅)
<X = 1,t1, {Y}>
<Y = ∅, 0>
lastCommit(X) = t1
lastCommit(Y) = 0](https://image.slidesharecdn.com/algorithmedistribuespourbigdatasaison2-devoxxfrance2016-160428133930/85/Algorithme-distribues-pour-big-data-saison-2-DevoxxFR-2016-53-320.jpg)
![#DevoxxFR
RAMP – Fast (Read & Write)
54
Writer1 P1 P2
lastcommit=[<X,t1>]
Data=[<Y = 1,t1, {X}>]Data=[<X = 1,t1, {Y}>]
lastcommit=[]
Reader1
Max(t1, 0) = t1
Xt1 = 1 ,Yt1 = ?
Get
<Y = 1,t1, {X}>
(Y, t1)
Lookup t1 from Data
Max(t1, 0) = t1
Xt1 = 1,Yt1 = 1 ✔︎
Commit
t1 lastcommit=[<Y,t1>]](https://image.slidesharecdn.com/algorithmedistribuespourbigdatasaison2-devoxxfrance2016-160428133930/85/Algorithme-distribues-pour-big-data-saison-2-DevoxxFR-2016-54-320.jpg)
![#DevoxxFR
RAMP – Fast (Read & Write)
55
Writer1 P1 P2
lastcommit=[<X,t1>]
Data=[<Y = 1,t1, {X}>]Data=[<X = 1,t1, {Y}>]
lastcommit=[]
Reader1
Max(t1, 0) = t1
Xt1 = 1 ,Yt1 = ?
Get
<Y = 1,t1, {X}>
(Y, t1)
Lookup t1 from Data
Max(t1, 0) = t1
Xt1 = 1,Yt1 = 1 ✔︎
Commit
t1 lastcommit=[<Y,t1>]
Si je vois une partition validée,
je peux voir toutes les
partitions liées, validées avec le
même timestamp ! (Tout)](https://image.slidesharecdn.com/algorithmedistribuespourbigdatasaison2-devoxxfrance2016-160428133930/85/Algorithme-distribues-pour-big-data-saison-2-DevoxxFR-2016-55-320.jpg)
![#DevoxxFR
RAMP – Fast (Read & Write)
56
Writer1 P1 P2
lastcommit=[]
Data=[<Y = 1,t1, {X}>]Data=[<X = 1,t1, {Y}>]
lastcommit=[]
Reader1
(X, ∅)
Get
Get
(Y, ∅)
<X = ∅, 0>
<Y = ∅, 0>
lastCommit(X) = O
lastCommit(Y) = 0](https://image.slidesharecdn.com/algorithmedistribuespourbigdatasaison2-devoxxfrance2016-160428133930/85/Algorithme-distribues-pour-big-data-saison-2-DevoxxFR-2016-56-320.jpg)
![#DevoxxFR
RAMP – Fast (Read & Write)
57
Writer1 P1 P2
lastcommit=[]
Data=[<Y = 1,t1, {X}>]Data=[<X = 1,t1, {Y}>]
lastcommit=[]
Reader1
(X, ∅)
Get
Get
(Y, ∅)
<X = ∅, 0>
<Y = ∅, 0>
lastCommit(X) = O
lastCommit(Y) = 0
Si aucune partition n’est encore
validée, toutes les partitions
liées retournent leur ancienne
valeur ! (Rien)](https://image.slidesharecdn.com/algorithmedistribuespourbigdatasaison2-devoxxfrance2016-160428133930/85/Algorithme-distribues-pour-big-data-saison-2-DevoxxFR-2016-57-320.jpg)

![#DevoxxFR
RAMP – Fast (Cas d’erreur)
59
Le client tombe après commit(X, t1)
☞ processus de maintenance pour valider les autres
partitions pas encore validées (force-commit)
Le client tombe après le dernier prepare
☞ processus de maintenance pour nettoyer Data[ ]
après un timeout](https://image.slidesharecdn.com/algorithmedistribuespourbigdatasaison2-devoxxfrance2016-160428133930/85/Algorithme-distribues-pour-big-data-saison-2-DevoxxFR-2016-59-320.jpg)
![#DevoxxFR
RAMP – Fast (Cas d’erreur)
60
Le client fait un rollback(ts) après le dernier prepare
☞ enlever les valeurs écrites à ts dans Data [ ]](https://image.slidesharecdn.com/algorithmedistribuespourbigdatasaison2-devoxxfrance2016-160428133930/85/Algorithme-distribues-pour-big-data-saison-2-DevoxxFR-2016-60-320.jpg)
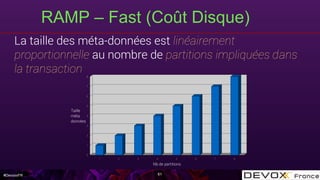

![#DevoxxFR
RAMP – Small (Prepare)
63
Writer P1 P2
WRITE <X = 1,t1>
Data=[ ], lastcommit=[ ]Data=[ ], lastcommit=[ ]WRITE X = 1
WRITE Y = 1
Prepare
Data=[<X = 1,t1]
WRITE <Y = 1,t1>
Prepare
Data=[<Y = 1,t1>]](https://image.slidesharecdn.com/algorithmedistribuespourbigdatasaison2-devoxxfrance2016-160428133930/85/Algorithme-distribues-pour-big-data-saison-2-DevoxxFR-2016-63-320.jpg)
![#DevoxxFR
RAMP – Small (Prepare)
64
Writer P1 P2
Data=[<Y = 1,t1>],
lastcommit=[ ]
Data=[<X = 1,t1>],
lastcommit=[ ]
Prepared
Prepared
🔍 🔍](https://image.slidesharecdn.com/algorithmedistribuespourbigdatasaison2-devoxxfrance2016-160428133930/85/Algorithme-distribues-pour-big-data-saison-2-DevoxxFR-2016-64-320.jpg)
![#DevoxxFR
RAMP – Small (Commit)
65
Writer P1 P2
t1
Commit
lastcommit=[<X,t1>]
Commit
Data=[<Y = 1,t1>]Data=[<X = 1,t1]
t1 lastcommit=[<Y,t1>]](https://image.slidesharecdn.com/algorithmedistribuespourbigdatasaison2-devoxxfrance2016-160428133930/85/Algorithme-distribues-pour-big-data-saison-2-DevoxxFR-2016-65-320.jpg)
![#DevoxxFR
RAMP – Small (Commit)
66
Writer P1 P2
Data=[<Y = 1,t1>],
lastcommit=[<Y,t1>]
Data=[<X = 1,t1>],
lastcommit=[<X,t1>]
Committed
Committed](https://image.slidesharecdn.com/algorithmedistribuespourbigdatasaison2-devoxxfrance2016-160428133930/85/Algorithme-distribues-pour-big-data-saison-2-DevoxxFR-2016-66-320.jpg)
![#DevoxxFR
RAMP – Small (Get round1)
67
Reader P1 P2
(X, ∅)
Get
Get
(Y, ∅)
lastcommit=[ <X,t1>]
Data=[<Y = 1,t1>,
<Y = 2,t2>]
Data=[<X = 1,t1>,
<X = 2, t2>]
lastcommit=[ <Y,t2>]
🔍 🔍](https://image.slidesharecdn.com/algorithmedistribuespourbigdatasaison2-devoxxfrance2016-160428133930/85/Algorithme-distribues-pour-big-data-saison-2-DevoxxFR-2016-67-320.jpg)
![#DevoxxFR
RAMP – Small (Get round1)
68
Reader P1 P2
t1
lastcommit=[ <X,t1>]
Data=[<Y = 1,t1>,
<Y = 2,t2>]
Data=[<X = 1,t1>,
<X = 2, t2>]
t2
lastcommit=[ <Y,t2>]](https://image.slidesharecdn.com/algorithmedistribuespourbigdatasaison2-devoxxfrance2016-160428133930/85/Algorithme-distribues-pour-big-data-saison-2-DevoxxFR-2016-68-320.jpg)
![#DevoxxFR
RAMP – Small (Get round2)
69
Reader P1 P2
(X, {t1,t2})
Get
Get
(Y, {t1,t2})
lastcommit=[ <X,t1>]
Data=[<Y = 1,t1>,
<Y = 2,t2>]
Data=[<X = 1,t1>,
<X = 2, t2>]
lastcommit=[ <Y,t2>]](https://image.slidesharecdn.com/algorithmedistribuespourbigdatasaison2-devoxxfrance2016-160428133930/85/Algorithme-distribues-pour-big-data-saison-2-DevoxxFR-2016-69-320.jpg)
![#DevoxxFR
RAMP – Small (Get round2)
70
Reader P1 P2
lastcommit=[ <X,t1>]
Data=[<Y = 1,t1>,
<Y = 2,t2>]
Data=[<X = 1,t1>,
<X = 2, t2>]
lastcommit=[ <Y,t2>]
tmatch= {t | t∈(t1, t2)∧X∈Data
return X | tX = max(tmatch)
tmatch= {t | t∈(t1, t2)∧Y∈Data
return Y | tY = max(tmatch)
X = 2
Y = 2](https://image.slidesharecdn.com/algorithmedistribuespourbigdatasaison2-devoxxfrance2016-160428133930/85/Algorithme-distribues-pour-big-data-saison-2-DevoxxFR-2016-70-320.jpg)


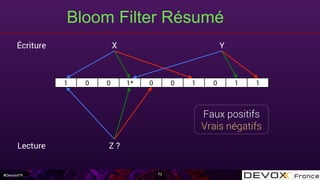
![#DevoxxFR
RAMP – Hybrid (Prepare)
74
Writer P1 P2
WRITE <X = 1,t1, BFY>
Data=[ ], lastcommit=[ ]Data=[ ], lastcommit=[ ]WRITE X = 1
WRITE Y = 1
Prepare
Data=[<X = 1,t1, BFY>]
WRITE <Y = 1,t1, BFX>
Prepare
Data=[<Y = 1,t1, BFX>]](https://image.slidesharecdn.com/algorithmedistribuespourbigdatasaison2-devoxxfrance2016-160428133930/85/Algorithme-distribues-pour-big-data-saison-2-DevoxxFR-2016-74-320.jpg)
![#DevoxxFR
RAMP – Hybrid (Get)
75
Reader P1 P2
(X, ∅)
Get
lastcommit=[ <X,t1>]
Get
Data=[<Y = 1,t1, BFX>]Data=[<X = 1,t1, BFY>]
(Y, ∅)
lastcommit=[ <Y,t1>]](https://image.slidesharecdn.com/algorithmedistribuespourbigdatasaison2-devoxxfrance2016-160428133930/85/Algorithme-distribues-pour-big-data-saison-2-DevoxxFR-2016-75-320.jpg)
![#DevoxxFR
RAMP – Hybrid (Get)
76
Reader P1 P2
<X = 1,t1, BFY>
lastcommit=[ <X,t1>]
Data=[<Y = 1,t1, BFX>]Data=[<X = 1,t1, BFY>]
<Y = 1,t1, BFX>
lastcommit=[ <Y,t1>]
Max(t1, t1) = t1
Xt1 = 1
Yt1 = 1 ✔︎](https://image.slidesharecdn.com/algorithmedistribuespourbigdatasaison2-devoxxfrance2016-160428133930/85/Algorithme-distribues-pour-big-data-saison-2-DevoxxFR-2016-76-320.jpg)
![#DevoxxFR
RAMP – Hybrid (Get)
77
Reader P1 P2
<X = 2,t2, BFY>
lastcommit=[ <X,t1>]
Data=[<Y = 1,t1, BFX>,
<Y = 2,t2, BFX>]
Data=[<X = 1,t1, BFY>,
<X = 2,t2, BFY>]
<Y = 1,t2, BFX>
lastcommit=[ <Y,t2>]
t2 > t1 ∧ X ∈ BFX ?
(X, t2)
Get](https://image.slidesharecdn.com/algorithmedistribuespourbigdatasaison2-devoxxfrance2016-160428133930/85/Algorithme-distribues-pour-big-data-saison-2-DevoxxFR-2016-77-320.jpg)
![#DevoxxFR
RAMP – Hybrid (Get)
78
Reader P1 P2
<X = 2,t2, BFY>
lastcommit=[ <X,t1>]
Data=[<Y = 1,t1, BFX>,
<Y = 2,t2, BFX>]
Data=[<X = 1,t1, BFY>,
<X = 2,t2, BFY>]
<Y = 1,t2, BFX>
lastcommit=[ <Y,t2>]
t2 > t1 ∧ X ∈ BFX ?
(X, t2)
Get Faux positif possible!!!](https://image.slidesharecdn.com/algorithmedistribuespourbigdatasaison2-devoxxfrance2016-160428133930/85/Algorithme-distribues-pour-big-data-saison-2-DevoxxFR-2016-78-320.jpg)