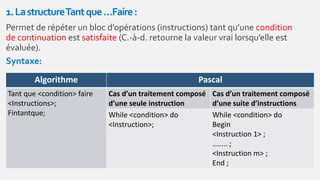
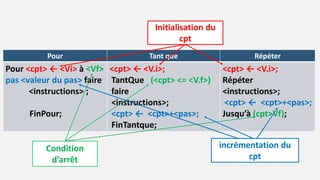
Ce document présente les structures de contrôle répétitives en programmation, se concentrant sur les boucles itératives complètes et à condition d'arrêt. Il explique les syntaxes de la boucle pour, tant que et répéter, et fournit des exemples pratiques, notamment pour le calcul de sommes et de factorielles. Enfin, le document propose plusieurs exercices d'application pour renforcer la compréhension des concepts présentés.

1. CHAPITRE:
Structuresdecontrôle
répétitives(Boucles) 1ere année LMD Sciences
et Technologies

2. Introduction
Itérative complète
Itérative à condition d’arrêt
Comparaison entre les trois boucles
Exercices d'applications
Sommaire:
1
2
3
4
5

3. INTRODUCTION

4. Les structures répétitives nous permettent de répéter un
traitement un nombre fini de fois. Elles permettent
d’exécuter plusieurs fois un bloc d’opérations
(instructions), tant qu’une condition (de continuation) est
satisfaite (retourne vrai).
On distingue deux types de boucles:
 Itérative complète (boucle POUR)
 Itérative à condition d’arrêt (Boucles TANT QUE et
RÉPÉTER)

5. ITÉRATIVE
COMPLÈTE

6. Une structure de contrôle itérative est dite complète si le nombre
de répétition est connu d’avance.
Elle est caractérisée par :
Un compteur (cpt) pour compter le nombre d’itérations est de
type entier;
L’initialisation automatique du compteur à une valeur initiale (Vi);
L’incrémentation de 1 (ou décrémentation de -1) du cpt
automatiquement à chaque répétition;
Vérification du cpt pour qu’il ne dépasse pas la valeur finale (Vf).
1.Structuredecontrôleitérative(BouclePour):

7. Syntaxe:
Algorithme
Pour <cpt> ← <Vi> à <Vf> pas <valeur> Faire
<Instructions>;
Finpour;
Pascal
Cas d’un traitement composé d’une
seule instruction
Cas d’un traitement composé
d’une suite d’instructions
For <cpt>:= <Vi> to <Vf> do
<Instruction>;
For <cpt>:= <Vi> to <Vf> do
Begin
<Instruction 1> ;
…….. ;
<Instruction m> ;
End ;

8. Remarque : Le <pas> est optionnel et permet de préciser la variation
du compteur entre chaque itération, le pas par défaut = 1 et
correspond donc à une incrémentation.
Si le pas = -1 la syntaxe en pascal devient : For <cpt>:= <Vi> downto
<Vf> do
Exemple : Calcul de la somme des 100 nombres entiers
La somme S des cents premiers nombre:
S=1+2+3+4+5+…+100.
Nous remarquons que à chaque fois on ajoute 1
(incrémentation par 1) au nombre précèdent puis on
l’ajoute à la somme S.

9. Solution
0
S
i
1
1
S
i
3
2
S i
6
3
S
i
10
4
S
i
12
5
S
i
0+1
1+2
3+3
6+4
10+5
…
…
S
i
….
5050
100
S
i
4950
+100
Algorithme Somme;
Variable
I,S: entier;
Début
S:=0;
Pour i← 1 à 100 faire
S ← S+i;
Finpour;
Ecrire(‘la somme =‘,S);
Fin.

10. ITÉRATIVEÀ
CONDITION
D’ARRÊT

11. Une structure itérative est dite à condition d’arrêt si le nombre de
répétition n’est pas connu d’avance, mais il dépend d’une condition.
On distingue deux types :
Boucle Tant que …… Faire
Boucle Répéter ……. Jusqu’à

12. Permet de répéter un bloc d’opérations (instructions) tant qu’une condition
de continuation est satisfaite (C.-à-d. retourne la valeur vrai lorsqu’elle est
évaluée).
Syntaxe:
1.LastructureTantque…Faire:
Algorithme Pascal
Tant que <condition> faire
<Instructions>;
Fintantque;
Cas d’un traitement composé
d’une seule instruction
Cas d’un traitement composé
d’une suite d’instructions
While <condition> do
<Instruction>;
While <condition> do
Begin
<Instruction 1> ;
…….. ;
<Instruction m> ;
End ;

13. Fonctionnement de la boucle:
La condition de continuation est évaluée.
Si sa valeur est faux, le bloc d’opérations n’est pas exécuté,
et l’exécution d’algorithme/programme se poursuit à la
suite de fintantque.
Si sa valeur est vrai, le bloc d’opérations est exécuté. À la fin
de l’exécution du bloc, on « remonte » pour évaluer à
nouveau la condition de continuation, selon les règles
précédentes.

14. Cette structure permet de répéter un bloc d’opérations jusqu’à ce
qu’une condition d’arrêt soit satisfaite.
Syntaxe:
2.LastructureRépéter….Jusqu'à:
Algorithme Pascal
Répéter
<Instructions>;
Jusqu’à <Condition
d’arrêt>;
Repeat
<Instructions>;
Until <Condition
d’arrêt> ;

15. Fonctionnementdelaboucle:
Le bloc d’instructions est exécuté. La condition de terminaison
est évaluée a chaque exécution:
Si sa valeur est faux → le bloc d’opérations est exécuté à
nouveau.
Si sa valeur est vrai → la répétition s’arrête et l’exécution se
poursuit à la suite du jusqu’à ( la fin de boucle).

16. COMPARAISON
ENTRE LESTROIS
BOUCLES

17. Quelle boucle choisir ?
Si on connait le nombre d’itération à effectuer dans la boucle, on
utilisera une boucle pour .
Si la poursuite dans la boucle est dépendante d’une condition, on
utilisera de préférence l’une des deux boucles: Tant que ou répéter.
Lien entre Pour etTant que/ Répéter:
La boucle Pour est un cas particulier de Tant Que/Répéter (cas où le
nombre d'itérations est connu et fixé) . Tout ce qu'on peut écrire avec
Pour peut être remplacé avec TantQue ou bien répéter (la réciproque
est fausse)

18. Pour Tant que Répéter
Pour <cpt> ← <Vi> à <Vf>
pas <valeur du pas> faire
<instructions> ;
FinPour;
<cpt> ← <V.i>;
TantQue (<cpt> <= <V.f>)
faire
<instructions>;
<cpt> ← <cpt>+<pas>;
FinTantque;
<cpt> ← <V.i>;
Répéter
<instructions>;
<cpt> ← <cpt>+<pas>;
Jusqu’à (cpt>Vf);
Condition
d’arrêt
Initialisation du
cpt
incrémentation du
cpt

19. Traitement
n fact
Supposons que n=5, nous avons fact= 5*4*3*2*1
= 1*2*3*4*5
Nous remarquons que le nombre s'augmente
constamment par 1.
1
fact
i
1*2 2
fact
i
1*2*3 3
fact
i
1*2*3*4 4
fact
i
1*2*3*4*5 5
fact i
Arrêt (n=i) fact= 120
Exercice:donnerl’algorithmequicalcullefactorield’unnombren(utilisant
les3boucles:pour,tantqueetrépéter).

20. La boucle Pour La boucle tant que La boucle Répéter
Algorithme Factoriel;
Variable
fact, n, i : entier;
Début
Ecrire (‘ donner la valeur de
n’);
Lire (n);
fact1;
pour i1 a n faire
factfact*i;
Fpour;
Ecrire (‘Le factoriel est égale a
‘,fact);
Fin.
Algorithme Factoriel;
Variable
fact, n, i : entier;
Début
Ecrire (‘ donner la valeur de
n’);
Lire (n);
fact1;
i1;
Tant que (i<= n) faire
factfact*i;
ii+1;
Ftq;
Ecrire (‘Le factoriel est égale a
‘,fact);
Fin.
Algorithme Factoriel;
Variable
fact, n, i : entier;
Début
Ecrire (‘ donner la valeur de
n’);
Lire (n);
fact1;
i1;
Répéter
factfact*i;
ii+1;
Jusqu’à (i>n);
Ecrire (‘Le factoriel est égale a
‘,fact);
Fin.

21. EXERCICES
D'APPLICATIONS

22. Exercice N°1 :
Ecrire un algorithme puis un programme qui demande
un nombre de départ, et qui calcule la somme des
entiers jusqu’à ce nombre. Par exemple, si l’on entre
5, le programme doit calculer : 1 + 2 + 3 + 4 + 5 = 15
NB : on souhaite afficher uniquement le résultat, pas
la décomposition du calcul.

23. Exercice N°2 :
Ecrire un programme en Pascal qui calcule et
affiche la somme suivante :
S=-1+1/2-1/3+1/4-1/5+⋯+1/n

24. Exercice N°3 :
Ecrire un programme en Pascal qui lit une suite de
nombres se terminant par 0 et calcule et affiche le
nombre des nombres positifs et le nombre des
nombres négatifs.

25. Exercice N°4 :
Un nombre est parfait s’il est égal à la somme de ses
diviseurs stricts (différents de lui-même). Ainsi par exemple,
l’entier 6 est parfait car 6 = 1 + 2 + 3. Écrire un programme
permettant de déterminer si un entier naturel est un nombre
parfait.
Tester le programme avec les nombres : 6, 28, 496, 8128