Le document contient des références à divers concepts mathématiques et algorithmiques, ainsi qu'à des méthodes de modélisation et d'analyse. Il présente des sections sur les propriétés des fonctions, les structures de données et d'autres notions techniques. La structure du document est multiple et inclut des exemples et des définitions précises.

1. ! " #$%& #$ &'
681.3.14/21:519.713
( ) *
+ , + ) *
05.13.05 - '
:
) -. # ! & &',
- ,
– 2016

2. 2
!"#$%
$ &'& ( ), *& +',- )%# . ,$('%/0#1 6
.$% + 8
'&! #2 1
&32) 4 /"( %/25 ,6 4&'" +'( $%/.2( ) %/
$+&$&7#. "# #"#!/0#1 7 2(.,6 4 0#-
15
1.1 &
’
15
1.1.1 + ’
15
1.1.2 % 8 8 17
1.2 & , , 9
. 7 8. ,
,
18
1.3 4 21
1.3.1
21
1.3.2 / 23
1.3.3 - 8
24
1.3.4 27
1.3.5 Cognate- :
29
1.4 7
31
1.4.1 + ; 8 31
1.4.2 4 31
1.4.3 + 34
1.5 " 8 35
1.5.1 " 35
1.5.2 " –" - 35
1.5.3 " 7 –+ 36
1.5.4 " 36
1.5.5 " + 36
1.5.6 " -. 37
1.5.7 " ’ 38
1.5.8 " #- ( /7&- ( 39
1.6 8 8 40
1.7 + : 42
. 1 44
'&! #2 2
& ; 46
2.1 8 : f(n) 46

3. 3
2.1.1 & < 8 :
f(n)
46
2.1.2 3 8
: L(n) 8 48
2.1.2.1 + 48
2.1.2.2 . = 8 ,
9
50
2.1.3 > 52
2.1.3.1 & 8
8 >
52
2.1.3.2 3 55
2.1.4 ' ; 56
2.1.4.1 $ ; 56
2.1.4.2 + ; 59
2.1.5 " - 63
2.1.6 7 8 : L(n) f(n) 63
2.2 & ;
64
2.2.1 &
64
2.2.2 7 8 8 65
2.2.3 7 = –
8 72
2.2.4 . 8 8
76
2.2.5 " BF &'4+ =
78
. 2 79
'&! #2 3
"(%& , "# #"#!/0#1 7 2(.,6 4 0#-
. &'%&3& /25 #- 4&'"# +'( $%/.2( )
81
3.1 & < 8
81
3.2 "
; 82
3.3 " 8
8 ; ; =
87
3.4 "
8 8 ; ; =
100
3.5 " 8
8 ; ; =
107
3.6 " 116

4. 4
8 8 ; ; =
3.7 " 8
8 ; ; =
119
3.8 " 8
8 ; ; =
122
3.9 "
8 8
124
3.10 " BF &'4+ =
138
. 3 140
'&! #2 4
/+/'/% &-+'&3'/" ,- &"+2( $ "# #"#!/0#1 7 2(.,6
4 0#- %/ '(/2#!/0#) / -&3& &$ &.# ,$ '(% ,6
+',$%'&1.
143
4.1 $ = , 9 8 , 9
143
4.1.1 ' : , 9
8 8
143
4.1.2 ' 8 , 9
, 147
4.2 $ -
8 , 9
149
4.2.1 + - 149
4.2.2 4 : 8
150
4.2.2.1
150
4.2.2.2 %
153
4.2.3 . &"+2( $ 8
8 157
4.2.4 . &"+2( $ 8
8 160
4.2.5 . &"+2( $ 8
8 162
4.2.6 . &"+2( $ 8
8 165
4.3 7 ;
8
167
4.3.1 ! ; 167

5. 5
8
4.3.2 7 171
4.3.3 7 ; in
if / ; out
if 173
4.4 7 ;
8
181
. 4 183
.,$ &. , 185
$+,$& ., &',$%/ ,6 ?('(2 188
& /% ,

6. 6
*, / ) * ,
DP -
BF -
CHO BF -
ChO SBF -
$
Cognate- + - 8
Cognate-+) -
KPF - -
PO BF - +
PO SBF -
+) -
,) - / -
+ -
-
+ - '
+ - '
+ - '
-
+) -
+ -
- -
+ - '
0 ) - ;
0 + - ;
+) -
- ;
+) - ' -"
+ - '
BF - 8 8

7. 7
+ - 8
+) -
+) + - BF
, -

8. 8
1
)
1 $#.- . &. + ; , 9
; 8 8
, ; = = ; .
=, 9 , ,
8 (DP), = 8 : .
9 :
8 , 9 8, ; =
:
1) DP;
2) ; DP;
3) ; 8 ,
8.
; =
– DP ; ; 8
(BF), .
+ 8 8
, =
. 4 = .(. > [39-42],
#.$. ' [35, 36], .$. " [38, 96], #.#. ? [48-50], (.. , ". ,
.. [101-104], (. " - [105], 3." , (." , ..".3 ; [51-54],
./.+ [55-62], /. .! [64-77], ;
’ 0 [43-45], ... / [46],
[47].
1
–
!
" . #
.

9. 9
& 8 8 BF
; 8 BF. $ CS
= 8 8 BF, 8
.(. > , 3. . + , /. /; , , /. . ! ,
'.". , '.". ' , #.$. ' . !
$...) [79], ..+.$ , ..+.% , +.".7
[80, 81], /. .! , .. ." , ..$.. , /./.> [82-88],
..".$ [89, 90], '.$.$ , @.&. [109-150].
; ; = - & 2 - 3 0$%$' 3 CS
( ) – CS, 9
.
" : : 9 : = .
( ’40 1 5 & 0 -$ 1 & & 6 ! $ $ &, 6#$-$ &, $ &.
: : .
. ; - "
8 , 8 8 8 20.12.2013 A179
„& : ; :
, 8 8
8 2014–2018 ”, . 1.2.9.1. “' 8
8 8 ”, -
8 “. ;
” ( :
= 8 0109U001880), .
$ $ 0$%$' % # %7 -. = ; : 8 - 8
9 8
8
(&'4+).
8 ; -$ 6- 0$%$' :
1. 8 : 8 :
; 8 8 8 &'4+.

10. 10
2. ' 8
&'4+.
3. + 8
8.
$ ' = 8 .
% = 8
&'4+.
& . : 8 :
= 8 : . $
8 , 8
8
8 . +
8 &'4+
8, . '
8
= 8 8
.
$ 1 $ - &0-$ & $-&8 0 #. $ .
1. . ; 8 8
; = ’ :
8 8 8 8 8
: 8 : , 8
, 9 8
8 ; 9
: , 9
8 , 9
< 8 .
2. . ; 8
8 8 ;

11. 11
8 8, 9 ;
8 .
8 - 8
-
.
3. & ; 8
8 ;
8 , 9 9
8 , ,
,
8.
) $1 &'- 0-$' --4 & $-&8 0 #. $ . +
=
: , , 8 ,
8 &'4+
’ .
: : :
- &'4+, =
= ’ :
= 8 8
. = : : =
8 SL, SAD, 9 = SS:
1) 10%
;
2) 32%
;
3) 2
, 9 : A1;
- : 8 :
, 9 = : ; :

12. 12
: ’= 8 :
. : 8 :
= : : 8, :
. & :
; , : =8 :
= ; ;
- 8 &'4+ –
8 8, 9 = : 4,7
8
8 8 ; ;
; = ;
- 8
, = :
8 , 9 -
- . +
8, 9
= 8;
- 8
8 , 8 :
8 : , 8.
+ : :
: = "
8 .
$# 0$9 4. '
: . & :
: : : =
«&',!& - /.I3/0I)» ( : « '&7&'& +'&"», . "
24, . $ i , ., 8 , 20708)
GALILEO BEIDOU ( : A 006.06.612
07.05.2014 .); :

13. 13
: (/ :
15.09.2015 .), 8 (/
: A 031/48/713 14.10.2015 .), : -
: (/ : 16.06.2014 .)
5& &" - 1 0% 5 $'$. & :
: . [11] [13] = ,
[8] [12] . . ,
, : : : 8 :
8 : [1, 2, 3,4]; : 9
8 8 8
[5]; : 8 [1-5];
8 [6 ,7, 8, 12,
13, 17, 18]; 8
[10, 11]; COGNATE- 8 [9];
8
8 [14, 15, 16].
6 5$9 4 0 #. $ %& $9 :. & : 8
14 : : 8 :
: - 8 «# 8 ,
» ( , 2012); V# : -
8 «$ ,
» (! :: , 2012); II : -
8 «4 - 8 ,
, - » ( , 2012); #, ## ###
8 - Internet- 8 «/
’ - 8 : , ,
: 8 8 - 8 Internet-
8» ( , , 2013, 2014, 2015); : -
8 «B » 17- " : :
«' C : 66# » (6 , 6 '(, 2013); IV

14. 14
: - 8 «&
» ( , % , 2013); I : - 8
«+ D » ( D- -% -+ , 2013);
8 - 8 «## :: ,,
» ( , % , 2015); -
8 «# , , . #"/_2015» ($ , $ , 2015);
8 - 8 , ,
«+ : .
» (" , + % , 2015); 6VIII . -
8 : , 120-
«$ D D C » ( , $4 ,
2015).
) 5# 1$9 :. & : 32
, 18 – . & 2
, 2 : 2 8, : 14
.
1 $ $ 5 4! %& $9 :. = = ,
, , : (150 )
. 69 , 31 , 1 . +
8 = 209 , 167 .

15. 15
( 1
* + + ) *
) ( , + ,
1.1 !#4% -% -9 " 0 & 1 $ -$6 4 1 &- 0 8- '-&8 1 6 - -
1 6’3 -&8 & -$ - 5 # &8 ; -19 "
1.1.1 ) 6 1 & & &- 0 1 6’3 -&8 & -$ - 5 # &8
; -19 "
+ 30- ,
8 8 [100-105],
: ;
; = . &
8 8
8 8 .
" : :
, 9
:
9 : . +
;
; , 9 ; , = ;
; ’ ,
9 8 , 9 ;
; .
' ; : 8 8 8
8 ,
’
, : ’= , ,
, 8

16. 16
: ’= ’= ,
; , 9
’ .
=
8 8 8 , , ’
.
= ; = ;
8 ; ; 88 . -
, : 8
; 9 9 9 9
8 : =8 8 : , ,
; 8 = ;
8 8
8 8 . %
, ’ = 8
; ;
; 8 : 9
, :
: 8
« » , .
$ 8 8
= ,
8 8 8 .
& : .
+ , 9
; 8 8. . 8 : :
8 8
9 8. +
: , 9

17. 17
(24)
= BF.
1.1.2 -% -9 : 0 & 1 5'& #3 $#.- : 8- 1&
! ; ' = =
; : 8 8 . . :
: : = , 9 :
; ; , : . %
9 8 : #%-
9 = 15 . . & –
8 8 « - ; » 8.
0 8
, , .
; ;
= ,
8 .
= :
• : ;
, 9 = , ;
, ; ; ;
• ; 8 ,
: ,
, ;
• 8 -
; =
;
• 8 8
; ;

18. 18
• ; , '
8 ; .
$ ; 8
-
; = 8
. % , : :
; , ; BF,
07, 9 ;
'
1.2 - - -&, 0-$' --4 $ &0-$' --4, < &1 & 3 . 4
%& $9 "- " 5 . # ; #& 5 # ; -19 :. #$ &; 1$9 4,
$5 #3 $--4, #$ &
! ,
: ,
, = : .
7 8 . :
: 1,..., n BF f(x1, ..., n), , :
, 9 0 1 [80-81].
; BF =
(%# BF), , 2n
1, ..., n : =
8. , . 1.1 = BF f( 4, 3,x2,x1), = 1
1000, 1100, 0001, 1001 . ., 0 0000, 0010, 0100, &11&
. . [107]
" : , BF f( 4, 3,x2,x1) = 0, =
&f
0
, : , BF f( 4, 3,x2,x1) = 1,
= &f
1
. & , 9 '= : &f
1
, &f
0
= : V

19. 19
2n
: 1,..., n, =
n, n- .
74, 8 V ,
= (PO BF). ) 9 :
BF ( , : ),
BF = , (ChO BF). ChO
BF = : &f
1
, &f
0
88 .
CHO BF f1(x1, ..., n) f2(x1, ..., n) , 9 9 &f1
0
=&f2
0
,
&f1
1
=&f2
1
. CHO BF f1(x1, ..., n) = CHO BF f2(x1, ..., n)
( = f1(x1, ..., n)E f2(x1, ..., n), 9 9 00
21 ff MM ⊆ 11
21 ff MM ⊆ . .
, 9 f2(x1, ..., n) = f1(x1, ..., n).
' 1.1
($%$--4 BF 0$ % 6 ! 3 $5#&9. &--
x4 X3 x2 x1 y
0 0 0 0 0 0
1 0 0 0 1 1
2 0 0 1 0 0
3 0 0 1 1 1
4 0 1 0 0 0
5 0 1 0 1 0
6 0 1 1 0 0
7 0 1 1 1 0
8 1 0 0 0 1
9 1 0 0 1 0
10 1 0 1 0 0
11 1 0 1 1 0
12 1 1 0 0 1
13 1 1 0 1 0
14 1 1 1 0 1
15 1 1 1 1 1
7 ; BF : , 9 ; ,
= 1 ( 0). " : , BF f( 4, 3,x2,x1)
= 1, = : = &f
1
, ( , BF, %#
. 1.1), :

20. 20
)15,14,12,8,3,1(),,,(
1
1234 ∨== xxxxfy
* ; : CHO BF
– %# (0, 1, *) [107]. ,
%#, - ( ) = 0
1. , BF, %# . 1.1, =
1101000100001010. BF. ; 8 :
BF ; 10 +$ (11010001000010102=5351410)
16 +$ (11010001000010102=D10A16).
) : , : , 9 =
, = 1 .
. ! : 0 2n
, n –
.
, %#, =
0, 1 «*». + «*» %#, .
%
, ; 0 1
«*» . ) 9 n- = l
«*», : = 2l
, 9
V [75-76].
% , : ,
.
7 - BF : ' 8 8
( 4), ' 8 ' .
6 : : '=
, ' , 9 '
4. ) 9 4 : ' = ,
, 4 = ( 4).
+ BF , 9 ; = ,
PO BF f(n), 2n
. & BF =
n

21. 21
1.3 + & 6 % $ # --4 5 # &8 ; -19 "
1.3.1 #$ &'-$ ; $ 6 % $ # --4 41 % -$- -$ ; $
6 % $ # --4 5 # &8 ; -19 "
;
BF : ( 4+) –
’ 8, ’ 8 ( #-/7&- ().
+ 4+ = 8
, :
: ,
; , 8 8 ,
. 4+
8. & , ’ = 4+, 9
XIX . ; 8 , ; ,
8 40-50 XX ’
8 -
; [100-105]. . 50-80
8,
8
. ! , 1953 1986 : «" »
« » 800 , 8.
. 8, , . ;
BF, , %# = ’
( 4) 4. ;
; 4 4,
; – 4 (" 4). ! ;
BF = : , , ,
; 8.

22. 22
; 8
: (4/2)
8 9 . $ :
7 -+ , , + .
= 8 ’ 8
. & = , 9
, : . !
= : , = , : : , 9
= , 8 8, 9 , =
; : : , 9 = 8.
4 , : = : . % , ,
9 8 :
• = 8;
• : " 4;
• : : 4
" ( ) [101-104] 8 (
) = 8 4
8 4. " - [26] , ,
9 = .
-" - ; = ; 8
4+ " 4.
[105]. & , 9 : =
8 BF BF, = , 9
8 , : .
" 8 -. ,
= : BF
.
.
8 [97-99]. % 9
4 @.#.? [106].

23. 23
8 4+ = :
, : ; = .
. : ; ; BF
8 BF.
! 8 4,
; 4
4. / 4+
. + ;
8 = ’= . 0 , 9
: = :
. ! 8
. & =
« » ;
: .
1.3.2 #. -$ & - ; & 6 % $ # --4 5 # &8 ; -19 "
$ , 9 4+ 8
07 = = : ; . . ;
. . ;
1928 #.#.? [48-50] ; ? .
: , , ’ ;
8 BF : 8
: 8 . # :
BF 9 50- ’ 8 . .
." #.' [35, 36, 38] ?
8 , 9
« ' -" ». $ , 9 ?
- 8 BF = 2 ’ ,
. , 8

24. 24
BF, ' -"
. ' , 9 9
BF =
.
? ' -"
BF [35]. # BF
' -"
8. . 2n
BF
' -" , 9 : = ; 8 –
9 BF : . 0 ;
[37-38].
+ BF
? ' -" =
, 9 = = . +
= ;
#, /7&, #.
1.3.3 1 -6 "-$ ; -19 4 41 #39 "-&" 0 & 1 $ &; &'- :
; & 6 % $ # --4 5 # &8 ; -19 "
" : 8 8 BF
; [109]. + ; [134]
BF ;
: . . [137]
. - . +
: BF - ( . : ), [10]
8 .
! , p BF n- :

25. 25
);,...,(
.....................................
);,...,(
);,...,(
110
)1()1(
110
)1()1(
110
)0()0(
−
−−
−
−
=
=
=
n
pp
n
n
xxxfZ
xxxfZ
xxxfZ
(12)
9 %#, : n
= - .
' ),......,,( 110
)()(
−= n
ss
xxxfZ , 9 :
%#, : . %#
Z : . % : %# :
8 8, 8 0, 1, 2,…, 2n
-1,
:
−
=
=
1
0
2
n
S
S
Sxx ,
(13)
−
=
−−
=
1
0
1)(
2
p
S
SpS
ZZ .
(14)
. (13) = %#, Z (14) –
[ ])1()1()0(
,....,, −p
ZZZ %#, 8
.
! : - 8 8
( +4) (( ) :
)[ 1,)()( +∈=Φ δδδ xZx (15)
& [0, n
), : L2
:
4 '=,
,)()(
0
xfCx kk
k
∞
=
=Φ )
kC – = ;

26. 26
)(xkf – 8 8 8 { x)f(k, }.
. [6] : -
( +4),
8 .
BF, : 8 , 4-
. . (- : BF
- (KPF), 2n
,
= 0 1 : [1] = (16)
f(x1,x2,x3,…,xn) − BF, 9 = 8 ( );
− q- 8 [16], 9 : (- ;
− = q- , 9
, - BF = , - ;
.
. 1.1 {q(i,n)} BF
3 (n=3).
03q
13q
23q
33q
43q
53q
63q
73q
' . 1.1 - $ q- n=3

27. 27
1.3.4 6# 1 - ; & 6 % $ # --4 5 # &8 ; -19 "
. [108-109] = : =8 BF
– , 8 ' -"
9
: . . [99] 8
8 8 BF. : 8 :
n :
8 : : , 9
: – «
: », 8 8 – « : : » [46,52].
9 8 8 88
; 8 8. . [45-52]
: : 2, 3 4
8 , 8 ' -"
. 0 : 8
8 8 8 : n .
$ ’
: ; ,
’= 8 : ; 8.
: : 8
8 [110]. .
8 (.+ , 7.' ,
/.% , $.) , .7 , . , 3.' , ..> ,
.. . ! = 9
, 8. . [111]
= , 9 8
, , : = 9
8 , .
! , =

28. 28
; ; ’= , 9 ; 8
; 9 9 .
& :
, 8 , 9
; =8 . .
8 8
? , ' -" , ,
.
:
8 . !
.
$ 8 9 8
. 8 8 8 :
: 8 8
8
. " -
8 8
8. $ , 9
,
8 , ; =
8 . 0 = 8
: , 9 8 .
.
’ ; ’ 9 ;
. ’ :
, 9
8 , 8, ,
, ’ , 9
= ,
: 9 ; ;

29. 29
. 0 ; 8
@.&. [26] : 8
8 8 , 8
9 = : - 8 8 8 . $
8
: , =
8, : ;
.
1.3.5 Cognate-; $ 6 % $ # --4 41 ; $ 6 % $ # --4 - 7&-
5#&0.1&8 5 # &8 ; -19 "
(0/) =,
, ; 8 . # ;
: , 0/ ,
, %# 0/ =
, : , ; = 8
.
% = = , ’ 8
:
1. + " ( ; ) +% ( )
2. + /0+ ( -
)
3. &
8 0/ = :
; « » – 8 8. )
, $ = , ,
; .

30. 30
0/ = 8
, , 9 m BF, 8
: 8 :
∨∨∨=
∨∨∨=
],[][][
];[][][
)()(
1
)(
)(
1
)(
11
)(
11 1
n
mp
n
m
n
mm
n
p
nn
XFXFXfZ
XFXFXfZ
m
(9)
X(n)
– n, $;
f1[X(n)
], f2[X(n)
], …, fm[X(n)
] – BF, 9 $ %# ; ,
BF, : $;
F11[X(n)
], F12[X(n)
], …, F1p1[X(n)
] – 8 8 f1[X(n)
];
Fm1[X(n)
], Fm2[X(n)
], …, Fmp1[X(n)
] – 8 8 fm[X(n)
].
9 : X(n)
(9)
: , (9) :
∨∨∨=
∨∨∨=
.
;
1
11111 1
mmpmmm
p
FFfZ
FFfZ
(10)
# (10) , 9 : BF m %#
; , : )i
« » . 8 =
(10) , Fi (10) )i=1. ' $,
BF Zi : 8
, = Cognate- $# 0$9 =3 ( . « ognate» – ,
: ), , Fi
= , Cognate- +, )i 4+ Cognate-74
= Cognate-+) ($_4+).
7 - BF ikF (10) « » 8 if ,
, : 8 8 ,
(10) = . «7 » : ikF if :
, : $ 0/ .
: BF (10) : :

31. 31
)()(),,,(
12
0
21 knijkij
i
ni xxQxxxZ
n
−
−
=
Φ= , (11)
ijQ – 8 [42], 9 = (11)
: kx ( nk <≤0 );
)( knij x −Φ – 8, 9
BF ;
U – (11), :
’ 8 ( 4+), 8 ( /4+)
mod2 ( ? , '"4+, [42]).
1.4 $0& 5 # &8 ; -19 " 41 - $ ; & 6 % $ # --4 5 # &8 ; -19 "
1.4.1 ) % $ # --4 5 # &8 ; -19 " ' 0 -2 5 # ; -19 :
& = = 8 8 BF =
- 8 BF : 8 (74) ;
BF. - 8 BF n :
BF.
+ ( ) 8 : L(n) BF n
= BF, :
BF - BF 8 : .
' = BF,
BF = .
1.4.2 + -19 -$#.- 6 - & & 5 # &8 ; -19 "
7 - BF : ; BF. #
BF, : -
BF. +

32. 32
BF. & = :
, : .
& = = BF = - 8
BF : 8 (74) ; BF.
- 8 BF n :
BF.
+ ( ) 8 : L(n) BF n
= BF, :
BF - BF 8 : .
( * * BF ((%#+()
BF {f1, f2,..., fk}, * BF f
" .
+ 8 =
. ' ' =8
8 8 [9].
BF, = 8, = :
, - = , 9 : :
: . $
, . + : , 9
' , 4+$74 , 9 88
8 : ' .
+ BF =:
1. 74, 9 0;
2. 74, 9 1;
3. $ 8 BF;
4. 2 BF;
5. " BF.
, , S BF *,
, " BF,

33. 33
1, " BF, 0, " BF, "
BF " BF
4+$74 :
BF BF =8 8 ( . . 1.2)
' 1.2
) # 1 BF, < 4 . 1 $ ! -
! - 0 #. $
f0 F1 f2 f3
x
0 1 2 3
0 0 1 0 1
1 0 0 1 1
BF ( . . 1.3):
' 1.3
) # 1 BF, < 4 . 2 $ ! - &
! - & 0 #. $
x2 x1 F0 f1 f2 f3 f4 f5 f6 f7 f8 f9 f10 f11 f12 f13 f14 f15
0 0 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1
0 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1
1 0 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1
1 1 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1
( . . 1.4), 9 =
: 4+$74.
' 1.4
$5#&94 6 5 % & 8 7#& &8 $ $- +) +
$# 7- . BF % - 7&-& 6 %6 -& & 1#$
> BF - --
BF
# - "-
+
$ % :
BF 05 !$ & 0 05 !$ & 1
1 2 3 4 5 6
- - + - +
- - - + +
f12=x2 - - - - -
f10=x1 - - - - -
+ - - + +
+ - - + +

34. 34
% 1.4
- + + - -
- + + - -
+ - + - +
+ - + + -
+ + + - +
+ + + - +
+ + + + +
+ + + + +
4+$74 BF, +
- BF, *
BF .
1.4.3 ) % $ # --4 5 # &8 ; -19 " ' 0 6 -&" 5$0&
+ : - BF
BF : BF.
) , =8 , = : BF, =
, ; 8 , =, 9
, 8 = , = 8
8 8 BF.
#
8 BF.
) 9 : , :
8 8
3' BF. / = = 8 .

35. 35
) 9 BF,
.
1.5 %& - 0$9 : 5 # &8 ; -19 "
1.5.1 % $"-$
" < = ; .
1. $ ;
AxAxAxAxA ∨∧∨∧=∧∨∧ ,
/ - - ’
2. $ ;
1211 xxxx =∧∨
$ ; = . $ =
: , 9
8 4 ($ 4). " = BF, :
4. ! ; =, 9
’ = - 88 .
8 4
8 4 . =
8 8 . ' 8 =
BF, 8 4, – ,
4 BF.
1.5.2 % $"-$– $1- #$ 1
" = :
. 4 :
1 . 4 BF 8

36. 36
2 . , 9 . & :
i-8 : i :
3 $ : . $
- ( )
4 $ , .
= .
! : 4
, .
1.5.3 % # "1$–) 9.1 !
" = 4 BF f 88 8 4.
= :
8 .
. : :
. ,/( BF f * ,
, " ,/( f.
1.5.4 % #. -$
" = 4 BF f 88 8 ' 8
8 . $ = : :
. /( BF f ,
" ,/( BF f
1.5.5 % ) &1$
" = :
= = 4
. $ = . ! =

37. 37
' 8 .
( ).
+ , : i-ro 8 = '
, , i-
. ' 8
= ' ' .
' 8 :
; 8 9 . + :
: ' ' , :
8 4.
1.5.6 % 1$ $ - - "'$
& 8
= . 1 – ( ) . ,
9 . + ; :
, ; .
= , %#: 1 = , 9
= , = 1. ! 0
: = .
( ) . . " = ; : 4
BF f 8 . . :
: 8 . .
$ & $ - . " ;
8 . & 8 =
: , 9 , :
= ' = , ; . ) 9 =
, :
' = , ; . .
2n
= n .

38. 38
: 8 ,
4, 4.
1.5.7 - 0$9 4 1 -’3-1 & -&8 - $#.-&8 ;
" 4 = 8
4 , ; : .
= , = 0
. . : = ' = 8.
, 0110 =
, , 0111 – , 1000 – .
! 8 4 = 8 4. 0
; = – ; 8 4 ( '
) : 8 4. 8
= , ; 8
4. & : : =
, – ;
+ ; 8 = ; . +
8 4 8 4:
1. $ ; :
2. $ ; 7 :
3. " 8 4 =
: 4 8 . % 8
8 4. + = :
: 8 4
.
, 4:

39. 39
18 4 :
4. ! . ; 8 4 =
, 4. . , 9
. 8,
8 . ( . . 1.2),
' . 1.2 – . ; 8 4
4 :
1.5.8 - 0$9 4 ; -19 " 5$0& $8 - $ -
4 8 « + » «; > » .
! ' BF ' 8 ' 8 :
,
, BF :
,

40. 40
; 8 BF
9 8 4 4. ,
8 « + » : , 9 : :
, /( BF f , BF f *
« % », /( '*
'* * % , *" " .
1.6 & : 41 - 0$9 : 5 # &8 ; -19 "
+ ,
, ' = : ,
= ; 8 88 8
8 8 BF : 8 ; 8 8 BF.
[27, 28, 34, 46, 52, 106], ,
= , . 8
:
1. SL – BF. = ,
8 BF. " 4
4+ = 8 4.
2. SAD – BF. . 4+ '"4+ =
’ BF. =
’= ( ’ –
4+, -/7& – '"4+)
3. SS – ; ’ 4+ '"4+.
4 , , 9 = . .
SS=2nSAD 4+ SS=nSAD '"4+, n –
4. SSH - BF, ’ 8
,

41. 41
5. SAC – 9 . .
= :
SAC=2nSSH 4+,
SAC=nSSH '"4+.
8 . .
$ 07
6. $ 07. =
, .
=
=
m
i
itt
1
7. , 9 . % =
- .
, 8 ,
.
% = 8
. % , , = ,
’ ’
. 9 ; =
-/7&.
8. + : $ 07. =
: , = :
, ’ : ,
, 9 : 8.
7 , 8 = : ; . ) 9
’ 8 8 = = , 8 :
’ : 8. . ;
’= 9
8.

42. 42
% , 8 8,
BF, = 8 8, 8
8 : 8.
+ , 9 8 8 BF
8 : 8 BF.
1.7 ) $- 1$ 0$ %$--4 %& $9 "- ! % # %7 --4
. - 6 % - ! %& $9 "- ! % # %7 --4
9 8
4+ – 8 (&'4+) BF, 8
, 9 = 9 8, :
4+, , 9 , 4+ = 4+
8 4+. 4+ :
(&'4+) =
: BF, 8 BF
4+ ( > ), 4+ ' -"
( ' ) 8 BF 8 4+;
&'4+ BF 3
8 : BF : ;
&'4+
BF, : 88 ;
; &'4+
88 : :
4+ ; = 8 8
;
4+ = 8
8 ;
4+ ; ; /
= 8;

43. 43
&'4+ =
8 =
8
' . 1.3 – 7 :
$ $ 0$%$' % # %7 -. = ; : 8 - 8
’
8
8 4+
BF
8 ; ( . . 1.3):

44. 44
1. 8 : 8 :
; 8 8 8
2. ' 8
, 9
3. + 8
8
: = ’ :
: , : 88
: .
& - 1& % 0% # 1
+
’ .
! ’
. .
8 8 8 , , ’
.
+ 8 8 . .
.
! ,
: ,
, = : .
& – 8
8
: 8 ' -" -
8 8 8
.

45. 45
+ , 9 ,
, 8 ' -"
, =
: .
& Cognate-
:
+
; 8.
& 8
. . , 9
+ : -
: .
& 8 : , –
" - , 7 –+ , , + ,
-. , ’ ,
#- ( /7&- (.
; 8 8 :
= SL, SAD, SS, SSH, SAC;
$ 07;
, 9 ,
: $ 07.
+ :

46. 46
( 2
+ ) * * (?
) ( ( * @ + ) *
+ ,
2.1 #$ &; 1$9 4 # - 6 - : - 7&-& 5 # &8 ; -19 " f(n)
2.1.1 5A - $--4 6 5 % & 1 $- : - 7&-& 5 # &8 ; -19 " f(n)
74 f(n), , %#. %# = ’=
: 8 BF, : %# = BF. %#
= : (2n
0 1), , ,
8 : L(n) BF (
n
2
2 ).
& , 9 : = : BF, = :
BF – : ( . . 2.1).
' 2.1
($# 7- . 1 #.1 BF L(n)
6 & 05 #.2 -- '& #$ $ ! -
>
66
#.1 .
$ ! -
BF (n)
#.1 .
4%1
BF
#.1 . BF L(n)
1 2 4 2 4
= 16
2 3 8 2 8
= 256
3 4 16 216
= 65.536
4 5 32 232
= 4.294.967.296
5 6 64 264
= G 1,84467·1019
! =8 , : = :
; ,
. ! ; 8 , : = :
BF, 8 ; 8 8 8 = 8 :
; , 9

47. 47
BF. % 9 : BF
= : BF : ,
’= BF, 9 = . &
: – ’ ,
’= ; BF 8 =
: : 8 : L(n) BF f(n).
. : 07 ,
, 8 8 8
[1], 9 BF 8 , 9
= 8 $ 07.
: : L(n) BF,
. 8 ; .
: : ; –
%# BF ; 8 ,
%#.
+ : ( 9
= BF) n! , :
8 – 2n
BF. % n : ,
: = : = .
: = 9 8 . + :
= , : = . /
BF : : , :
: (3'), : 88
= 8 : L(n)
BF.

48. 48
2.1.2 6$ #4 & - 41 - -&" 1 -&" 1 6 - - 6 - :
- 7&-& L(n) $ - $ %#4 --4 ! -$#.- : ; &
6 % $ # --4
2.1.2.1 ) -4 4 ! 6& #4 & -
$ : 8 : L(n) [2]
L(n) : BF,
= 8 . :
– (3') BF. 6
: =:
• BF – 3' 8
[3]: ( 4+),
8 (/4+), ' -" ('"4+),
(&'4+);
• 3' L(n) n ; , :
BF.
= BF %#
: 9 :
–
9 ;
8
. ; : : : :
• ; 0&9 8 ; –
;
• $ $ &9 : –
.
$ 2.1 0 ,
*

49. 49
% --4. BF fi %#. $
l . % l. + BF,
9 : 3', BF fi, =
%#:
• ;
•
+ ; = . .
%# %# 8 BF
%#. /
;
H% .
/ 2.1 8, 9
, :
. .2.2 BF 3' n.
' 2.2
($# 7- . 1 #.1 L(n) % '& #$ n
A
BF
BF L(n)
L(n)
1 2 24
= 16 5
2 3 28
= 56 24
3 4 216
= 65.536 402
4 5 232
= 4.294.967.296 1.228.158
5 6 264
G 1,84467·1019
400.507.806.843.728
. 3' : L(n)
– =8 BF : 8 3', , BF
+$ ( ).
BF, 10 +$ , [3]
L(n), : BF = , 9 =
– 8 . BF :
+$ – 2+$ , 10 +$ , 16 +$ .

50. 50
2.1.2.2 0$= 0$ -- . 8 8- '- " $# 0$9 : 5 # &8 ; -19 ", <
8 %4 . % 1#$% ! 6& #4 & -
/ BF, 9 : 3', =, 9
8 BF 8 ;
, 9 ; 8 .
= : =8 BF ; 8
3' .
BF, 9 3 , 3' A1 =
8 BF – BF f1, f2, f4, f8, f16, f32, f64, f128 ( . . 2.3). . BF
– 1.
' 2.3
BF, < 8 %4 . % 1#$% >1
! - & >> BF
x3 x2 x1 f1 f2 f4 f8 f16 f32 F64 f128
0 0 0 1 0 0 0 0 0 0 0
0 0 1 0 1 0 0 0 0 0 0
0 1 0 0 0 1 0 0 0 0 0
0 1 1 0 0 0 1 0 0 0 0
1 0 0 0 0 0 0 1 0 0 0
1 0 1 0 0 0 0 0 1 0 0
1 1 0 0 0 0 0 0 0 1 0
1 1 1 0 0 0 0 0 0 0 1
74 f128, 9 : 3', 8 = ( .
.2.1):
' .2.1 $ BF f128, 9 : 3' A1

51. 51
. = : , ; -
BF 3' ( , BF f128) – BF,
- ; BF, 9 : 3'.
8 8 8 8 BF
3' 8 BF
= ki.j. + = ki.j =
, , i – , j –
. ki.j : 0 1. ) 9 ki.j=1,
; = , 9 ki.j=0, .
) , - 8 8 BF, 9
3' BF f128, = ( . .2.2):
' .2.2 $ 8 BF 3' A1 BF f128,
ki.j = k-.j
=
= ( . . 2.4):
' 2.4
$5#&94 6 #4 &0$9 "-&8 - -&8 1 ; 9 =-
%#4 $# 0$9 : BF 0 >1 -$ - BF f128
6 #4 &0$9 "- !
- - ! 1 ; 9 =- $>
+ k1.1 k1.2 k1.3
f1 0 0 0
f2 0 0 1
f4 0 1 0
f8 0 1 1
f16 1 0 0
f32 1 0 1
f64 1 1 0
f128 1 1 1

52. 52
/ : ( . .2.1)
= ( . . 2.4) ; 8 8 BF
3'. ) , 8 BF, 8 =
, BF, BF,
8 = . 8 3' ; BF
f1 f128
2.1.3 1 6 0&9 4 ? -- -$ ! 6& #4 & -
2.1.3.1 5#& 1 - : 5 % & 5 # &8 ; -19 " -$ -
% 1 6 0&9 : ? -- -$
$ = 8
8 BF, 8 > , ' , + ,
/; , , ! , ' . 8
, 8
:
8 BF.
BF f(n), = ,
: « 9 » ( . .2.2):
' . 2.2 " BF « 9 »
BF > = BF i-
(1).
),...,,,...,(),...,,,...,(),...,,( 1111111021 niiiiniiiin xxxxQxxxxxQxxxxfy +−+− ∧∪∧== (2.1)

53. 53
: = ’ 8 i- ( 8 i-
) BF, 9 , i- . .
BF Qi0 Qi1 =, , : BF ( : , Qi0IQi1), 9
= n-1 .
8 BF i- , 8 BF
2 (1), BF ( . .2.2) =
( . .2.3):
' . 2.3 BF i-
! : BF, : 9
; :
• BF (Qi0=Qi1) – i-
, 9 = ;
• , BF = : (Qi0IQi1), 8
: ; BF Qi0, Qi1 : ; 8
74 f(n), : , : n -
. % 8 8 : n
BF Qi0 Qi1
+ : : BF
8 i- BF [5]
( . /), :

54. 54
$ 2.1. % i-
BF * BF Qi0 Qi1
$ 2.2. % BF, 1-,
** n BF Qi0 Qi1,
1-
' 2.2
BF, 9 1, 2 3 ( . .2.4). /
; BF
& :
: ; 8 BF .
' . 2.7 3 BF : BF 3',
BF BF
$ # % 1 0 # & 2.2 / 1-, BF f(n),
n BF Qi0(n-1) Qi1(n-1),
1-.
& = - ’ :
BF =
8 8 BF. # ; , : BF,
9 : 3', = n « » « » BF Qi0 Qi1, 9
: : 3', 9 88 .
: : BF 3'

55. 55
2.1.3.2 - &'-&" ; $1 $#.-&" 8$ $1 5 % & 5 # &8 ; -19 "
/ BF, : 8 . 2.2-2.3 = =
88 ; 8 . + BF f(x1, x2,…, xn) =
: BF Qi0(x1, x2,…, xi-1, xi+1, ,…, xn) Qi1(x1, x2,…, xi-1, xi+1, ,…, xn),
: .
. , 8
. : BF Qi0 Qi1, BF, :
, : 8 . 2.4, = :
BF f(n-1).
< . .
.
8
8 ( , ).
74 8 ; = . + 8
8 = . % ,
=
. ; ’
, ’
BF =:
• ;
• .
% 8, 8 8,
: 3 . ' ’ 8
BF = 8 8
. # ; , 8 BF
; = , 9
, 8.

56. 56
2.1.4 02& - ! 6& #4 & -
2.1.4.1 --4 02& -&8 ! 6 #4 & -
$ , 9 8 : L(n) BF f(n)
: 3' = , ; =
: BF . % ;
, ’= : 3'
: BF
$ 07 [2, 3, 4].
! 2.2 , 9 8 : L(n) BF f(n)
: 3' = , , : 3'
BF 8 : L(5) = ; 3497 . &
: 3' BF, ,
; = , 9 8 : L(n)
; , : ; = .
% 2.1 , 9 BF, 9 : 3'
. % , BF, 9 : 3',
.
: 3' ; : : ,
= : L(n), .
– .
& * p BF 0
BF.
) 9 BF f = l,
p=2n
-l
, 3' 1 BF f(4) 16 BF
( . . 2.5), : .

57. 57
' 2.5
1#$% - 1 %#4 BF f(4)
BF
10 )
-$ -&"
1 BF f
$!$ 5 -$ - !
1 $ BF f
$ 6 &
5 -$ - !
1 $ BF f
1 0000000000000001 1 15
2 0000000000000010 1 15
4 0000000000000100 1 15
8 0000000000001000 1 15
16 0000000000010000 1 15
32 0000000000100000 1 15
64 0000000001000000 1 15
128 0000000010000000 1 15
256 0000000100000000 1 15
512 0000001000000000 1 15
1024 0000010000000000 1 15
2048 0000100000000000 1 15
4096 0001000000000000 1 15
8192 0010000000000000 1 15
16384 0100000000000000 1 15
32768 1000000000000000 1 15
0 * ,
"
$ 2.3. 0 **
) 9 BF f(n), 9 : 3',
l1, = BF,
l2,
l1=2n
-l2,
, 9 BF : = 3'.
, . 2.6 : = 3' A 1 A 32767
BF f(4):

58. 58
% 2.6
$ 3' 1 32767 BF f(4)
> BF
10 )
-$ -&" 1
BF, l1=1, n=4
BF 10 )
-$ -&" 1
BF, l2=7, n=4
(l1=2n
-l2)
1 0000000000000001 65534 =65535-1 1111111111111110
2 0000000000000010 65533 =65535-2 1111111111111101
4 0000000000000100 65531 =65535-4 1111111111111110
8 0000000000001000 65527 =65535-8 1111111111111110
16 0000000000010000 65519 =65535-16 1111111111111110
32 0000000000100000 65503 =65535-32 1111111111111110
64 0000000001000000 65471 =65535-64 1111111111111110
128 0000000010000000 65407 =65535-128 1111111111111110
256 0000000100000000 65279 =65535-256 1111111111111110
512 0000001000000000 65023 =65535-512 1111111111111110
1024 0000010000000000 64511 =65535-1024 1111111111111110
2048 0000100000000000 63487 =65535-2048 1111111111111110
4096 0001000000000000 61439 =65535-4096 1111111111111110
8192 0010000000000000 57343 =65535-8192 1111111111111110
16384 0100000000000000 49151 =65535-16384 1111111111111110
32768 1000000000000000 32767 =65535-32768 1111111111111110
$ # % 1 0 # & 2.3. . L(n) f(n)
, * ,
’
$ : = 3' : L(3)
L(4) , 9 8 BF, 9
: 3', = l>2n-1
(
; : ), 4+
: l-2n
, = BF, 9 : 3',
= l-2n
. % = ’=
= 3' ; : , 9 =
BF %# :
9 :
–
9 ;
8 ;
8

59. 59
. ; : 3' ('3') ’= '3'
= 3'. + ’= = 3' '3' =
: ; : : : 2
( . . 2.7) : : L(n) BF f(n), ; 88
.
' 2.7
($# 7- . 1 #.1 L(n) % '& #$ n
A
BF
BF L(n)
L(n)
;
L(n)
1 2 24
= 16 5 4
2 3 28
= 256 24 14
3 4 216
= 65.536 402 238
4 5 232
= 4.294.967.296 1.228.158 740.192
5 6 264
G 1,84467·1019
400.507.806.843.728 267.206.412.342.126
$ 2.4. 0 , *
,
) 9 , 9 ’= : = ; ,
, = , 9 3', 1
0 : = ’= , 8 ; = 2
. , 8 : L(3) ’= : 3' '3' =
( . 17). ) , '3' 8
3', '3' ; 3', 22 : 3' =
13 : '3', 11 : .
2.1.4.2 ) 6 1 & & &1 & $--4 02& -&8 ! 6 #4 & -
! ; 8 : : 8 :
L(n) BF f(n) : 2 = 9 = : BF.
= :

60. 60
1. # : , = 3', : : ; 3', 8
; . BF 8
= ; ; ; 8 8,
: 8 : = 8 BF
2. / , '3', = ,
: : ; '3'
# = – 9 BF : =
, , ,
, = , 9 BF
; ,
, , , = .
! '3' = . $ :
= 3' :
• 3', l>2n-1
– : =
, ; ,
, 9 : 8
BF;
• & = 3'
;
• $ 8 = 3'
= .
% ,
; , 9 ,
+ = 3' 3' –
8 3', BF ; ,
= 8 8 3'
$ 2.2 % *
" BF

61. 61
% --4. BF fi, 9 n , BF
; .
. BF fi = l1 (l1<2n-1
), , ,
BF fi = p1=2n
-l1
) , = 8 BF fi = l2=p1
(l2>2n-1
), , , = 8 BF fi
= p2=2n
-l2=l1
3' : = ; BF, 9 : BF. !
2.1:
• 8 3' = – l1,
2n
-l1;
• = 8 3' = – 2n
-l1,
l1.
+ ; BF n2=n+m : BF
: 3' :
• 8 3' = – l1,
2n+m
-l1;
• = 8 3' = – 2n+m
-l1,
l1.
! BF = . % ,
9 : BF (l1=l1) :
= 8 3' (2n
-l122n+m
-l1)
H% .
= 3' =
8 3':
1. $ 8 3' ; 3',
l BF ; :
1
2
2
2 −
=≤ n
n
l ,
n – BF.

62. 62
+ ; n 3', 8 ,
; BF 3'.
2. 3', l BF ;
,
1
2
2
2 −
=> n
n
l ,
; n ; = ; :
l BF . ) ,
n = 3'. % , n=1
= 3', 9 '3' = 3' 0J3, n=2
= 3', 9 '3' = 3' 0J15, n=3
= 3', 9 '3' = 3' 0J255.
= 3' = 3',
l BF ;
.
/ , n=3, 3' 127 (l=7>23-1
=4) = 3' 1
+ ; n 8
= 3'.
8 3' BF, 9 1, 2, 3
, ( . . 2.7) ( . . 2.8
' . 2.8. = 3'
: BF

63. 63
2.1.5 !$-! 6& #4 & -
: '3' , 9 : '3'
: BF –
. ! f(n) : 0 2n
.
: = ; , :
: BF (
n
2
2 )
% ’= : 8
: L(n) BF f(n) = : - ("3') BF.
"3' = : , ’= = '3', "3' 8 : L(n)
BF f(n) 1
2
2
2 −
= n
n
: . . "3' , 9 =
BF 0 2n-1
.
. 9 : 8 : L(n) BF f(n)
= ( . 2.9)
' 2.9
0 #. $ & < #.- --4 - 7&- BF 2#48 &1 & $--4
#.1 .
$ ! -
BF, (n)
#.1 . BF . !
L(n)
#.1 . #.1 . #.1 .
2 16 5 2 2
3 256 24 13 4
4 65536 402 238 8
. : 8 : L(n) BF f(n)
9 L(n) 12
1
2
2
2
2 +−
−
= n
n
n
n
– = ,
: BF
2.1.6 $0 $ 1 $ 6 - : - 7&-& L(n) 8 5 # &8 ; -19 " f(n)
% , ’= BF 8
: 8 : L(n) BF f(n), 9 =
[4]:

64. 64
1. $ 8 : L(n) BF f(n) =
. + : L(n) BF f(n) = "3', "3' – '3',
'3' – 3', 3' – BF.
2. : 8 , 9
; BF, 9 : :
3. : : 9 = : :
( )
. = : : BF, :
BF 8 = , 9 = 9 =
8 : BF.
2.2 ! -$#.-$ ; $ 6 % $ # --4 41 02& - 6 & 0 $-
0$!$#.- --4 - 3'&8 ; 6 % $ # --4 5 # &8 ; -19 "
2.2.1 5#& ; -19 -$#.- 6 -&8 & 5 # &8 ; -19 "
! -$#.-$ ; $ 6 % $ # --4
4+$74 = BF, : -
BF, 9 : : L(n) BF. 8
4+$74 8 8 . : 3',
, =, 9
: 8 3' = 4+$74. / 4+$74 =
. : = 3', =
.
# BF = BF,
8 = BF. : BF =
4+$74 8. ) , BF, 9
, : =
. & = BF
(4+ $74), = ; ,

65. 65
: , : - 8 8 BF. 4+ $74 BF, 9
, = 4+$74,
BF
8 BF
8 BF.
) 9 : , :
8 8
3' BF. / = = 8 . / 9
BF,
.
%
8 – 4+ $74.
2.2.2 % $ 5 # : ; -19 : ! -$#.- " ; 6 % $ # --4
& BF :
1) BF.
% , ( 4+),
' -" ('"4+) 8
(/4+) = : &'4+;
2) : 8
> ' ;
3) = 8 – 4+ $74;
4) = BF, BF, 9
: 3'
5) 8 BF &'4+ :
, . 0 = :
8 8
$ : : , :
+ , 9

66. 66
BF, 9 = 8 BF, 2 ’
.
+ ; – . .
= , %# BF ; ,
; , :
; = . . &'4+
: BF, 9 : 1-31. ! 8 ,
&'4+ ; BF, 9 : 1-31 =
, BF 1f – + BF 8f ( 2 , BF –
1-31) – ’ .
8 BF ( . . 2.2)
&'4+ ( . . 2.5):
' . 2.5 + &'4+
– ’= . & ’=
, : BF, , : :
• ’= , 9 BF 1 , %# BF
; , , :
; =
. . ’= &'4+
: BF, 9 : 1-, 1-31 - 11-3 . !
8 , ’= &'4+ ; BF,
9 : 11-3 = , BF 87 ff = - ;
> BF 114 ff = - ’ ;
• ’= , 9 BF 2 , %# BF
0 1,

67. 67
;
• ’= , 9 BF 3 , =
( )
8 BF ( . . 2.2)
&'4+ ’= ( . . 2.6).
BF y=f(x1,x2,x3,…,xn) &'4+
' (1), : = : 4i –
BF f(k) (0EkEn) Qi(n-k) – (2.2).
i
i
(Qy
k
⋅∪=
−
=
12
0
(2.2),
' . 2.6 + &'4+
’=
+ 8 BF &'4+ :
1. + . 7 - :
.
2. + = . = =
. = =
. %
= = 8 8
8, =
, = =1 = 2
, : = - i-
n : (2.3).
),...,,,...,(),...,,,...,( 11111110 niiiiniiii xxxxQxxxxxQxy +−+− ∧∧= (2.3)
)x,...,x,x,...,x(Q)x,...,x,x,...,x(Qy n1i1i11in1i1i10i0i 1i +−+− ∧∧= ΦΦ

68. 68
) 9 BF, . 2.5, =1 BF
&'4+ = ( . .2.7):
' . 2.7 " 8 8 BF i- &'4+
BF )1(0 −nQi )1(1 −nQi
$ ’=
BF &'4+. = BF :
8. # BF Qi0 Qi1 = BF, 9
, . $ : , Qi0IQi1,
; = BF .
. BF Qi0 Qi1 = : BF, 9 n-1 . 7 -
BF : - j-
(2.4). $ = , 9 ’
BF, :
),...,,,...,(),...,,,...,,,...,(
),...,,,...,,,...,(),...,,,...,(
)),...,,,...,,,...,(),...,,,...,,,...,((
11111111110
11111001111
11111101111100
niiiinjjiijiji
njjiijijiniiii
njjiijijnjjiijiji
xxxxQxxxxxxxQxx
xxxxxxQxxxxxxQx
xxxxxxQxxxxxxxQxxy
+−+−+−
+−+−+−
+−+−+−+−
∧∨∧
∨∧=∧∨
∧∨∧∧=
(2.4)
)x,...,x,x,...,x(Q
)x,...,x,x,...,x,x,...,x(Q)x,...,x,x,...,x,x,...,x(Q
)x,...,x,x,...,x(Qx
))x,...,x,x,...,x,x,...,x(Qx)x,...,x,x,...,x,x,...,x(Qx(xy
n1i1i11i1i
n1j1j1i1i11j0i1j0in1j1j1i1i10j0i0j0i
n1i1i11ii
n1j1j1i1i11j0ijn1j1j1i1i10j0iji
+−
+−+−+−+−
+−
+−+−+−+−
∧∨
∨∧∨∧=
=∧∨
∨∧∨∧∧=
Φ
ΦΦ
. 8 BF 3 . . &'4+ BF :
, = ( . .2.8).

69. 69
; Qi1j0 Qi1j1 = =2,
Qi0 – =1. / : ,
=3,4,5,...,n.
' . 2.8 " 8 BF &'4+ i- j-
# BF = 8 BF. " BF
&'4+ = ; 8
' . 2.9 " 8 =n BF &'4+
( )

70. 70
8
= =n BF &'4+
: , = ( . .2.9)
8 4+ ,
; , :
= ( –
= , BF,
– BF ),
8 8 BF = .
8
= =n BF &'4+ 8
: , =
( . .2.10):
' . 2.10 " 8 =n BF &'4+
8
(7 )

71. 71
$ = 8 =
’= . $ : BF , 9
BF, 9 , ,
’= = . + ;
= . ) 9 , : BF f(n) =
8 n BF f(n-1). ) , : 8
74 f(n-1) : ,
’= . % 8
BF, 9 , = ( . .2.11).
' . 2.11 7 BF &'4+

72. 72
. ; =
; = ,
: . 2.18.
2.2.3 $0& -&" 1 ; 9 =- – 1#3' &" 6 1$0-&1 ; $--
6 & $#.- : ; & 5 # &8 ; -19 " ! -$#.- " ;
6 % $ # --4
: =
8 BF , 9 = = =8
BF, : . & = ,
8 = . =
; 4i – , – .
, 8 (3) Qi0j0=1, Qi0j1=0.
(2.4) :
)x,...,x,x,...,x(Q)x,...,x,x,...,x(Qxxx
)x,...,x,x,...,x(Qx0xx1xx)x,...,x,x,...,x(Qx
)x,...,x,x,...,x,x,...,x(Qxx)x,...,x,x,...,x,x,...,x(Qxxy
n1i1i11i1i0j0in1i1i11iiji
n1i1i11iijijin1i1i11ii
n1j1j1i1i11j0ijin1j1j1i1i10j0iji
+−+−
+−+−
+−+−+−+−
∧∨=∧∨=
=∧∨∧∨∧=∧∨
∧∨∧=
ΦΦ
(2.5)
% = = ,
8 ; BF,
= (2.3),
= [13].
$ 2.3 0 * " ,
, "
" " * '*
, * * * +(
% --4. ! 8 ' 8 8
(" 4) 8 BF = ' , 9
: : . : BF

73. 73
: =8 " 4. .
" 4 = = : –
; : .
BF n . . =
BF (2.3) , 9 ; ii QQ 10 ≠ :
iiii QxQxy 10 ∧∨∧= (2.6)
& ii QQ 10 ≠ xi2xi, : :
= . . ;
8.
) 9 : 1=iQ ,
8 ;
= ; . . ,
= KK = , : =
8, .
) 9 : 0=iQ ,
– .
) 9 : 1≠iQ 0≠iQ ,
: BF n-1
88 j- ( niij ,...,1,1,...,2,1 +−= ). ) 9
jiji QQ 10 = , j- : ( =
, : BF) –
1=∨ jj xx , ijQ : :
BF ; n-2 .
) 9 8 Qj02Qj1, =
, : = =
BF
+ 8 :
, = : :
− 1... =kijQ ;

74. 74
− 0... =kijQ ;
− :
i...k(
. BF , =
= : , : :
, , , " 4 BF
H% .
:
1. ! = rK = : BF, r –
( ) 8 i...k(
2. + : +( 8 BF = 88 :
4
) 9 BF 8 , , 9
8 BF = = 8.
, 9 BF, : 8
.
$ 2.5 , * ,/(
* BF (%
"
"
% --4. BF : :
8 8 4. . = ; ,
; ,
BF &'4+ : =
8, ; .

75. 75
& 8 BF ; 8 BF :
8. + = ,
4. $ , 9
8 : BF L(3) – G0,4%, L(4) – G1,67%, L(5) – G3,37%.
% , =. +
8 97-99%
: : n 8
: L(n) BF. : 8 , 9 : :
1) 8 BF;
2) =
% : L(n) BF = ,
=
= . . = . +
8 = ; .
H% .
+ 8 BF f(n) = 8
:
2) = =1 K z1=1L2Ln=2Ln : ;
3) = =2 K
)1(2
2
)1())1(1(4
)12...)3()2()1((2122 −⋅⋅=
−⋅−+⋅
=+++−+−+−⋅⋅⋅= nn
nn
nnnz
: ;
4) = =3 K
=⋅⋅⋅+++++−+−⋅⋅⋅++++−+−⋅⋅⋅⋅⋅= )1212...)12...)4()3((212)12...)3()2((212(2(23 nnnnz
)12...)3()2()2()1((8)12...(16
3
1
4
1
2
1
+++−⋅−+−⋅−⋅=+++++⋅=
−
=
−
=
−
=
nnnniii
n
i
n
i
n
i
: ;
5) . . =n;

76. 76
: zi ; =
= , En/2, >n/2 ; = . %
BF f(5) : zi :
• =1 K z1=10;
• =2 K z2=40;
• =3 K z3=80;
• =4 K z4=80;
• =5 K z5=32;
) 9 = ,
: zi = ; :
.
2.2.4 6#& 6 #4 &0$9 : 8 %-&8 &!-$# 6 & - 0$9 : 5 # &8 ; -19 "
! -$#.- " ; 6 % $ # --4
. 8 BF &'4+ ( . . 2.8-2.10) =
ix~ , . 4+ =
8 n n , 9
; = ; '"4+ (
' " ) /4+.
&'4+ n n
+ = &'4+ 8
,
( ). 9 = 8
BF = :
1. + : ;
( ). . = ;
( . . 2.9-2.11), 9 9
= 8. 9

77. 77
= 8, = ’=
.
$ 8
= ( . . 2.10).
. 8 ;
; , 9 : 3', 8 BF
&'4+ : 30% ; ;
07, : .
' 2.10
; 1 & - . 0$ $--4 6 #4 &0$9 : 8 %- : 2&-& %$-&8
2#48 - : 8 %-&8 %$-&8
#.1 .
$ ! -
BF, (n)
#.1 .
BF . !
L(n)
0 $8 --
1
0-$' --4
SAD
(-$' --4
SAD
-$ # % 1
6 #4 &0$-
9 : 8 %- :
2&-&
; 1 & -
- .
6 #4 &0$-
9 :, %
0 $8 --
1
0-$' --4
Ss
(-$' --4
Ss
-$ # % 1
6 #4 &0$-
9 : 8 %- :
2&-&
; 1 & -
- .
6 #4 &0$-
9 :, %
3 256 1024 684 33,2 3072 22052 33,2
2. > ; , 9 :
3'. = : ; ;
: ; 8 .
9 = 8,
= ’= ; .
$ 8
= ( . . 2.11):
' 2.11
; 1 & - . 0$ $--4 6 #4 &0$9 : 8 %- : 2&-& %$-&8 2#48
0$ -& %-&8 &5& $3'&8 # ! '-&8 # - -$ -2 , < -$# 7$ . %- "
#.1 .
$ ! -
BF, (n)
#.1 .
BF . !
L(n)
0 $8 -1
0-$' --4 Ss
(-$' --4 Ss
-$ # % 1
6 #4 &0$9 :
8 %- : 2&-&
-.
& - --4
%
6 '$ 1 !
$-
; 1 & - .
6 #4 &0$9 :,
%
3 256 4524 2297 0,70 30
4 65536 2682312 1737661 0,71 29

78. 78
. 8 ;
; , 9 : 3', 8 BF &'4+
: 30% ; ; 07,
: .
2.2.5 - 0$9 4 BF +) 0 1 ' --4 $5 %&; 1$9 =3
-; $9 "-&8 '$ &- '# - 4%
/ 8 BF &'4+
, :
1. . 8 BF &'4+
, : . 2.2. &
8 = 1-1. & , =
8, = : .
- 8 8 8 : L(n) BF n
n
21
2 −
= = ;
( . . 2.12)
% 2.12
- . 1 ' --4 -; $9 "-&8 '$ &- %#4 6 - : - 7&-& L(n)
8 &--&8 BF
>
66
#.1 . $ ! -
&-- " BF
#&'&-$ " - 1 ' --4
-; $9 "- : '$ &-&
1 1
0,50
2 2
0,125
3 3
0,007 812 5
4 4
0,000 030 517 58
5 5
4,65661*10-08
6 6
1,0842*10-17
2. , 9 = ,
, 9 , 9
= 8 = SAD (

79. 79
) 4 = SL, 9
= 8.
; 8 =
, 9 , : 8
; . ) ,
= ; = K
8 8 BF ( . 2.10 .2.11) 8
& - 1& % 0% # 2
! : 8 8
: 8 : L(n) BF f(n) = ,
; 8
8 8. & 8 8 = 88
= ’ : , 9 = ;
: : 9 , 9 =
; 8 8 BF
8 > .
' = 8 :
= : , 9 5 = 8:
: f(n);
- BF;
; BF;
BF;
BF.
. 8 8 : =
: : BF : BF 8
.

80. 80
. : :
: : 8 : ,
: . ! =
3' BF 8 8
, 9 : : : 9
8 :
7
= : , 9 ; ;
– : BF f(n), 9 : 3', = = 8
8 n BF f(n-1), 9 :
: 8 :
8
;
. & = BF
8 > ' , 9 =
BF = BF. :
BF =
( 3' A1), 9
’= ; , .
8 –
= , 9 = = 8
8
" [1, 2, 3, 4, 5, 9, 10, 19, 20, 21, 23, 25, 28, 30]

81. 81
'&! #2 3
( , + ,
+ ) *
3.1 5A - $--4 % - 0$9 : 5 # &8 ; -19 " ! -$#.- " ;
6 % $ # --4
& = 8
= 8 BF – BF .
. 8 BF &'4+ : 8 BF
f(n). + = BF f(n) 8 8
(2.3), : BF fi0(n-1)
fi1(n-1). 8 , 9
= .
+ BF, (2.3),
, : : : 9 . =
8 BF &'4+ = – = K .
BF = , 9 BF
= K . ! K 8
= .
: 8:
1. . 8 BF fi0(n-1) fi1(n-1)
: 0 1. - 9
: L(n) BF f(n)
n
n
21
2
2
2
2 −
= . .
BF f(n) .
2. BF fi0(n-1) fi1(n-1) = 1. .
BF : BF f(n-1), 9
8.

82. 82
3. BF : , =
BF fi0(n-1) fi1(n-1)
) 9 BF , ;
BF fi0 fi1, BF, 9
= 0+, , ’ :
8 ( 2.8). .
; 2 . % = , , ,
; .
) 9 ' , ’=
' – &'4+ – 4+.
, 9 4+ = ; :
&'4+.
) 9 ’ , ’=
-/7& – ; &'4+ –
' -" 4+.
) 9 ’ , ’=
, = ( / ) –
; &'4+ – 4+.
. 8 BF &'4+ ’ –
; : 8 BF, 9
.
) 8 BF &'4+ 8
8 8 BF, 9
, . =
2.2 2.3.
3.2 - 0$9 4 6 - 3 &0-$' -&8 5 # &8 ; -19 " ! -$#.- " ;
6 % $ # --4 2#48 1 ' --4 -; $9 "-&8 '$ &- '# - 4%
" 8 8 BF (PO BF) &'4+ ;
= 8 4

83. 83
4+ : &'4+ [13]. .
8 &'4+ 8 BF. .
8 BF &'4+, , 8 , BF
= 2 ( . . 2.2).
= BF.
+ ; : 8
; , iQ BF –
BF : . + BF :
:
1) . . 4/2
00 =∧x
= . .
: =
2) . . 4/2
xx =∧1
= iΦ BF. %
2.2 = = ,
: ; 8. .
: =
3) , =
. . 8
8 8 8 –
(
2 ).
9 8 BF :
8 BF. + = :
1. BF = 8 8
. . , = :
: 8. % =
8, BF = .

84. 84
. ; 8 BF ,
= K
;
2. . , 9 : BF, ,
8 = BF . %
: ,
, 9 =
K . + 8
:
8
3. # (2.2) =, , :
. % , 8 , =
8 BF . " :
8 : , ’
8 ,
.
: 8, =
, : " 4 BF:
1. ) < 8 BF &'4+,
BF = . . = .
: = (
). ) , :
. & 9
; 8 = 8. +
8 ;
= : BF
2. + i- 8. + :
8 BF = 8 BF, 9 , ,
; 8 BF. +
8 BF BF 9 : 8 :

85. 85
. + 8
i- 8, 9
. 8 = ; 8 BF
3. + 8. . ,
, : 8. +
= 8 4/2, , ,
BF. + 8
8.
= , ;
8 BF, 8 BF 8
8 , , 8 BF &'4+ –
8 8. 8 8 BF &'4+
; 8 ;
=
K=1. – K=2, – K=3, . . n-
– K=n. + = , 9 :
. = ; =
: : .
& '= 8 8 =
(TI) BF 88 8.
+ ; 8 8 :
:
1. > ; = 0 n [6].
.
8 8 ;
=
, =
iΦ ,
= KK = . + 8 BF = ;
TI BF

86. 86
2. > ; = n 0 [18].
. 8
8 ; ; =
« ; » 8
;
= KK = . + 8 BF = ;
TI BF
3. " 8 8 [19]. ; =
;
: ; 8 = 8 :
1. & ’= : 8 8 = TI
BF. + : 8 ; ;
=
2. & 8 8 ’
3. 8 : BF
, : BF
4. 8 8 –
8 =
5. . 8 ; ; = ; ;
BF, 9 8, ,
8 ; ; = ; ;
BF, : 8
6. . 8 ; ; = :
; BF (
), , 8 ; ;
= : BF
( ) BF
( )

87. 87
7. ! ; = 8 ;
; = , = :
; ’ , 9 , = :
,
; ,
:
: 9 8
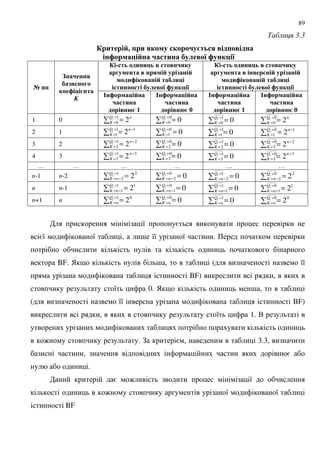
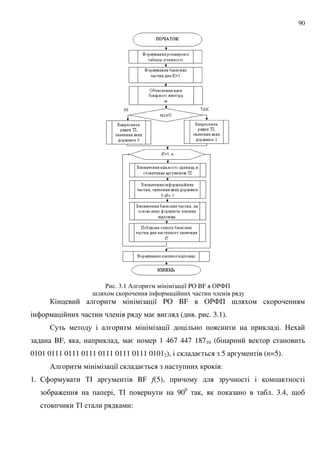
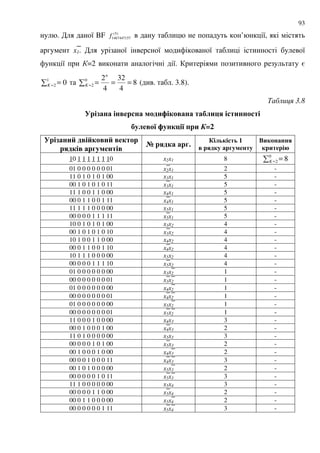
3.3 - 0$9 4 6 - 3 &0-$' -&8 5 # &8 ; -19 " % 6$ $# #.- :
% 1 6 0&9 : 2#48 05 #.2 --4 0-$' --4 1 ; 9 =- $
" 8
8 ; ; = 88 " 4
= ; %# BF [6].
' 3.1
($%$--4 BF %&; 1 $- 3
x4 x4 x3 x3 x2 x2 x1 x1 y
0 0 1 0 1 0 1 0 1 0
1 0 1 0 1 0 1 1 0 1
2 0 1 0 1 1 0 0 1 0
3 0 1 0 1 1 0 1 0 1
4 0 1 1 0 0 1 0 1 0
5 0 1 1 0 0 1 1 0 0
6 0 1 1 0 1 0 0 1 0
7 0 1 1 0 1 0 1 0 0
8 1 0 0 1 0 1 0 1 1
9 1 0 0 1 0 1 1 0 0
10 1 0 0 1 1 0 0 1 0
11 1 0 0 1 1 0 1 0 0
12 1 0 1 0 0 1 0 1 1
13 1 0 1 0 0 1 1 0 0
14 1 0 1 0 1 0 0 1 1
15 1 0 1 0 1 0 1 0 1
; 8 = : =8 BF , ;
. :
8 8 ,

88. 88
%# BF. " BF =
8 %# BF , 9 %# BF
8 , , BF ( .
. 3.1). %# BF, 9 =
1101000100001010. :
BF K=1. . «1»
. &
= 8
8 .
8 BF : K=1 =
, ( . . 3.2).
' 3.2
$0& -$ -; $9 "-$ '$ &-$ 6 & K=1
%#4 BF 1101000100001010
A
7 #
1 x4 11010001
2 x4 00001010
3 x3 11010000
4 x3 00011010
5 x2 11000010
6 x2 01010010
7 x1 10000011
8 x1 11010000
/ K=2,
= 8 = ’ 8, K=3 –
= ’ 8, K=n – ’ 8, 9 n
. +
= ; = 2
$ 8 =
8 8 , =
, = 0 1 ( . . 3.2).

89. 89
' 3.3
& ", 6 & 41 1 ' = . 4 %6 %-$
-; $9 "-$ '$ &-$ 5 # : ; -19 :
- . %&-&9. 6'&1
$ ! - $ 6 4 " 0$- "
%&; 1 $- " $5#&9
&-- 5 # : ; -19 :
- . %&-&9. 6'&1
$ ! - $ - - " 0$- "
%&; 1 $- " $5#&9
&-- 5 # : ; -19 :> 66
(-$' --4
5$0& - !
1 ; 9 =- $
K
-; $9 "-$
'$ &-$
% -3= 1
-; $9 "-$
'$ &-$
% -3= 0
-; $9 "-$
'$ &-$
% -3= 1
-; $9 "-$
'$ &-$
% -3= 0
1 0 =
= =1
0 2iQ
K
n =
= =0
0 0iQ
K
=
= =1
0 0iQ
K
=
= =0
0 2iQ
K
n
2 1 =
=
−
=1
1
1
2iQ
K
n =
= =0
1 0iQ
K
=
= =1
1 0iQ
K
=
=
−
=0
1
1
2iQ
K
n
3 2 =
=
−
=1
2
2
2iQ
K
n =
= =0
2 0iQ
K
=
= =1
2 0iQ
K
=
=
−
=0
2
2
2iQ
K
n
4 3 =
=
−
=1
3
3
2iQ
K
n =
= =0
3 0iQ
K
=
= =1
3 0iQ
K
=
=
−
=0
3
3
2iQ
K
n
… … … … … …
n-1 n-2 =
−= =1
2
2
2iQ
nK
=
−= =0
2 0iQ
nK
=
−= =1
2 0iQ
nK
=
−= =0
2
2
2iQ
nK
n n-1 =
−= =1
1
1
2iQ
nK
=
−= =0
1 0iQ
nK
=
−= =1
1 0iQ
nK
=
−= =0
1
1
2iQ
nK
n+1 n =
= =1 0
2iQ
nK
=
= =0
0iQ
nK
=
= =1
0iQ
nK
=
= =0 0
2iQ
nK
8 =
=8 8 , ; 88 8 . +
BF. ) 9 ; , ( 88
BF) ,
8 0. ) 9 ; ,
( 88 BF)
, 8 1. .
: . ! = , 3.3,
, =
.
= : 8
: 8 8
BF

90. 90
' . 3.1 / 8 PO BF &'4+
;
8 PO BF &'4+ ;
= ( . . 3.1).
$ 8 .
BF, , , = 1 467 447 18710 (
0101 0111 0111 0111 0111 0111 0111 01012), = 5 (n=5).
/ 8 = :
1. $ %# BF f(5),
: , %# 900
, . 3.4, 9
%# :

91. 91
' 3.4
$ ! - BF f(5) %#4 - 0$9 : BF +)
"1 &" 1 % 4%1 $ ! - > $ !.
1010 1010 1010 1010 1010 1010 1010 1010 x1
1100 1100 1100 1100 1100 1100 1100 1100 x2
1111 0000 1111 0000 1111 0000 1111 0000 x3
1111 1111 0000 0000 1111 1111 0000 0000 x4
1111 1111 1111 1111 0000 0000 0000 0000 x5
2. + %# BF ;
, . 3.5
. = BF =1
' 3.5
%&; 1 $-$ %#4 - 0$9 : BF +)
"1 &" 1 4%1 $ ! - > $ !.
1010 1010 1010 1010 1010 1010 1010 1010 x1
0101 0101 0101 0101 0101 0101 0101 0101 x1
1100 1100 1100 1100 1100 1100 1100 1100 x2
0011 0011 0011 0011 0011 0011 0011 0011 x2
1111 0000 1111 0000 1111 0000 1111 0000 x3
0000 1111 0000 1111 0000 1111 0000 1111 x3
1111 1111 0000 0000 1111 1111 0000 0000 x4
0000 0000 1111 1111 0000 0000 1111 1111 x4
1111 1111 1111 1111 0000 0000 0000 0000 x5
0000 0000 0000 0000 1111 1111 1111 1111 x5
3. . 3.5 ; BF – BF 2 +$ (
BF) ( . . 3.6)
' 3.6
%&; 1 $-$ $5#&94 &--
"1 &" 1 4%1$ BF
0101 0111 0111 0111 0111 0111 0111 0101 )5(
1467447157f
"1 &" 1 4%1 $ ! -
1010 1010 1010 1010 1010 1010 1010 1010 x1
0101 0101 0101 0101 0101 0101 0101 0101 x1
1100 1100 1100 1100 1100 1100 1100 1100 x2
0011 0011 0011 0011 0011 0011 0011 0011 x2
1111 0000 1111 0000 1111 0000 1111 0000 x3
0000 1111 0000 1111 0000 1111 0000 1111 x3
1111 1111 0000 0000 1111 1111 0000 0000 x4
0000 0000 1111 1111 0000 0000 1111 1111 x4
1111 1111 1111 1111 0000 0000 0000 0000 x5
0000 0000 0000 0000 1111 1111 1111 1111 x5

92. 92
4. + , ; BF )5(
1467447157f . .
10 22 . %
; , 8
8, ; ,
= ;
. + ; (
= K=1), = , 9
= – = =
= =1
1 0iQ
K , = , 9
= – = ( . . 3.3):
=
= ===0
1 16
2
32
2
2iQ
K
n
. = , 9 x1 ( . . 3.7) = ’ ,
= .
' 3.7
0$-$ - -$ %&; 1 $-$ $5#&94 &--
5 # : ; -19 : 6 & =1
0$-&" % "1 &" 1 4%1$ BF
00 0 0 0 0 0 0 00 )5(
1467447157f
0$-&" % "1 &" 1 4%1
$ ! -
#.1 . 1
4%1
$ ! -
&1 -$--4
1 & 3
11 1 1 1 1 1 1 11 x1 10 -
00 0 0 0 0 0 0 00 x1 0 = =1
1 0K
10 1 1 1 1 1 1 10 x2 8 -
01 0 0 0 0 0 0 01 x2 2 -
11 0 1 0 1 0 1 00 x3 5 -
00 1 0 1 0 1 0 11 x3 5 -
11 1 0 0 1 1 0 00 x4 5 -
00 0 1 1 0 0 1 11 x4 5 -
11 1 1 1 0 0 0 00 x5 5 -
00 0 0 0 1 1 1 11 x5 5 -
8 8 =2. ' = 8 ' ,
9 2 = , , 9
=1 , 9

93. 93
. 8 BF )5(
1467447157f ’ 8,
x1. 8 8 8 8
8 =2 8. =
= =1
2 0K = ===0
2 8
4
32
4
2
K
n
( . . 3.8).
' 3.8
0$-$ - -$ %&; 1 $-$ $5#&94 &--
5 # : ; -19 : 6 & =2
0$-&" % "1 &" 1
4%1 $ ! -
> 4%1$ $ !.
#.1 . 1
4%1 $ ! -
&1 -$--4
1 & 3
10 1 1 1 1 1 1 10 x2x1 8 = =0
2 8K
01 0 0 0 0 0 0 01 x2x1 2 -
11 0 1 0 1 0 1 00 x3x1 5 -
00 1 0 1 0 1 0 11 x3x1 5 -
11 1 0 0 1 1 0 00 x4x1 5 -
00 0 1 1 0 0 1 11 x4x1 5 -
11 1 1 1 0 0 0 00 x5x1 5 -
00 0 0 0 1 1 1 11 x5x1 5 -
10 0 1 0 1 0 1 00 x3x2 4 -
00 1 0 1 0 1 0 10 x3x2 4 -
10 1 0 0 1 1 0 00 x4x2 4 -
00 0 1 1 0 0 1 10 x4x2 4 -
10 1 1 1 0 0 0 00 x5x2 4 -
00 0 0 0 1 1 1 10 x5x2 4 -
01 0 0 0 0 0 0 00 x3x2 1 -
00 0 0 0 0 0 0 01 x3x2 1 -
01 0 0 0 0 0 0 00 x4x2 1 -
00 0 0 0 0 0 0 01 x4x2 1 -
01 0 0 0 0 0 0 00 x5x2 1 -
00 0 0 0 0 0 0 01 x5x2 1 -
11 0 0 0 1 0 0 00 x4x3 3 -
00 0 1 0 0 0 1 00 x4x3 2 -
11 0 1 0 0 0 0 00 x5x3 3 -
00 0 0 0 1 0 1 00 x5x3 2 -
00 1 0 0 0 1 0 00 x4x3 2 -
00 0 0 1 0 0 0 11 x4x3 3 -
00 1 0 1 0 0 0 00 x5x3 2 -
00 0 0 0 0 1 0 11 x5x3 3 -
11 1 0 0 0 0 0 00 x5x4 3 -
00 0 0 0 1 1 0 00 x5x4 2 -
00 0 1 1 0 0 0 00 x5x4 2 -
00 0 0 0 0 0 1 11 x5x4 3 -

94. 94
. ; x2x1 = –
= 0.
5. ' = 8 ' , 9 2 =
, , 9 =1
, 9 .
8 BF )5(
1467447157f ’ 8,
x1. 8 8 8 8
8 =2 8. =
= =1
2 0K = ===0
2 8
4
32
4
2
K
n
( . . 3.8). . ;
x2x1 = – = 0.
6.
%# BF =3, = = =1
3 0K
= ===0
3 4
8
32
8
2
K
n
( . . 3.9). . ’
x4x3x2 , x5x3x2, x4x3x2, x5x3x2, x5x4x2, x5x4x2 = ’
' 3.9
0$-$ - -$ %&; 1 $-$ $5#&94 &--
5 # : ; -19 : 6 & =3
0$-&" % "1 &" 1
4%1 $ ! -
> 4%1$ $ !.
#.1 . 1
4%1 $ ! -
&1 -$--4
1 & 3
1 2 3 4
01 0 0 0 0 0 0 00 x3x2x1 1 –
00 0 0 0 0 0 0 01 x3x2x1 1 –
01 0 0 0 0 0 0 00 x4x2x1 1 –
00 0 0 0 0 0 0 01 x4x2x1 1 –
01 0 0 0 0 0 0 00 x5x2x1 1 –
00 0 0 0 0 0 0 01 x5x2x1 1 –
11 0 0 0 1 0 0 00 x4x3x1 3 –
00 0 1 0 0 0 1 00 x4x3x1 2 –
11 0 1 0 0 0 0 00 x5x3x1 3 –
00 0 0 0 1 0 1 00 x5x3x1 2 –
00 1 0 0 0 1 0 00 x4x3x1 2 –
00 0 0 1 0 0 0 11 x4x3x1 3 –
00 1 0 1 0 0 0 00 x5x3x1 2 –
00 0 0 0 0 1 0 11 x5x3x1 3 –

95. 95
% 3.9
1 2 3 4
11 1 0 0 0 0 0 00 x5x4x1 3 –
00 0 0 0 1 1 0 00 x5x4x1 2 –
00 0 1 1 0 0 0 00 x5x4x1 2 –
00 0 0 0 0 0 1 11 x5x4x1 3 –
10 0 0 0 1 0 0 00 x4x3x2 2 –
00 0 1 0 0 0 1 00 x4x3x2 2 –
10 0 1 0 0 0 0 00 x5x3x2 2 –
00 0 0 0 1 0 1 00 x5x3x2 2 –
00 1 0 0 0 1 0 00 x4x3x2 2 –
00 0 0 1 0 0 0 10 x4x3x2 2 –
00 1 0 1 0 0 0 00 x5x3x2 2 –
00 0 0 0 0 1 0 10 x5x3x2 2 –
10 1 0 0 0 0 0 00 x5x4x2 2 –
00 0 0 0 1 1 0 00 x5x4x2 2 –
00 0 1 1 0 0 0 00 x5x4x2 2 –
00 0 0 0 0 0 1 10 x5x4x2 2 –
01 0 0 0 0 0 0 00 x4x3x2 1 –
00 0 0 0 0 0 0 00 x4x3x2 0 = =1
3 0K
01 0 0 0 0 0 0 00 x5x3x2 1
00 0 0 0 0 0 0 00 x5x3x2 0 = =1
3 0K
00 0 0 0 0 0 0 00 x4x3x2 0 = =1
3 0K
00 0 0 0 0 0 0 01 x4x3x2 1
00 0 0 0 0 0 0 00 x5x3x2 0 = =1
3 0K
00 0 0 0 0 0 0 01 x5x3x2 1
01 0 0 0 0 0 0 00 x5x4x2 1
00 0 0 0 0 0 0 00 x5x4x2 0 = =1
3 0K
00 0 0 0 0 0 0 00 x5x4x2 0 = =1
3 0K
00 0 0 0 0 0 0 01 x5x4x2 1
11 0 0 0 0 0 0 00 x5x4x3 2
00 0 0 0 1 0 0 00 x5x4x3 1
00 0 1 0 0 0 0 00 x5x4x3 1
00 0 0 0 0 0 1 00 x5x4x3 1
00 1 0 0 0 0 0 00 x5x4x3 1
00 0 0 0 0 1 0 00 x5x4x3 1
00 0 0 1 0 0 0 00 x5x4x3 1
00 0 0 0 0 0 0 11 x5x4x3 2
7. %# BF =4,
= = =1
4 0K = ===0
4 2
16
32
16
2
K
n
( . . 3.10)

96. 96
' 3.10
0$-$ - -$ %&; 1 $-$ $5#&94 &--
5 # : ; -19 : 6 & =4
0$-&" % "1 &" 1
4%1 $ ! -
> 4%1$ $ !.
#.1 . 1
4%1 $ ! -
&1 -$--4
1 & 3
01 0 0 0 0 0 0 00 x4x3x2x1 1
01 0 0 0 0 0 0 00 x5x3x2x1 1
00 0 0 0 0 0 0 01 x4x3x2x1 1
00 0 0 0 0 0 0 01 x5x3x2x1 1
01 0 0 0 0 0 0 00 x5x4x2x1 1
00 0 0 0 0 0 0 01 x5x4x2x1 1
11 0 0 0 0 0 0 00 x5x4x3x1 2 = =0
4 2K
00 0 0 0 1 0 0 00 x5x4x3x1 1
00 0 1 0 0 0 0 00 x5x4x3x1 1
00 0 0 0 0 0 1 00 x5x4x3x1 1
00 1 0 0 0 0 0 00 x5x4x3x1 1
00 0 0 0 0 1 0 00 x5x4x3x1 1
00 0 0 1 0 0 0 00 x5x4x3x1 1
00 0 0 0 0 0 0 11 x5x4x3x1 2 = =0
4 2K
10 0 0 0 0 0 0 00 x5x4x3x2 1
00 0 0 0 1 0 0 00 x5x4x3x2 1
00 0 1 0 0 0 0 00 x5x4x3x2 1
00 0 0 0 0 0 1 00 x5x4x3x2 1
00 1 0 0 0 0 0 00 x5x4x3x2 1
00 0 0 0 0 1 0 00 x5x4x3x2 1
00 0 0 1 0 0 0 00 x5x4x3x2 1
00 0 0 0 0 0 0 10 x5x4x3x2 1
00 0 0 0 0 0 0 01 x5x4x3x2 1
8. = ’ 8 x5x4x3x1, x5x4x3x1,
= 0.
9. %# BF
=n=5, = = =1
5 0K = ===0
5 1
32
32
32
2
K
n
( . . 3.11). = ’ 8 x5x4x3x2x1, x5x4x3x2x1,
= 0

97. 97
' 3.11
0$-$ - -$ %&; 1 $-$ $5#&94 &--
5 # : ; -19 : 6 & =5
0$-&" % "1 &" 1
4%1 $ ! -
> 4%1$ $ !.
#.1 . 1
4%1 $ ! -
&1 -$--4
1 & 3
01 0 0 0 0 0 0 00 x5x4x3x2x1 1 = =0
5 1K
00 0 0 0 0 0 0 01 x5x4x3x2x1 1 = =0
5 1K
10.. , = . ( .
. 3.12). " 4 = ; ’ –
, –
= 01
= =iK
8 8. % , '
( ), . & –
; ' 3
(x1, x5x4x2, x5x3x2, x4x5x2, x4x3x2, x3x5x2, x3x4x2).
' 3.12
$- %#4 ; $--4 1 -9 ! 0 #. $
(-$' --4
1 ; 9 =- $ K
& " ) # 1 6 7-&8 0 #. $
01
1= =K
x1
K=1
610
1= =K
-
= =1
2 0K
-
K=2
= =0
4 8K
x2x1
= =1
3 0K
x4x3x2, x5x3x2, x4x3x2, x5x3x2, x5x4x2, x5x4x2
K=3
= =0
3 4K
-
= =1
4 0K
-
K=4
= =0
4 2K
x5x4x3x1, x5x4x3x1
= =1
5 0K
-
K=5
= =0
5 1K
x5x4x3x2x1, x5x4x3x2x1
11. 8 ,
: ’ . –

98. 98
BF = : .
– : ( . . 3.13).
' 3.13
$5#&94 %#4 & $--4 1 -9 ! 0 #. $
"1 &" 1 BF
0101 0111 0111 0111 0111 0111 0111 0101 )5(
1467447157f
"1 &" 1 6# 1$- > 6#.
0101 0101 0101 0101 0101 0101 0101 0101 x1
0000 0000 0011 0000 0000 0000 0011 0000 x4x3x2
0000 0000 0000 0000 0011 0000 0011 0000 x5x3x2
0000 0011 0000 0000 0000 0011 0000 0000 x4x3x2
0000 0011 0000 0011 0000 0000 0000 0000 x5x3x2
0000 0000 0000 0000 0011 0011 0000 0000 x5x4x2
0000 0000 0011 0011 0000 0000 0000 0000 x5x4x2
12.+ ; = :
12.1 ! . 3.13 – ,
BF = ( . . 3.14). .
– :
' 3.14
- # 0 $-$ $5#&94
%#4 & $--4 1 -9 ! 0 #. $
"1 &" 1 BF
11 111 111 111 111 111 111 11 f )5(
1467447157
.
-$ -&" 1 6# 1$- > 6#.
11 101 101 101 101 101 101 11 x1
00 000 011 000 000 000 011 00 x4x3x2
00 000 000 000 011 000 011 00 x5x3x2
00 011 000 000 000 011 000 00 x4x3x2
00 011 000 011 000 000 000 00 x5x3x2
00 000 000 000 011 011 000 00 x5x4x2
00 000 011 011 000 000 000 00 x5x4x2
11 123 123 123 123 123 123 11

99. 99
12.2$ ,
; . + ,
8 ,. + 8
, , = 1.
. 8 , . 8
BF ; :
y=x1∨…
12.3) 9 , ;
, ; ( . . 3.15),
; =8 , , 9 BF = ; =8 . .
– ,
, : 8 .
' 3.15
- # 0 $-$ $5#&94
%#4 & $--4 1 -9 ! 0 #. $
"1 &" 1 BF
1 1 1 1 1 1 y1467447157
.
"1 &"
1
6# 1$-
>
6#.
0 1 0 0 0 1 x4x3x2
0 0 0 1 0 1 x5x3x2
1 0 0 0 1 0 x4x3x2
1 0 1 0 0 0 x5x3x2
0 0 0 1 1 0 x5x4x2
0 1 1 0 0 0 x5x4x2
2 2 2 2 2 2
12.4+ =, 9 BF = .
& : ; , = :
y1=x1∨x5x3x2∨x4x3x2∨x5x4x2
y2=x1∨x5x4x2∨x4x3x2∨x5x4x2

100. 100
3.4 - 0$9 4 & 6 - 3 &0-$' -&8 5 # &8 ; -19 " %
6$ $# #.- : % 1 6 0&9 : 2#48 05 #.2 --4 0-$' --4 1 ; 9 =- $
" 8 (+&)
(SBF) &'4+ = 8 BF &'4+
BF, , 8
= S5 (3.1). ! 8 PO SBF = :
8 PO BF. . = ; . :
,
8 PO SBF [8, 12]:
1. " : BF ’
4
2. . 8 8
3. ’ , = BF, 8
4. $ ( )
BF, : = =
8 ; BF
= : 8. +
: :
1. ! : 8 : 8 : 8 8 8 PO BF
: 8 , ,
= 8 8 . ) ,
' ( : ),
BF . ! PO SBF =
8 : 8 BF, BF 8
; 8 = S5. +
= 8 S5
= 8 ,
= . : =
SL, SAD, SS ( . 1.1.2 1)

101. 101
2. , 9 ;
: 8 BF.
= ; , :
8 8 BF . # ;
, ;
BF , =
3. & = 8 PO SBF = ,
= S5 8
SBF, = S5
8 : 8 BF, 9 : . $
= 8 BF =
= 8 SBF , 9
= : = 8 BF, ,
8 BF, = 8
8 BF : ,
BF. % = ;
= :
==
≤=
mm
i
BF
i
mm
i
BFrez
i
SBF
SSS
11
ΣΣ , (3.1)
mm – BF SBF, iSΣ
BF
–
= 8 8 i- 8 BF,
BFrez
iSΣ – =
8 8 i- 8 BF,
( : ), 9
BF
+ 8 PO SBF : = , 9
PO BF &'4+ ;
.
+ =:

102. 102
• ; 8, BF,
; = , ;
= , . +
, : ;
• , 9 ,
; = 8 ; ( , ;
BF, 9 ) =
9 8 BF;
' . 3.2 / 8 PO SBF &'4+

103. 103
: : PO
BF , 9
9 = 8 ; ,
= ; 8 .
+ 8 PO SBF &'4+ = ( . . 3.2).
. = :
1. + ; BF .
= BF.
2. ! BF
: . ) 9 ;
: 8 – 8 BF
BF, ; – %# BF
3. &
: – : 8 BF. + : 8 BF ,
0 1
= =1.
4. ! – )1( =KiΦ BF,
1)1( ==KQi – :
5. + : 8 BF
= =2 ;
)2( =KiΦ :
6. + 8 = =3, 4,..., n
7. : 8 BF SBF 4 8
= S5
8. . BF 4 BF :
= S5 ; , 8
SBF
$ 8 PO SBF &'4+
.

104. 104
SBF, , = 5 BF, : 5
(n=5). BF SBF 146744715710,
92608991710, 313823787910, 99916955110, 301232578610.
BF 8 ( .
. 3.16) : .
' 3.16
$ BF, < 8 %4 . & ,
&!#4% 5 -$ - ! 1 $
#
; -19 :
> BF
10 )
-$ -&" 1 BF
$!$
5 -$ - !
1 $
)5(
1467447157y 1 467 447 157 0101 0111 0111 0111 0111 0111 0111 0101 22
)5(
926089917y 926 089 917 0011 0111 0011 0011 0000 0010 1011 1101 16
)5(
3138237879y 3 138 237 879 1011 1011 0000 1101 1011 0101 1011 0111 20
)5(
999169551y 999 169 551 0011 1011 1000 1110 0001 1110 0000 1111 17
)5(
301232786y 3 012 325 786 1011 0011 1000 1100 0111 0001 1001 1010 16
/ 8 PO BF 8 PO
BF ; : 8 BF " 4. . = :
1. $ %# BF f(5), 9
, %# 900
, . 3.4. 8
%# BF f(5) ;
, . 3.5.
:
2. 8 %# : 8 8 8 :
BF = =1
: ,
3.3 )1( =K
f
i
j
Φ , 1)1(
==K
f
i
j
Q ( )
0)1(
==K
f
i
j
Q ( )
3. ! : , 9 BF

105. 105
' 3.17
) # 1 6 7-&8 0 #. $ BF
) 4%1 &"
- 5 # :
; -19 :
#
; -19 :
6 & $#.-
0-$' --4
6 7-
0 #. $ BF
& " ) # 1 # - %6 %
=1 =
=
1
1
iQ
K x1
=2 =
=
0
2
iQ
K
x2x1
=3 =
=
1
3
iQ
K
x4x3x2[BF A2], x5x4x2, x5x3x2, x5x3x2[BF A3], x4x3x2,
x5x4x2
BF A1 )5(
1467447157y
=4 =
=
0
4
iQ
K x5x4x3x1, x5x4x3x1
=2 =
=
1
2
iQ
K x5x2
=
=
1
3
iQ
K x4x2x1, x4x3x2 [BF A1],
=3 =
=
0
3
iQ
K x4x2x1, x5x2x1, x3x2x1, x5x4x1, x4x3x2, x5x4x2, x5x4x2
=4 =
=
1
4
iQ
K
x5x4x3x2, x5x4x3x1, x4x3x2x1, x5x4x3x1, x5x4x3x1,
x5x4x2x1
BF A2 )5(
926089917y
=5 =
=
0
5
iQ
K x5x4x3x1
=
=
1
3
iQ
K
x5x3x1, x3x2x1, x5x3x1, x5x4x1, x4x2x1[BF A5], x4x3x1,
x5x2x1, x4x3x2, x5x3x2[BF A1], x5x4x2, x5x4x2, x4x3x1=3
=
=
0
3
iQ
K x3x2x1, x5x4x3
=
=
1
4
iQ
K x5x3x2x1, x5x4x3x1, x4x3x2x1, x5x4x3x2 [BF A5]
BF A3 )5(
3138237879y
=4 =
=
0
4
iQ
K x5x3x2x1, x5x4x2x1, x5x4x3x1, x5x4x2x1
=2 =
=
1
2
iQ
K x3x1
=
=
1
3
iQ
K x5x4x3, x5x3x2, x4x3x2, x5x4x2 [BF A5]
=3
& " 0 x5x3x1, x3x2x1, x4x3x1, x4x3x2, x5x3x2, x4x3x2, x5x4x3
=
=
1
4
iQ
K x4x3x2x1, x5x4x2x1
BF A4 )5(
999169551y
=4
& " 0 x5x4x2x1, x5x4x2x1
=
=
1
3
iQ
K x4x2x1 [BF A3], x4x2x1, x4x3x2 [BF A3], x5x4x2[BF A4]
=3
& " 0 x4x3x2, x5x4x2
=
=
1
4
iQ
K
x5x4x3x1, x5x3x2x1, x5x4x3x1, x5x4x3x2 [BF A3],
x5x4x3x1, x5x3x2x1, x4x3x2x1
BF A5 )5(
301232786y
=4
=
=
0
4
iQ
K
x5x4x2x1, x4x3x2x1, x5x4x3x1, x4x3x2x1, x5x3x2x1,
x5x3x2x1, x5x4x2x1, x5x4x2x1, x4x3x2x1, x5x4x3x1,
x5x4x3x1
4. + : 8 BF %# BF
= =2, ; =
, =1

106. 106
5. BF, 9 : , n=5,
=2,3,4,5 8. + =2
= ' , 9
2- , =3 – 3- , =4 – 4- ,
=5 – 5- .
6. % ; .3.1.2.1, ;
8 : ,
BF : . + 8
= " 4 BF,
: ( . . 3.17)
' 3.18
) # 1 0 #. $ BF - $#.- " +
) 4%1 &"
-
5 # :
; -19 :
#
; -19 : > 0 #. $ & BF - $#.- " +
1) y1=x1∨x5x3x2∨x4x3x2∨x5x4x2
BF A1 )5(
1467447157y
2) y2=x1∨x5x4x2∨x4x3x2∨x5x4x2
1) y1=x4x2x1∨x5x4x3x2∨x5x2∨x5x4x3x1∨x4x3x2x1∨x5x4x3x1
BF A2 )5(
926089917y
2) y2=x5x4x3x1∨x4x3x2∨x5x2∨x5x4x2x1∨x4x3x2x1∨x5x4x3x1
1) y1=x5x4x2∨x5x3x1∨x3x2x1∨x5x3x1∨x4x3x2∨x5x4x3x2∨x5x4x1
2) y2=x5x4x2∨x5x3x1∨x3x2x1∨x5x3x1∨x4x2x1∨x5x4x3x2∨x5x4x1
3) y3=x5x4x2∨x5x3x1∨x4x3x1∨x5x3x1∨x4x2x1∨x5x3x2x1∨x5x4x1
BF A3 )5(
3138237879y
4) y4= x5x4x2∨x5x3x1∨x4x3x1∨x5x3x1∨x4x2x1∨x5x4x3x2∨x5x4x1
BF A4 )5(
999169551y 1) y1=x5x4x3∨x3x1∨x5x3x2∨x4x3x2∨x4x3x2x1∨x5x4x2∨x5x4x2x1
1) y1=x5x4x3x1∨x5x3x2x1∨x4x2x1∨x4x2x1∨x4x3x2∨x5x4x3x1∨x5x4x3x2∨x5x4x2∨x5x4x3x1
BF A5 )5(
301232786y
2) y2=x5x4x3x1∨x5x3x2x1∨x4x2x1∨x4x2x1∨x4x3x2∨x5x4x3x1∨x5x4x3x2∨x5x4x2∨x5x3x2x1
7. : 8 BF SBF 4 (
8 BF). : BF : .
' = 4 : 8 BF SBF

107. 107
( . . 3.18). & , ;
" 4 BF : = BF. %
" 4 : 8 BF
.
8. .
4 BF, = 8
; SBF 8 4 BF:
' ’ 1
∨∨∨∨∨∨∨∨=
∨∨∨∨∨∨=
∨∨∨∨∨∨=
∨∨∨∨∨=
∨∨∨=
1345
_
2452
_
3
_
45
_
134
_
5
_
23412
_
4
_
1
_
24
_
1
_
23
_
51
_
3
_
4
_
55
12
_
45
_
245
_
1
_
2342
_
3
_
42
_
3
_
51
_
3
_
3
_
4
_
54
1452
_
3
_
45
_
23413
_
5
_
1
_
2
_
3
_
1
_
3
_
5
_
2
_
4
_
53
_
1
_
3451
_
2
_
3412
_
4
_
5
_
25
_
23
_
4
_
1
_
3
_
4
_
52
_
24
_
5
_
23
_
4
_
2
_
35
_
11
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxy
xxxxxxxxxxxxxxxxxxxxxxy
xxxxxxxxxxxxxxxxxxxxxxy
xxxxxxxxxxxxxxxxxxxxxy
xxxxxxxxxxy
' ’ 2
∨∨∨∨∨∨∨∨=
∨∨∨∨∨∨=
∨∨∨∨∨∨=
∨∨∨∨∨=
∨∨∨=
1235
_
2452
_
3
_
45
_
134
_
5
_
23412
_
4
_
1
_
24
_
1
_
23
_
51
_
3
_
4
_
55
12
_
45
_
245
_
1
_
2342
_
3
_
42
_
3
_
51
_
3
_
3
_
4
_
54
1452
_
3
_
45
_
23413
_
5
_
1
_
2
_
3
_
1
_
3
_
5
_
2
_
4
_
53
_
1
_
3451
_
2
_
3412
_
4
_
5
_
25
_
23
_
4
_
1
_
3
_
4
_
52
_
24
_
5
_
23
_
4
_
2
_
35
_
11
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxy
xxxxxxxxxxxxxxxxxxxxxxy
xxxxxxxxxxxxxxxxxxxxxxy
xxxxxxxxxxxxxxxxxxxxxy
xxxxxxxxxxy
3.5 - 0$9 4 '$ 1 &0-$' -&8 5 # &8 ; -19 " % 6$ $# #.- :
% 1 6 0&9 : 2#48 05 #.2 --4 0-$' --4 1 ; 9 =- $
/ =
, %# BF, %#
. ! : – 0 1. BF
(ChO BF) [7]
$ ( = ) ChO BF – ;
( ) %#

108. 108
%#. ) 9 BF f(x1,x2,x3,...,xn) m %# n ,
BF =:
%100
2
2
⋅
−
= n
n
m
k ,
) 9 k=100%, BF = (PO BF). :
BF, ; : PO BF = ChO BF. >
8 ChO BF : 2m
PO BF. ) ,
%# , :
; . ChO BF
, 9 88 = S5 ;
: .
" 8 ChO BF &'4+ =
8 BF &'4+ BF,
= S5
! 8 ChO BF &'4+ = : PO BF.
. = ; . :
, 8
ChO BF:
1. ! =8 : PO BF, = ChO BF, PO BF, 9
= S5. ;
ChO BF , 9
: = S5
2. 8 BF ;
4 8 = S5
3. . : ’ ; , =
= S5
, : ;
, = : 8. +
: :

109. 109
1. . = =
BF. : , ;
= ;
2. BF : 8,
BF 8 ,
. + 8 ChO BF
, 9 : 8
- " " "
.
' .3.3 / 8 ChO BF &'4+ ;

110. 110
+ 8 BF &'4+ = : =
; 8 ChO BF &'4+. +
8 ChO BF &'4+ = ,
. ! = PO BF (
BF) =8 : : 8 ChO BF, ;
8 ChO BF 4. ! ; , : 8
8 BF = 4 ( :
4). ! 8 : 4
: 8 PO BF
+ 8 (PO
BF) (&'4+) = ( . . 3.3).
. = :
1. 4 ; 8 8 BF n .
2. $ 8 ; 8 8
BF n . + ;
– ,
; . ; .
3. . ; iΦ , 1i =Q 0i =Q ,
= K=1..n ( . . 3.19)
' 3.19
& ", 6 & 41 1 ' = . 4 %6 %-$
-; $9 "-$ '$ &-$ 5 # : ; -19 :
- . %&-&9. 6'&1 $ ! - $
6 4 " 0$- " %&; 1 $- "
$5#&9 &-- 5 # : ; -19 :
- . %&-&9. 6'&1 $ ! - $
- - " 0$- " %&; 1 $- "
$5#&9 &-- 5 # : ; -19 :
-; $9 "-$
'$ &-$ % -3=
1
-; $9 "-$
'$ &-$ % -3=
0
-; $9 "-$
'$ &-$ % -3=
1
-; $9 "-$
'$ &-$ % -3=
0
jn
jK
Q
jK
−
=
=
= =+ 2*1i
( =
= >1i
0Q
jK , j=1..n)
=
= =0i
0Q
jK
( = >*
0jK , j=1..n)
=
= =0i
0Q
jK
( = >*
0jK , j=1..n)
jn
jK
Q
jK
−
=
=
= =+ 2*1i
( =
= >1i
0Q
jK , j=1..n)

111. 111
4. : = K
iΦ BF –
9 BF : iΦ
– = BF ; iΦ
= K+1, 9 = – = BF,
; = : .
5. + ChO BF 8
; 8 8 – ,
= 2
6. + iΦ K=1, 1i ≠Q 0i ≠Q , :
iΦ K=2, 3,…, n
7. + ; iΦ , 1i =Q 0i =Q ,
= K=n
8. ' 8 8 8 8 : =
, 9 = ; =
8, : BF, 9 ChO BF. +
8 iΦ ,
; 8
ChO BF
$ ChO BF .
ChO BF, = 5 (n=5) =
01**0****1****1*****0*1***1***012 ( «*»
%#, ).
BF = – 31,25%.
/ 8 = :
1. $ %# BF f(5), , %#
900
, . 3.20.
2. + %# BF f(5) ;
, . 3.20.

112. 112
.
: iΦ BF =1, =
8 iQ BF
' 3.20
%&; 1 $-$ $5#&94 &--
"1 &" 5 -$ -&" 1 4%1$ BF
01** 0*** *1** **1* **** 0*1* **1* **01 )5(
1467447157f
4%1& $ ! -
1010 1010 1010 1010 1010 1010 1010 1010 x1
0101 0101 0101 0101 0101 0101 0101 0101 x1
1100 1100 1100 1100 1100 1100 1100 1100 x2
0011 0011 0011 0011 0011 0011 0011 0011 x2
1111 0000 1111 0000 1111 0000 1111 0000 x3
0000 1111 0000 1111 0000 1111 0000 1111 x3
1111 1111 0000 0000 1111 1111 0000 0000 x4
0000 0000 1111 1111 0000 0000 1111 1111 x4
1111 1111 1111 1111 0000 0000 0000 0000 x5
0000 0000 0000 0000 1111 1111 1111 1111 x5
3. . 3.5 ; 8 BF
( BF) ( . . 3.20). . BF
8
8
4. . 4 6 . %
; ,
8 8, ;
, =
: – = «0»
= «*» BF. + ;
( = K=1),
= , 9 = , =:
=
= =1
1
i
0Q
K , 9 = =≠*
1 16
2
K
n
,

113. 113
=
=
1
1
iQ
K – 1i =Q – , 9
BF, =
*
1K – , 9
«*» BF = K=1,
= , 9 = , = ( .
. 3.19):
=
=
= ===+ *
1
0
1 16
2
32
2
2i
K
n
Q
K , 9 =
= >0
1
i
0Q
K
=
=
0
1
iQ
K – 0i =Q – , 9
BF, =
*
1K – , 9
«*» BF = K=1
5. . ( . . 3.21) = , 9 =
=1 ; 8 x1 1i =Q , x1 =
’ . % BF
«*» «1» – BF. +
, BF = , –
' 3.21
0$-$ - -$ %&; 1 $-$ $5#&94 &--
5 # : ; -19 : 6 & =1
0$-&" "1 &" 5 -$ -&" 1 4%1$ BF
0 * * 0 * * * * * * * * * * * * * 0 * * * * * * * 0
4%1& $ ! -
iΦ ΣΣΣΣ0000
ΣΣΣΣ∗∗∗∗
Σ0
+Σ∗
1 1 0 1 0 1 0 1 1 0 1 0 0 1 0 1 0 1 0 0 1 0 0 1 0 1 x1
4 9 13
0 0 1 0 1 0 1 0 0 1 0 1 1 0 1 0 1 0 1 1 0 1 1 0 1 0 x1 0 13 13
1 0 0 1 1 0 0 1 0 0 1 1 0 1 1 0 0 1 1 0 1 1 0 1 1 0 X2
3 11 14
0 1 1 0 0 1 1 0 1 1 0 0 1 0 0 1 1 0 0 1 0 0 1 0 0 1 x2
1 11 12
1 1 1 0 0 0 0 1 1 1 0 0 0 1 1 1 1 0 0 0 1 1 1 0 0 0 X3
1 12 13
0 0 0 1 1 1 1 0 0 0 1 1 1 0 0 0 0 1 1 1 0 0 0 1 1 1 x3
3 10 13
1 1 1 1 1 1 1 0 0 0 0 0 0 1 1 1 1 1 1 1 0 0 0 0 0 0 X4
3 11 14
0 0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 0 1 1 1 1 1 1 x4
1 11 12
1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 X5
2 11 13
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 x5
2 11 13
0$-&" % &0-$' -&" "1 &" 5 -$ -&" 1 4%1$ BF
0 * 1 0 1 * 1 * * 1 * 1 1 * 1 * 1 0 1 1 * 1 1 * 1 0 x1

114. 114
6.
8 8 =2 ( . . 3.22).
' 3.22
0$-$ - -$ %&; 1 $-$ $5#&94 &-- 5 # : ; -19 : 6 & =1
0$-&" "1 &" 5 -$ -&" 1 4%1$ BF
0 * 0 * * * * * * 0 * * 0
4%1& $ ! -
iΦ Σ0
Σ*
Σ0
+Σ*
1 0 1 0 1 0 1 1 0 1 1 1 0 x2x1 3 5 8
0 1 0 1 0 1 0 0 1 0 0 0 1 x2x1 1 4 5
1 1 0 0 1 1 0 1 1 0 1 0 0 x3x1 1 6 7
0 0 1 1 0 0 1 0 0 1 0 1 1 x3x1 3 3 6
1 1 1 1 0 0 0 1 1 1 0 0 0 x4x1 3 4 7
0 0 0 0 1 1 1 0 0 0 1 1 1 x4x1 1 5 6
1 1 1 1 1 1 1 0 0 0 0 0 0 x5x1 2 5 7
0 0 0 0 0 0 0 1 1 1 1 1 1 x5x1 2 4 6
1 0 0 0 1 0 0 1 0 0 1 0 0 x3x2 1 3 4
0 0 1 0 0 0 1 0 0 1 0 1 0 x3x2 2 2 4
1 0 1 0 0 0 0 1 0 1 0 0 0 x4x2 3 1 4
0 0 0 0 1 0 1 0 0 0 1 1 0 x4x2 0 4 4
1 0 1 0 1 0 1 0 0 0 0 0 0 x5x2 2 2 4
0 0 0 0 0 0 0 1 0 1 1 1 0 x5x2 1 3 4
0 1 0 0 0 1 0 0 1 0 0 0 0 x3x2 0 3 3
0 0 0 1 0 0 0 0 0 0 0 0 1 x3x2 1 1 2
0 1 0 1 0 0 0 0 1 0 0 0 0 x4x2 0 3 3
0 0 0 0 0 1 0 0 0 0 0 0 1 x4x2 1 1 2
0 1 0 1 0 1 0 0 0 0 0 0 0 x5x2 0 3 3
0 0 0 0 0 0 0 0 1 0 0 0 1 x5x2 1 1 2
1 1 0 0 0 0 0 1 1 0 0 0 0 x4x3 1 3 4
0 0 0 0 1 1 0 0 0 0 1 0 0 x4x3 0 3 3
1 1 0 0 1 1 0 0 0 0 0 0 0 x5x3 1 3 4
0 0 0 0 0 0 0 1 1 0 1 0 0 x5x3 0 3 3
0 0 1 1 0 0 0 0 0 1 0 0 0 x4x3 2 1 3
0 0 0 0 0 0 1 0 0 0 0 1 1 x4x3 1 2 3
0 0 1 1 0 0 1 0 0 0 0 0 0 x5x3 1 2 3
0 0 0 0 0 0 0 0 0 1 0 1 1 x5x3 2 1 3
1 1 1 1 0 0 0 0 0 0 0 0 0 x5x4 2 2 4
0 0 0 0 0 0 0 1 1 1 0 0 0 x5x4 1 2 3
0 0 0 0 1 1 1 0 0 0 0 0 0 x5x4 0 3 3
0 0 0 0 0 0 0 0 0 0 1 1 1 x5x4 1 2 3
0$-&" % &0-$' -&" "1 &" 5 -$ -&" 1 4%1$ BF
0 1 0 1 0 1 0 0 1 0 0 0 0
0 1 0 1 1 1 1 1 1 0 1 1 0
' = 8 ' , 9 2 =
, , 9 =1

115. 115
, 9 . 8 BF
’ 8, x1. 8
8 8 8 8 =2
8. = 1i =Q = =
= =1
2
i
0Q
K , 9
= =≠*
2 8
4
K
n
, = 0i =Q = ( . 3.3) =
=
= ===+ *
2
1
2 8
4
32
4
2i
K
n
Q
K
, 9 =
= >1
2
i
0Q
K . . =
, 9 , ,
: ,
BF.
7. % ; iΦ
= =3..5 : , 8
8 PO BF. :
8 BF ( . . 3.23), =
:
' 3.23
) # 1 6 7-&8 0 #. $ BF
) 4%1 &"
-
5 # :
; -19 :
#
; -19 :
6 & $#.-
0-$' --4
6 7-
0 #. $ BF
& " ) # 1 # - %6 %
=1 =
=
1
1
iQ
K x1
BF A1 )5(
2013263869y
=2 =
=
1
2
iQ
K x4x2, x4x2, x5x3, x5x2, x5x4
=1 =
=
1
1
iQ
K x1
BF A2 )5(
2004318069y
=2 =
=
1
2
iQ
K x3x2, x4x2, x5x2
8. % , 8 =8 : ChO BF
PO BF )5(
2013263869y )5(
2004318069y , .
=
. .
8 BF = , 9 ChO BF

116. 116
= , = ;
. % = : 8 PO BF )5(
2013263869y )5(
2004318069y .
. = 8 ChO BF:
BF )5(
2013263869y :
y1=x1∨x5x3∨x4x2∨x5x2
y2=x1∨x5x3∨x4x2∨x5x4
BF )5(
2004318069y :
y=x1∨x3x2∨x4x2∨x5x2
3.6 - 0$9 4 & '$ 1 &0-$' -&8 5 # &8 ; -19 " %
6$ $# #.- : % 1 6 0&9 : 2#48 05 #.2 --4 0-$' --4 1 ; 9 =- $
! 8 ChO SBF = :
; 8 BF :
BF, :
; , ’ ; =
8. ! 8 ChO SBF : ,
: 8 ChO SBF
[12]:
1. : ChO BF , 9
; " 4 =8 : BF, =
ChO BF
2. : 8 8 ChO BF
' 4 8 8
3. ; BF 8
4. $ ( )
BF, : 8 4, : =
; BF
= : 8. +
: :

117. 117
1. ! : 8 : 8 : 8 8
8 ChO BF : ; 8
= 8 8 . ) ,
' ( : ),
BF . ! ChO SBF =
%# : 8 BF, BF
8 ; 8
= S5. + = 8 S5
= 8
, = .
: = :
• Sl. – BF. &'4+ =
=
=
=
m
i
KS iL
1
;
• SAD – BF. &'4+ =
= mSAD = ;
• SS – 9 07. &'4+ = =
mnSAD ⋅⋅= 2
n – , m –
BF, i – i- BF
2. , 9 ;
: 8 BF.
= ; , :
8 8 BF . # ;
, ;
BF , =
3. & = 8 ChO SBF = ,
= S5 8

118. 118
SBF, = S5
8 : 8 BF, 9 : .
$ = 8 BF =
= 8 SBF , 9
= : =
8 BF, , 8 BF,
= 8 8 BF
: , BF. %
= ; = :
=
Σ
=
Σ ≤=
mm
i
BFU
i
mm
i
BFU
i
SBFU
SSS
11
, (6)
mm – BF SBF, iSΣ
BFU
– =
8 i- BF,
BFU
iSΣ –
= 8 i- BF
( : ), BF
" ; ,
BF ; ,
, ; = , :
8 ChO SBF. 8 =
: 8 ChO SBF:
• 8 PO BF &'4+ ;
, = :
: ChO BF , ,
BF , 9 9 = ;
= ; ;
• , 9 ,
; = 8 ; BF = 9
BF

119. 119
3.7 - 0$9 4 6 - 3 &0-$' -&8 5 # &8 ; -19 " % 6$ $# #.- :
% 1 6 0&9 : 2#48 0 -2 --4 0-$' --4 1 ; 9 =- $
) : ; , '= 8 8 =
BF. + : :
1.> ; = 0 n [6].
iQ .
8 8 ; TI BF =
iΦ optKK =
2.> ; = n 0 [16].
iΦ .
8 8 ; TI BF =
iΦ optKK = ;
« ; »
& ; = 8
. . ; . !
; = ; ; , = :
8 8 ,
8 8 ;
, :
: 9 8
.
> 8 ; ; = =
. ! = = ; . . =
: BF (PO)
8 (ChO) BF ; 8 8
.
. 8 ; 8 = ; . /
8 PO BF ),...,,,( 321 nxxxxfy = 8 8 ;

120. 120
; = = ( .
. 3.4):
' . 3.4 / 8 PO BF &'4+ ; iQ
& 8 = TI PO BF ),...,,,( 321 nxxxxfy = . 8
TI BF (UTI PO BF) ),...,,,( 321 nxxxxfy = , ;
TI BF , = ,

121. 121
2. + : UTI BF. &
(VES STROKI)
3. . UTI BF n
SUTIBF 0_ , n
SUTIBF 1_ , n
SUTIBF 2_ ,
…, n
nSUTIBF 1_ − , n
nSUTIBF _ 0
n. + « ; »
iQ = = 8
iΦ . 7 iΦ = = , 9 8
( , :
) ,
= . $ « ; »
. . = : ,
n
iSUTIBF _ n
iSUTIBF 1_ +
4. + ; : n
iSUTIBF _
n
iSUTIBF 1_ + (i=0..n-1), = ,
n
iiSUTIBF 1,_ + (i=0..n-1)
= , ; « ; »
«*»
5. + n
iiSUTIBF 1,_ + (i=0..n-1)
, 8 ( *
1,1, __ n
ii
n
ii SUTIBFSUTIBF ++ → )
6. ! 1
_ +n
iSUTIBF (i=0..n) nREZ Φ_ ,
« ; »
7. 8 4, 5, 6 { *
1,0_ n
SUTIBF , *
2,1_ n
SUTIBF , …, *
1,2_ n
nnSUTIBF −− ,
*
,1_ n
nnSUTIBF − } { *
2,1,0_ n
SUTIBF , *
3,2,1_ n
SUTIBF , …, *
1,2,3_ n
nnnSUTIBF −−− ,
*
,1,2_ n
nnnSUTIBF −− } : 1_ −nREZ Φ
8. 8 4, 5, 6 , *...
..._ SUTIBF
jREZ Φ_ (j=n..0). .
(

122. 122
= =i : . .
( , optKK =
3.8 - 0$9 4 '$ 1 &0-$' -&8 5 # &8 ; -19 " % 6$ $# #.- :
% 1 6 0&9 : 2#48 0 -2 --4 0-$' --4 1 ; 9 =- $
> 8 #hO BF ),...,,,( 321 nxxxxfy = 8 8
; ; =
8 PO BF = ( . . 3.5):
' . 3.5 / 8 PO BF &'4+
;

123. 123
1. & 8 = TI #hO BF ),...,,,( 321 nxxxxfy = . .
: :
o «1» - « »,
o «0» - « »,
o «*» - « ».
8 TI BF (UTI #hO BF) ),...,,,( 321 nxxxxfy = ,
; TI BF , =
2. + : UTI BF. &
(VES STROKI)
3. . UTI BF n
SUTIBF 0_ , n
SUTIBF 1_ , n
SUTIBF 2_ ,
…, n
nSUTIBF 1_ − , n
nSUTIBF _ 0
n
+ « ; »
iQ = = 8
iΦ . 7 iΦ = = , 9 8 (
, :
) , =
. $ « ; »
. +
«1», 9 = «1»,
; «*». . = : ,
n
iSUTIBF _ n
iSUTIBF 1_ +
4. + ; : n
iSUTIBF _
n
iSUTIBF 1_ + (i=0..n-1), = ,
n
iiSUTIBF 1,_ + (i=0..n-1)
= , ; « ; »
«*»

124. 124
5. + n
iiSUTIBF 1,_ + (i=0..n-1)
, 8 ( *
1,1, __ n
ii
n
ii SUTIBFSUTIBF ++ → )
6. ! 1
_ +n
iSUTIBF (i=0..n) nREZ Φ_ ,
« ; »
7. 8 4, 5, 6 { *
1,0_ n
SUTIBF , *
2,1_ n
SUTIBF , …, *
1,2_ n
nnSUTIBF −− ,
*
,1_ n
nnSUTIBF − } { *
2,1,0_ n
SUTIBF , *
3,2,1_ n
SUTIBF , …, *
1,2,3_ n
nnnSUTIBF −−− ,
*
,1,2_ n
nnnSUTIBF −− } : 1_ −nREZ Φ
8. 8 4, 5, 6 , *...
..._ SUTIBF
jREZ Φ_ (j=n..0). .
(
= =i : . .
( , optKK =
9. . jREZ Φ_ (j=n..0) ,
«*». .
( , optKK =
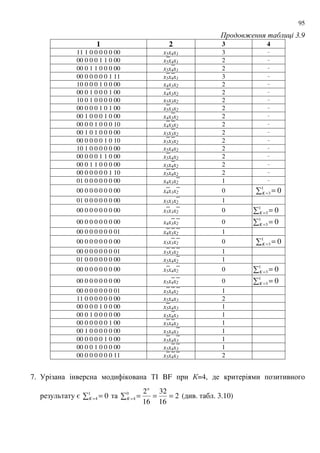
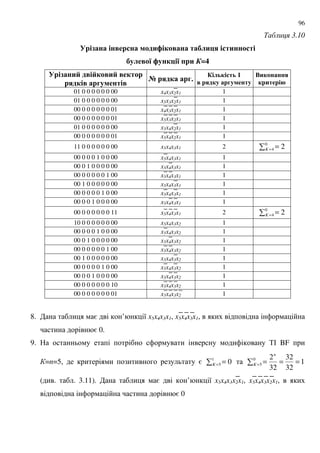
3.9 - 0$9 4 5 # &8 ; -19 " $ &'-& % 6$ $# #.- :
% 1 6 0&9 :
" BF (PO BF) &'4+ ; ;
= 0 n [6] ; ; =
n 0 [16] = 8.
& ; . : ; =
.
" BF ; ; = 0 n
= ; TI BF. + 8 =:
1. . ; %# BF, 9 = :
= ;

125. 125
2. . ; %# BF, 9 = :
8 ;
; %#
3. & 8
:
4. " : 8 ,
8 , 9 = : = 9
8 +
5. / = : = :
: 8 , 9 = :
8
6. = 8 BF
8 BF ; ; =
0 n, 9 = 8, =:
1. ! : iΦ
= , 9 : 8 .
$ : , 9 =
: iΦ = ,
8 , 9 ; iΦ , . % BF
8
= nK ≅ : iΦ = , 9
= = 8
" BF ; ; = 0 n
= ; . + 8 =:
1. & ; %# BF, 9 ,
= : = 8
2. & %# BF = =
« ; » iQ
3. = 8 BF

126. 126
8 BF ; ; =
0 n, 9 = 8, =:
1. & ; , 9
8 8
' 3.24
$5#&94 &-- BF )5(
1467447157f
4%1& $ ! -
5x 4x 3x 2x 1x
)5(
1467447157f
0 #. $ & -
4%1& BF
1 2 3 4 5 6 7
0 0 0 0 0 1 00000
0 0 0 0 1 0
0 0 0 1 0 1 00010
0 0 0 1 1 0
0 0 1 0 0 1 00100
0 0 1 0 1 1 00101
0 0 1 1 0 1 00110
0 0 1 1 1 0
0 1 0 0 0 1 01000
0 1 0 0 1 1 01001
0 1 0 1 0 1 01010
0 1 0 1 1 0
0 1 1 0 0 1 01100
0 1 1 0 1 1 01101
0 1 1 1 0 1 01110
1 2 3 4 5 6 7
0 1 1 1 1 0
1 0 0 0 0 1 10000
1 0 0 0 1 1 10001
1 0 0 1 0 1 10010
1 0 0 1 1 0
1 0 1 0 0 1 10100
1 0 1 0 1 1 10101
1 0 1 1 0 1 10110
1 0 1 1 1 0
1 1 0 0 0 1 11000
1 1 0 0 1 1 11001
1 1 0 1 0 1 11010
1 1 0 1 1 0
1 1 1 0 0 1 11100
1 1 1 0 1 0
1 1 1 1 0 1 11110
1 1 1 1 1 0
2. & : ,
8

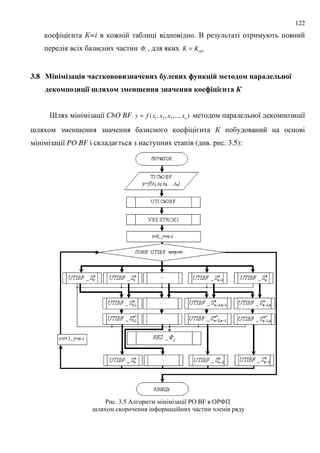
127. 127
3. : . +
8
; =
8 8 [17]. =
%# BF 8. "
8 8 = 8 BF, 9
.
8 PO BF &'4+ ;
= ( . . 3.6).
$ 8 .
BF, , , = 1 467 447 18710 (
0101 0111 0111 0111 0111 0111 0111 01012), = 5 (n=5).
/ 8 = :
13.. %# BF )5(
1467447157f ( . . 3.24),
= – %# BF
14.. – {00000, 00100,
00100, 00101, 00110, 01000, 01001, 01010, 01100, 01101, 01110, 10000, 10001,
10010, 10100, 10101, 10110, 11000, 11001, 11010, 11100, 11110}
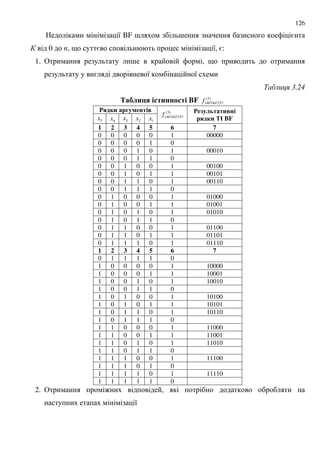
' 3.25
$ ! - BF f(5) %#4 - 0$9 : BF +)
1 ' --4 -; $9 "-&8 '$ &- '# - 4%
"1 &" 1 % 4%1 $ ! - > $ !.
($6& $ ! - &!#4%
- ! 4%1 BF
1010 1010 1010 1010 1010 1010 1010 1010 1x ****1
1100 1100 1100 1100 1100 1100 1100 1100 2x ***1*
1111 0000 1111 0000 1111 0000 1111 0000 3x **1**
1111 1111 0000 0000 1111 1111 0000 0000 4x *1***
1111 1111 1111 1111 0000 0000 0000 0000 5x 1****
15.$ %# BF f(5),
: , %# 900
, . 3.25, 9
%# :

128. 128
16.+ %# BF ;
, . 3.26
. = BF =1
' 3.26
%&; 1 $-$ %#4 - 0$9 : BF +)
1 ' --4 -; $9 "-&8 '$ &- '# - 4%
"1 &" 1 4%1 $ ! -
> $ !.
BF
($6& $ ! -
&!#4% . 4%1 BF
1010 1010 1010 1010 1010 1010 1010 1010 1x ****1
0101 0101 0101 0101 0101 0101 0101 0101 1x ****0
1100 1100 1100 1100 1100 1100 1100 1100 2x ***1*
0011 0011 0011 0011 0011 0011 0011 0011 2x ***0*
1111 0000 1111 0000 1111 0000 1111 0000 3x **1**
0000 1111 0000 1111 0000 1111 0000 1111 3x **0**
1111 1111 0000 0000 1111 1111 0000 0000 4x *1***
0000 0000 1111 1111 0000 0000 1111 1111 4x *0***
1111 1111 1111 1111 0000 0000 0000 0000 5x 1****
0000 0000 0000 0000 1111 1111 1111 1111 5x 0****
17. . 3.26 ; BF – BF 2 +$ (
BF) ( . . 3.27)
' 3.27
%&; 1 $-$ 02& -$ $5#&94 &-- BF
6 & =1
"1 &" 1 4%1$ BF
0101 0111 0111 0111 0111 0111 0111 0101 )5(
1467447157f
"1 &" 1 4%1 $ ! -
1010 1010 1010 1010 1010 1010 1010 1010 1x ****1
0101 0101 0101 0101 0101 0101 0101 0101 1x ****0
1100 1100 1100 1100 1100 1100 1100 1100 2x ***1*
0011 0011 0011 0011 0011 0011 0011 0011 2x ***0*
1111 0000 1111 0000 1111 0000 1111 0000 3x **1**
0000 1111 0000 1111 0000 1111 0000 1111 3x **0**
1111 1111 0000 0000 1111 1111 0000 0000 4x *1***
0000 0000 1111 1111 0000 0000 1111 1111 4x *0***
1111 1111 1111 1111 0000 0000 0000 0000 5x 1****
0000 0000 0000 0000 1111 1111 1111 1111 5x 0****

129. 129
18.+ , %# BF : :
. ! «*» = «0» «1». ) 9
: : – ( . . 3.28).
' 3.28
) 1$ -$# 7- -&8 4%1
$5#&9 0 #. $ & -&8 4%1
-&" 4% 1 BF
6 & =1
# - %6 %-
$5#&9
0 #. $ & -&8 4%1
0 #. $
1x ****1 00101 +
1x ****0 00000 +
2x ***1* 00110 +
2x ***0* 00000 +
3x **1** 00100 +
3x **0** 00000 +
4x *1*** 01000 +
4x *0*** 00000 +
5x 1**** 10000 +
5x 0**** 00000 +
& : , : %# BF =1 :
; BF
19.+ , ; BF )5(
1467447157f . .
10 22 . %
; , 8
8, ; ,
= ;
. + ; (
= K=1), = , 9
= – = =
= =1
1 0iQ
K , = , 9
= – = ( . . 3.3):
=
= ===0
1 16
2
32
2
2iQ
K
n

130. 130
' 3.29
0$-$ - -$ 02& -$ %&; 1 $-$ $5#&94 &--
5 # : ; -19 : 6 & =1
0$-&" % "1 &" 1 4%1$ BF
00 0 0 0 0 0 0 00 )5(
1467447157f
0$-&" % "1 &" 1 4%1 $ ! -
#.1 . 1
4%1
$ ! -
&1 -$--4
1 & 3
) !- 0
1 & 3
11 1 1 1 1 1 1 11 1x 10 - 8
0
2
?
≥=K
00 0 0 0 0 0 0 00 1x 0 = =1
1 0K -
10 1 1 1 1 1 1 10 2x 8 - 8
0
2
?
≥=K
01 0 0 0 0 0 0 01 2x 2 - 8
1
2
?
≤=K
11 0 1 0 1 0 1 00 3x 5 - 8
1
2
?
≤=K
00 1 0 1 0 1 0 11 3x 5 - 8
1
2
?
≤=K
11 1 0 0 1 1 0 00 4x 5 - 8
1
2
?
≤=K
00 0 1 1 0 0 1 11 4x 5 - 8
1
2
?
≤=K
11 1 1 1 0 0 0 00 5x 5 - 8
1
2
?
≤=K
00 0 0 0 1 1 1 11 5x 5 - 8
1
2
?
≤=K
. = , 9 1x = =1 ( . .
3.29) = ’ BF )5(
1467447157f ,
= .
20.. ,
1x (****0). . =
{00101, 01001, 01101, 10001, 10101, 11001}. # 22 ;
; 6
21. ( ; 8 8
=1), ,
. = ;
; 8 8
=2, 3,…, n. { 1x (****1), 2x
(***1*), 2x (***0*), 3x (**1**), 3x (**0**), 4x (*1***), 4x (*0***), 5x (1****), 5x (0****)}

131. 131
22. 8
8 8 8 8 =2.
= 8 ' , 9 2 , 9 8
. 8
= :
= ,
, 8 , , 9 8
. 8 BF )5(
1467447157f
’ 8, x1.
23.+ , %# BF =2 : :
, 9 : :
( . . 3.30). & : , 7
%# BF =2, 9 : ;
BF
' 3.30
) 1$ -$# 7- -&8 4%1
$5#&9 0 #. $ & -&8 4%1 6 & =2
-&" 4% 1 BF
# - %6 %- $5#&9
0 #. $ & -&8 4%1
0 #. $
1 2 3
12 xx ***11 - -
12 xx ***01 00101 +
13xx **1*1 00101 +
13xx **0*1 01001 +
14 xx *1**1 01001 +
14xx *0**1 00101 +
15xx 1***1 10001 +
x5x1 0***1 01001 +
x3x2 **11* - -
x3x2 **01* - -
x4x2 *1*1* - -
x4x2 *0*1* - -
x5x2 1**1* - -
x5x2 0**1* - -
x3x2 **10* 00101 +

132. 132
% 3.30
1 2 3
x3x2 **00* 01001 +
x4x2 *1*0* 01001 +
x4x2 *0*0* 00101 +
x5x2 1**0* 10001 +
x5x2 0**0* 00101 +
x4x3 *11** 01101 +
x4x3 *01** 00101 +
x5x3 1*1** 10101 +
x5x3 0*1** 00101 +
x4x3 *10** 01001 +
x4x3 *00** 10001 +
x5x3 1*0** 10001 +
x5x3 0*0** 01001 +
x5x4 11*** 11001 +
x5x4 01*** 01001 +
x5x4 10*** 10001 +
x5x4 00*** 00101 +
24. 8 8 8 8 8 =2
8. = = =1
2 0K
=
====
0
2
5
8
4
32
4
2
2
2
K K
n
( . . 3.31).
' 3.31
0$-$ - -$ %&; 1 $-$ $5#&94 &--
5 # : ; -19 : 6 & =2
0$-&" % "1 &" 1
4%1 $ ! -
> 4%1$
$ !.
#.1 . 1
4%1
$ ! -
&1 -$--4
1 & 3
1 2 3 4
01 0 0 0 0 0 0 01 x2x1 2 -
11 0 1 0 1 0 1 00 x3x1 5 -
00 1 0 1 0 1 0 11 x3x1 5 -
11 1 0 0 1 1 0 00 x4x1 5 -
00 0 1 1 0 0 1 11 x4x1 5 -
11 1 1 1 0 0 0 00 x5x1 5 -
00 0 0 0 1 1 1 11 x5x1 5 -
01 0 0 0 0 0 0 00 x3x2 1 -
00 0 0 0 0 0 0 01 x3x2 1 -
01 0 0 0 0 0 0 00 x4x2 1 -
00 0 0 0 0 0 0 01 x4x2 1 -
01 0 0 0 0 0 0 00 x5x2 1 -

133. 133
% 3.31
1 2 3 4
00 0 0 0 0 0 0 01 x5x2 1 -
11 0 0 0 1 0 0 00 x4x3 3 -
00 0 1 0 0 0 1 00 x4x3 2 -
11 0 1 0 0 0 0 00 x5x3 3 -
00 0 0 0 1 0 1 00 x5x3 2 -
00 1 0 0 0 1 0 00 x4x3 2 -
00 0 0 1 0 0 0 11 x4x3 3 -
00 1 0 1 0 0 0 00 x5x3 2 -
00 0 0 0 0 1 0 11 x5x3 3 -
11 1 0 0 0 0 0 00 x5x4 3 -
00 0 0 0 1 1 0 00 x5x4 2 -
00 0 1 1 0 0 0 00 x5x4 2 -
00 0 0 0 0 0 1 11 x5x4 3 -
25. % =3,
; = {00101, 01001, 01101, 10001, 10101, 11001}.
26.$ 8 8 8
8 8 =3 , %# BF
=3 : :
, 9 : : ( . . 3.32).
27.& : , 7 %# BF
=2, 9 : ; BF
' 3.32
) 1$ -$# 7- -&8 4%1
$5#&9 0 #. $ & -&8 4%1 6 & =3
-&" 4% 1 BF
# - %6 %- $5#&9
0 #. $ & -&8 4%1
0 #. $
1 2 3
x3x2x1 **101 00101 +
x3x2x1 **001 01001 +
x4x2x1 *1*01 01001 +
x4x2x1 *0*01 00101 +
x5x2x1 1**01 10001 +
x5x2x1 0**01 00101 +
x4x3x1 *11*1 01101 +
x4x3x1 *01*1 00101 +
x5x3x1 1*1*1 10101 +

134. 134
% 3.32
1 2 3
x5x3x1 0*1*1 00101 +
x4x3x1 *10*1 01001 +
x4x3x1 *00*1 10001 +
x5x3x1 1*0*1 10001 +
x5x3x1 0*0*1 01001 +
x5x4x1 11**1 11001 +
x5x4x1 01**1 01001 +
x5x4x1 10**1 10001 +
x5x4x1 00**1 00101 +
x4x3x2 *110* 01101 +
x4x3x2 *010* 00101 +
x5x3x2 1*10* 10101 +
x5x3x2 0*10* 00101 +
x4x3x2 *100* 01001 +
x4x3x2 *000* 10001 +
x5x3x2 1*00* 10001 +
x5x3x2 0*00* 01001 +
x5x4x2 11*0* 11001 +
x5x4x2 01*0* 01001 +
x5x4x2 10*0* 10001 +
x5x4x2 00*0* 00101 +
x5x4x3 011** 01101 +
x5x4x3 101** 10101 +
x5x4x3 001** 00101 +
x5x4x3 110** 11001 +
x5x4x3 010** 01001 +
x5x4x3 100** 10001 +
28.$ ; %# BF
=3, = = =1
3 0K = ===0
3 4
8
32
8
2
K
n
( .
. 3.33). . ’ x4x3x2 , x5x3x2, x4x3x2, x5x3x2,
x5x4x2, x5x4x2 = 8

135. 135
' 3.33
0$-$ - -$ %&; 1 $-$ $5#&94 &-- 5 # : ; -19 : 6 & =3
0$-&" % "1 &" 1
4%1 $ ! -
> 4%1$ $ !.
#.1 . 1
4%1 $ ! -
&1 -$--4
1 & 3
1 2 3 4
01 0 0 0 0 0 0 00 x3x2x1 1 –
00 0 0 0 0 0 0 01 x3x2x1 1 –
01 0 0 0 0 0 0 00 x4x2x1 1 –
00 0 0 0 0 0 0 01 x4x2x1 1 –
01 0 0 0 0 0 0 00 x5x2x1 1 –
00 0 0 0 0 0 0 01 x5x2x1 1 –
11 0 0 0 1 0 0 00 x4x3x1 3 –
00 0 1 0 0 0 1 00 x4x3x1 2 –
11 0 1 0 0 0 0 00 x5x3x1 3 –
00 0 0 0 1 0 1 00 x5x3x1 2 –
00 1 0 0 0 1 0 00 x4x3x1 2 –
00 0 0 1 0 0 0 11 x4x3x1 3 –
00 1 0 1 0 0 0 00 x5x3x1 2 –
00 0 0 0 0 1 0 11 x5x3x1 3 –
11 1 0 0 0 0 0 00 x5x4x1 3 –
00 0 0 0 1 1 0 00 x5x4x1 2 –
00 0 1 1 0 0 0 00 x5x4x1 2 –
00 0 0 0 0 0 1 11 x5x4x1 3 –
10 0 0 0 1 0 0 00 x4x3x2 2 –
00 0 1 0 0 0 1 00 x4x3x2 2 –
10 0 1 0 0 0 0 00 x5x3x2 2 –
00 0 0 0 1 0 1 00 x5x3x2 2 –
00 1 0 0 0 1 0 00 x4x3x2 2 –
00 0 0 1 0 0 0 10 x4x3x2 2 –
00 1 0 1 0 0 0 00 x5x3x2 2 –
00 0 0 0 0 1 0 10 x5x3x2 2 –
10 1 0 0 0 0 0 00 x5x4x2 2 –
00 0 0 0 1 1 0 00 x5x4x2 2 –
00 0 1 1 0 0 0 00 x5x4x2 2 –
00 0 0 0 0 0 1 10 x5x4x2 2 –
01 0 0 0 0 0 0 00 x4x3x2 1 –
00 0 0 0 0 0 0 00 x4x3x2 0 = =1
3 0K
01 0 0 0 0 0 0 00 x5x3x2 1
00 0 0 0 0 0 0 00 x5x3x2 0 = =1
3 0K
00 0 0 0 0 0 0 00 x4x3x2 0 = =1
3 0K
00 0 0 0 0 0 0 01 x4x3x2 1
00 0 0 0 0 0 0 00 x5x3x2 0 = =1
3 0K
00 0 0 0 0 0 0 01 x5x3x2 1
01 0 0 0 0 0 0 00 x5x4x2 1

136. 136
% 3.32
1 2 3 4
00 0 0 0 0 0 0 00 x5x4x2 0 = =1
3 0K
00 0 0 0 0 0 0 00 x5x4x2 0 = =1
3 0K
00 0 0 0 0 0 0 01 x5x4x2 1
11 0 0 0 0 0 0 00 x5x4x3 2
00 0 0 0 1 0 0 00 x5x4x3 1
00 0 1 0 0 0 0 00 x5x4x3 1
00 0 0 0 0 0 1 00 x5x4x3 1
00 1 0 0 0 0 0 00 x5x4x3 1
00 0 0 0 0 1 0 00 x5x4x3 1
00 0 0 1 0 0 0 00 x5x4x3 1
00 0 0 0 0 0 0 11 x5x4x3 2
29.. 8 =3,
. ) , –
. & 8 . ;
=4 =5 = ( . . 3.34)
' 3.34
$- %#4 ; $--4
1 -9 ! 0 #. $
(-$' --4
1 ; 9 =- $ K
& " ) # 1 6 7-&8 0 #. $
K=1 01
1= =K
x1
K=2 = =1
2 0K
-
K=3 = =1
3 0K
x4x3x2, x5x3x2, x4x3x2, x5x3x2, x5x4x2, x5x4x2
K=4 = =1
4 0K
-
K=5 = =1
5 0K
-
30. 8 ,
: ’ . –
BF = : .
– : ( . . 3.35).

137. 137
' 3.35
$5#&94 %#4 & $--4 1 -9 ! 0 #. $
"1 &" 1 BF
0101 0111 0111 0111 0111 0111 0111 0101 )5(
1467447157f
"1 &" 1 6# 1$- > 6#.
0101 0101 0101 0101 0101 0101 0101 0101 x1
0000 0000 0011 0000 0000 0000 0011 0000 x4x3x2
0000 0000 0000 0000 0011 0000 0011 0000 x5x3x2
0000 0011 0000 0000 0000 0011 0000 0000 x4x3x2
0000 0011 0000 0011 0000 0000 0000 0000 x5x3x2
0000 0000 0000 0000 0011 0011 0000 0000 x5x4x2
0000 0000 0011 0011 0000 0000 0000 0000 x5x4x2
31.+ ; = :
12.5 ! . 3.35 – ,
BF = ( . . 3.36). .
– :
' 3.36
- # 0 $-$ $5#&94
%#4 & $--4 1 -9 ! 0 #. $
"1 &" 1 BF
11 111 111 111 111 111 111 11 f )5(
1467447157
.
-$ -&" 1 6# 1$- > 6#.
11 101 101 101 101 101 101 11 x1
00 000 011 000 000 000 011 00 x4x3x2
00 000 000 000 011 000 011 00 x5x3x2
00 011 000 000 000 011 000 00 x4x3x2
00 011 000 011 000 000 000 00 x5x3x2
00 000 000 000 011 011 000 00 x5x4x2
00 000 011 011 000 000 000 00 x5x4x2
11 123 123 123 123 123 123 11
12.6$ ,
; . + ,
8 ,. + 8

138. 138
, , = 1.
. 8 , . 8
BF ; :
y=x1∨…
12.7) 9 , ;
, ; ( . . 3.37),
; =8 , , 9 BF = ; =8 . .
– ,
, : 8 .
' 3.37
- # 0 $-$ $5#&94
%#4 & $--4 1 -9 ! 0 #. $
"1 &" 1 BF
1 1 1 1 1 1 y1467447157
.
"1 &" 1 6# 1$- > 6#.
0 1 0 0 0 1 x4x3x2
0 0 0 1 0 1 x5x3x2
1 0 0 0 1 0 x4x3x2
1 0 1 0 0 0 x5x3x2
0 0 0 1 1 0 x5x4x2
0 1 1 0 0 0 x5x4x2
2 2 2 2 2 2
12.8+ =, 9 BF = .
& : ; , = :
y1=x1∨x5x3x2∨x4x3x2∨x5x4x2
y2=x1∨x5x4x2∨x4x3x2∨x5x4x2
3.10 - 0$9 4 BF +) 0 1 ' --4 $5 %&; 1$9 =3 -; $9 "-&8
'$ &- '# - 4%
/ 8 BF &'4+
, :

139. 139
3. . 8 BF &'4+
, : . 2.4. &
8 = 1-1. & , =
8, = : .
- 8 8 8 : L(n) BF n
n
21
2 −
= = ;
( . . 3.38)
% 3.38
- . 1 ' --4 -; $9 "-&8 '$ &-
%#4 6 - : - 7&-& L(n)
8 &--&8 BF
>
66
#.1 . $ ! -
&-- " BF
#&'&-$ " - 1 ' --4
-; $9 "- : '$ &-&
1 1 0,50
2 2 0,125
3 3 0,007 812 5
4 4 0,000 030 517 580
5 5 4,65661*10-10
6 6 1,0842*10-19
4. , 9 = ,
, 9 , 9
= 8 = SAD (
) 4 = SL, 9
= 8.
; 8 =
, 9 , : 8
; . ) ,
= ; = K
8 8 BF ( . 2.4 .2.5) 8

140. 140
& - 1& % 0% # 3
. 8
8 8. .
8 8 8.
! 8 8
3 8 8
8 ; 8
, : :
1. )$ $# #.-$ % 1 6 0&9 4 6 - 3-, '$ 1 -, #$5 &0-$' -&8 5 # &8
; -19 " $ & ; -19 " 2#48 05 #.2 --4 0-$' --4 5$0& - !
1 ; 9 =- $ .
. 8 ; ; =
8 = 4-9%
9 , : ; ; = , =
8 BF ;
BF (%# BF). + 8 =:
. 8 : , 9
.
. ; ;
= .
! ;
; %# BF.
. 8 ; «0» ;
«1».
: .
" : CS 8 ,
8 .
+ 8 = .
8 BF.
8 BF ; ; = :

141. 141
!
= .
. ;
= nK → .
2. )$ $# #.-$ % 1 6 0&9 4 6 - 3-, '$ 1 -, #$5 &0-$' -&8 5 # &8
; -19 " $ & ; -19 " 2#48 0 -2 --4 0-$' --4 5$0& - ! 1 ; 9 =- $
.
. 8 ; ; =
= 8 BF ; %# BF.
+ 8 =:
& ; %# BF, 9 .
3 %# BF , 9 = = 8.
8 BF ; ; = :
& ; .
& : .
3. $ &'-&" % 6$ $# #.- : % 1 6 0&9 : 6 - 3-, '$ 1 -,
#$5 &0-$' -&8 5 # &8 ; -19 " $ & ; -19 ".
" = ; 2 8
8. . = 8 BF ;
8 %# BF ;
= =1..n.
+ = , 9 =
8:
. , =
, 9 : .
. 8 –
8 ,
=
+ 8 4,7
8 8.

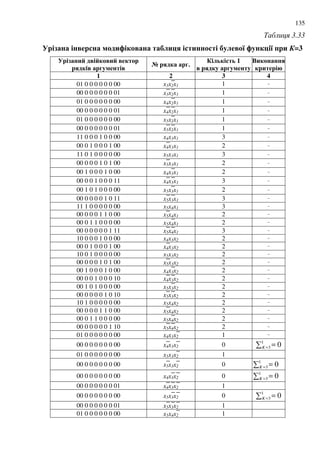
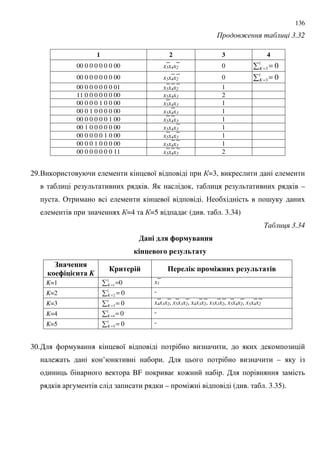
142. 142
' , , =
8 BF Sad, Sl, Ss , ;
8. + 8 8 PO SBF &'4+
= SM 8 SBF
= 8
8 SBF : ,
8. $ = 8 PO SBF
&'4+ = 8 BF
; 9 8 BF. $ =
8 ChO BF &'4+ =
BF 9
8 BF.
" [6, 7, 8, 10, 11, 12, 13, 14, 15, 17, 18, 22, 24,
26, 27, 29, 30, 32]

143. 143
( 4
) -) ) ( ,
+ , ( , * )
+ ) *
4.1 = 6 &'&-&, < 6 #.-33 . &- 0 %& 1 -&8 6 & : , <
4 . #&1 1 #.1 . 8 %-&8 &!-$#
4.1.1 0 #. $ & % # %7 -. 6 &'&-, < 6 #.-33 . &- 0 %& 1 -&8
6 & : -$ $6 - 0$9 :
; :
(07), 9 , =
BF, 8 . . 07 =
( $) n xi m BF yi:
=
=
=
),...,,(
...
),...,,(
),...,
2
,
1
(
11
21
2122
nnn
n
xxxfy
xxxfy
n
xxxfy
& 8 BF f(n), 9
, = : 8 .
= , 9 = ; =
( . . 2.1.3.2). + :
,
, , ; 8 BF f(n) = , 9
, ;
.
> 8 BF : ,
, , , 9 = BF. %
: 8 %#
BF:

144. 144
0 02& - : BF [4]. ' ; %# BF = '= ,
8 8 BF
BF &'4+. =
2n
, n – BF. n
BF = ( . . 4.1):
' 4.1
($# 7- . 0 $--4 1 #.1 4%1 $5#&9 &-- 5 # : ; -19 :
% 1 #.1 $ ! -
> 66 #.1 . $ ! - BF #.1 . 4%1 $5#&9 &-- BF
1 5 32
2 16 65 536
3 24 16 777 216
4 32 4 294 967 296
5 64 1,84467*1019
… … …
#$ &-- 3 0$# 7- 3 0 $--4 1 #.1 8 7#& &8 5$0& -&8 '$ &-
i 6 & 0 $-- 0-$' --4 5$0& - ! 1 ; 9 =- $ K
. + K=1 BF = 2Ln (i. #
; = K
; = . % n=16
(i ( . . 4.2). .
BF : %#
BF ( : %# BF). # ;
; 8 %# BF (i BF
; = : 8 BF . 4 ,
= ; %#
BF = K
$ , 9 :
8 BF . . ; ;
BF ; (i
= K

145. 145
, 9 8, ;
8
' 4.2
($# 7- . 0 $--4 1 #.1 5$0& -&8 '$ &- i 5 # : ; -19 :, 41$
& . 16 $ ! - , % 0-$' --4 5$0& - ! 1 ; 9 =- $ K
>
66
(-$' --4
K
#.1 .
K
) &
−Φ
Φ
=∆
1K
K + #$ %#4 5'& # --4 1 #.1
K %#4 $ ! - n=16
1 1 32 - nzn
K ⋅==
= 216
1
2 2 480 15,000
−
=
=
= ⋅=
1
1
16
2 4
n
i
n
K iz
3 3 4480 9,333
−
=
=
= −−⋅⋅=
2
1
16
3 )1(4
n
i
n
K iniz
4 4 29120 6,500
−
=
=
= −−⋅⋅=
3
1
16
4 )1(8
n
i
n
K iniz
5 5 139776 4,800
−
=
=
= −−⋅⋅=
4
1
16
5 )1(384
n
i
n
K iniz
6 6 512512 3,667
−
=
=
= −−⋅⋅=
5
1
16
6 )1(1792
n
i
n
K iniz
7 7 1464320 2,857
−
=
=
= −−⋅⋅=
6
1
16
7 )1(6656
n
i
n
K iniz
8 8 3294720 2,250
−
=
=
= −−⋅⋅=
7
1
16
8 )1(19968
n
i
n
K iniz
9 9 5857280 1,778
−
=
=
= −−⋅⋅=
8
1
16
9 )1(48810
n
i
n
K iniz
10 10 8200192 1,400
−
=
=
= −−⋅⋅=
9
1
16
10 )1(97622
n
i
n
K iniz
11 11 8945664 1,091
−
=
=
= −−⋅⋅=
10
1
16
11 )1(159744
n
i
n
K iniz
12 12 7454720 0,833
−
=
=
= −−⋅⋅=
11
1
16
12 )1(212992
n
i
n
K iniz
13 13 4587520 0,615
−
=
=
= −−⋅⋅=
12
1
16
13 )1(229376
n
i
n
K iniz
14 14 1966080 0,429
−
=
=
= −−⋅⋅=
13
1
16
14 )1(1966080
n
i
n
K iniz
15 15 524288 0,267
−
=
=
= −−⋅⋅=
14
1
16
15 )1(131072
n
i
n
K iniz
16 16 65536 0,125
−
=
=
= −−⋅⋅=
15
1
16
16 )1(65536
n
i
n
K iniz

146. 146
8 8
:
1. + = K ; (i
= :
. $ : , 9
= (i =
, = , 9 =
, = ( 10% 30%)
2. $ ; %# BF,
8 BF. + ; , 2
3. + 8 ’
= K=1. + 8 : , ; p
BF 8, 3.3. ) 9
p K=i (i=1,2,…,n) ;
=
=
−
=< 1
2iQ
iK
in
p , , . % 8
= ,
= ; 1=iQ
4. ! ; 8 BF
; (i, BF 1=iQ
0=iQ .
= 8 . ;
(i = , =8 . $
; : 8 ’ , 8,
8
+ ; 8,
, ; = , - ,
8

147. 147
4.1.2 06$ $# #3 $--4 6 9 - 0$9 : 5 # &8 ; -19 ", < 4 .
#&1 1 #.1 . $ ! - , 41 - -&" '&--&1 6 & 1 --4
6 9 # ! '- ! 6 1 $--4 9&; &8 5# 1
; ; 8 BF, 9
, = 8 –
8 ; : .
! 8 ,
’ = BF:
= 8 8, 9 =
88 , : :
: ;
BF, ,
: (i, 9 ’ 8
8 8 8;
, ’ = 8:
= K :
(i, 9 ’ 8, = 9 ’=
8 ’ . ' 8 8
’ = 8 . %
8 = : : ’= ,
9 : 8 ’ +
+ 8 PO CHO BF, PO CHO BF =
: = 8
. / 8
BF = ( . . 4.1).
= 8 BF,
8

148. 148
' . 4.1 / 8 BF BF, 9
, ;
8 PO BF =
BF = K, 9 :
8 8 8

149. 149
8 CHO BF =
BF, ,
: 8. . ;
8 CHO BF = , ’
8 BF 8 =
: BF
# BF = BF,
, . ;
8 = ; . / ,
8, :
. . =
, = : 8
.
4.2 1 $ $6$ $ - -6 ! $ - ! 1 6# 1 &- 0 %& 1 -&8
6 & : , < 4 . #&1 1 #.1 . 8 %-&8 &!-$#
4.2.1 ) &0-$' --4 $6$ $ - -6 ! $ - ! 1 6# 1
/ - ( &"+2( $) 8 ,
9 , 8
:
1. $ 8 8 BF
;
2. $ 8 8
BF ;
3. $ 8 8 BF
;
4. $ 8 8
BF

150. 150
, ’ 8 :
5. 4 : 8
6. + ; BF BF
& 8, 9 =
, = : ’= 8
&"+2( $
' &"+2( $ =:
- PO ( &) BF PO ( &) BF :
;
- 8 , 9
BF ;
- 8 8 SL, SAD, SS, =
$ 07, = , 9
, = : $ 07
4.2.2 + $--4 - 7&- 5 # &8 ; -19 " 0$ :8 6 #.-& & 1 -& &
8$ $1 & &1$ &
4.2.2.1 - $#.-$ -% 1 -$ $ &94 6 $- 1 41 - -&"
- - 5 51& ! 6 #4 & - 5 # &8 ; -19 "
3' 8 BF &'4+. 3' –
BF, 9 = BF, ;
: ; 8 %#
: . BF, 9 : 3',
= 8 BF, ,
- . = .

151. 151
+ : , ’
8 BF &'4+ :
:
3' 8 BF f(n);
; BF 3' BF f(n) –
3';
; 3', 9 : L(n) BF f(n).
. : 3'
, : ’ 3 .
8 ;
BF f(n) 3' 8 .
# ; , 9 : , :
, . & :
= , 9
;
BF – 3'. ! = : ;
, 9
, ’ 8 ; BF – 3', 9
= .
= =
3', : : BF, 9
, = nn
n 2!2 ⋅× , 2n
– %# BF
( : BF). n!*2n
– , 9
: 3'. 8 8
: 8 8 –
BF ( BF %#
8 - ). . ; = :
8 BF, 8 : BF, 9 :
3', = :

152. 152
: :
.
BF f(n) = 2 .
$ n
nn 2!⋅× , n –
BF, n! – :
%# BF, 2n
– : %# BF. ;
BF 9 , :
. %
9 2
( A1)
!
.
/ 8 8
:
1. : %# BF
2. . %#
BF
3. . %# BF
4. ! %# BF
8 8
% 8 8
9 2 ( A2)
, BF f(4)
( . . 4.1, 9
7), = 24
=16 4!*24
=24*16=384 .
= 9
=
8 8 3',
BF, 9 3' ; BF 3' ( . . 4.3).

153. 153
' 4.3
- $#.-$ -% 1 -$ $ &94 6 $- 1 - 7&-& BF,
< 4 . 4 $ ! - &
>> 6'&1 $ &9>
4%1$
$ &9
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
1 15 14 13 12 11 10 09 08 07 06 05 04 03 02 01 00
2 15 14 13 12 07 06 05 04 11 10 09 08 03 02 01 00
3 15 14 11 10 13 12 09 08 07 06 03 02 05 04 01 00
… … … … … … … … … … … … … … … … …
382 00 08 02 10 04 12 06 14 01 09 03 11 05 13 07 15
383 00 04 08 12 02 06 10 14 01 05 09 13 03 07 11 15
384 00 08 04 12 02 10 06 14 01 09 05 13 03 11 07 15
" = BF 3',
9 8 : L(n) BF, 9 n . %
= 1 9 = =
3'. . : ,
: BF 8 3'.
4.2.2.2 &6 $ 6 9 % $ &0-$' --4 - $ $ 1#$% ! 6&
#4 & -
) 9 2.1, 9 3' : BF, 9
BF,
8 8
3'. . 1 %# BF. %
0 : . =
; = 8 3'
, = 0, ,
, ; .
; 3' 8 BF =
8 BF 8 . :

154. 154
8 BF = ; ;
8 .
, BF, 9 = 279 (
0000000100010111), = ( . . 4.4).
' 4.4
) '$ 1 $ $ &94 6 $- 1 - 7&-& BF f(4)
%#4 6 5 % & -$ - 1 -1 - : BF
-$ -&"
1 BF
0 0 0 0 0 0 0 1 0 0 0 1 0 1 1 1
>> 6'&1
> 4%1$
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
1 15 14 13 12 11 10 09 08 07 06 05 04 03 02 01 00
2 15 14 13 12 07 06 05 04 11 10 09 08 03 02 01 00
… … … … … … … … … … … … … … … … …
381 00 04 02 06 08 12 10 14 01 05 03 07 09 13 11 15
382 00 08 02 10 04 12 06 14 01 09 03 11 05 13 07 15
383 00 04 08 12 02 06 10 14 01 05 09 13 03 07 11 15
384 00 08 04 12 02 10 06 14 01 09 05 13 03 11 07 15
8 : BF, 9 : 3', 9 BF 4
279f ,
, = 8:
1. . , = 0.
2. % l – «1» BF 4
279f
= l=5, ; 5 (08, 04, 02, 01, 00).
' ; BF 4
279f .
3. . : –
.
4. . : = ,
. + ; ; 1
5. 8 : 3', :
: BF – 3', ; : 3'
( . . 4.5).

155. 155
. 8 BF 4
279f 3',
8 : BF, 9 : 3', 9 BF,
- 8 8 BF.
' 4.5
0 #. $ 6 5 % & -$ - 1 -1 - : BF
>
))
6 9 $# 0 $-$
-% 1 -$ $ &94
6 $- 1
-$# 7-
+ %
-$ - 1 &
BF, < 8 %4 . BF 10
)
BF 16
)
1 08 04 02 01 00 0000000100010111 279 0117
2 09 05 03 01 00 0000001000101011 555 022B
3 10 06 03 02 00 0000010001001101 1101 044D
4 11 07 03 02 01 0000100010001110 2190 088E
5 12 06 05 04 00 0001000001110001 4209 1071
6 12 10 09 08 00 0001011100000001 5889 1701
7 13 07 05 04 01 0010000010110010 8370 20B2
8 13 11 09 08 01 0010101100000010 11010 2B02
9 14 07 06 04 02 0100000011010100 16596 40D4
10 14 11 10 08 02 0100110100000100 19716 4D04
11 14 13 12 08 04 0111000100010000 28944 7110
12 15 07 06 05 03 1000000011101000 33000 80E8
13 15 11 10 09 03 1000111000001000 36360 8E08
14 15 13 12 09 05 1011001000100000 45600 B220
15 15 14 12 10 06 1101010001000000 54336 D440
16 15 14 13 11 07 1110100010000000 59520 E880
; 3' BF
3' 8 BF f(n) : - ( . . 4.2)
: ’
, ’ 8 3', ; 3'
BF, 9 88 , 3' 8
: L(n) BF f(n).
+ 3' 8 : L(n) BF
: 8 8 :
BF. BF 0
n
2
2 -1. : 8 BF
:
1. + 3'

156. 156
' .4.2 / ; 3' BF
3' 8 BF f(n)
2. . , = 3'.
3. ) 9 , – 3'.
. ; =
3' 8 : L(n) BF, 9 n
; 3' 8 : L(n) BF f(n)
: - ( . . 4.3):

157. 157
' .4.3 / ; 3' BF
3' 8 BF f(n)
& : , 3'
BF ;
=
: , 9 =
9
3'. . ; 3'
= : .
4.2.3 &1 & $--4 ) %#4 &- 0 %& 1 -&8 6 & : -$
- - 0$9 : 6 - 3 &0-$' -&8 5 # &8 ; -19 " 0 #&1&
'& # $ ! -
&"+2( $&" 8 BF f(n)
8 = ; 8 8 8 8.
; 8 = : BF , ;

158. 158
. / &"+2( $
= ( . . 4.4).
/ = :
9. + ; BF f(n)
10. & p BF f(n)
11. ) 9 ; : 8
1
2 −
≥ n
p – 8 BF %# BF, ; ,
9 1
2 −
< n
p – %# BF
12. ! = 8 8
p BF f(n) = K,
8 8
=
=
−
=≥ 1
2iQ
iK
in
p (i=0,1,2,…,n)
+ i =, = K=i,
; iK
j
=
Φ , 1==iK
jQ 0==iK
jQ
13. 8 8 ’=
, iK
j
=
Φ
14. $ iK
j
=
Φ K=i
15. ' iK
j
=
Φ
’=
16. . : : 8
iK
j
=
Φ , 1==iK
jQ 0==iK
jQ
17. K=i
iK
j
=
Φ , 1==iK
jQ ( 8 ) ,
0==iK
jQ ( , 9 )
18. $ iK
j
=
Φ K=i+1, ;
8 , = 8
, 9

159. 159
' . 4.4 / 8 PO BF &'4+
; ’= 1
19. + 8 7-10 = =i+1, i+2,...,n
Φ ,

160. 160
1=Q ( 8 ) , 0=Q ( ,
9 )
20. Φ , 8 ,
BF f(n) , =
; 8
21. &
3' A1
4.2.4 &1 & $--4 ) %#4 &- 0 %& 1 -&8 6 & : -$
- - 0$9 : & 6 - 3 &0-$' -&8 5 # &8 ; -19 " 0
#&1& '& # $ ! -
&"+2( $&" BF f(n)
8 = : 8 BF ; 8
8. &"+2( $ = ,
BF, 9 : .
/ &"+2( $ =
( . . 4.5).
. = :
1. + ; BF .
2. : 8 BF f(n), 9 : , p
3. . ’= ,
BF
4. : 8 BF f(n), 9 : ,
iK
j
=
Φ K=i
5. : 8 BF f(n), 9 : ,
iK
j
=
Φ ’=
6. . : BF f(n), 9 : , : 8
iK
j
=
Φ , 1==iK
jQ 0==iK
jQ

161. 161
7. : 8 BF f(n), 9 : , K=i
iK
j
=
Φ , 1==iK
jQ ( 8
) , 0==iK
jQ ( , 9
)
' . 4.5 / 8 PO BF &'4+
; ’= 1
8. : 8 BF f(n), 9 : , 9 ;
: 8 1
2 −
≥ n
p –
%# BF, ; , 9 1
2 −
< n
p – %# BF

162. 162
9. : 8 BF f(n), 9 : ,
= K, 8 8
=
=
−
=≥ 1
2iQ
iK
in
p (i=0,1,2,…,n)
10.! – : , BF,
8 = K
11. : 8 BF f(n), 9 : ,
iK
j
=
Φ K=i+1, ; 8 ,
= 8 , 9
12.+ 8 7-11 = = i+1, i+2,...,n
Φ , 1=Q
( 8 ) , 0=Q ( , 9
)
13. : 8 BF f(n), 9 : , Φ ,
8 , BF
f(n) 8 8
14.$ BF f(n), 9 :
. +
8 BF
15.&
3' A1
4.2.5 &1 & $--4 ) %#4 &- 0 %& 1 -&8 6 & : -$
- - 0$9 : '$ 1 &0-$' -&8 5 # &8 ; -19 " 0 #&1&
'& # $ ! -
&"+2( $&" 8 BF f(n)
8 8 9

163. 163
8 8 = . /
= ( . . 4.6).
. = :
9. + BF f(n)
10. & p l
BF f(n)
11. ) 9 lp ≥ – ; %# BF,
; , 9 lp < – ; %# BF
12. ! = 8 8
8 : 8 p ( «*»)
BF f(n) = K,
8
in
iK
Q
iKp −
=
=
=
≈
=+≥ 2*1i
(i=0,1,2,…,n)
+ i =, = K=i,
; iK
j
=
Φ , 1==iK
jQ 0==iK
jQ
13. 8 8 ’=
, iK
j
=
Φ
14. $ iK
j
=
Φ K=i
15. ' iK
j
=
Φ
’=
16. . : : 8
: iK
j
=
Φ , 1==iK
jQ 0==iK
jQ
:
8 8 8 %# BF
− 1==iK
jQ → in
iK
Q
iK
−
=
=
= =+ 2*1j
, =
= >1j
0Q
iK , i=0, 1, ..., n
− 0==iK
jQ → =
= =0j
0Q
iK , = >*
0iK , i=0, 1, ..., n
8 8 8 %# BF

164. 164
− 1==iK
jQ →, =
= =0j
0Q
iK = >*
0iK , i=0, 1, ..., n
− 0==iK
jQ →, in
iK
Q
iK
−
=
=
= =+ 2*1j =
= >1j
0Q
iK , i=0, 1, ..., n
' .4.6 / 8 CHO BF &'4+ ;
’= 1

165. 165
17. K=i
iK
j
=
Φ , 1==iK
jQ ( 8 ) ,
0==iK
jQ ( , 9 )
18. + : BF
: BF
19. : 8 8 BF
iK
j
=
Φ K=i+1, ; 8 8
8 BF, = 8
, 9
20. + 8 7-11 =
=i+1, i+2,...,n
Φ , 1=Q ( 8 ) ,
0=Q ( , 9 )
21. Φ , 8 ,
BF f(n) , =
; 8
BF
22. &
3' A1
4.2.6 &1 & $--4 ) %#4 &- 0 %& 1 -&8 6 & : -$
- - 0$9 : & '$ 1 &0-$' -&8 5 # &8 ; -19 " 0
#&1& '& # $ ! -
/ 8 &'4+ =
( . . 4.7). . = 8 :
1. ! CHO BF .
2. . , BF (m) =
: : CHO BF (n1, n2, …, nm)

166. 166
' .4.7 / 8 CHO BF &'4+ ;
3. . , : CHO BF ; –
: 8 BF ; %# BF
4. $ : 8 BF iΦ =1,
= ; 8 8 BF
5. + , = 8 ,
: BF, 8

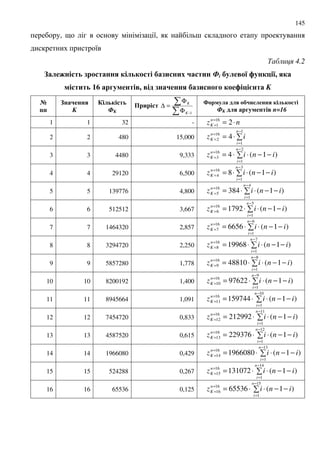
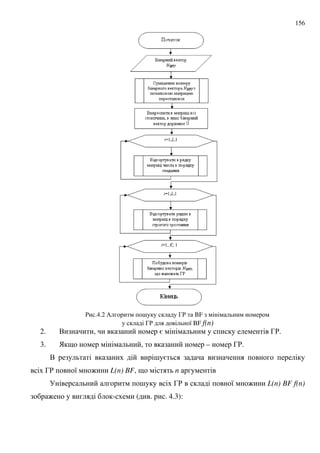
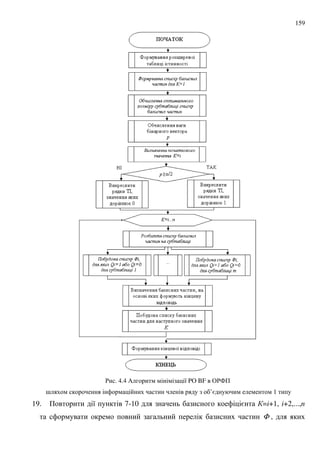
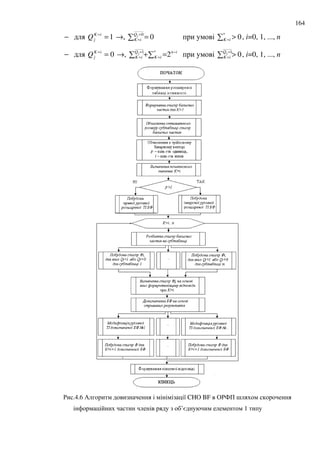
167. 167
6. : CHO BF
BF : 8 CHO BF 8
7. . 8 ; 8 %# BF
8. + : 8 8 BF iΦ
, = ; 8
8 BF
9. 8 , = =n
10. 8 : 8 BF
" 4 : 8 BF
11. &
3' A1
4.3 % $ 2&; $#.- ! 6 & 3 9 # ! 6 & #.- ! 1 % $--4
-; $9 :
4.3.1 ($!$#.-$ 5 % $ 2&; $#.- ! 6 & 3 6 & #.- !
1 % $--4 -; $9 :
& ; : ; 8 = ,
8. /
8 9 8 20-
; ’ [34-38]
8 8 .
+ 8 = , 9
8 = ; .
8 ; 8 [38]
: =
; ( . . 4.5).

168. 168
% 4.5
($# 7- . 0 $--4 1 #.1 $ $- 6 & #.- ! 1 % $--4
6 & 0 $-- 0 4%- &!-$# , < 6 %$= . 4
> 66
0 4%- .
&!-$# , <
6 %$= . 4
#.1 . $ $-
6 & #.- !
1 % $--4
1 2 24
2 3 40320
3 4 2,09228*1013
4 5 2,63131*1035
5 6 1,26887*1089
& = 8 =, ,
: &'4+ BF, 8 8 8
8 8 ;
8 8 .
$ ; :
, 9 8 , , }7,...,2,1,0{ arg
7
arg
2
arg
1
arg
0 ==== aaaa .
; = ;
. ; 3 (n=3):
38loglog 22 === Nn ,
N – ,
n – ;
;
8 8 ( . . 4.6), },...,,{ arg
7
arg
1
arg
0 aaa –
, },...,,{ 710
ininin
aaa – 8 , 9 : :
.
$ in
f1 , in
f2 , in
f3
.
4 = :

169. 169
=
=
=
),,(
),,(
),,(
arg
3
arg
2
arg
133
arg
3
arg
2
arg
122
arg
3
arg
2
arg
111
fffFf
fffFf
fffFf
in
in
in
(5.1)
% 4.6
) &1#$% 6 & #.- ! 1 % $--4 -; $9 :
> 6 '$ 1 !
& #
-$ -&" 1 %
6 '$ 1 ! & #
-$ -&" 1 % & # ,
< 6 %$= . 4
> & # , <
6 %$= . 4
arg
0a 0 0 0 0 1 1 arg
30 aain
=
arg
1a 0 0 1 1 1 0 arg
61 aain
=
arg
2a 0 1 0 0 0 1 arg
12 aain
=
arg
3a 0 1 1 1 1 1 arg
73 aain
=
arg
4a 1 0 0 0 1 0 arg
24 aain
=
arg
5a 1 0 1 0 0 0 arg
05 aain
=
arg
6a 1 1 0 1 0 0 arg
46 aain
=
arg
7a 1 1 1 1 0 1 arg
57 aain
=
N
arg
3f
N
arg
2f
N
arg
1f
N
in
f1
N
in
f2
N
in
f3
) '$ 1 ; -19 :
$ ! -
+ -19 : 1 % $--4
= , 9
= ; , 9 = ( 3=n ). . ,
8 822 3
==n
.
' . 4.8 !

170. 170
# ; =
, 9 : , 9 = , =
– .
. , , 9 = ,
( . . 4.8):
1. 7 .
in
if : ;
, 9 = .
2. " ; in
if .
, 9 , .
. .
8 8 –
( . . 4.7).
% 4.7
) &1#$% 6 & #.- ! % 1 % $--4 -; $9 :
>
0$1 % $- !
& #
-$ -&" 1 %
0$1 % $- ! & #
-$ -&" 1 %
% 1 % $- ! & #
> % 1 % $- !
& #
arg_
0
in
a 0 0 0 1 0 1 arg
5
arg_
50 aaa inout
==
arg_
1
in
a 0 0 1 0 1 0 arg
2
arg_
21 aaa inout
==
arg_
2
in
a 0 1 0 1 0 0 arg
4
arg_
42 aaa inout
==
arg_
3
in
a 0 1 1 0 0 0 arg
0
arg_
03 aaa inout
==
arg_
4
in
a 1 0 0 1 1 0 arg
6
arg_
64 aaa inout
==
arg_
5
in
a 1 0 1 1 1 1 arg
7
arg_
75 aaa inout
==
arg_
6
in
a 1 1 0 0 0 1 arg
1
arg_
16 aaa inout
==
arg_
7
in
a 1 1 1 0 1 1 arg
3
arg_
37 aaa inout
==
N
arg_
3
in
f
N
arg_
2
in
f
N
arg_
1
in
f
N
out
f1
N
out
f2
N
out
f3
) '$ 1 ; -19 : %#4
% 1 % $--4 -; $9 :
+ -19 : % 1 % $--4
$ out
f1 , out
f2 , out
f3
.

171. 171
4 = :
=
=
=
),,(
),,(
),,(
arg_
3
arg_
2
arg_
133
arg_
3
arg_
2
arg_
122
arg_
3
arg_
2
arg_
111
inininout
inininout
inininout
fffFf
fffFf
fffFf
(5.2)
! =
, : .
8 8 =
, 9 = ( . . 4.9):
1. 7 . + –
8 ; .
2. " ; out
if . +
; in
if .
3. 7 .
= –
.
' . 4.9 !
4.3.2 % $ 5# 1 5'& # --4 ; 1 $- ! 1#3'$ % 1 % $--4
& –
: out
f1 , out
f2 , out
f3

172. 172
in
f1 , in
f2 , in
f3 8 : .
: = : . . =
. ; , 9 n ,
: n! . ! ; 8 :
/ n
n 2⋅ ( 3 – 24
). . ,
; , 8
( & $74) [12].
% & $74 n
n 2⋅ n
n 2⋅
. #
n
n 2
2 ⋅
%# & $74 = n! ( n=3
. . 4.8).
% 4.8
$5#&94 &-- & & '$ 1 &0-$' -&8 5 # &8 ; -19 "
%#4 0 ’401 0$%$' & $--4 0 - ! ; 1 $- ! 1#3'$ 2&; $--4
(-$' --4 4%1 $ ! -
(-$' --4 '$ 1 &0-$' -&8
5 # &8 ; -19 "
> 4%1$
$5#&9
&-- in
f1
in
f2
in
f3
out
f1
out
f2
out
f3
0 00000000 00000000 00000000 ******** ******** ********
1 00000000 00000000 00000001 ******** ******** ********
2 00000000 00000000 00000010 ******** ******** ********
3 00000000 00000000 00000011 ******** ******** ********
… … … … … … …
1 006 644 00001111 01011100 00110100 ******** ******** ********
1 006 645 00001111 01011100 00110101 00001111 11000101 01010011
1 006 646 00001111 01011100 00110110 00001111 11000101 01100011
1 006 647 00001111 01011100 00110111 ******** ******** ********
… … … … … … …
16 777 213 11111111 11111111 11111101 ******** ******** ********
16 777 214 11111111 11111111 11111110 ******** ******** ********
16 777 215 11111111 11111111 11111111 ******** ******** ********
8 in
if = ; . %
3 { in
f1 , in
f2 , in
f3 } : 24-
%# & $74. . { out
f1 , out
f2 , out
f3 }

173. 173
%# & $74. ) 9
, 8 ( *). ) ,
& $74, = 24 , 24
BF. %# & $74 = 16 777 216 , 40 320 =
.
: f(x1,x2,x3,…,x24) & $74 =
:
0,24%%100
2
!8
%100
2
!
24
=⋅=⋅= n
n
k
n – :
{ in
if , out
if } (n=8); k – BF
% ’ = 8 ( . . 4.9).
% 4.9
0 #. $ & - 0$9 : ! -$#.- " ; 6 % $ # --4
>
66
& $-- 0 #. $ &
SL SAD
#.1 .
-&8
$-0&
1
$
8 8
967 680 40 320 1 008 024
2
$
8
169 100 9 873 178 997
3 $ 8 17,47% 24,48% 17,75%
8 ; 8 ;
, 9 : ; .
124 ’ , 9 8. '
8 8 8
8 .
: , 9
4,47%.
4.3.3 % $ % # 2&; $--4 in
if /% 2&; $--4 out
if

174. 174
" ; ( , ; )
, 9 ,
( . . 5.1). .
( . . 5.2). & ,
9 = 8 8 . $
},,{ arg
1
arg
2
arg
3 fff },,{ 321
ininin
fff .
; , 9 n ,
= n.
},,{ arg
1
arg
2
arg
3 fff =:
===
===
===
HEXDECBIN
HEXDECBIN
HEXDECBIN
AAf
CCf
Ff
17010101010
20411001100
024011110000
arg
1
arg
2
arg
3
,
},,{ 321
ininin
fff =:
===
===
===
HEXDECBIN
in
HEXDECBIN
in
HEXDECBIN
in
Df
Bf
CAf
814110001101
12700011011
20211001010
3
2
1
$ = ,
= ; 8 :
HEXDECBIN DBCA 8113245325110101101110001100101000 ==
" ; =
: 8
},,{ 321
ininin
fff .
+ 8 },,{ arg
1
arg
2
arg
3 fff 8
. . 8 =
, ,
, , ; ,
},,{ 321
ininin
fff = . % = in
fi

175. 175
},,{ 321
ininin
fff = , 9 n
2
, ; , 9 = . n=3
– 70,
40320!2!2 3
==n
.
9 , , 9 =
, ( . . 4.7), =
( . . 4.9):
,
: ; &1, &2 &3
in
fi },,{ 321
ininin
fff ;
; &1, &2 &3 , 9
; . + = .
: = 8 in
fi
, 9 in
fi (70 )
' . 4.9 ! ;

176. 176
# = ;
. %
; 8 – 8
; = :
9 .
" ; in
fi
n, 9 .
2 BF n
( . . 4.10). %
= ; ; = ’=
8 in
fi
% 4.10
($# 7- . 0 $--4 1 #.1
-$5 ; -19 " 1 % $--4 in
fi
6 & 0 $-- '& #$ n
> 66
#.1 . 0 --&8 n
; -19 : 1 % $--4
in
fi
#.1 . -$5
; -19 " 1 % $--4
},...,,{ 21
in
n
inin
fff
1 2 24
2 3 40 320
3 4 2,09228*1013
4 5 2,63131*1035
5 6 1,26887*1089
1 $#.-& 6& $--4 =
; , ’ 8 ,
= ; .
% ,
’ BF .
% BF, 9 8 },...,,{ 21
in
n
inin
fff ,
= – ,
3' BF , 9
in
fi . + ’= BF ; [83].

177. 177
’= BF = : ’= 8
; ( . . 4.11) BF [84].
% 4.11.
6 %- 2 --4 -$6 - --4 6 - : - 7&-& L(n) 5 # & & ; -19 4 & $
! 6$ & #4 & -
- . xi
BF
L(n)
#.1 . BF L(n) #.1 . L(n)
% 1
1 6- --4,
%
2 24
= 16 5 31,250000
3 28
= 256 22 8,593750
4 216
= 65.536 402 0,613403
5 232
= 4.294.967.296 1.228.158 0,028595
6 264
G 1,84467·1019
400.507.806.843.728 0,002171
+ : L(3) , 9 3 , 70 BF,
= . BF
’= 6 3' ( . . 4.12). ;
= : ’= 70 BF 6 , , ,
70 6
% 4.12
1#$% ! 6 #4 & - - 7&- L(3) 5 # &8 ; -19 ", 41&8
5 -$ - 1 = %-$1 $ 1 #.1 . - # %&-&9.
>
66
>
- .
BF, 41
8 %4 .
>> BF,
< -$# 7$ .
1 15 6 15, 51, 85, 170, 204, 240
2 23 8 23, 43,77, 113, 142, 178, 212, 232
3 27 24
27, 29, 39, 46, 53, 58, 71, 78, 83, 92, 114, 116, 139, 141, 163, 172, 177, 184,
197,202, 209, 216, 226, 228
4 30 24
30, 45, 54, 57, 75, 86, 89, 99, 101, 106, 108, 120, 135, 147, 149, 154, 156, 166,
169,180 198, 201, 210, 225
5 60 6 60, 90, 102, 153, 165, 195
6 105 2 105, 150

178. 178
) , ; &1, &2 &3, 9 ;
70 BF in
fi , ; 6 3' BF
in
fi AA15, 23, 27, 30, 60, 105. . , 8
3' BF 3'.
% ; ( .
. 5.3) 8
; &1, &2 &3 ( . . 4.10). " = : =
; .
' . 4.10 !
;
! 8 3' = : BF,
9 : 3' [2, 3, 4], ,
; ; ; :
BF.
. : = , 9 3' BF in
fi
8 – =

179. 179
,
; – 8 , 9
= BF 3'.
' . 4.11 8 8
3' A23
, 3' A23 8 BF ( . . 4.13). ) , 9 =
3', 6 jic . ( . . 4.11),
% 4.13
- $1 & 6 %1#3' --4 6 #4 &0$9 "-&8 8 % 5’=%-$- " 8
) %1#3' --4 6 #4 &0$9 "-&8 8 %>
66
> BF
1.1c 2.1c 1.2c 2.2c 1.3c 2.3c
1 23 3x 2x 3x 1x 2x 1x
2 43 3x 2x 3x 1x 2x 1x
3 77 3x 2x 3x 1x 2x 1x
4 113 3x 2x 3x 1x 2x 1x
5 142 3x 2x 3x 1x 2x 1x
6 178 3x 2x 3x 1x 2x 1x
7 212 3x 2x 3x 1x 2x 1x
8 232 3x 2x 3x 1x 2x 1x
: , : 8 BF = =
8 ; . $
jic . 8 8 BF 3' A23 4.13.
8 3' 8 8 8 3'
; , 8
. ; = ; 3' ; BF
3'

180. 180
> 3' = 6 3' ( . . 4.13). ' ;
:
GR
l
N≥1
2
36loglog 221 ≥=≥ GRNl
1l –
8 3', GRN – 3'
> BF 3' = 24 BF
( . . 5.8). ' ; :
524loglog 222 ≥=≥ BFNl
2l –
8 BF 3', BFN –
BF 3'
% ; , 9 ’= =
; &1, &2 &3 24- (3 3
8 3' 5 8 BF).
$ , , = , 9
. :
, 9 9 ; , = ,
3' ( . . 4.14)
% 4.14
$5#&94 6 %1#3' --4
2&-& 6 $ # --4 $
2&-& 6 $ # --4 BF %&-
?&-$ 6 $ # --4 ?&-$ 6 $ # --4 BF %&->
66
> BF
GR0 GR1 GR2 BF0 BF1 BF2 BF3 BF4
1 23 1 1 1 * * 0 0 0
2 43 1 1 1 * * 0 0 1
3 77 1 1 1 * * 0 1 0
4 113 1 1 1 * * 0 1 1
5 142 1 1 1 * * 1 0 0
6 178 1 1 1 * * 1 0 1
7 212 1 1 1 * * 1 1 0
8 232 1 1 1 * * 1 1 1

181. 181
. , 9 = 3' 23 =
( . . 4.12). / 3' AA 15, 27, 30, 60, 105.
$ = ; 8. $ ;
8, 2
2 3' BF – 5 . %
=
= LS 9,69 ,
ADS – 2,27
' . 4.12 ; , 9 =
3' A23
4.4 % $ 2&; $#.- ! 6 & 3 '$ &-- ! 6 & #.- ! 1 % $--4
-; $9 :
$ 8 = ;
: . / =
2 = , 9 : : :

182. 182
1. + = . %
9 = , 9 9 =
8.
2. 4 = : ; " , 9
. % : +4
n
n 2!< , 9 ; : 8
& ; 8 =
; , 9 8
.
. >+, 9
>+, 9 = , 9 = , « » ( ,
:
) = ; : ; .
% 4.15
%&- 0 $ $- 1 % $--4 -; $9 :
0$ % 6 ! 3 0$= - : % 1 6 0&9 : & #
>
66
& #, <
6 %$= .4
$2&--&" 1 % & # , <
6 %$= . 4, % 1 % $--4
$2&--&" 1 % & # , <
6 %$= . 4, 6 #4 1 % $--4
1 in
a5
inininininininin
aaaaaaaa 0.051.052.053.054.055.056.057.05
~
0.05
~
1.05
~
2.05
~
5.05
~
7.05 *** ininininin
aaaaa
2 in
a9
inininininininin
aaaaaaaa 0.091.092.093.094.095.096.097.09
~
0.09
~
1.09
~
2.09
~
5.09
~
6.05
~
7.09 ** inininininin
aaaaaa
3 in
a7
inininininininin
aaaaaaaa 0.071.072.073.074.075.076.077.07
~
0.07
~
1.07
~
2.07
~
3.05
~
5.07
~
6.09
~
7.07 * ininininininin
aaaaaaa
4 in
a3
inininininininin
aaaaaaaa 0.031.032.033.034.035.036.037.03
~
0.03
~
1.03
~
2.03
~
3.09
~
4.05
~
5.03
~
6.07
~
7.03
inininininininin
aaaaaaaa
5 in
a11
inininininininin
aaaaaaaa 0.111.112.113.114.115.116.117.11
~
0.11
~
1.11
~
2.11
~
3.07
~
4.09
~
5.11
~
6.03
~
7.11
inininininininin
aaaaaaaa
6 in
a13
inininininininin
aaaaaaaa 0.131.132.133.134.135.136.137.13
~
0.13
~
1.13
~
2.13
~
3.03
~
4.07
~
5.13
~
6.11
~
7.13
inininininininin
aaaaaaaa
7
- - *****
~
3.11
~
4.03
~
6.13
ininin
aaa
8
- - ******
~
3.13
~
4.11
inin
aa
9
- - *******
~
4.13
in
a

183. 183
+ >+ < = , 9
, ( " ) 8
" . = " { }inininininin
aaaaaa 13113795 ,,,,, . ) 9
( . . 4.15),
9 , 9 : = 1 n (n -
" ). + = : - " . . 2
«*» .
/ = RS- .
% 9 , 9 : ’ n
9 . .
) $!$ & =:
1. , 9 : ; . %
: ; .
2. + , 9 =
.
3. )!!1...)!2()!1(!(2 ⋅⋅−⋅−⋅⋅ nnnn
, n –
" .
& - 1& % 0% # 4
. ,
8 . +
&"+2( $ : , 9
8 8, ’
8 8.
= 8 , 9
,
8 ; ;
8 .

184. 184
& -
8 , 9 . .
- . ' &"+2( $ =:
- +& ( &) BF +& ( &) BF :
;
- 8 , 9
BF ;
- 8 8 SL, SAD, SS, =
$ 07, = , 9
, = : $ 07
& , 9 = .
& :
8 8
;
8 8
;
8 8
;
8 8
.
' ;
8. & ;
8. & , ,
8 . ! ;
: . 8
.
! ;
8 8 = .
" [12, 14, 15, 16, 28, 29, 30]

185. 185
. 8 ; : - 9
8 8
(&'4+):
1. . ; 8 8
; = ’ :
8 8 8 8 8
: 8 : , 8
, 9 8
8 ; 9
: .
8 <
8
.
2. . ; 8
8 8
; 8 8, 9
; 8
. 8 -
8 -
8 .
3. & ; 8
8 ;
8 , 9
9 8 ,
, ,
8.

186. 186
4. : : :
- &'4+, =
= ’ :
= 8 8
. = : : =
8 SL, SAD, 9 = SS:
i. 10%
;
ii. 32%
;
iii. 2
, 9 : A1;
- : 8 :
, 9 = : ; :
: ’= 8 :
. : 8 :
= : : 8, :
. & :
; , : =8 :
= ; ;
- 8 &'4+ –
8 8, 9 = : 4,7
8
8 8 ; ;
; = ;
- 8
, = :
8 , 9 -
- . +

187. 187
8, 9
= 8;
- 8
8 , 8 :
8 : , 8.
' : : + «&',!& - /.I3/0I)»
. ! " 8 .
. ; - "
8 , 8 8 8 20.12.2013 A179
„& : ; :
, 8 8
8 2014–2018 ”, . 1.2.9.1. “' 8
8 8 ”, -
8 “. ;
” ( :
= 8 0109U001880), .

188. 188
)
1. @.&. $ 9
8 (3'). / @.&. ,
$...7 , #...$ // . :
. – 2011, A 4 − . 39-41.
2. @.&., " ; „ 8
” / @.&. , $...7 , #...$ // .
: . – 2012, A 1 − . 32-34.
3. @.&. + 9 :
(24) / @.&. , $...7 , #...$ . $
«+ . # » // . . – 2012,
A 18 (231) − . 93-97.
4. @.&., $ 9
/ @.&. , $...7 , #...$ . //
«' C » – 2012, A 2 (57) − . 67-69.
5. @./., '
– 9 D. / @./. , (. .+ ,
$./.3 , $...7 // . :
. – 2012, A 4 − . 25-28.
6. @./. " D . /
@./. , $...7 , $.4./ . // ' C D
D D, 2012, A4, .110-116
7. @./., " D D
/ @./. , $...7 ,
$.4./ . // + C . – 2013, % 12. A3, .413-420
8. @./., " D D
/ @./. , .. .' ,
$...7 // B D D D
D . (.D 2).
" . – . – 2013, .87-100

189. 189
9. @.&., : –
COGNATE- 8. / @.&. , $.&. 9, $...7 // .
: . – 2013, A 1 − . 20-23.
10. @./., " D 9
D / @./. , $...7 , (. .+ //
. : . – 2013, A 2 − . 33-39.
11. 7 $... ' D 9
D D /
$...7 // ' C D D D, – 2013, A4 (63), –
.109-115
12. ' .. ., '
D D ;
D . / .. . ' , $...+ , $...7 // .
% . – 2014, A 1 − . 27-30.
13. 7 $... + 8
.
/ $...7 // . : . –
2014, A 2 − . 67-73.
14. ' .. ., , D
D ; D D / .. .' ,
$...7 , $...3 // :
/ . .. .' , ..)." . – 6 : , - &&&
«* », – 2014. – . 146-176.
15. ' .."., &
; / ..".' , $...7 , &.$.> ;
// . : . – 2015, A 1 − . 97-
102.
16. ' .."., 3 ;
/ ..".' , $...7 , /.".% , &.$.> ; //

190. 190
. : . – 2015, A 2 − . 99-
105.
17. 7 $..., + ;
C D
D / $...7 , (. .+ // . +
. $ : % . – 2015, A
1 − . 189-195.
18. 7 $..., + &.7., " 8
8 8
/ $... 7 , &.7. + .// $... – 2015, A 1 − . .
19. 7 $..., + &.". +
(24) / $...7 , &.".+ //
# 8 , : : 8
- 8 8, 25-27 2012 – , 2012. – % 1. –
$. 141–142.
20. 7 $..., + (. . 2 D
D / $... 7 , (. . + //
$ ,
: V# : 8 - 8
8, 19-21 2012 – ! :: , 2012. – . 246-247.
21. 7 $... + &.". >
/ $...7 , &.".+ // 4 -
8 , , - :
II- 8 : 8 - 8 8, 25-27 : 2012
– , 2012. – $. 102–103.
22. 7 $... + &.". $ ,
/ $...7 ,
&.".+ // / ’ - 8
: , , : 8 8

191. 191
- 8 Internet- 8, 18-22 2013 , . , ,
2013. – $. 4–5.
23. + '.&., 7 $... ' MINFORM
/ '.&. + , $...7 //
/ ’ - 8 : ,
, : 8 8 -
8 Internet- 8, 18-22 2013 , . , , 2013. – . 6–
7.
24. 7 $..., + (. . $ D D
D
/ $... 7 , (. . + // ' C :
66# : D : -
«B » 17- " : : ,
22-24 2013 ., – 6 , 6 'B, 2013. – $. 70-71.
25. 7 $..., 9 $./. / C Cognate-
D Extended Data Mining / $...
7 , $./. 9 // & :
IV : 8 - 8 8, 22-24 2013 – ,
2013. – $. 41–42.
26. 7 $... "
- 9 D / $...
7 // + D : D I :
- , 19-20 2013 – D- -
% -+ , 2013. – $. 80.
27. ..&., 7 $... / -
8 8 / ..&. , $...
7 // / ’ - 8
: , , : 8 8
- 8 Internet- 8, 17-21 2014 ., . , ,
2014. – . 13–15.

192. 192
28. 7 $... .
; 8 / $... 7 // /
’ - 8 : , ,
: 8 8 - 8 Internet-
8, 16-20 2015 ., . , , 2015. – . 48–49.
29. 7 $... . = ;
/ $... 7 // ## :: ,,
:: 8 8 - 8 8, 16
2015 ., . , , 2015.
– . 102-103.
30. 7 $...
; / $... 7 // # , , .
#"/:2015: - 8 8, 20-25 2015
., . $ , $ : , 2015. – . 152.
31. 7 $..., + &.". &
;
: / $... 7 , &.". + // +
: . :
8 8 - 8 8 , ,
, 20-24 2015 ., . " , + :
, 2015. – . 122.
32. 7 $... +
D D
/ $... 7 // $ D D C :
D 6VIII . - D D
: D , 9 120- 9 ,
6-8 2015 ., . , $ D , 2015. – . 255-
259.
33. McCluskey E.J. Essential multiple–output prime implicants / E.J. McCluskey,
H. Schorr // Microwave Res. Inst. Symp. ser. 12. – 1962. – '.437 – 457.

193. 193
34. McCluskey E.J. Minimization of Boolean functions / E.J. McCluskey // Bell
Syst. Techn. J. – 1956. – 35. – A6 . – '. 1417 – 1444.
35. Reed I. S. A class of multiple–error–correcting codes and decoding scheme //
IRE Trans. Inform. Theory. 1954. IT-4.
36. Reed I.S. A class of multiple-error-correcting codes and the decoding scheme.
Transactions of the IRE Professional Group on Information Theory / I.S. Reed // IRE
Trans. Inform. Theory. – 1954. – V. 4. – A 9. – P. 38 – 49.
37. Sasao T. Complexity Measures for AND–EXOR Expressions / T. Sasao //
Proc. 3rd International Workshop on Applications of the Reed–Muller Expansion in
Circuit Design. – Oxford (UK). – 1997. – P. 145–156.
38. D. E. Muller. Application of boolean algebra to switching circuit design and
to error detection. // IRE Transactions on Electronic Computers, 3:6–12, 1954.
39. Shannon C. E. A Mathematical Theory of Communication // Bell System
Technical Journal. – 1948. – %. 27. – $. 379—423, 623—656.
40. Shannon C. E. Communication in the presence of noise // Proc. Institute of
Radio Engineers. – Jan. 1949. – %. 37. – A 1. – $. 10—21.
41. > . ' D . / .> –
".: , - D, 1963. – 830 .
42. > . B. ' D . / .
B.> – ".: , - . ., – 1963. – 468
43. Jürgen Alex. Konrad Zuse: der Vater des Computers / Alex J., Flessner H.,
Mons W. u. a.. – Parzeller, 2000. – 263 S.
44. Raúl Rojas, Friedrich Ludwig Bauer, Konrad Zuse. Die Rechenmaschinen
von Konrad Zuse. / Raúl Rojas, Friedrich Ludwig Bauer, Konrad Zuse – Berlin: Springer,
1998. – Bd. VII. – 221 S.
45. Zuse K. Der Computer mein Leben. ( .) The Computer / K.Zuse –
Berlin:My Life. – Springer Verlag, 1993. – 251 S.
46. " X. : . / / X." // . –
A 1. – 1990 – .31-37.

194. 194
47. Colossus: The First Electronic Computer: The Secrets of Bletchley Park's
Code-breaking Computers / B. Jack Copeland OUP Oxford, – 2006 – 462 .
48. / 3.$. +
? / 3.$./ , 3.$.7 // / D
. – 1975. – A 6. – $.6–10.
49. ? ,.,. & D :
/ ,.,. ? // " "
9 . – 1927. – %.354. – $.9 – 28.
50. ? ,.,. / / ,.,. ?
// " " 9 .– 1928. – %.35.
– .311 – 373.
51. 3 ; ..". $ D / ..".3 ; – ".:
4 . – 1962. – 476 .
52. 3 ; ..". . . / ..".3 ; – : , -
/ $$', 1964.
53. 3 ; ..". . /$ . / ..".3 ; – : % , 1972.
– 312 .
54. 3 ; ..". & D : . /..".3 ; – ".:
, 1982. – 552 .
55. + . /. / D D D ;
. / . /.+ – ".: .D ;. ; , 1970. – 308 . .
56. + . /. 2 D ,
, . / . /.+ – ".:B – 1974 . – 368 .
.
57. + , . /. 2 -
/ ./.+ . – ".: B , 1981 . – 232 .
58. + . /. " : . & D
D D . / ./.+ . – ".: ' , −1989,-184
59. + . /. . D D /
./.+ . – ".: $ , 1977, 280 .

195. 195
60. + . /. $ : % . /
./.+ . – ".: . – 3 . . - . ., 1986.-288
61. + . /. . D D. / ./.+ . – ".:
B , 1970 – 88
62. + . /. , D 80-
// , 1994, A 4, . 74-95.
63. + +.$. & ;
/ +.$. + // $ .
.– . & – D D . –
%.2. – 1884.
64. ! /. . ' D D
? / /. . ! // D / 7. –1995. – %.39. – A3. – $.5 – 8.
65. ! /. . 7D D ? ,
9 D D / /. . ! // /
D . – 1995. – A4. – $.36 – 41.
66. ! /. . " D D
? / /. . ! // / . – 1996. –
A5. – $.134 – 140.
67. Zakrevskij A. Minimum polynomial implementation of systems of
incompletely specified Boolean functions / A. Zakrevskij // Proceedings IFIP WG 10.5
Workshop on Applications of Reed–Muller Expansion in Circuit Desing. – 1995. – Chiba,
Japan. – '.250 – 256.
68. ! /. . " D D
? / /. . ! // / . – 1996. –
A5. – $.134 – 140.
69. ! /. . & 9 ; D
D / /. . ! // ' . – 1964. – 7. – A1. –
$.166 – 174.

196. 196
70. ! /. . & ; D /
/. .! // $ . «+ D D ». – 1967. – ".:
. – $.84 – 95.
71. ! /. . 2 D / ! /. . –
".: . – 1981. – 416 .
72. ! /. ., % .'. + D
D . / /. .! .'.% – ": . 2012. – 200 .
73. ! /. ., % .'. + D
D . / /. .! , .'.% . , 3 – "- :
( '$$. – 2012. – 200 .
74. ! /. ., % .'. " D
D 4. , D . /
/. .! , .'.% . // + . – 2009, A 1 −
. 5-14.
75. ! /. . / : .
/ /. .! . // . % . ,
D . – 2011, A 3 − . 94-99.
76. ! /. . & 9
. / /. .! . // . %
. + : . – 2005, A 14 − . 13-17.
77. ! /. . : : C
D. / /. .! , .'.% . // +
. – 2012, A 2 − . 100-104.
78. ) $... & D / $...
) // " . .– 1952. – %. 30. – A 2. – $.329 – 345.
79. ) $... . . 4- . /
$...) . – ".: , – 2003. – 384 .
80. 7 +. . $ D +2"- $7,$ /
7 +. . – " . : i C , 1992. – 232 .

197. 197
81. 7 +. ., ( $... $ D
/ +. . 7 , $... ( . + . /. .! .
– " .: , – 1987. – 189 ., .
82. Naumov L., Shalyto A. Automata Theory for Multi-Agent Systems
Implementation // Proc. Of Integration of Knowledge Intensive Multi-Agent Systems. —
Boston (MA). — 2003 // http://is.ifmo.ru, « ».
83. / ..2., 3./., > D /./. D
9 . / ..2./ , 3./. , /./.> D . –
2.: B , – 1981. – 165 .
84. ! (./., > D /./. " D
D . – $+ .: $+ 3 ,%"&, 2003 //
http://is.ifmo.ru, «+ D».
85. > D /./. 2 . " D
: " / /./.> D : – $+ .: , – 2000. – 780
c.
86. / ..2., 3./., > D /./. D
9 . / ..2./ , 3./. , /./.> D . –
2: B . – 1981. . – 168 ., .
87. .. +., > D /. /. ' D
D // /
. 1996. A1. 158-170
88. $ .. . D
: / .. . $ // , . / $$$'. %
. – 1989. – A3. – $.187 – 191.
89. $ ..+. $ : D
D / ..+. $ // . – % 5. –
.D 2. – 1993. – $.111 – 115.
90. $ $. . & : D
D , 9 / $. . $ //
. – % 16. – .D 2. – 2004. – $.117 – 120.

198. 198
91. $ $. . & : D
D / $. . $ // . –
% 14. – .D 2. – 2002. – $.48 – 53.
92. / ..2. ' D
/ ..2. / , .. . , /./. > D // /
. – 1988. – A4. – $.138 – 147.
93. .. . ' D
D / .. . , /./. > D //
/ . – 1993. – A3. – $.135 – 151.
94. 3 3. +., .. 7. 4 D D
+ . /3.+.3 , .. 7. . – ".: , – 1966. – 120 .
95. Miller J.F. Highly efficient exhaustive search algorithm for optimizing
canonical Reed–Muller expansions of boolean functions / J.F. Miller, P. Thomson // Int. J.
Electronics. – 1994. – vol.76. – '.37–56.
96. Sarabi A. Fast exact and quasi–minimal minimization of highly testable
fixed–polarity AND–EXOR canonical networks / A. Sarabi, M.A. Perkowski //
Proceedings of the 29th
ACM/IEEE Design Automation Conference. – 1992. – California.
– '. 30–35.
97. Sasao T. Exact minimization of AND/EXOR expressions using multitreminal
EXOR ternary decision diagrams / T. Sasao, F. Izuhara // IFIP WG. 10.5 Workshop on
Applications of the Reed–Muller Expansions in Circuit Design. – 1995. – Japan. – '. 213–
220.
98. Sasao T. Representation of logic functions using EXOR operators / T. Sasao //
IFIP WG.10.5 Workshop on Applications of the Reed–Muller Expansions in Circuit
Design. – 1995. – Makuhari. – Chiba, Japan. – P.11 – 22.
99. Blake A. Canonical expression in Boolean algebra. Dissertation, Chicago. –
1937.
100. Quine W.V. A way to simplify truth functions / W.V. Quine // Amer. Math.
Mon. – 1955. – 62. – A9. – '. 627–631.

199. 199
101. Quine W.V. The problem of simplifying truth functions / W.V. Quine //
Amer. Math. Mon. – 1952 59. – '. 521 – 531.
102. Quine W.V. On cores and prime implicants of truth functions / W.V. Quine //
Amer. Math. Mon. – 1959. – A9. – '.755 – 760.
103. Quine W. The Problem of Simplifying Truth Functions / W.Quine //
American Mathematical Monthly. 1952. Vol. 59. P. 521–531.
104. McCluskey E. Minimization of Boolean Functions. / E. McCluskey //The Bell
System Technical Journal, November 1956. Vol. 35. P. 1417–1444.
105. ? @.,. & D . . . / @.,.
? // $ . . :., 1960. – 1. – A4. – $.609 – 611.
106. / $.".. / D D
. / $.". / . + . &.2. 7 . – ": ' , – 1987. 136 .,
.
107. '. ". $ . . / '. ". . – ": ' , –
1965. $. 220—232.
108. B '.B. ' D 4 : : ./
' B B . – ": «" », 1985, – 260 .
109. @./. . D
D D D / @./.
, . . + , .2. // $ . . / D;
, C . 3.(. + . – 2 . –1998. –
..3. – $.94 – 99.
110. @./. D D D
: – . " / @./. , . .
+ , .2. // , C .
3.(. + , . – D. – 1999. – 195 .
111. + . . / D :
/ . . + // $ . . . , –
C / D. – D. – 1998.– A6. – $.122 – 130.

200. 200
112. .2. /
9 D /
.2. // $ . . . , – C
/ D. – D. – 1998.– A6. – $.114 – 122.
113. Kochkarev J.A. Minimization of logic function in the optimized form of
representation / J.A. Kochkarev, N.N. Panteleyva, N.L. Kazarinova // $omputer systems
(ASC’98). – Szczecin (Poland). – 1998. – '.567 – 568.
114. @./. / D D D
– D / @./.
, . . + , .2. // B . – 1999. – A6,
%.1. – $.217 – 221.
115. @./. / D
/ @./. , .2. , . .
+ // ! “$
8 : = ”.($ .: “.
”) – .: 4/ /, 2% . – 1999. – ..6.
– $.429 – 432. –.
116. @./. 9 :
, D D / @./.
, . . + // B . – 2001. – A11. – $.81 – 86.
117. @./. "
/ @./. , (. . + // .
: .– 2005. – A4. – C.94-99.
118. @./. $ ; D D
/ @./. , (. . + , $./. > // B . – . – 2006. –
A1. – $.82-86.
119. @./. $ ; D D
D / @./. , (. . + //
$ D $$+&,-2005: D IX

201. 201
" : - $$+&,-2005. – D. –
2005. – $.167-169.
120. @./. & D D
+2" Exchanged DATA Mining (EDM) / @./.
, (. . + // . :
. – 2006. – A2. – $.7-10.
121. @./. $
D / @./. , (. . + , .$.
// ! . –
. – 2009. – A32. – $.171-177.
122. @.&. / : 8 ' -
" 8 / @.&. , $.&.
9, &.". + // . : .
– 2010. – A2. – $.64–68.
123. @.&. (
’ 8 / @.&. , $.&. 9, &.". + // / .
/ . B D D. – 6 . – 2010. –
A1(25). – $.132-136.
124. @.&. + (&/
'(/ / @.&. , $.&. 9, &.". + // #
; ISDMCI’2010:
: 8 8 (ISDMCI’2010). – O . – 2010. – $. 85-86.
125. @./., + (. . & C
D D D
D // - : «+ C ».
, 6 C , A2 (%
10), 2010, . 295-299.
126. @./. , C D
D D / @./. , (. . + //

202. 202
# 8 , : VII . 8 - .
., 4-6 . 2010 . : . – ., 2010. – $.81.
127. @./. . :
/ @./. , (. . + , ,... $ //
. : . – 2011. – A1. – $.45–
49.
128. + . 10201 8 , "+ G 06 F 7 / 544. +
/ @.&., + &."., > $.&. – A u200502059; . 05.03.05;
. 15.11.05, 7 . A11.
129. + . 42063 8 , "+ G 06 F 7 / 48. / @.&.,
.$., + &.". – A u200814795; . 22.12.08; . 25.06.09, 7 .
A12.
130. @.&. +
D / @.&. , &.".
+ // , D D -2006: D II :
- +$. – ) . – 2006. – $.52-56.
131. @.&. & ;
8 / @.&.
, #... $ , &.". + // # 8 #"%-
2009: ## : 8 - 8 8 (#"%-2009). –
. – 2009. – $. 38-39.
132. Kochkarev Y.A. Ortogonal forms of presentation of boolean functions in
device blocks / Y.A. Kochkarev, I.I. Osipenkova, E.N. Panasko // , D
D +$ – 2009: D : -
. – ) . – 2009. – $.39-42.
133. @./. & D D D /
@./. // , . ' . – ' – – . – 1980. – 191 .
134. @./. % ,
D D D : . …
. : 05.13.13 / @ / . – % , 1983.

203. 203
135. @./. & D
Extended Data Mining /
@./. , ,... $ // D «, D D
». 19–20 2006 . $ D . + :
: «6 ». – & . – 2006. – $.24-27.
136. @./. , D :
EDM / @./. , .... 7 , .$. //
. : . – : % . –
A 1 – 2. – 2007. – $.60 – 65.
137. @./. / :
D EDM / @./.
, ,... $ , .$. // " D # : -
(,"% 2008). – D. – C.20 – 24.
138. @./. % ,
D D ./
, 9 9 %
. .. . D . – % , 1983
139. @./., + (. ., $ ,... '
/ @./. , (. .+ ,
,...$ // . % . – 2011, A 1 − . 45-49.
140. Kochkarev Y.A., Osipenkova I.I., Panasko E.N. Ortogonal forms of
presentation of boolean functions in device blocks / Y.A.Kochkarev, I.I.Osipenkova,
E.N.Panasko // . : .- 2009.-
$ – .39-42.
141. @./., + . ., .2. . D
D D D
D //$ . . /, -
C / D. – , – 1998. – .35-38.
142. @./., 9 $./. +
// B , , A6, 2011, $.73.

204. 204
143. @./., 9 $./. % COGNATE- 8
// . : , A3, 2011,
$.35-38.
144. @./. & D D D /
@./. // , . ' . – ' - - . – 1980. – 191 .
145. @./., 9 $./. ' -
D // B
, , A4, 2012, $.73.
146. @./., + (. ., $ ,... . :
// .
: . – A1. – 2011.
– $.45-49
147. , @. /. & D D D
[% ] / @. /. . % . . - . – ' / : , - ' . -
, 1980. – 191 .
148. , @./. , D :
EDM [% ]/ @./. , ....
7 , .$. // . :
. – 2007. – A 1 – 2. – $.60 – 65.
149. @./. & D D
9 P / @./. , . .
+ , .2. // B . – 2002. – A14.
– $.106 – 108.
150. + &.". " -
/ &.". + // >
. %.> : . . – 2005. – $.151-152.

205. 205
& /%& /

206. 206

207. 207

208. 208

209. 209