Le document décrit deux algorithmes de recherche d'un entier dans un tableau: la recherche séquentielle et la recherche dichotomique. La recherche séquentielle examine chaque élément du tableau un par un, tandis que la recherche dichotomique divise le tableau en sous-parties pour localiser plus rapidement l'élément, nécessitant que le tableau soit préalablement trié. Les deux algorithmes incluent des procédures pour saisir les données et retourner si l'élément est présent ou non.

1. Réalisé par: Jihen DAMERJI
Algorithmes de recherche d’un
élément dans un tableau

2. Mise en situation

4. Activité
On désire écrire un programme
RECHERCHE qui permet de vérifier
l’existence d’un entier P dans un
tableau T d’éléments positifs de N
entiers avec N dans l’intervalle [5..20]

6. Recherche séquentielle

7. 1
• Consulter les éléments de la liste
2
• les comparer un à un avec l’élément recherché, du debut jusqu’à
trouver l’élément ou arriver à la fin de la liste
3
• Ceci est réalisé à l’aide d’une structure itérative

10. Analyse du programme principale
Résultat=
si x=vrai alors
ecrire(p,' existe dans le tableau')
sinon
ecrire(p,' n''existe pas dans le tableau');
Finsi
Xfn existe(n,p,t)
Proc saisie(n,p,t);
Fin recherche

11. Algorithme de la fonction existe
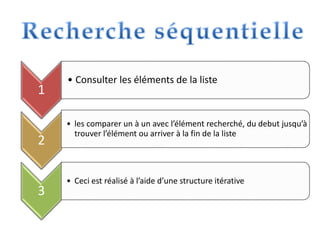
0) Def fn existe (n,p: entier ; t :tab) : booleen
1) verif  faux
i0
répéter
ii+1
si t[i]=p alors
verif vrai
Finsi
Jusqu’à (verif=vrai) ou (i=n)
2)existeverif
3) Fin exixte

14. program sequentielle ;
uses wincrt ;
type
tab = array [1..20] of integer ;
var
t : tab ;
n,p : integer ;
x : boolean ;

15. procedure saisie ( var n,p : integer ;var t :tab);
var
i : integer ;
begin
repeat
writeln('Saisir la taille du tableau :'); readln(n);
until n in [5..20];
for i:= 1 to n do
Begin
repeat
writeln('Saisir l''élement ',i); readln(t[i]);
until t[i] > 0 ;
end;
writeln('saisir un entier :'); readln(p);
end;

16. function existe (n,p: integer ; t :tab) : boolean ;
Var
i : integer ; verif : boolean ;
begin
verif := false ;
i:=0 ;
repeat
i:=i+1;
if t[i]=p then
verif:=true ;
until (verif=true ) or (i=n) ;
existe:=verif ;
end;

17. begin
saisie(n,e,t);
x:=existe(n,e,t);
if ( x=true ) then
writeln(e,' existe dans le tableau')
else
writeln(e,' n''existe pas dans le tableau');
end.

18. Mise en situation

20. Activité
On désire écrire un programme
RECHERCHE qui permet de vérifier
l’existence d’un entier P dans un
tableau T trié de N entiers.

22. Recherche dichotomique

23. 1
• Comparer P avec l’élément du milieu du tableau.
2
• Si P< milieu alors chercher P dans la partie gauche. (tri
croissant)
• Si P> milieu alors chercher P dans la partie droite.
3
• Refaire le même travail jusqu’à trouver P ou bien
arriver à la fin du tableau.

24. Remarque :
Cette technique ne peut être utilisée qu’avec
une série de données déjà triée.

27. Analyse du programme principal
Résultat=
si x=vrai alors
ecrire(p,' existe dans le tableau')
sinon
ecrire(p,' n''existe pas dans le tableau');
Finsi
Xfn existe(n,p,t)
Proc saisie(n,p,t);
Fin recherche

28. Algorithme de la fonction existe
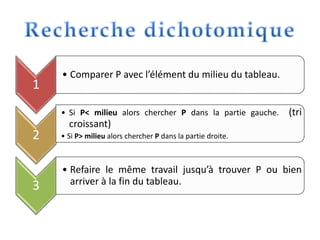
0)def fn existe (n,e :entier ; t :tab) : boolean ;
1) x:=faux
bi:=1
bs:=n
repeter
mil(bi+bs) div 2
Si t[mil] = e alors x vrai
Sinon si t[mil] < e alors
bi mil+1
Sinon bs mil-1
finsi
finsi
jusqu’à (x= vrai) ou (bi >= bs)
2)existe x
3) Fin existe

31. program dichotomique ;
uses wincrt ;
type tab = array [1..20] of integer ;
var t : tab ; n,e,m : integer ; x : boolean ;
procedure saisie ( var n,e : integer ;var t :tab);
var i : integer ;
Begin
repeat
writeln('Saisir la taille du tableau :'); readln(n);
until n in [5..20];
for i:= 1 to n do
begin
Repeat
writeln('Saisir l''élement ',i); readln(t[i]);
until t[i] > 0 ;
end;
writeln('saisir un entier :'); readln(e);
end;

32. function existe (n,e : integer ; t :tab) : boolean ;
var i,bi,bs : integer ;
x : boolean ;
Begin
x:=false ; bi:=1 ; bs:=n ;
repeat
mil:=(bi+bs) div 2
if t[mil] = e then
x:=true
else if t[mil] < e then
bi:=n+1
else
bs:=n-1 ;
until (x=true) or (bi >= bs) ;
Existe:=x;
end;

33. Begin
saisie(n,e,t);
x:=existe(n,e,t);
if x=true
Then
writeln(e,' existe dans le tableau')
Else
writeln(e,' n''existe pas dans le tableau');
end.