Le document présente une série d'exercices mathématiques pour des élèves de lycée, incluant le calcul de longueurs dans un rectangle, l'identification de nombres appartenant à Z, ainsi que des propriétés des fonctions polynomiales. Il contient également des instructions sur des devoirs à rendre et des corrections d'exercices. Les élèves doivent démontrer leur compréhension des inéquations et des surfaces dans des problématiques appliquées.

1. Mme REZGUI
Lycée Sainte Claire, Lille
2020-2021

2. Groupe α Groupe ∆ Groupe λ
15 10 15

3. Groupe α Groupe ∆ Groupe λ
5 10 10

4. Exercice 1: ABC est un rectangle en B avec AB = 1km et
BC = 4 km.
a. Calculer la valeur exacte de la longueur AC (en km)
b. Donner un encadrement d’amplitude 10−3
de AC, puis
sa valeur arrondie à 10−3
c. Donner un encadrement au millimètre de AC, puis sa
valeur arrondie au millimètre. 17 = 4,123105626
Exercice 2: Parmi les nombres suivants quels sont ceux qui
appartiennent à ℤ
𝐴 = 4
−12
7
:
3
14
𝐵 = 3 − −4 + 5 ∗ 8 𝐶 = 3
1
3
−
3
4
−
5
6
Exercice 3 : Si elle existe, donner une écriture décimale de
chacun des nombres suivants.
D =
3
15
−
1
5
∗
2
10
E= -2,62 * 10−3
F =
6
4
∗
6
2
G = 1+
3
4
∶
7
3

5. Propriétés des fonctions
x, 𝒙𝟐
et 𝒙𝟑
(P1)
Automatismes : Interpréter une valeur absolue
Le cours : Les propriétés des fonctions x, 𝒙𝟐et 𝒙𝟑
À retenir : Interpréter une valeur absolue
Contenu à copier du tableau
Contenu à copier du tableau
Contenu à copier du tableau

6. Automatismes : Interpréter une valeur absolue
𝑥 − 𝑎 ≤ 𝑟
𝑥 < 𝑎
𝑥 ≤ 𝑎
𝑥 ≥ 𝑎
𝑥 > 𝑎
𝑎
−𝑎
Exemple (livre):
Savoir-faire 3 page 19

7. 𝒙 -∞ -4 -2 -1 0 1 2 4 +∞
𝒇 𝒙 = 𝒙
x
f(x)
2- Tableau de variation de la fonction carrée𝒇 𝒙 = 𝒙
1- Tableau de valeur de la fonction𝒇 𝒙 = 𝒙
3- Courbe de la fonction𝒇 𝒙 = 𝒙
O i
x
j
y
4- Dé𝐟𝐢𝐧𝐢𝒓 𝒍𝒂 𝒇𝒐𝒏𝒄𝒕𝒊𝒐𝒏 𝒄𝒖𝒃𝒆 𝒇 𝒙 = 𝒙

8. 𝒙 -∞ -4 -2 -1 0 1 2 4 +∞
𝒇 𝒙 = 𝒙𝟐
x
f(x)
2- Tableau de variation de la fonction carrée𝒇 𝒙 = 𝒙𝟐
1- Tableau de valeur de la fonction𝒇 𝒙 = 𝒙𝟐
3- Courbe de la fonction𝒇 𝒙 = 𝒙𝟐
O i
x
j
y
4- Dé𝐟𝐢𝐧𝐢𝒓 𝒍𝒂 𝒇𝒐𝒏𝒄𝒕𝒊𝒐𝒏 𝒄𝒖𝒃𝒆 𝒇 𝒙 = 𝒙𝟐

9. 𝒙 -∞ -4 -2 -1 0 1 2 4 +∞
𝒇 𝒙 = 𝒙𝟑
x
f(x)
2- Tableau de variation de la fonction carrée𝒇 𝒙 = 𝒙𝟑
1- Tableau de valeur de la fonction𝒇 𝒙 = 𝒙𝟑
3- Courbe de la fonction𝒇 𝒙 = 𝒙𝟑
O i
x
j
y
4- Dé𝐟𝐢𝐧𝐢𝒓 𝒍𝒂 𝒇𝒐𝒏𝒄𝒕𝒊𝒐𝒏 𝒄𝒖𝒃𝒆 𝒇 𝒙 = 𝒙𝟑

10. Devoir:
Copier sur son cahier les 2 fiches de cours suivantes (livre page 186):
• La fonction carré
• La fonction cube

11. À retenir : Interpréter une valeur absolue
𝑥 − 𝑎 ≤ 𝑟
𝑥 < 𝑎
𝑥 ≤ 𝑎
𝑥 ≥ 𝑎
𝑥 > 𝑎
𝑎
−𝑎
Exemple (livre):
Savoir-faire 3 page 19

12. Groupe α Groupe ∆ Groupe λ
15 10 15

13. Groupe α Groupe ∆ Groupe λ
5 10 10

14. Exercice 1: ABC est un rectangle en B avec AB = 1km et
BC = 4 km.
a. Calculer la valeur exacte de la longueur AC (en km)
b. Donner un encadrement d’amplitude 10−3
de AC, puis
sa valeur arrondie à 10−3
c. Donner un encadrement au millimètre de AC, puis sa
valeur arrondie au millimètre. 17 = 4,123105626
Exercice 2: Parmi les nombres suivants quels sont ceux qui
appartiennent à ℤ
𝐴 = 4
−12
7
:
3
14
𝐵 = 3 − −4 + 5 ∗ 8 𝐶 = 3
1
3
−
3
4
−
5
6
Exercice 3 : Si elle existe, donner une écriture décimale de
chacun des nombres suivants.
D =
3
15
−
1
5
∗
2
10
E= -2,62 * 10−3
F =
6
4
∗
6
2
G = 1+
3
4
∶
7
3

15. Utilisations des propriétés
des fonctions x, 𝒙𝟐et 𝒙𝟑 (P2)
Automatismes : interpréter une valeur absolue
Le cours : utilisation des propriétés des fonctions x, 𝒙𝟐et 𝒙𝟑 (P2
À retenir : Interpréter une valeur absolue
Contenus à copier du tableau
Contenu à copier du tableau
Contenu à copier du tableau

16. https://www.geogebra.org/m/rNjzASEc#material/FSYppRC8
Utilisations des propriétés
des fonctions x, 𝒙𝟐et 𝒙𝟑 (P2)
Correction des exercices:
Page 190: 59; 60; 64 (a. et d.);

17. À retenir : Interpréter une valeur
absolue
𝑥 − 𝑎 ≤ 𝑟
𝑥 < 𝑎
𝑥 ≤ 𝑎
𝑥 ≥ 𝑎
𝑥 > 𝑎
𝑎
−𝑎
Exemple (livre):
Savoir-faire 3 page 19

18. Groupe α Groupe ∆ Groupe λ
15 10 15

19. Groupe α Groupe ∆ Groupe λ
5 10 10

20. Correction Interrogation n°1:
Manipuler les nombres réels
Automatismes :
Le cours : Correction de l’interrogation 1
À retenir :
Aucun continu
Contenus à copier du tableau
Aucun continu

21. Correction Interrogation n°1:
Manipuler les nombres réels
Correction au tableau

22. À retenir : Interpréter une valeur
absolue
𝑥 − 𝑎 ≤ 𝑟
𝑥 < 𝑎
𝑥 ≤ 𝑎
𝑥 ≥ 𝑎
𝑥 > 𝑎
𝑎
−𝑎
Exemple (livre):
Savoir-faire 3 page 19

23. Groupe α Groupe ∆ Groupe λ
15 10 15

24. Groupe α Groupe ∆ Groupe λ
5 10 10

25. Fonctions: Modéliser et
résoudre une problématique
Automatismes :
Le cours : Correction de l’interrogation 1
À retenir : Manipuler des inéquations
Aucun continu
Contenus à copier du tableau
Contenus à copier du tableau

26. Fonctions: Modéliser et
résoudre une problématique

27. Problématique: Air de la
fenêtre > 0,9 𝑚2

28. 1. ℎ 𝑥 = 2 − 2,5𝑥 + 𝑥
= 2 − 1,5𝑥
2. 𝑙 𝑥 = 𝑥 + 𝑥 = 2𝑥
3. méthode1:
𝑎 𝑥 = ℎ 𝑥 ∗ 𝑙 𝑥 −
𝑥 ∗ 2𝑥
2
= 2 − 1,5x ∗ 2x − 𝑥2
= 4x − 3𝑥2
− 𝑥2
= 4𝑥 − 4𝑥2

29. 3. méthode2:
𝑎 𝑥 = 𝑙 𝑥 ∗ 2 − 2,5𝑥 +
𝑥 ∗ 2𝑥
2
= 2 − 1,5x ∗ 2x − 𝑥2
= 4x − 5𝑥2
+ 𝑥2
= 4𝑥 − 4𝑥2

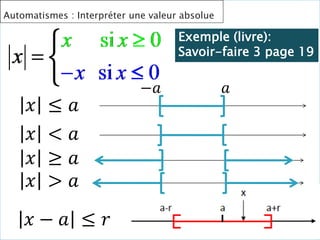
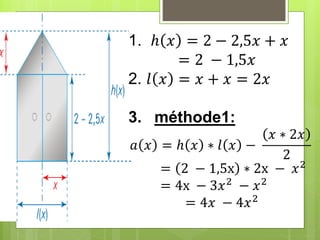
30. 4. La courbe de 𝑎 𝑥 = 4𝑥 − 4𝑥2
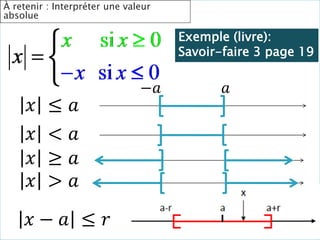
𝒂 𝒙 = 𝟎, 𝟗 𝑝𝑜𝑢𝑟 𝑥 = 0,35 𝑜𝑢 𝑥 = 0,65
𝒂 𝒙 ≥ 𝟎, 𝟗 𝑠𝑢𝑟 𝑙′
𝑖𝑛𝑡𝑒𝑟𝑣𝑎𝑙𝑙𝑒 [0,35 ; 3,65]
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1.1
1.2
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5 0.55 0.6 0.65 0.7 0.75 0.8 0.85 0.9 0.95 1
a(x)

32. 0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1.1
1.2
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5 0.55 0.6 0.65 0.7 0.75 0.8 0.85 0.9 0.95 1
a(x)
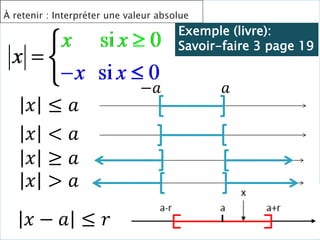
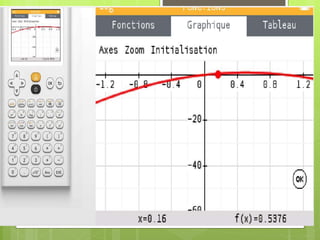
5. La courbe de 𝑎 𝑥 = 4𝑥 − 4𝑥2
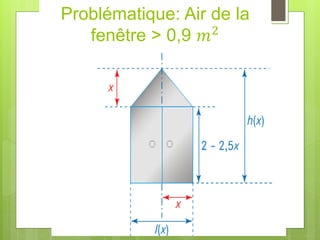
L’air de la fenêtre est supérieur à
0,9𝒎𝟐
𝒑𝒐𝒖𝒓 𝒙 𝒅𝒂𝒏𝒔 [𝟎, 𝟑𝟓 ; 𝟑, 𝟔𝟓]

33. Problématique: Pour quelles valeurs
de x la surface du logo est-elle
supérieure à 18𝑐𝑚2

34. 1. A x = 𝑥 ∗ 4 − 𝑥
= 4x − 𝑥2
2. ℎ 𝑥 = 5 ∗ 4 − 𝐴 𝑥
= 20 − 4𝑥 + 𝑥2
= 𝑥2
−4𝑥 + 20

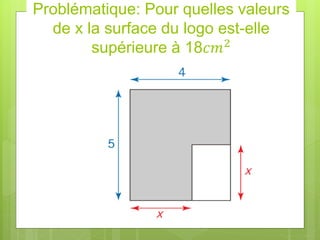
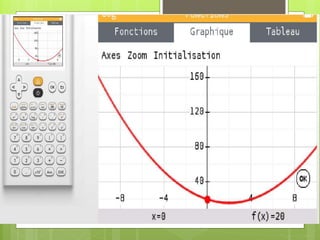
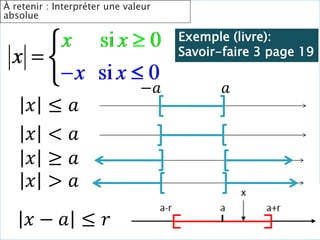
36. 5. ℎ 𝑥 ≥ 18
𝒉 𝒙 ≥ 𝟏𝟖 𝒑𝒐𝒖𝒓 𝒙 𝒅𝒂𝒏𝒔 [0 ; 0,58] ∪ [3,42 ; 4]
0
2
4
6
8
10
12
14
16
18
20
22
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5
h(x) = 𝑥^2 −4x+ 20

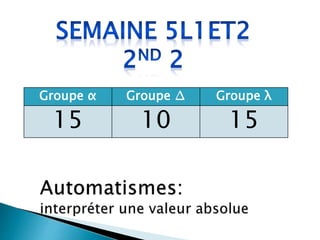
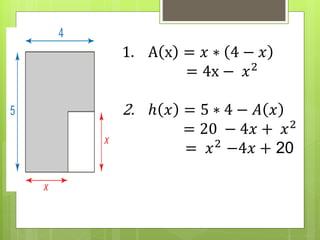
37. 𝒍𝒂 𝒔𝒖𝒓𝒇𝒂𝒄𝒆 𝒅𝒖 𝒍𝒐𝒈𝒐 ≥ 𝟏𝟖 𝒎𝟐
𝒑𝒐𝒖𝒓 𝒙 𝒅𝒂𝒏𝒔 [0 ; 0,58] ∪ [3,42 ; 4]
6. l𝑎 𝑠𝑢𝑟𝑓𝑎𝑐𝑒 𝑑𝑢 𝑙𝑜𝑔𝑜 ≥ 18 𝑚2
0
2
4
6
8
10
12
14
16
18
20
22
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5
h(x) = 𝑥^2 −4x+ 20

38. À retenir :Manipuler des inéquations
Propriété:
1. On peut ajouter ou soustraire un même nombre à chaque membre
d’une inégalité
2. On peut ajouter membre à membre deux inégalités de même sens
3. On peut multiplier ou diviser chaque membre d’une inégalité par un
même nombre non nul
a) Sans changer le sens de l’inégalité si ce nombre est positif
b) En changeant le sens de l’inégalité si ce nombre est négatif
Exemples:
1. De 2a < b-1 , on déduit 2a + 1 < b , en ajoutant 1 à chaque
membre
2. De a < b et c < 2, on déduit a + c < b + 2
3. De 3 < π, on déduit:
a) 6 < 2π en multipliant par 2, positif
b) -9 > -3π en multipliant par -3, négatif, donc en
changeant le sens de l’inégalité