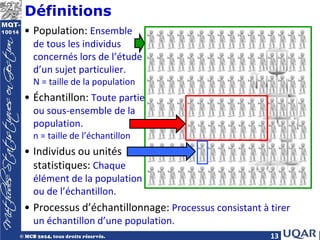
Le document traite des modèles probabilistes, abordant les variables aléatoires, leurs types, et les fonctions de probabilité. Il couvre les concepts de variables aléatoires discrètes et continues, ainsi que les distributions hypergéométriques, binomiales et de Poisson. Il inclut également des exemples, des applications et des exercices pour illustrer ces notions.

1. Modèles probabilistes
C H A P I T R E 4

2. 2
Plan
• Introduction
• Variables aléatoires (v.a.)
– Définition
– Types
• Variables aléatoires discrètes (v.a.d.)
– Fonctions de probabilité et de répartition
– Mesures caractéristiques d’une variable aléatoire
– Distribution
Lecture
• Chapitre 4
Exercices
• Exercices d’application: À faire: #4.1 à 4.14, 4.20 à 4.34
• Vrai ou faux: À faire: #1 à 11, 18, 19, 22 à 28
• Choix multiples et autres exercices: À faire: #29 à 32, 34, 35

3. 3
Introduction
• Dans une expérience aléatoire, il arrive souvent que
l’observateur s’intéresse moins au résultat obtenu qu’à un
nombre associé à ce résultat.
• Exemple #1
– Soit l’expérience aléatoire consistant à choisir 3 personnes
dans le département des ressources humaines et à observer la
suite de bilingues (B) ou d’unilingues français (F) obtenues.
S = {(F, F, F), (F, F, B), (F, B, F), (B, F, F), (F, B, B), (B, F, B),
(B, B, F), (B, B, B)}
– Au lieu de s’intéresser à chacun de ces résultats, on
s’intéresse, par exemple, à la caractéristique numérique
associée à ces résultats soit le nombre de bilingues obtenus.

4. 4
Variables aléatoires (v.a.)
• Définition
– Fonction qui associe à chaque résultat d’une expérience
aléatoire un nombre réel.
– Ensemble des réalisations (ou des résultats) de X sera désigné.
Ex : X = {0, 1, 2, 3}
– On utilise pour représenter une variable aléatoire: une lettre
majuscule.
• Exemple #1:
S X : Nombre de
bilingues obtenus
(B, B, B)
(B, B, F)
(B, F, B)
(F, B, B)
(F, F, F)
(F, F, B)
(F, B, F)
(B, F, F)
0
1
2
3
Ensemble fondamental
Valeurs numériques
possibles de la
variable aléatoire

5. 5
Variables aléatoires (v.a.):
2 types
• Variable aléatoire discrète (v.a.d.)
– Lorsque l’ensemble des réalisations est un ensemble fini ou
infini dénombrable.
Exemples
• Nombre de ventes réalisée suite à la sollicitation de 10 clients
(fini) X = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
• Nombre d’appel téléphonique au service à la clientèle entre midi
et minuit (infini dénombrable) X = {0, 1, 2, 3, 4, 5, 6, …}
• Variable aléatoire continue (v.a.c.)
– Lorsque l’ensemble des résultats est un intervalle de nombres
réels.
Exemples
• Niveau de service atteint pendant une journée, nombre moyen
de clients en attente au dépanneur, rendement d’une ligne de
production d’une usine, temps moyen de service des clients à la
banque, etc.

6. 6
Variables aléatoires (v.a.): Traitement d’une
variable aléatoire discrète
• Fonction de probabilité ou fonction masse de probabilité
ou loi de probabilité
– Définir la fonction de probabilité d’une v.a.d, c’est
associer à chacune des valeurs possibles de la v.a. la
probabilité qui lui correspond.
– Fonction de probabilité:
• Exemple #1
– Soit l’expérience aléatoire consistant à choisir 3 personnes
dans le département des ressources humaines et à observer la
suite de bilingues (B) ou d’unilingues français (F) obtenus.
– L’ensemble des réalisations est : X = {0, 1, 2, 3}
– Il faut maintenant calculer la probabilité associée à chacun de
ces résultats.
( ) ( )
f x P X x
= =

7. 7
V.A.D. Fonctions de probabilité:
Exemple #1
• Solution
– Distribution de probabilité
– Représentation
graphique 
xi 0 1 2 3 4
1
8
3
8
3
8
1
8
0
8
( ) ( )
i i
f x P x
= =
X
3 résultats favorables : (B,F,F) ; (F,B,F) ; (F,F,B)
8 résultats possibles
0
0,1
0,2
0,3
0,4
0 1 2 3
Probabilité
Nombre de personnes bilingues parmi 3
Fonction de masse

8. 8
V.A.D. Fonctions de probabilité
• Propriétés d’une fonction de probabilité


V.A.D. Fonctions de répartition
• La fonction de répartition est une fonction de
probabilités cumulées des valeurs de X jusqu’à xi.
F(xi) = P(X ≤ xi ) = f(x1) + f(x2) +…+ f(xi)
= P(X = x1) + P(X = x2) +...+ P(X = xi)
• C’est la probabilité que la variable aléatoire prenne
une valeur inférieure ou égale à xi.
( )
( )
0,
1
i i
i
f x x
f x
≥ ∀ ∈
=
∑


9. 9
V.A.D. Fonctions de répartition:
Exemple #1
• Solution
– Représentation
graphique 
xi 0 1 2 3 4
1
8
3
8
3
8
1
8
0
8
1
8
4
8
7
8
8
8
8
8
( ) ( )
i i
f x P x
= =
X
( ) ( )
i i
F x P x
= ≤
X
Fonction de probabilité
Fonction de répartition

10. 10
V.A.D. Fonctions de répartition
• Propriétés de la fonction de répartition

 •
 F(x) est non-décroissante, i.e. si x1 < x2, alors F(x1)≤ F(x2)
 Une fonction de répartition = constante entre 2 résultats
 P(a < X ≤ b) = F(b) – F(a)
– Exemple #2: Pour la fonction de répartition suivante:
o P(X ≤ 7)
o P(3 < X ≤ 6)
o P(4 ≤ X < 9)
( )
( ) ( )
0 1
0
lim
i
x
F x
F F x
→−∞
≤ ≤
−∞
= =
1/36
3/36
6/36
10/36
15/36
21/36
26/36
30/36
33/36
35/36
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
1 2 3 4 5 6 7 8 9 10 11 12 13
( ) ( ) 1
lim
x
F F x
→∞+
∞ +
= =

11. 11
V.A.D. Mesures caractéristiques
d’une variable aléatoire
• Espérance mathématique
– Caractérise la tendance centrale (ou la position) de l’ensemble
des valeurs possibles d’une variable aléatoire.
– Notation : E[X] ou µ
– Lorsque X est une v.a. discrète :
E[X] = Σ xi f(xi) = x1f(x1) + x2f(x2) + … + xnf(xn)
• Mode
– xi où f(xi) = P(X = xi) est le plus grand
• Exemple #1: Espérance mathématique?
Mode?
xi 0 1 2 3 4
1
8
3
8
3
8
1
8
0
8
0
0,1
0,2
0,3
0,4
0 1 2 3
Probabilité
Nombre de personnes bilingues parmi 3
Fonction de masse
( ) ( )
i i
f x P x
= =
X

12. 12
V.A.D. Mesures caractéristiques
d’une variable aléatoire
• Variance: Indicateur de l’étalement des valeurs de la variable
aléatoire par rapport à µ
• Écart type (déviation standard):
• Coefficient de variation:
• Exemple #1: Variance?
( ) ( ) ( )
( ) ( ) ( ) ( )
2 2
2
1
2 2
2 2
1
( )
n
i i
i
n
i i
i
Var X E X x f x
x f x E X E X E X
σ µ µ
=
=
 
= = − = − ⋅
 
= ⋅ − = −
   
   
∑
∑
( )
Var X
σ =
% 100
( )
x
CV
E X
σ
= ×
xi 0 1 2 3 4
1
8
3
8
3
8
1
8
0
8
( ) ( )
i i
f x P x
= =
X

13. 13
Définitions
• Population: Ensemble
de tous les individus
concernés lors de l’étude
d’un sujet particulier.
N = taille de la population
• Échantillon: Toute partie
ou sous-ensemble de la
population.
n = taille de l’échantillon
• Individus ou unités
statistiques: Chaque
élément de la population
ou de l’échantillon.
• Processus d’échantillonnage: Processus consistant à tirer
un échantillon d’une population.

14. 14
V.A.D. Distribution
hypergéométrique
• Processus d’échantillonnage
– Plan d’échantillonnage Aléatoire Simple et Sans Remise
(A.S.S.R)
• Notation
o N = taille de la population
o n = taille de l’échantillon
o R = nombre d’individus dans la population qui possède la
caractéristique étudiée
o p = proportion d’individus dans la population qui possède la
caractéristique étudiée = R/N
• Exemple #3:

15. 15
V.A.D. Distribution
hypergéométrique
• Principe
– Si une variable aléatoire X représente le nombre d’individus
dans l’échantillon qui possède la caractéristique étudiée, alors
X obéit à une distribution hypergéométrique.
X ∈ Hg (N, n, p)
(X suit une loi hypergéométrique de paramètres N, n, p)
• Définition mathématique
où a = Np = R p = R/N 0 ≤ p ≤ 1
b = Nq q = 1 – p
– Si X est une v.a. hypergéométrique, alors
• Dans Excel: LOI.HYPERGEOMETRIQUE(x = Succès_échantillon; n = Nombre_échantillon;
R = Succès_population; N = Nombre_population)
.
( )
a b
x n x
N
n
C C
P X x
C
−
= =
( ) ( )
1
N n
E X n p VAR X n p q
N
−
 
= ⋅ = ⋅ ⋅ ⋅ 
−
 

16. 16
V.A.D. Distribution
hypergéométrique: Exemple #3
• Considérons un groupe de 10 personnes dont 2 n’ont pas une
formation en service à la clientèle. On tire au hasard sans
replacement quatre personnes dans le groupe. On considère la v.a.
X donnant le nombre de personnes n’ayant pas la formation en
service à la clientèle dans l’échantillon de 4 personnes.
a) Quelle est la probabilité de trouver aucune personne n’ayant pas la
formation dans l’échantillon?
b) Quelle est la probabilité de trouver 1 personne n’ayant pas la
formation ou moins dans l’échantillon?
c) Quelle est la variance de l’échantillon?

17. 17
V.A.D. Distribution binomiale
• Épreuve de Bernoulli
– Expérience aléatoire simple dont
l’ensemble fondamental se compose de
seulement 2 événements simples
(succès, échec).
• Processus de Bernoulli
– Expérience aléatoire constituée d’une suite d’épreuves de
Bernoulli indépendantes où chaque épreuve ne peut conduire
qu’aux 2 mêmes résultats possibles (succès, échec) et où
chacun de ces résultats à la même probabilité de réalisation
d’une épreuve à l’autre.
• Exemple #3 (modifié): À tour de rôle et de façon
confidentielle, 5 personnes choisissent 1 personne
du groupe.
http://fr.wikipedia.org/wiki/Jacob_Bernoulli
Jacques Bernoulli
(1654-1705)

18. 18
V.A.D. Distribution binomiale
• Notation
o n = nombre d’épreuves de Bernouilli
o p = probabilité de succès
• Principe
– Si une variable aléatoire X représente le nombre de succès
lorsqu’on effectue n épreuves de Bernoulli, alors X obéit à une
distribution binomiale.
X ∈ Bin (n, p)
(X obéit à une loi binomiale de paramètres n, p)
• Définition mathématique
où 0 ≤ p ≤ 1 et q = 1 – p
– Si X est une v.a. binomiale alors
( ) i i
i
x n x
n
i x
P X x C p q −
= = ⋅ ⋅
( ) ( )
E X n p VAR X n p q
= ⋅ = ⋅ ⋅

19. 19
V.A.D. Distribution binomiale:
Exemple #4
• À la fin de sa formation en service à la clientèle, une personne doit
passer un examen objectif comportant 10 questions. Pour chacune
des questions une seule réponse est bonne parmi les 4 réponses
suggérées. Si cette personne répond aléatoirement aux questions:
a) Combien de bonnes réponses peut-elle espérer?
b) Quelle est la probabilité qu’elle réussisse son examen, c’est-à-dire
qu’elle ait au moins 6 bonnes réponses?

20. 20
V.A.D. Distribution binomiale:
Table A1
• Ex: Si X~Bin(n=5, p=0,03), quelle est la valeur de P(X = 0)?
• Dans Excel: LOI.BINOMIALE(x = nombre_succès; n = tirages; p = probabilité_succès;
cumulative 1-vrai, 0-faux)
o P(X = 0) = LOI.BINOMIALE(0;5;0,03;FAUX)= 0,86
o P(X ≤ 1) = P(X=0)+P(X=1) = LOI.BINOMIALE(1;5;0,03;VRAI)= 0,99

21. 21
V.A.D. Loi de Poisson
(distribution de poisson, distribution des
événements rares)
• Principe
– Si une v.a. X représente le nombre de succès
dans un intervalle de temps considéré, alors
X obéit à une distribution de Poisson.
X ∈ Po (λ)
(X suit une loi de Poisson de paramètre λ)
• Notation
o t = période de temps considérée
o α = nombre moyen de succès pour une période de temps
unitaire
o λ = nombre moyen de succès pour la période de temps t
λ = α·t
o ex = fonction exponentiel (sur la calculatrice)
Siméon Denis
Poisson
(1781-1840)
http://fr.wikipedia.org/wiki/Sim
%C3%A9on_Denis_Poisson

22. 22
V.A.D. Loi de Poisson
• Définition mathématique
où x prend une valeur entière
– Si X est une v.a. de Poisson alors
• Exemple #5: Pendant une semaine de vacances, un seul guichet
est ouvert à la Banque Soldi. Les clients arrivent à un taux moyen
de 6 clients à l’heure. Pendant une période de 2 heures données,
a) Quelle est la probabilité que se présentent à ce guichet exactement
8 clients?
b) Quel est le nombre espéré de clients pour une période de 2 heures?
( )
!
x
e
P X x
x
λ
λ
−
⋅
= =
( ) ( )
E X VAR X
λ λ
=

23. 23
V.A.D. Loi de Poisson: Table A2
• Ex: Si X~Po (λ=0,4), quelle est la valeur de P(X = 0)?
• Dans Excel: LOI.POISSON(x=nombre_succès; λ=probabilité_succès; cumulative 1-vrai,
0-faux)
o P(X = 0) = LOI.POISSON(0;0,4;FAUX)= 0,6703
o P(X ≤ 1)= P(X=0)+P(X=1) = LOI.POISSON(1;0,4;VRAI)= 0,9384

24. 24
V.A.D. Loi de Poisson
• Particularité
– La distribution de poisson peut être utilisée comme
approximation de la distribution binomiale.
X ∈ Bi (n, p) ≅ X ∈ Po(λ = np)
– En général l’approximation est valable si:
• n > 20, p ≤ 0,1 et np ≤ 5
• Exemple #4 (modifié): La personne doit passer un examen objectif
comportant 50 questions. Pour chacune des questions, une seule
réponse est bonne parmi les 10 réponses suggérées. Si cette
personne répond aléatoirement aux questions, quelle est la
probabilité qu’elle ait exactement 7 bonnes réponses?

25. 25
V.A.D. Exemple récapitulatif #1
• Pour célébrer son 150e anniversaire, un magasin organise un tirage:
– Chaque client, immédiatement après avoir payé ses achats,
prend un jeton dans un sac contenant 100 jetons du nom du
magasin et 900 jetons blancs.
– Si le client tire un jeton du nom du magasin, on lui remet un
chèque d’un montant égal à 30% de ses achats;
– Si le client tire un jeton blanc, on l’encourage à revenir au
magasin et à retenter sa chance.
– Après que le client ait validé son jeton, il est immédiatement
remis dans le sac de tirage.
• Quelle est la probabilité pour que, dans un groupe de 8 clients, il y
ait 4 gagnants?

26. 26
V.A.D. Exemple récapitulatif #2
• Pour faire la vérification de 40 comptes-clients, 5 personnes sont
désignées. Vous savez, avant même de commencer le travail, que
10 comptes clients sont incorrects. Vous vous divisez le travail
équitablement.
a) Quel est le nombre moyen de comptes-clients incorrects auquel un
vérificateur doit s’attendre?
b) Quelle est la probabilité que l’un des vérificateurs trouve
exactement 5 comptes-clients incorrects?

27. 27
Références
• Baillargeon G. (2020) Méthodes statistiques en gestion,
Éditions SMG.
• Bouchard J. (2011) Notes de cours MQT-1102, Université
Laval.