Cours de probabilités chap2.pptx

GHIZLAN LOUMRHARI
S E P T E M B R E 2 0 1 9
Cours de probabilités

Chapitre 2. Variables aléatoires
L’espérance mathématique et la variance
Caractéristiques :
Les deux principales caractéristiques, la moyenne et la variance, d’une
variables aléatoire discrètes sont données par



n
i
i
i p
x
X
E
1
)
(
 
 

n
i
i
i X
E
x
p
X
V
2
)
(
)
(

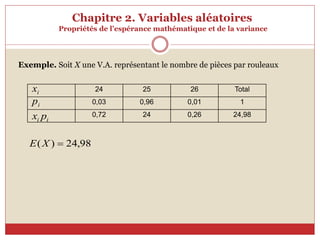
L’espérance mathématique
L’espérance mathématique E(X) d’une variable aléatoire X
joue le rôle dévolu à la moyenne en statistiques : elle correspond à
la valeur moyenne espérée par un observateur lors d’une réalisation
de la variable aléatoire X. On a :
lorsque X peut prendre N valeurs différentes x1; ….. ; xn avec
comme probabilités élémentaires pi = P[X = xi ].

La variance
Pour décrire plus précisément le comportement de X, sans pour
autant caractériser complètement la loi de X, on peut s’intéresser
aux écarts de X par rapport à cette moyenne.
Cependant, si on considère simplement la différence X-E(X),
on obtient un écart moyen E(X-E(X))=0 (par linéarité de
l’espérance). On pourrait considérer la valeur moyenne de
|X-E(X)| mais on préfère considérer la moyenne de
plus pertinente mathématiquement.

La variance
La variance mesure ainsi la déviation moyenne autour de la
moyenne espérée E(X), et est définie par :
Elle est toujours positive puisqu’il s’agit de l’espérance d’un carré.
Autre expression de la variance :  2
2
)
(
)
(
)
( X
E
X
E
X
V 


L’Ecart-type
Pour mesurer la dispersion d’une variable aléatoire X, on considère
souvent en statistiques l’écart-type, lié à la variance par :

Propriétés de l’espérance mathématique et de la variance
Propriété de la moyenne
a
a
E 
)
(
)
(
)
( X
aE
aX
E 
)
(
)
(
)
( Y
E
X
E
Y
X
E 


)
(
)
(
)
( Y
E
X
E
XY
E 
 si X et Y sont indépendantes

Propriété de la variance
si X et Y sont indépendantes
0
)
( 
a
V
)
(
)
( 2
X
V
a
aX
V 
)
(
)
(
)
( Y
V
X
V
Y
X
V 


0
)
( 
X
V
 2
2
)
(
)
(
)
( X
E
X
E
X
V 


L’espérance mathématique et de la variance
Exemple. Une banque accepte de ses clients des rouleaux de pièces de 10
MAD sans en contrôler le nombre (en principe 25 pièces). On suppose que 3%
des rouleaux contiennent seulement 24 pièces, que 96% des rouleaux
contiennent 25 pièces et que 1% des rouleaux contiennent 26 pièces.
Si on note X la V.A. qui représente le nombre de pièces d’un
rouleaux calculez E(X) et V(X)

Exemple. Soit X une V.A. représentant le nombre de pièces par rouleaux
24 25 26 Total
0,03 0,96 0,01 1
0,72 24 0,26 24,98
i
x
i
p
i
i p
x
98
,
24
)
( 
X
E

X est une variable aléatoire de moyenne 24,98 et de variance
0,0396 (ou d’écart-type 0,199)
24 25 26 Total
0,03 0,96 0,01 1
0,72 24 0,26 24,98
576 625 676
17,28 600 6,76 624,04
i
x
i
p
i
i p
x
2
i
x
i
i p
x2
98
,
24
)
( 
X
E 04
,
624
)
( 2

X
E
0396
,
0
)
(
)
(
)
( 2
2


 X
E
X
E
X
V

Les lois de probabilité paramétriques
 Les lois paramétriques sont des lois de probabilité qui dépendent d’un ou de
plusieurs paramètres (généralement 1 ou 2).
 Des phénomènes aléatoires très différents peuvent être décrits par une
même loi avec des valeurs différentes pour les différents paramètres.
 Ainsi un nombre limité de lois permettent de décrire pratiquement une
infinité de phénomènes aléatoires.

Les lois discrètes. Loi de Bernoulli
X suit une loi de Bernoulli de paramètre p notée B(p) si elle prend les valeurs 0
et 1 avec les probabilités P(X = 1) = p et P(X=0) = 1- p :
Propriétés : et
Domaine d’application : Un seul tirage (sans remise)
k
k
p
p
k
X
P 


 1
)
1
(
)
(
p
X
E 
)
( )
1
(
)
( p
p
X
V 


Exemple. On lance une pièce de monnaie, et on choisit Pile comme succès.
Calculer l’espérance et la variance de X
X peut prendre soit 1 soit 0
Pile = succès =1
Face =échec =0
Face Pile
X 0 1
P(X=xi) 0,5 0,5
E(X)=p=0,5
V(X)=p(1-P)=0,5.0,5=0,25

Exemple. On lance un dé, et on choisit que le succès est d’avoir un 6
X peut prendre soit 1 soit 0
« 6 » = succès =1
« 1,2,3,4,5 » =échec =0 1,2,3,4,5 6
X 0 1
P(X=xi) 5/6=0,83 1/6=0,16
E(X)=p=0,16
V(X)=p(1-P)=1/6.5/6=0,138

Les lois discrètes. Loi Binomiale
X suit une loi Binomiale de paramètres n et p, notée B(n,p) si elle prend les
valeurs 0,1,2,…,n avec les probabilités :
Propriétés : et
Domaine d’application : Dualité (urnes contenant boules blanches et
boules noires) avec remise.
k
n
k
k
n p
p
C
k
X
P 


 )
1
(
)
(
np
X
E 
)
( )
1
(
)
( p
np
X
V 


Les lois discrètes. Loi Binomiale
Exemple. La probabilité d’obtenir exactement 2 faces au cours de 6 lancers
d’une pièce de monnaie
k
n
k
k
n p
p
C
k
X
P 


 )
1
(
)
(

Les lois discrètes. Loi géométrique
X suit une loi géométrique de paramètre p notée G(p,k) si sa distribution est
donnée par
Propriétés : et
Domaine d’application : C’est la loi du temps d’attente du premier succès
dans les épreuves de Bernoulli répétées ou dans un tirage avec remise.
Exemple. Nombre de tirage nécessaire pour obtenir pile lors du lancement
d’une pièce
1
)
1
(
)
( 


 k
p
p
k
X
P
p
X
E /
1
)
(  2
/
)
1
(
)
( p
p
X
V 


Les lois discrètes. Loi géométrique
Exemple. un lot de 50 pièces, dont 20 sont de type A, on choisit
avec remise une pièce type A. Quelle est la probabilité de sortir une
pièce de type A pour la première fois après le 5eme tirage?

Les lois discrètes. Loi de poisson
X suit une loi de Poisson de paramètre notée
si sa distribution est donnée par
Propriétés : et
Domaine d’application : Cette loi s’applique au comportement du nombre
d’évènements se produisant dans un laps de temps fixe (ou intervalles
spatiaux).
 )
(
P
,...
2
,
1
,
0
!
)
( 



x
x
e
x
X
P
x




)
(X
E 

)
(X
V

Les variables aléatoires continues
La v.a. continue. La v.a. est dite continue si ses réalisations sont
n’importe quels réels dans un intervalle donné (le montant des
transactions pendant une journée à la BVC). Elle est caractérisée par
cet ensemble et la probabilité d’apparition appelée distribution ou loi de
probabilité et prend la forme d’une expression analytique appelée
densité.
Caractéristiques :
Les deux principales caractéristiques, la moyenne et la variance, d’une
variables aléatoire continues sont données par
 










 dx
x
f
X
E
x
X
V
dx
x
xf
X
E )
(
)
(
)
(
)
(
)
(
2

Exemple. On considère la fonction f définie sur par
et X est une variable aléatoire de densité f.
Calculer les probabilités suivantes :
a.
b.

a.
a b
f(x)

b.
3
A1 + A2 =1
f(x)
A2 =1 - A1

Les lois continues. La loi normale
La loi normale : X suit une loi Normale de paramètres μ et σ notée si sa
densité est donnée par :
2
2
1
2
1
)
,
;
(





 

 





x
e
x
f
Propriétés : et


)
(X
E 2
)
( 

X
V

Les lois continues. La loi normale
μ
- Il existe une infinité des lois normales
- La loi n’est pas tabulée. Problème
- Il faut la standardiser

Les lois continues. La loi normale centrée réduite
La loi normale centrée réduite (standard) : Si on pose on
obtient une V.A. noté N(0,1) de densité
Propriétés : et




X
Z
2
2
2
1
)
(
z
e
z
f



0
)
( 
X
E 1
)
( 
X
V

0

Exemple.
Calculer :
)
20
,
500
( 2
N
X 
)
540
460
(
)
540
(
)
520
(




X
P
X
P
X
P

Exemple. Soit X une v.a continue suit une loi normale ( , ). Déterminer
Tel que

Les lois continues. Khi-deux
Loi de Khi-deux (chi-deux). La V.A. X suit une loi de Khi-deux de paramètre n,
notée si elle est donnée par
sont n variables aléatoires normales standards
indépendantes et n est appelé n.d.d.l (nombre de degrés de libertés)
Propriétés : et
)
(
2
n




n
i
i
Y
X
1
2
)
,...,
2
,
1
( n
i
Yi 
0
)
( 
X
E 1
)
( 
X
V



n
i
i
Y
X
1
2

Cette loi est bien entendu, tabulée

Exemple. Considérons une variable aléatoire X de loi
Pour n=13,
(i) Calculer P(5<X<24,73)
(ii) Déterminer les valeurs a et b si : P(X<a)=0,99 et P(X>b)=0,95
)
(
2
n


Corrigé.
1. Pour n=13,
(i) Calculer P(5<X<24,73)

Corrigé.
(ii) Déterminer les valeurs a et b si P(X<a)=0,99 et P(X>b)=0,95
P(X<a)=0,99 D’après la table de Khi deux a=27,68
D’après la table de Khi deux b=0,89

Les lois continues. Loi de Student
Loi de Student. La V.A. X suit une loi de Student de paramètre n, notée
si elle est donnée par
X et Y sont indépendantes
Propriétés : et
0
)
( 
X
E
2
)
(


n
n
X
V
)
(n
t
n
Z
Y
X 
)
1
,
0
(
N
X 
2
n
Y 


0

Exemple. Soit X est une variable aléatoire qui suit une loi de student de
v= 10 degré de liberté. En utilisant une table donnant la fonction de
répétition de la loi de student,
1. Calculer les probabilités suivantes : P(X<-1,093)
2. déterminer a et b dans les cas suivantes : P(X<a)=0,9 et

Corrigé.
1. Calculer les probabilités suivantes : P(X<-1,093) et P(0,541<X<2,228)

Les lois continues. Le théorème central limite
Le théorème central limite
Soit X1, X2, … une suite de variables aléatoires réelles définies sur le même espace
de probabilité, indépendantes et identiquement distribuées suivant la même loi L.
Supposons que l‘espérance μ et l’écart-type σ de L existent et soient finis avec
σ ≠ 0.
Considérons la somme
Si n est grand alors est une variable aléatoire normale de moyenne n μ et de
variance
n
n X
X
X
S ,...,
, 2
1

n
S
2

n

Exemple 1. Une banque accepte de ses clients des rouleaux de pièces
de 10 MAD sans en contrôler le nombre (en principe 25 pièces). On
suppose que 3% des rouleaux contiennent seulement 24 pièces, que
96% des rouleaux contiennent 25 pièces et que 1% des rouleaux
contiennent 26 pièces.
(i) Si on note X la V.A. qui représente le nombre de pièces d’un
rouleaux calculez E(X) et V(X)
(ii) Calculez les probabilités pour que 400 rouleaux contiennent
- Moins de 10 000 pièces
- Moins de 9 990 pièces

X est une variable aléatoire de moyenne 24,98 et de variance
0,0396 (ou d’écart-type 0,199)
24 25 26 Total
0,03 0,96 0,01 1
0,72 24 0,26 24,98
576 625 676
17,28 600 6,76 624,04
i
x
i
p
i
i p
x
2
i
x
i
i p
x2
98
,
24
)
( 
X
E 04
,
624
)
( 2

X
E
0396
,
0
)
(
)
(
)
( 2
2


 X
E
X
E
X
V




400
1
i
i
n X
S
?
)
10000
( 

n
S
P
n
S
(ii) On définit la V.A.
Et on cherche
Mais on ne connait pas la loi suivie par la variable aléatoire

(ii) X n’est pas normale mais comme n est grand (400 > 30), le TCL
s ’applique
La nouvelle variable aléatoire normale de paramètres

n
X
S
E
i
i 
 

400
1
400)
(



400
1
i
i
n X
S
2
400
1
400 )
(
)
( 
n
X
V
S
V
i
i 
 


L’utilisation du TCL montre que
Définissons la variable aléatoire normale centrée et
réduite
)
1
,
0
(
N
n
n
S
Z n
n 




)
,
( 2

 n
n
N
Sn 






 







 




n
n
Z
P
n
n
n
n
S
P
S
P n
n
n





 10000
10000
)
10000
(
 
01
,
2
400
199
,
0
98
,
24
400
10000
)
10000
( 














 n
n
n Z
P
Z
P
S
P
97778
,
0
)
10000
( 

n
S
P
La probabilité pour que 400 rouleaux contiennent moins de 10 000
pièces






 







 




n
n
Z
P
n
n
n
n
S
P
S
P n
n
n





 9990
9990
)
9990
(
 
5025
,
0
400
199
,
0
98
,
24
400
9990
)
9990
( 















 n
n
n Z
P
Z
P
S
P
)
5025
,
0
(
1
)
9990
( 


 n
n Z
P
S
P
La probabilité pour que 400 rouleaux contiennent moins de 9 990
pièces
3077
,
0
6923
,
0
1
)
9990
( 



n
S
P

Cours de probabilités chap2.pptx

Contenu connexe

Tendances

Similaire à Cours de probabilités chap2.pptx

Cours de probabilités chap2.pptx