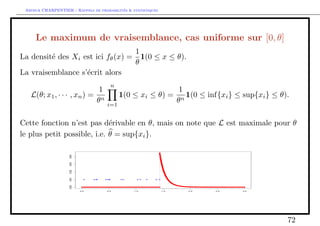
Le document présente des rappels sur les probabilités et statistiques, abordant des concepts tels que la modélisation statistique, l'estimation et les théorèmes limites, notamment la loi des grands nombres et le théorème central limite. Des méthodes d'estimation et de variabilité ainsi que des propriétés asymptotiques des statistiques à partir d'échantillons aléatoires sont également discutées. Enfin, il est fait mention des intervalles de confiance et de leurs implications statistiques.

1. Arthur CHARPENTIER - Rappels de probabilites statistiques
Probabilites statistiques
quelques brefs rappels # 2
Arthur Charpentier, 2014
http ://freakonometrics.hypotheses.org/category/courses/m1-statistique
1

2. Arthur CHARPENTIER - Rappels de probabilites statistiques
Plan du cours
Introduction, la modelation statistique
Rappels de probabilite
Fonctions usuelles, P, F, f, E, Var
Lois uselles, discetes et continues
Conditionnement, esperance conditionnelle et melanges
Convergence, approximations et theoremes limites
Loi(s) des grands nombres
Theoreme central limite
Rappels de statistique (mathematique)
De la statistique descriptive a la statistique mathematique
Echantillonnage, moyenne et variance
Intervalle de con

3. ance
Introduction aux tests
2

4. Arthur CHARPENTIER - Rappels de probabilites statistiques
L'estimateur comme variable aleatoire
En statistique descriptive, on construit des estimateurs comme des fonctions des
valeurs de l'echantillon, fx1; ; xng, e.g.
xn =
x1 + + xn
n
En statistique mathematique, on suppose que xi = Xi(!), i.e. la realisation d'un
variable aleatoire sous-jacente
Xn =
X1 + + Xn
n
X1,..., Xn etant des variables aleatoires, Xn devient une variable aleatoire.
Exemple : supposons que nous disposons d'un echantillon de n = 20 valeurs
tirees suivant une loi uniforme sur [0; 1].
3

5. Arthur CHARPENTIER - Rappels de probabilites statistiques
Distribution de la moyenne d'un échantillon U([0,1])
Fréquence
0.0 0.2 0.4 0.6 0.8 1.0
0 50 100 150 200 250 300
0.457675
l
Figure 1 { Distribution de la moyenne de fX1; ;X10g, Xi U([0; 1]).
4

6. Arthur CHARPENTIER - Rappels de probabilites statistiques
Distribution de la moyenne d'un échantillon U([0,1])
Fréquence
0.0 0.2 0.4 0.6 0.8 1.0
0 50 100 150 200 250 300
0.567145
l l l l l l l ll l l l l l l l ll l l l l l l l l l l l l l l l l l l l ll l l l l l ll l l l l l l l l l l l l ll l lll l l l l l l l l ll ll l l ll l l l ll l l l l l lll ll ll l l ll l l l l l
lll l ll l ll ll ll ll l l l l l lll ll l l ll ll l l ll l l l l ll ll l l ll l ll l l l l ll lll l l l l l ll l l l l ll l lll lll ll ll l l Figure 2 { Distribution de la moyenne de fX1; ;X10g, Xi U([0; 1]).
5

7. Arthur CHARPENTIER - Rappels de probabilites statistiques
L'estimateur comme variable aleatoire
Si l'echantillon change, l'estimateur n'est pas le m^eme.
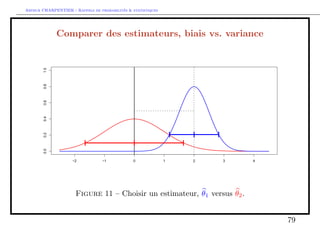
Constituons 1000 echantillons de maniere aleatoire. En moyenne, l'estimateur
vaut 1=2. Aussi, la moyenne empirique est un estimateur sans biais de 1=2,
l'esperance mathematique de la loi uniforme sur [0; 1].
Cet estimateur a une variance, et aussi une loi (en l'occurence une densite). Ici,
la moyenne empirique suit (presque) une loi normale.
On distingera toutefois les comportements a distance

8. nie (n

9. xe) et
asymptotique (theoremes limites - loi des grands nombres et theoreme central
limite - obtenus lorsque n ! 1).
6

10. Arthur CHARPENTIER - Rappels de probabilites statistiques
Petites proprietes preliminaires
Soit x = (x1; ; xn) 2 Rn. Posons x =
x1 + + xn
n
. Alors,
min
m2R
(
Xn
i=1
[xi m]2
)
=
Xn
i=1
[xi x]2
et
Xn
i=1
[xi x]2 =
Xn
i=1
x2i
nx2
7

11. Arthur CHARPENTIER - Rappels de probabilites statistiques
La moyenne (empirique)
De

12. nition 1. Soit fX1; ;Xng des variables i.i.d. de loi F. La moyenne
empirique est
Xn =
X1 + + Xn
n
=
1
n
Xn
i=1
Xi
Si on suppose les Xi d'esperance

13. nie (notee ), alors
E(Xn) = E
1
n
Xn
i=1
Xi
!
=
1
n
Xn
i=1
E(Xi) =
1
n
n =
par linearite de l'esperance
Proposition 2. Si on suppose les Xi d'esperance

14. nie (notee ),
E(Xn) = :
La moyenne est un estimateur sans biais de l'esperance mathematique.
8

15. Arthur CHARPENTIER - Rappels de probabilites statistiques
La moyenne (empirique)
Si on suppose les Xi independants de variance

16. nie (notee 2), alors
Var(Xn) = Var
1
n
Xn
i=1
Xi
!
=
1
n2
Xn
i=1
Var (Xi) =
1
n2 n2 =
2
n
car les variables sont independantes, et car la variance est quadratique.
Proposition 3. Si on suppose les Xi i.i.d. de variance

17. nie (notee 2),
Var(Xn) =
2
n
:
9

18. Arthur CHARPENTIER - Rappels de probabilites statistiques
La variance (empirique)
De

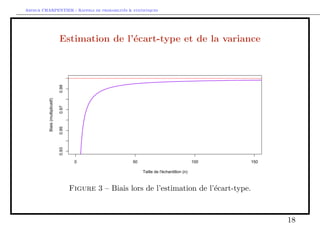
19. nition 4. Soit fX1; ;Xng des variables i.i.d. de loi F. La variance
empirique est
S2n
=
1
n 1
Xn
i=1
[Xi Xn]2:
Si on suppose les Xi de variance

20. nie (notee 2),
E(S2n
) = E
1
n 1
Xn
i=1
[Xi Xn]2
!
=
E
1
n 1
Xn
i=1
X2
i nX
2
n
#!
par la propriete preliminaire enoncee auparavant
E(S2n
) =
1
n 1
[nE(X2
i ) nE(X
2
)]
=
1
n 1
n(2 + 2) n
2
n
+ 2
= 2
car Var(X) = E(X2) E(X)2
10

21. Arthur CHARPENTIER - Rappels de probabilites statistiques
La variance (empirique)
Proposition 5. Si on suppose les Xi independants de variance

22. nie (notee 2),
E(S2n
) = 2:
2n
La variance (empirique) est un estimateur sans biais de la variance.
Remarque Pour avoir un estimateur sans biais, on considere comme estimateur
S, avec un facteur n 1, et non pas
eS2n
=
1
n
Xn
i=1
[Xi Xn]2
(qui reste un estimateur classique).
11

23. Arthur CHARPENTIER - Rappels de probabilites statistiques
Cas d'un echantillon Gaussien
2n
Proposition 6. Si on suppose les Xi i.i.d. de loi N(; 2), alors
Xn et Ssont des variables aleatoires independantes,
Xn a pour loi N
;
2
n
(n 1)S2n
=2 a pour loi 2(n 1).
Remarque Pour comprendre l'histoire du n 1 degres de libertes pour une
somme de n termes, notons que
S2n
=
1
n 1
Xn
i=1
(Xi Xn)2
#
=
1
n 1
(X1 Xn)2 +
Xn
i=2
(Xi Xn)2
#
soit S2n
=
1
n 1
2
4
Xn
i=2
!2
(Xi Xn)
+
Xn
i=2
(Xi Xn)2
3
5
car
Xn
i=1
(Xi Xn) = 0. Aussi S2n
est fonction de n 1 variables (centrees),
X2 Xn; ;Xn Xn
12

24. Arthur CHARPENTIER - Rappels de probabilites statistiques
Cas d'un echantillon Gaussien
Proposition 7. Si on suppose les Xi i.i.d. de loi N(; 2), alors
p
n
Xn
suit une loi N(0; 1)
p
n
Xn
Sn
suit une loi de Student a n 1 degres de liberte
En eet,
p
n
Xn
S
=
p
n
Xn
| {z }
N(0;1)
=
r
(n 1)S2n
2 | {z }
2(n1)
p
n 1
13

25. Arthur CHARPENTIER - Rappels de probabilites statistiques
Proprietes asymptotiques
Proposition 8. Si on suppose les Xi i.i.d. de loi F, de moyenne et de
variance 2 (

26. nie). Alors pour tout 0,
lim
n!1P(jXn j ) = 0
i.e. Xn
P!
(convergence en probabilite).
Proposition 9. Si on suppose les Xi i.i.d. de loi F, de moyenne et de
variance 2 (

27. nie). Alors pour tout 0,
lim
n!1P(jS2n
2j )
Var(S2n
)
2
i.e. une condition susante pour que S2n
P!
2 (convergence en probabilite) est
que Var(S2n
) ! 0 lorsque n ! 1.
14

28. Arthur CHARPENTIER - Rappels de probabilites statistiques
Proprietes asymptotiques
Proposition 10. Si on suppose les Xi i.i.d. de loi F, de moyenne et de
variance 2 (

29. nie). Alors pour tout z 2 R,
lim
n!1P
p
n
Xn
z
=
Z z
1
1
p
2
exp
t2
2
dt
i.e.
p
n
Xn
L!
N(0; 1):
Remarque Si les Xi ont pour loi N(; 2), alors
p
n
Xn
N(0; 1):
15

30. Arthur CHARPENTIER - Rappels de probabilites statistiques
Estimation de la variance
Considerons un echantillon Gaussien, alors
Var
(n 1)S2n
2
= Var(Z) avec Z 2
n1
donc cette quantite vaut
(n 1)2
4 Var(S2n
) = 2(n 1)
de telle sorte que
Var(S2n
) =
2(n 1)4
(n 1)2 =
24
(n 1)
:
16

31. Arthur CHARPENTIER - Rappels de probabilites statistiques
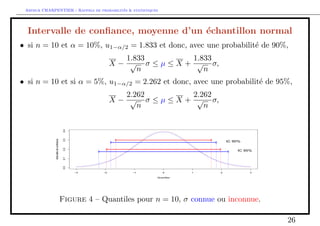
Estimation de l'ecart-type et de la variance
Considerons le cas ou Xi N(; 2). Un estimateur naturel de est
Sn =
p
S2n
=
vuut
1
n 1
Xn
i=1
(Xi Xn)2
On peut alors montrer que
E(Sn) =
r
2
n 1
(n=2)
([n 1]=2)
1
1
4n
7
32n2
6=
mais
Sn
P!
et
p
n(Sn )
L!
N
0;
2
17

32. Arthur CHARPENTIER - Rappels de probabilites statistiques
Estimation de l'ecart-type et de la variance
0 50 100 150
0.93 0.95 0.97 0.99
Taille de l'échantillon (n)
Biais (multiplicatif)
Figure 3 { Biais lors de l'estimation de l'ecart-type.
18

33. Arthur CHARPENTIER - Rappels de probabilites statistiques
Echantillon transforme
Soit g : R ! R susemment reguliere pour ecrire un developpement de Taylor en
tout point,
g(x) = g(x0) + g0(x0) [x x0] + un reste
Soit Yi = g(Xi). Alors, si E(Xi) = avec g0()6= 0
Yi = g(Xi) g() + g0() [Xi ]
de telle sorte que
E(Yi) = E(g(Xi)) g()
et
Var(Yi) = Var(g(Xi)) [g0()]2Var(Xi)
Remarque Il ne s'agit que d'approximations.
19

34. Arthur CHARPENTIER - Rappels de probabilites statistiques
Echantillon transforme
La delta-method permet d'obtenir des proprietes asymptotiques.
Proposition 11. Si on suppose les Xi i.i.d. de loi F, de moyenne et de
variance 2 (

35. nie), alors
p
n(Xn )
L!
N(0; 2)
Et si g0()6= 0, alors
p
n(g(Xn) g())
L!
N(0; [g0()]22)
Proposition 12. Si on suppose les Xi i.i.d. de loi F, de moyenne et de
variance 2 (

36. nie), et si g0() = 0 mais g00()6= 0, alors
p
n(g(Xn) g())
L!
g00()
2
22(1)
20

37. Arthur CHARPENTIER - Rappels de probabilites statistiques
Echantillon transforme
Example Si 6= 0,
p
n
1
Xn
1
L!
N
0;
1
4 2
21

38. Arthur CHARPENTIER - Rappels de probabilites statistiques
Intervalle de con

39. ance pour
Quand on parlera de l'intervalle de con

40. ance de a un niveau de con

41. ance 1
(e.g. 95%), il s'agira du plus petit intervallle I tel que
P( 2 I) = 1 :
Notons u le quantile de la loi N(0; 1) au niveau , i.e.
u=2 = u1=2 veri

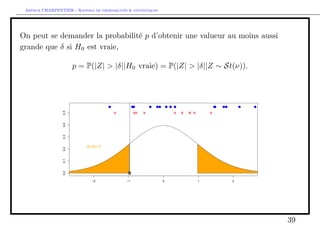
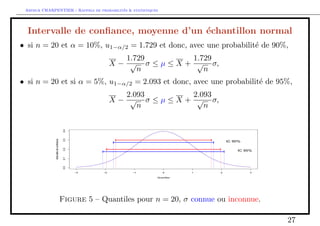
42. e (u=2) = =2
Comme Z =
p
n
Xn
N (0; 1),
on peut en deduire que P(Z 2 [u=2; u1=2]) = 1 ,
et donc
P
2
X +
u=2 p
n
;X +
u1=2 p
n
= 1 :
22

43. Arthur CHARPENTIER - Rappels de probabilites statistiques
Intervalle de con

44. ance, moyenne d'un echantillon normal
si = 10%, u1=2 = 1:64 et donc, avec une probabilite de 90%,
X
1:64
p
n
X +
1:64
p
n
;
si = 5%, u1=2 = 1:96 et donc, avec une probabilite de 95%,
X
1:96
p
n
X +
1:96
p
n
;
23

45. Arthur CHARPENTIER - Rappels de probabilites statistiques
Intervalle de con

46. ance, moyenne d'un echantillon normal
Si la variance est inconnue, on l'estime par S2n
=
1
n 1
Xn
i=1
X2
i
!
X
2
n.
On a vu que
(n 1)S2n
2 =
Xn
i=1
0
BB@
Xi E(X)
| {z }
N(0;1)
1
2
CCA
| {z }
loi du 2(n)
0
BBB@
Xn E(X)
p
| =
{z n }
N(0;1)
1
2
CCCA
| {z }
loi du 2(1)
Le theoreme de Cochrane permet de conclure que
(n 1)S2n
2
2(n 1).
24

47. Arthur CHARPENTIER - Rappels de probabilites statistiques
2n
Intervalle de con

48. ance, moyenne d'un echantillon normal
Comme Xn et Ssont independantes,
T =
p
n 1
Xn
Sn
=
Xn
p
=
q n1
(n1)S2n
(n1)2
St(n 1):
Si t(n1)
=2 designe le quantile de la loi St(n 1) au niveau =2, i.e.
t(n)
=2 = t(n1)
1=2 veri

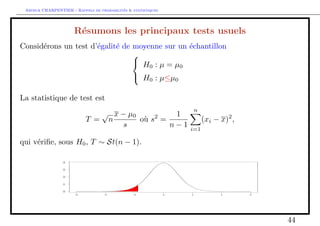
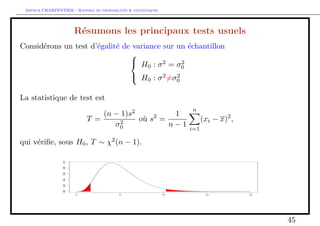
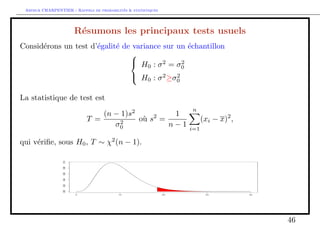
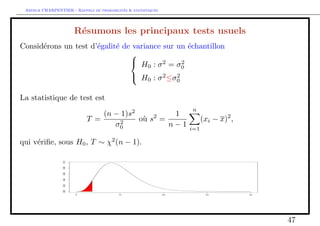
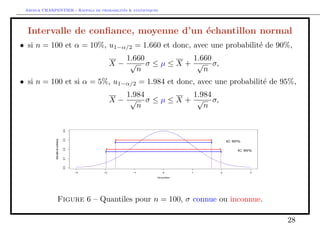
49. e P(T t(n1)
=2 ) = =2
on peut en deduire que P(T 2 [t(n1)
=2 ; t(n1)
1=2]) = 1 , et donc
P
0
@ 2
2
4X +
t(n1)
=2 p
n 1
;X +
t(n1)
1=2 p
n 1
3
5
1
A = 1 :
25

50. Arthur CHARPENTIER - Rappels de probabilites statistiques
Intervalle de con

51. ance, moyenne d'un echantillon normal
si n = 10 et = 10%, u1=2 = 1:833 et donc, avec une probabilite de 90%,
X
1:833
p
n
X +
1:833
p
n
;
si n = 10 et si = 5%, u1=2 = 2:262 et donc, avec une probabilite de 95%,
X
2:262
p
n
X +
2:262
p
n
;
−3 −2 −1 0 1 2 3
0.0 0.1 0.2 0.3 0.4
Quantiles
Intervalle de confiance
IC 90%
IC 95%
Figure 4 { Quantiles pour n = 10, connue ou inconnue.
26

52. Arthur CHARPENTIER - Rappels de probabilites statistiques
Intervalle de con

53. ance, moyenne d'un echantillon normal
si n = 20 et = 10%, u1=2 = 1:729 et donc, avec une probabilite de 90%,
X
1:729
p
n
X +
1:729
p
n
;
si n = 20 et si = 5%, u1=2 = 2:093 et donc, avec une probabilite de 95%,
X
2:093
p
n
X +
2:093
p
n
;
−3 −2 −1 0 1 2 3
0.0 0.1 0.2 0.3 0.4
Quantiles
Intervalle de confiance
IC 90%
IC 95%
Figure 5 { Quantiles pour n = 20, connue ou inconnue.
27

54. Arthur CHARPENTIER - Rappels de probabilites statistiques
Intervalle de con

55. ance, moyenne d'un echantillon normal
si n = 100 et = 10%, u1=2 = 1:660 et donc, avec une probabilite de 90%,
X
1:660
p
n
X +
1:660
p
n
;
si n = 100 et si = 5%, u1=2 = 1:984 et donc, avec une probabilite de 95%,
X
1:984
p
n
X +
1:984
p
n
;
−3 −2 −1 0 1 2 3
0.0 0.1 0.2 0.3 0.4
Quantiles
Intervalle de confiance
IC 90%
IC 95%
Figure 6 { Quantiles pour n = 100, connue ou inconnue.
28

56. Arthur CHARPENTIER - Rappels de probabilites statistiques
La lecture des tables
Fonction de repartition de la loi normale X N(0; 1),
P(X u) = (u) =
Z u
1
1
p
2
ey2=2dy
Example P(X 1; 96) = 0; 975.
29

57. Arthur CHARPENTIER - Rappels de probabilites statistiques
Interpretation d'un intervalle de con

58. ance
Si on genere des echantillons i.i.d. suivant une loi N(; 2), avec et 2

59. xes, il y
a 90 chances sur 100 que soit dans un des intervalles suivants
X +
u=2 p
n
;X +
u1=2 p
n
l
l
l
l
ll
l
l
l
l
l
lll
l
l
ll
l
ll
l
l
ll
l
ll
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
ll
l
l
l
ll
l
l
l
l
ll
l
l
l
ll
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
ll
l
l
l
ll
l
l
l
l
l
l
l
l
l
0 50 100 150 200
−1.0 −0.5 0.0 0.5 1.0
intervalle de confiance Figure 7 { Intervalle de con

60. ance pour , avec 2 connue.
30

61. Arthur CHARPENTIER - Rappels de probabilites statistiques
Interpretation d'un intervalle de con

62. ance
ou 2
4X +
t(n1)
=2 p
n 1
;X +
t(n1)
1=2 p
n 1
3
5
l
l
l
l
ll
l
l
l
l
l
lll
l
l
ll
l
ll
l
l
ll
l
ll
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
ll
l
l
l
ll
l
l
l
l
ll
l
l
l
ll
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
ll
l
l
l
ll
l
l
l
l
l
l
l
l
l
0 50 100 150 200
−1.0 −0.5 0.0 0.5 1.0
intervalle de confiance
Figure 8 { Intervalle de con

63. ance pour , avec 2 estimee.
31

64. Arthur CHARPENTIER - Rappels de probabilites statistiques
Un peu de tests
Le lien entre la decision est la vraie valeur peut ^etre represente par le tableau
ci-dessous
H0 vraie H1 vraie
Decision d0 Bonne decision erreur de seconde espece
Decision d1 erreur de premiere espece Bonne decision
32

65. Arthur CHARPENTIER - Rappels de probabilites statistiques
Resumons les principaux tests usuels
Considerons un test d'egalite de moyenne sur un echantillon
8
:
H0 : = 0
H0 : 6=0
La statistique de test est
T =
p
n
x 0
s
ou s2 =
1
n 1
Xn
i=1
(xi x)2;
qui veri

66. e, sous H0, T St(n 1).
−6 −4 −2 0 2 4 6
0.0 0.1 0.2 0.3 0.4
33

67. Arthur CHARPENTIER - Rappels de probabilites statistiques
Comparaison de moyennes de deux echantillons
Considerons un test d'egalite de moyenne sur deux echantillons.
On dispose de deux echantillons, fx1; ; xng et fy1; ; ymg. On souhaite tester
8
:
H0 : X = Y
H0 : X6=Y
On rajoute une hypothese, X N(X; 2X
) et Y N(Y ; 2Y
), i.e.
X N
X;
2X
n
et Y N
Y ;
2Y
m
34

68. Arthur CHARPENTIER - Rappels de probabilites statistiques
Comparaison de moyennes de deux echantillons
−1 0 1 2 0.0 0.5 1.0 1.5 2.0
l ll l l l l l l ll l l l l
35

69. Arthur CHARPENTIER - Rappels de probabilites statistiques
Comparaison de moyennes de deux echantillons
Par independance entre X et Y , notons que = X Y suit une loi normale,
E() = X Y et V ar() =
2X
n
+
2Y
m
Donc sous H0, X Y = 0 et donc
D N
0;
2X
n
+
2Y
m
;
i.e. =
X Y r
2X
n
+
2Y
m
N(0; 1):
36

70. Arthur CHARPENTIER - Rappels de probabilites statistiques
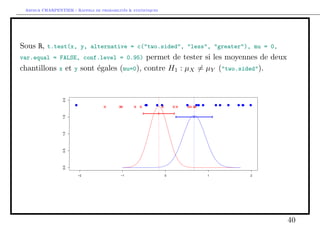
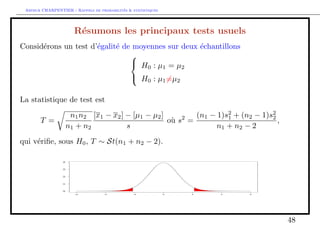
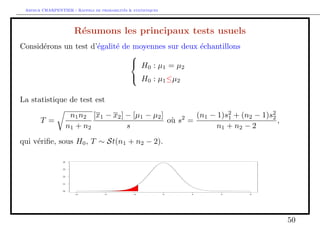
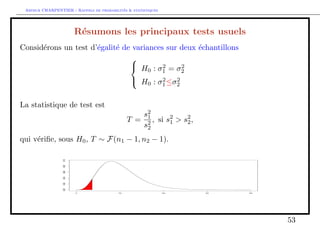
Comparaison de moyennes de deux echantillons
Probleme X et Y sont inconnus : on les remplace par des estimateurs bX et
bY ,
i.e. =
X Y r
b2X
n
+
b2Y
m
St();
ou est une fonction (compliquee) de n1 et n2.
On se donne un seuil d'acceptation 2 [0; 1] (e.g. 10%),
8
:
on accepte H0 si t=2 t1=2
on accepte H0 si t=2 ou t1=2
37

71. Arthur CHARPENTIER - Rappels de probabilites statistiques
REJET REJET
−2 −1 0 1 2
0.0 0.1 0.2 0.3 0.4 0.5
l ll l ll l l l ll ll l l
ACCEPTATION
38

72. Arthur CHARPENTIER - Rappels de probabilites statistiques
On peut se demander la probabilite p d'obtenir une valueur au moins aussi
grande que si H0 est vraie,
p = P(jZj jjjH0 vraie) = P(jZj jjjZ St()):
−2 −1 0 1 2
0.0 0.1 0.2 0.3 0.4 0.5
l ll l ll l l l ll ll l l
34.252 %
39

73. Arthur CHARPENTIER - Rappels de probabilites statistiques
Sous R, t.test(x, y, alternative = c(two.sided, less, greater), mu = 0,
var.equal = FALSE, conf.level = 0.95) permet de tester si les moyennes de deux
chantillons x et y sont egales (mu=0), contre H1 : X6= Y (two.sided).
−2 −1 0 1 2
0.0 0.5 1.0 1.5 2.0
l ll l l l ll l l l l l ll l
40

74. Arthur CHARPENTIER - Rappels de probabilites statistiques
REJET REJET
−2 −1 0 1 2
0.0 0.1 0.2 0.3 0.4 0.5
l ll l l l ll l l l l l ll l
ACCEPTATION
41

75. Arthur CHARPENTIER - Rappels de probabilites statistiques
−2 −1 0 1 2
0.0 0.1 0.2 0.3 0.4 0.5
l ll l l l ll l l l l l ll l
2.19 %
42

76. Arthur CHARPENTIER - Rappels de probabilites statistiques
Resumons les principaux tests usuels
Considerons un test d'egalite de moyenne sur un echantillon
8
:
H0 : = 0
H0 : 0
La statistique de test est
T =
p
n
x 0
s
ou s2 =
1
n 1
Xn
i=1
(xi x)2;
qui veri

77. e, sous H0, T St(n 1).
−6 −4 −2 0 2 4 6
0.0 0.1 0.2 0.3 0.4
43

78. Arthur CHARPENTIER - Rappels de probabilites statistiques
Resumons les principaux tests usuels
Considerons un test d'egalite de moyenne sur un echantillon
8
:
H0 : = 0
H0 : 0
La statistique de test est
T =
p
n
x 0
s
ou s2 =
1
n 1
Xn
i=1
(xi x)2;
qui veri

79. e, sous H0, T St(n 1).
−6 −4 −2 0 2 4 6
0.0 0.1 0.2 0.3 0.4
44

80. Arthur CHARPENTIER - Rappels de probabilites statistiques
Resumons les principaux tests usuels
Considerons un test d'egalite de variance sur un echantillon
8
:
H0 : 2 = 2
0
H0 : 26=2
0
La statistique de test est
T =
(n 1)s2
2
0
ou s2 =
1
n 1
Xn
i=1
(xi x)2;
qui veri