cours sur les variables aléatoires. l'objectif de ce cours est de faire découvrir aux étudiants en gestion les variables aléatoires dans le cadre de leurs cours de Probabilité
2. 2
Plan
• Variables aléatoires continues (v.a.c)
– Fonctions de densité et de répartition
– Distribution
– Théorème central limite
Lecture
• Chapitre 5
Exercices
• Exercices d’application
À faire: #5.1 à 5.3, 5.5 à 5.19, 5.22 à 5.25, 5.27 à 5.31, 5.34 à 5.44
• Vrai ou faux
– À faire: #1 à 19
• Choix multiples et autres
– À faire: #20 à 31
3. 3
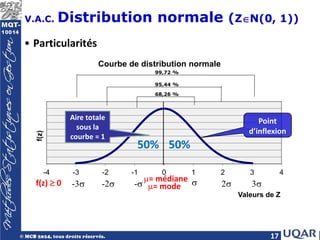
V.A.C. Fonction de densité de
probabilité
• Une variable aléatoire est continue (v.a.c.) si elle peut
prendre toutes les valeurs d’un intervalle de nombres réels.
• Exemples: Niveau de service atteint pendant une journée,
nombre moyen de clients en attente au dépanneur, rendement
d’une ligne de production d’une usine, etc.
• Fonction de densité
– Équivalent de la fonction de probabilité du v.a.d.:
– MAIS la probabilité que X prenne une valeur en particulier est nulle.
– On s’intéresse plutôt à déterminer la probabilité que la v.a. X
prenne n’importe quelle valeur dans un intervalle [a, b]
plutôt qu’une valeur particulière x.
( ) ( )
f x P X x
= =
( ) ( ) 0
f x P X x
= = =
( ) ( )
b
a
f x dx P a X b
= ≤ ≤
∫
4. 4
V.A.C. Fonction de densité de
probabilité: Exemple #1
• Soit X la v.a.c. représentant le temps total (temps d’attente
et de service), en heures, à la
banque. La fonction de densité
de X se présente comme suit:
• Fonction de densité de probabilité f(x)
– 2 formes: • Analytique
• Graphique
• Propriétés
o
o Aire sous la courbe = 1:
0 si 0
si 0 1
( )
2 si 1 2
0 si 2
x
x x
f x
x x
x
≤
≤ ≤
=
− ≤ ≤
≥
0
0,2
0,4
0,6
0,8
1
0 0,5 1 1,5 2
Densité
f(x)
Temps d'attente (en heures)
( )
f x x
= ( ) 2
f x x
= −
Aire sous la
courbe = 1
( ) 0 pour tout
f x x
≥ ∈
( ) 1
f x dx
∞
−∞
=
∫
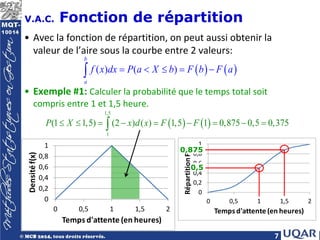
5. 5
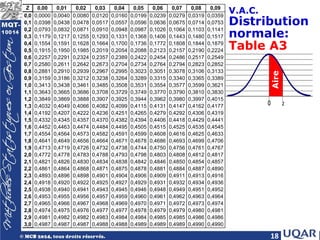
V.A.C. Calcul des probabilités
• Aire sous la courbe f entre 2 valeurs a et b
= probabilité que la v.a.c. X prenne une valeur dans l’intervalle [a, b]
• Exemple #1: Calculer la probabilité que le temps total soit compris
entre 1 et 1,5 heure.
• Comment fait-on
ce calcul si on ne
sait pas faire des
intégrales?
( ) ( ) ( )
b
a
P a X b f x d x
≤ ≤ =
∫
0
0,2
0,4
0,6
0,8
1
0 0,5 1 1,5 2
Densité
f(x)
Temps d'attente (en heures)
( )
1,5
1
(1 1,5) 2 ( )
P X x d x
≤ ≤ = −
∫
6. 6
V.A.C. Fonction de répartition
• La définition de la fonction de répartition est la même que
pour une v.a.d.: F(xi) = P(X ≤ xi)
• MAIS puisque les valeurs sont continues et non discrètes, on
va apporter une précision:
• Exemple #1: Calculer la probabilité que le temps total soit de 30
minutes.
( ) ( ) ( )
b
F X b P X b f x dx
−∞
= = ≤ = ∫
0
0,2
0,4
0,6
0,8
1
0 0,5 1 1,5 2
Densité
f(x)
Temps d'attente (en heures)
0,5
( 0,5) ( )
P X xd x
−∞
≤ =
∫
0
0,2
0,4
0,6
0,8
1
0 0,5 1 1,5 2
Répartition
F(x)
Temps d'attente (en heures)
0,125
7. 7
V.A.C. Fonction de répartition
• Avec la fonction de répartition, on peut aussi obtenir la
valeur de l’aire sous la courbe entre 2 valeurs:
• Exemple #1: Calculer la probabilité que le temps total soit
compris entre 1 et 1,5 heure.
( ) ( )
( ) ( )
b
a
f x dx P a X b F b F a
= < ≤ = −
∫
0
0,2
0,4
0,6
0,8
1
0 0,5 1 1,5 2
Densité
f(x)
Temps d'attente (en heures)
0
0,2
0,4
0,6
0,8
1
0 0,5 1 1,5 2
Répartition
F(x)
Temps d'attente (en heures)
0,5
0,875
( ) ( )
1,5
1
(1 1,5) (2 ) ( ) 1,5 1 0,875 0,5 0,375
P X x d x F F
≤ ≤ = − = − = − =
∫
8. 8
V.A.C. Fonction de répartition:
Exemple #2
• Soit X la v.a.c. représentant le temps
total (temps d’attente et de service),
en heures, à la banque. La fonction de
répartition ci-contre.
• Calculer
a) P(X ≤ 0,25)
b) P(X > 1,5)
c) P(0,25 ≤ X ≤ 1,5)
2
2
0 si 0
si 0 1
2
( )
2 1 si 1 2
2
1 si 2
x
x
x
F x
x
x x
x
≤
≤ ≤
=
− − ≤ ≤
≥
9. 9
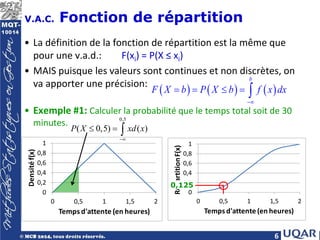
V.A.C. Propriétés d’une fonction de
répartition
• F(x) est définie,
• 0 ≤ F(x) ≤ 1
• Limites: F(-∞)=0 et F(∞+)=1
• F(x) est non-décroissante: si x ≤ y, alors F(x) ≤ F(y)
• dF(x) = f(x) ∀x où f(x) est continue
dx
• Remarque
– Lorsque X est une v.a.c., alors on a
Lorsqu’on dispose de la forme analytique de F (la fonction de
répartition), cette formule peut aussi être utilisée pour déterminer
la probabilité que X appartienne à un intervalle [a, b].
( )
( ) ( )
( ) ( )
( ) – ( )
b
a
P a X b P a X b P a X b
P a X b F b F a f x dx
< < = ≤ < = < ≤
= ≤ ≤ = = ∫
x
∀ ∈
10. 10
V.A.C. Mesures caractéristiques
d’une variable aléatoire
• Espérance mathématique
• Variance
• Écart type
[ ] ( )
E X xf x dx
∞
−∞
= ∫
[ ]
( ) ( ) ( )
2 2
2
2
2
( ) ( )
( ) ( )
Var X x E x f x dx E X E X
x f x dx xf x dx
∞
−∞
∞ ∞
−∞ −∞
=
− =
−
= −
∫
∫ ∫
( )
Var X
σ =
11. 11
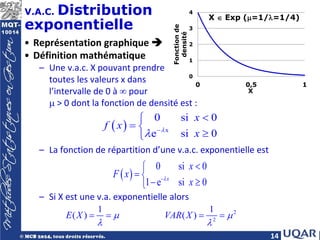
V.A.C. Distribution uniforme
• Notation: a et b = nombres réels où a < b
• Principe
X ∈ U(a, b)
– Une v.a.c. X obéit à une distribution uniforme sur un intervalle
[a, b] si sa densité de probabilité est donnée par:
(X suit une loi uniforme de paramètres a, b)
• Représentation
graphique
1
si
( )
0 ailleurs
a x b
f x b a
≤ ≤
= −
12. 12
V.A.C. Distribution uniforme
• Définition mathématique
– La fonction de répartition d’une
v.a.c. X qui obéit à une distribution
uniforme sur un intervalle [a, b]
est donnée par:
– Si X est une v.a. uniforme alors
• Exemple #3: Une machine à café prend 3 minutes faire un café
latté (180 sec.). Le temps X, exprimé en secondes, est uniforme et
indiqué sur le compteur de la machine (en commençant à 0). Vous
partez chercher du sucre.
a) Quelle est la probabilité que le temps indiqué à votre retour soit de
150 secondes ou plus?
b) Quelle est la moyenne de X?
0
si
-
( ) si
-
si
1
x a
x a
F x a x b
b a
x b
<
= ≤ ≤
≥
( )
2
2
( ) ( )
2 12
b a
a b
E X VAR X
µ σ
−
+
= = = =
13. 13
V.A.C. Distribution exponentielle
• Relation entre la loi de Poisson et la loi exponentielle
– Loi de Poisson: nombre d’occurrences (succès) dans un
intervalle de temps considéré (v.a.d.)
– Loi exponentielle: longueur de l’intervalle entre deux succès
consécutifs ou pour la réalisation d’un 1er succès (v.a.c.)
• Notation
– µ : temps moyen entre deux succès ou encore le temps
moyen pour obtenir un 1er succès (loi exponentielle)
– λ : nombre moyen de succès dans un intervalle de temps
considéré (loi de Poisson)
– Donc, µ (loi exponentielle) est l’inverse de λ (loi de Poisson)
• Principe
– Si une v.a.c. X représente le temps requis pour obtenir un 1re
succès ou le temps entre 2 succès consécutifs, alors X obéit à
une distribution exponentielle: X ∈ Exp (µ=1/λ)
(X suit une loi exponentielle de paramètre µ = 1/λ)
14. 14
V.A.C. Distribution
exponentielle
• Représentation graphique
• Définition mathématique
– Une v.a.c. X pouvant prendre
toutes les valeurs x dans
l’intervalle de 0 à ∞ pour
µ > 0 dont la fonction de densité est :
– La fonction de répartition d’une v.a.c. exponentielle est
– Si X est une v.a. exponentielle alors
( ) x
0 si 0
e si 0
x
f x
x
λ
λ −
<
=
≥
( ) -
0 si 0
1 e si 0
x
x
F x
x
λ
<
=
− ≥
2
2
1 1
( ) ( )
E X VAR X
µ µ
λ λ
= = = =
0
1
2
3
4
0 0,5 1
Fonction
de
densité
X
X ∈ Exp (µ=1/λ=1/4)
15. 15
V.A.C. Distribution exponentielle:
Exemple #4
• Un seul guichet est ouvert à la Banque Soldi. Les clients
arrivent à un taux moyen de 6 clients à l’heure.
a) Un client vient d’arriver. Quelle est la probabilité que le
prochain client entre dans 15 prochaines minutes?
b) Un client vient d’arriver. Quelle est la probabilité que
l’intervalle de temps entre l’arrivée de ce client et le prochain
soit compris entre 15 et 45 minutes?
c) Quelle est la probabilité qu’il y ait 10 clients ou plus dans la
prochaine heure?
d) Quel est le temps moyen d’arrivée entre 2 clients?
16. 16
V.A.C. Distribution normale (loi de
Gauss ou loi Gaussienne)
• Principe: Une v.a.c. X pouvant prendre toutes les valeurs réelles x
dans l’intervalle de -∞ à ∞+, pour , pour dont la
fonction de densité est
(X suit une loi normale de paramètres µ, σ2)
– Si X est une v.a. normale alors
• Standardisation (permet d’utiliser la table de loi N(0,1)):
– Transformer
où Z est une normale centrée réduite à l’aide de l’égalité:
– Permet l’utilisation de la table de la loi N(0,1).
2
1
2
1
( ) e
2
x
f x
µ
σ
σ π
−
−
=
2
( ) ( )
E X VAR X
µ σ
= =
µ ∈ 2
σ +
∈
2
( , ) (0,1)
X N Z N
µ σ
∈ ⇒ ∈
X
Z
µ
σ
−
=
x1 x2
µ
P(x1 ≤ X ≤ x2)
z1 z2
0
P(z1 ≤ Z ≤ z2)
17. 17
V.A.C. Distribution normale (Z∈N(0, 1))
• Particularités
-4 -3 -2 -1 0 1 2 3 4
f(z)
Valeurs de Z
Courbe de distribution normale
68,26 %
95,44 %
99,72 %
-2σ -σ 2σ
-3σ 3σ
σ
Point
d’inflexion
50% 50%
µ= mode
µ= médiane
f(z) ≥ 0
Aire totale
sous la
courbe = 1
19. 19
V.A.C. Distribution normale:
Exemple #5
• Une vérification nécessite en moyenne 2,4 minutes et un écart
type de 0,05 minute.
1. Des vérifications sont faites, trouvez la proportion de celles
dont le temps:
a) excède 2,5 minutes.
b) n’excède pas 2,32 minutes.
c) est compris entre 2,35 minutes et 2,46 minutes.
2. Trouvez la valeur de x telle que 5 % des vérifications prennent
un temps qui lui est supérieur.
20. 20
V.A.C. Théorème central
limite (TLC)
• Exemple d’explication (Exemple #6)
Soit l’expérience aléatoire consistant à choisir 6
personnes dans le département des ressources
humaines et à observer la suite de bilingues (B)
ou d’unilingues français (F) obtenus.
– Soit la v.a. X1 donnant
la probabilité que
chacune des personnes
choisies soit bilingue.
– Soit la v.a. X2 donnant
le nombre de personnes
bilingues obtenues dans
une équipe de 6.
http://www-groups.dcs.st-
and.ac.uk/~history/Biographies/Polya.html
George Pólya
(1887-1985)
0
0,25
0,5
0,75
1 2 3 4 5 6
P(X1 = x)
0 1 2 3 4 5 6
P(Y=y)
21. 21
V.A.C. Théorème central limite
• Principe: Soit X1, X2, X3,…, Xn des v. a. indépendantes de même
distribution de probabilité, d’espérances µi et de variances σi
2, i =
1, 2, … n, alors, lorsque n → ∞, la distribution de probabilité de la
v.a. Y est et converge toujours vers la loi normale.
• Convergence de la binomiale vers la normale
– Si X ∈ Bi (n, p) → N (np, npq)
– Conditions: Si p ≤ 0,5, np > 5 et si p > 0,5, nq ≥ 5
• Exemple #7: À la fin de sa formation en service à la clientèle, une
personne doit passer un examen objectif comportant 25 questions. Pour
chacune des questions une seule réponse est bonne parmi les 4 réponses
suggérées. Si cette personne répond aléatoirement aux questions, quelle
est la probabilité qu’elle ait exactement 1 bonne réponse?
1
n
i
i
Y X
=
= ∑
22. 22
Références
• Baillargeon G. (2020) Méthodes statistiques en gestion,
Éditions SMG.
• Bouchard J. (2011) Notes de cours MQT-1102, Université
Laval.
