Le chapitre traite des variables aléatoires discrètes, définies comme des fonctions associant des résultats d'épreuves aléatoires à des nombres réels. Il explique comment définir la loi de probabilité d'une variable aléatoire discrète et présente la fonction de répartition, qui indique la probabilité cumulée. Enfin, il aborde des propriétés telles que l'espérance mathématique, qui est la moyenne pondérée des valeurs possibles, et comment elle est affectée par des changements d'origine ou d'échelle.

1. Chapitre 6 :
Variable aléatoire à une dimension
Part I
Variable aléatoire discrète
1 Définition
Une variable aléatoire X est une fonction définie sur l’univers Ω et à valeurs dans R, qui à chaque résultat possible
(éventualité) e d’une épreuve aléatoire, associe un nombre réel X (e) = x
X : Ω → R
e 7→ X (e) = x
Une variable aléatoire est toujours notée par une majuscule : X, Y, . . .
Les valeurs que peut prendre une variable aléatoire sont représentées par une minuscule : x, y, ...
Une variable aléatoire est dite discrète si l’ensemble des valeurs prises par X est un ensemble fini X (Ω) =
{x1, x2, . . . , xk} ou un ensemble infini dénombrable X (Ω) = {x1, x2, . . . , xk, . . .}
X (Ω) est appelé domaine ou support de X, c’est l’ensemble des valeurs possibles de X
Exemples :
1) On tire une carte d’un jeu de 32 cartes (Ω = {as, roi, dame, valet, 10, 9, 8, 7}). Soit X la variable aléatoire
qui associe à la carte tirée une valeur numérique suivant la règle du jeu de belote (l’atout n’est pas pris en compte)
: 11 pour un as, 4 pour un roi, 3 pour une dame, 2 pour un valet et 0 pour les cartes qui portent les numéros 7,8
et 9.
Ω
X
( )X Ω
:
:
As Roi Dame Valet 10 9 8 7
11 4 3 2 10 0 jx
ie
On obtient X (Ω) = {0, 2, 3, 4, 10, 11} , qui est un ensemble fini, donc X est une variable aléatoire discrète.
2) Soit l’expérience qui consiste à jeter 2 fois une pièce de monnaie et soit X la variable aléatoire définie par le
nombre de Piles obtenues.
Ω = {(P, F) , (P, P) , (F, P) , (F, F)}
Ω
X
( )X Ω
:
:
(P,P) (P,F) (F,P) (F,F)
2 1 1 0 jx
ie
L’ensemble des valeurs possibles de la variable aléatoire X est donc : X (Ω) = {0, 1, 2}
X est une variable aléatoire discrète qui peut prendre les valeurs 0, 1 et 2.
1

2. 2 Loi de probabilité d’une variable aléatoire discrète
Soit X une variable aléatoire discrète dont l’ensemble des valeurs possibles est donné par X (Ω) = {x1, x2, . . . xi, . . . , xk} .
Associer à chacune des valeurs possibles de X la probabilité qui lui correspond, c’est définir la loi de probabilité
(ou distribution de probabilité) de la variable aléatoire X.
A toute valeur possible xi de la variable aléatoire X, on fait correspondre un nombre Pi, compris entre 0 et 1,
défini par :
Pi = P(X = xi), i : 1 . . . k
avec Pi ≥ 0 et
kP
i=1
Pi = 1
2.1 Définition
La loi de probabilité d’une variable aléatoire discrète est définie par l’ensemble des couples (xi, Pi) :
X : x1 x2 . . . xi . . . xk
Pi = P(X = xi) : P1 P2 . . . Pi . . . Pk
Parfois cette liste de valeurs caractérisant un tableau de distribution d’une variable aléatoire peut être résumée
par une formule mathématique. Si c’est le cas, la loi de probabilité sera définie par une fonction :
f : X (Ω) −→ [0, 1]
x 7−→ f (x) = P(X = x)
Suite de l’exemple 2 :
Reprenons l’exemple qui consiste à jeter 2 fois une pièce de monnaie. La variable aléatoire X est définie par "le
nombre de piles obtenus". X peut prendre les valeurs 0,1 et 2 (X (Ω) = {0, 1, 2})
Pour déterminer la loi de probabilité de la variable aléatoire X, il suffit d’associer, à chacune des valeurs possibles
de X, la probabilité correspondante :
P1 = P(X = 0) = P ({(F, F)}) =
1
4
P2 = P(X = 1) = P ({(P, F) , (F, P)}) =
1
2
P3 = P(X = 2) = P ({(P, P)}) =
1
4
La loi de probabilité de X est donnée par
X : 0 1 2
Pi = P(X = xi) :
1
4
1
2
1
4
avec
P
x∈X(Ω)
P(X = x) = 1
2.2 Représentation graphique de la distribution d’une variable aléatoire discrète
La représentation graphique de la loi de probabilité dans le cas discret se fait à l’aide d’un diagramme en bâtons
3 Fonction de répartition
3.1 Définition
Soit X une variable aléatoire discrète, la fonction de répartition, notée F, de la v.a X est une fonction positive non
décroissante, définie par :
F : R −→ [0, 1]
x 7−→ F (x) = P (X < x) =
P
xi<x
P (X = xi)
F (x) = P (X < x) : indique la probabilité que la v.a X prenne une valeur strictement inférieure à x.
2

3. 3.2 Formulation de la Fonction de répartition
D’une manière générale, soit X une variable aléatoire discrète définie par sa loi de probabilité :
X : x1 x2 . . . xi . . . xk
Pi = P(X = xi) : P1 P2 . . . Pi . . . Pk
, avec
kP
i=1
P (X = xi) = 1
La formulation de la fonction de répartition de X est donnée par :
F (x) = P (X < x) =
⎧
⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨
⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩
0 si x ≤ x1
P1 si x1 < x ≤ x2
P1 + P2 si x2 < x ≤ x3
...
...
...
P1 + P2 + · · · + Pi−1 si xi−1 < x ≤ xi
...
...
...
P1 + P2 + · · · + Pk−1 si xk−1 < x ≤ xk
...
...
...
kP
i=1
Pi = 1 si x > xk
3.3 Représentation graphique de la fonction de répartition
La représentation graphique de la fonction de répartition d’une v.a discrète est une courbe en escalier
1x
( )F x
1
P
X
1
2x 3x ix 1ix + kx
1 2
P P+
)
)
)
)
)
1
1
i
jj
P
−
=∑
1
i
jj
P=∑
Application à l’exemple 2 :
F (x) = P (X < x) =
⎧
⎪⎪⎪⎪⎨
⎪⎪⎪⎪⎩
0 si x ≤ 0
1
4
si 0 < x ≤ 1
3
4
si 1 < x ≤ 2
1 si 2 < x ≤ 3
0
( )F x
X
1
1 2
3
4
)
)
)
1
4
- Calculer F (1, 5)?
3

4. F (1, 5) = P (X < 1, 5) = P (X ≤ 1) = P (X < 2) = P (X = 0) + P (X = 1) =
1
4
+
1
2
=
3
4
- Déterminer la probabilité que la variable aléatoire X prenne une valeur strictement supérieure à 0, 5 et
inférieure ou égale à 1, 2?
P (0, 5 < X ≤ 1, 2) = P (X ≤ 1, 2) − P (X ≤ 0, 5) = P (X < 2) − P (X < 1) = F (2) − F (1) =
1
2
, ou encore
P (0, 5 < X ≤ 1, 2) = P (X = 1) =
1
2
3.4 Propriétés de la fonction de répartition
1. ∀x ∈ R, 0 ≤ F (x) ≤ 1
2. La fonction de répartition représente des probabilités cumulées croissantes. Partant de la définition de la
fonction de répartition, on peut définir les probabilités cumulées décroissantes :
G (x) = P (X ≥ x) =
P
xi≥x
P (X = xi) = 1 −
P
xi<x
P (X = xi)
= 1 − P (X < x) = 1 − F (x)
3. La fonction de répartition est une fonction non décroissante (c.-à-d. croissante au sens large) :
Soit x et x0
deux réels tels que x > x0
alors F (x) ≥ F (x0
)
( )F x
X
1
1x
3( )F x )
)
2x 3x
2( )F x
'x
)
x x
4. ∀xi ∈ X (Ω) , F est continue à gauche de xi
Ã
lim
x→x−
i
F (x) = F (xi)
!
mais pas à droite
Ã
lim
x→x+
i
F (x) = F (xi+1)
!
5. La connaissance de la fonction de répartition nous permet de déterminer la loi de probabilité d’une variable
aléatoire discrète :
On a F (xi) = P (X < xi) =
i−1P
j=1
P (X = xj) = P (X = x1) + P (X = x2) + · · · + P (X = xi−1)
= P1 + P2 + · · · + Pi−1 =
i−1P
j=1
Pj
De même F (xi+1) = P (X < xi+1) =
iP
j=1
Pj
⇒ F (xi+1) − F (xi) =
iP
j=1
Pj −
i−1P
j=1
Pj = Pi = P (X = xi)
Exemple 3 :
Soit X une variable aléatoire de fonction de répartition :
4

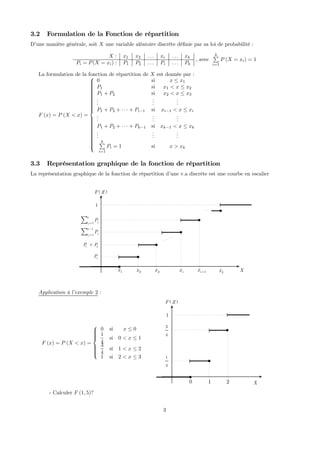
5. F (x) =
⎧
⎪⎪⎪⎪⎪⎪⎪⎪⎨
⎪⎪⎪⎪⎪⎪⎪⎪⎩
0 si x ≤ 1
1
4
si 1 < x ≤ 2
1
3
si 2 < x ≤ 3
2
3
si 3 < x ≤ 4
1 si x > 4
- Déterminer la loi de probabilité de X?
Il faut tout d’abord remarquer que la variable aléatoire en question est une variable aléatoire discrète puisque
sa fonction de répartition est discontinue et constante par intervalle.
F (x) prend la valeur 0, ∀x ≤ x1 = 1, en particulier F (x1) = 0.
Pour x ∈ ]x1 = 1, x2 = 2], on a F (x) =
1
4
, en particulier F (x2) =
1
4
.
Pour x ∈ ]x2 = 2, x3 = 3], on a F (x) =
1
3
, en particulier F (x3) =
1
3
.
Pour x ∈ ]x3 = 3, x4 = 4], on a F (x) =
2
3
, en particulier F (x4) =
2
3
.
∀x ≥ x4, F (x) prend la valeur 1.
Ainsi, la variable aléatoire X peut prendre les valeurs x1 = 1, x2 = 2, x3 = 3 et x4 = 4 (X (Ω) = {1, 2, 3, 4}).
F (x2) − F (x1) = P (X = x1) = P1 =
1
4
; F (x3) − F (x2) = P (X = x2) = P2 =
1
12
F (x4) − F (x3) = P (X = x3) = P3 =
1
3
; et puisque
4P
i=1
Pi = 1, alors P4 = 1 −
µ
1
4
+
1
12
+
1
3
¶
=
1
3
La loi de probabilité de X est donc
X : 1 2 3 4
Pi :
1
4
1
12
1
3
1
3
4 Les paramètres descriptifs d’une variable aléatoire discrète
4.1 Espérance mathématique
L’espérance mathématique d’une v.a discrète est égale à la somme des valeurs possibles xi pondérées par leurs
probabilités Pi
E (X) =
kX
i=1
xiP (X = xi)
Si la variable n’est pas finie (c.-à-d. X (Ω) est un ensemble infini dénombrable), alors l’espérance mathématique
est donnée par :
E (X) =
∞X
i=1
xiP (X = xi)
Dans ce cas, E (X) n’existe que si la série
∞P
i=1
xiP (X = xi) est convergente (chapitre I -Math I)
N.B : Pour le reste du cours, on utilisera la notation suivante :E (X) =
P
x∈X(Ω)
xP (X = x)
4.1.1 Propriétés de l’espérance mathématique
a/ l’espérance mathématique d’une constante est égale à la constante elle même.
E (a) = a
b/ changement d’origine :
E (X + b) =
P
x∈X(Ω)
(x + b) P (X = x) =
P
x∈X(Ω)
xP (X = x) + b
P
x∈X(Ω)
P (X = x) = E (X) + b
E (X + b) = E (X) + b
5

6. c/ changement d’échelle :
E (aX) =
P
x∈X(Ω)
axP (X = x) = a
P
x∈X(Ω)
xP (X = x) = aE (X)
E (aX) = aE (X)
b/ et c/ =⇒ E (aX + b) = aE (X) + b
d/ La somme des écarts, pondérées par les probabilités, entre les valeurs xi et l’espérance mathématique E (X)
est nulle :
E (X − E (X)) =
P
x∈X(Ω)
(x − E (X)) P (X = x) =
P
x∈X(Ω)
xP (X = x) − E (X)
P
x∈X(Ω)
P (X = x)
= E (X) − E (X) = 0
E (X − E (X)) = 0
4.1.2 Espérance mathématique d’une fonction de X
Soit X une variable aléatoire discrète sur laquelle on applique une fonction numérique quelconque ψ.
X
Ω ( )X IRΩ ⊂
ψ
IR
Xψ
ψ (X) est aussi une variable aléatoire discrète.
Si elle existe, l’espérance mathématique de ψ (X) est :
E (ψ (X)) =
X
x∈X(Ω)
ψ (x) P (X = x) =
X
i
ψ (xi) P (X = xi)
Les moments non centrés : ψ (X) = Xk
Le moment non centré d’ordre k de X, noté mk est défini par :
mk = E
¡
Xk
¢
=
X
x∈X(Ω)
xk
P (X = x)
pour k = 0 m0 = E (1) = 1
pour k = 1 m1 = E (X) ⇒ l’espérance est le moment non centré d’ordre 1
pour k = 2 m2 = E
¡
X2
¢
=
P
x∈X(Ω)
x2
P (X = x)
Les moments centrés : ψ (X) = [X − E (X)]k
Le moment centré d’ordre k de X, noté µk est défini par :
µk = E [X − E (X)]
k
=
X
x∈X(Ω)
(x − E (X))
k
P (X = x)
pour k = 0 µ0 = E (1) = 1
pour k = 1 µ1 = E (X − E (X)) = 0
pour k = 2 µ2 = E (X − E (X))2
= E
³
X2
− 2XE (X) + E (X)2
´
= E
¡
X2
¢
− 2 [E (X)]2
+ [E (X)]2
= E
¡
X2
¢
− [E (X)]2
= m2 − [m1]2
6

7. 4.2 Variance d’une variable aléatoire discrète
On appelle variance de X et on note, V (X) ou σ2
X, le nombre réel positif, s’il existe défini par :
V (X) = σ2
X = E (X − E (X))2
=
P
x∈X(Ω)
(x − E (X))2
P (X = x)
=
P
x∈X(Ω)
x2
P (X = x) − 2E (X)
P
x∈X(Ω)
xP (X = x) + E (X)
2 P
x∈X(Ω)
P (X = x)
= E
¡
X2
¢
− [E (X)]2
4.2.1 Propriétés de la variance
a/ La variance d’une constante est nulle :
V (a) = E (a − E (a))2
= E (a − a)2
= 0
b/ changement d’origine
contrairement à l’espérance, la variance ne change pas avec un changement d’origine.
V (X + b) = E ((X + b) − E (X + b))2
= E (X + b − E (X) − b)2
= E (X − E (X))2
= V (X)
c/ changement d’échelle
V (aX) = E ((aX) − E (aX))
2
= E ((aX) − aE (X))
2
= E [a (X − E (X))]
2
= a2
E (X − E (X))
2
= a2
V (X)
b/ Théorème de Koenig
Ce théorème stipule que la variance est égale à la différence entre le moment non centré d’ordre 2 et le carré
du moment centré d’ordre 1 :
V (X) = E (X − E (X))2
= E
¡
X2
¢
− 2 [E (X)]2
+ [E (X)]2
= E
¡
X2
¢
− [E (X)]2
= m2 − [m1]2
Application à l’exemple 2 :
X : 0 1 2
Pi = P(X = xi) :
1
4
1
2
1
4
E (X) =
P
x∈X(Ω)
xP (X = x) = 0 ×
1
4
+ 1 ×
1
2
+ 2 ×
1
4
= 1
E
¡
X2
¢
=
P
x∈X(Ω)
x2
P (X = x) = 0 ×
1
4
+ 1 ×
1
2
+ 4 ×
1
4
=
3
2
V (X) = E
¡
X2
¢
− [E (X)]
2
=
3
2
− (1)
2
=
1
2
Si Y = 2X + 1, alors
E (Y ) = E (2X + 1) = 2E (X) + 1 = 3 et V (Y ) = V (2X + 1) = 4V (X) = 2
7

8. Deuxième partie
Variable aléatoire continue
1 Définition
Une variable aléatoire continue est une application X de Ω dans l’ensemble des réels R, telle que X (Ω) soit un
intervalle de R (c.-à-d. X (Ω) est un ensemble infini non dénombrable)
Par exemple, si X est telle que X (Ω) = [a, b] ⊂ R, ceci signifie que X prend toutes les valeurs réelles comprises
entre a et b. Dans ce cas, il n’est pas possible d’énumérer tous les éléments de X (Ω) et de calculer leur probabilité.
Pour une variable aléatoire continue, les éventualités sont si nombreuses qu’intuitivement, on est amené à attribuer
à chacune des valeurs une probabilité nulle. Cependant, on peut calculer la probabilité d’obtenir une valeur appar-
tenant à un intervalle donné [P (c ≤ X < d) = F (d)−F (c)] ou inférieure à une valeur donnée [P (X < x) = F (x)].
le fait de privilégier les événements décrits à l’aide d’intervalles, montre l’importance de la fonction de répartition
pour une variable aléatoire continue.
Exemple :
Soit l’expérience qui consiste à lancer des fléchettes vers une cible circulaire de rayon r et à s’intéresser aux points
de contact de la fléchette avec le plan de la cible. Dans ce cas, l’univers Ω est un ensemble infini non dénombrable :
Ω =
©
(x, y) /x2
+ y2
≤ r2
ª
, les couples (x, y) désignent les coordonnées des points de contacts.
Soit X la variable aléatoire définie par "la distance qui sépare le point de contact du centre de la cible".
L’ensemble des valeurs possibles de X est donc : X (Ω) = [0, r] .
X est une variable aléatoire continue puisqu’elle peut prendre n’importe quelle valeur à l’intérieure de l’intervalle
[0, r] .
{ }2 2 2
( , )/x y x ryΩ = + ≤
( ) [ ]0,X rΩ = ⊂ R
. r
d
x
y
point de contact, entre la fléchette et la cible, de coordonnées (x,y)
X
2 Fonction de répartition d’une variable aléatoire continue
2.1 Définition
Une variable aléatoire continue est caractérisée par sa fonction de répartition continue sur R, la définition de
cette dernière est identique à celle d’une variable discrète mais sa formulation mathématique change
F : R −→ [0, 1]
x 7−→ F (x) = P (X < x) =
R x
−∞
f(t)dt
où f(t) est appelée densité de probabilité de la variable aléatoire X
8

9. 2.2 Propriétés de la fonction de répartition
a/ ∀x ∈ R, 0 ≤ F (x) ≤ 1
b/ F est une fonction croissante et vérifie lim
x→−∞
F (x) = 0 et lim
x→+∞
F (x) = 1. [si X (Ω) = R, la courbe de F
admet comme asymptotes horizontales les droites (y = 0) et (y = 1) .
c/ F est une fonction continue et dérivable presque partout
d/ Probabilité attachée à un point
Soit x et x + ε (ε > 0) deux réels quelconques, on a
P (x ≤ X < x + ε) = F (x + ε) − F (x)
Si on fait tendre ε vers 0, l’intervalle [x, x + ε[ se réduit à la seule valeur {x} . Dans ces conditions :
P (X = x) = lim
ε→0
P (x ≤ X < x + ε) = lim
ε→0
F (x + ε) − F (x)
La continuité de F entraîne donc lim
ε→0
F (x + ε) = F (x)
D’où P (X = x) = F (x) − F (x) = 0.
Pour une variable aléatoire continue, la probabilité d’observer une valeur réelle x donnée est donc nulle
e/ Probabilité attachée à un intervalle
P (X ∈ [a, b]) = P (a ≤ X ≤ b) = P (a < X ≤ b) = P (a ≤ X < b) = P (a < X < b) = F (b) − F (a)
=
R b
−∞
f(t)dt −
R a
−∞
f(t)dt
=
R b
a
f(t)dt
2.3 Représentation graphique de la fonction de répartition d’une v.a.c
La courbe représentative de la fonction de répartition d’une V.A.C a l’allure suivante :
1y =
( )F x
xo
( )si X Ω = R
1y =
( )F x
xo
( ) [ ]si ,X a bΩ =
a b
3 Densité de probabilité
3.1 Définition
Soit X une variable aléatoire continue de fonction de répartition F (x) .
La connaissance de la fonction de répartition nous permet de calculer la probabilité de voir X prendre une valeur
à l’intérieure de n’importe quel intervalle de bornes x et x + ∆x (x ∈ X (Ω)). En effet :
P (x < X < x + ∆x) = F (x + ∆x) − F (x) .
La probabilité moyenne de l’intervalle par unité de longueur est donné par :
P (x < X < x + ∆x)
∆x
=
F (x + ∆x) − F (x)
∆x
(∆x étant la longueur de l’intervalle [x, x + ∆x] .
On appelle densité de probabilité f (.) au point x, la valeur limite de probabilité moyenne sur l’intervalle
[x, x + ∆x] lorsque la longueur ∆x de cet intervalle tend vers 0 :
f (x) = lim
∆x→0
F (x + ∆x) − F (x)
∆x
= F0
(x)
Conséquence :
9

10. La probabilité pour que la variable aléatoire X prenne une valeur x à l’intérieure d’un intervalle infinitésimal de
longueur dx est égale au produit f (x) dx, appelé probabilité élémentaire.
dx infinitésimal ⇒
F (x + dx) − F (x)
dx
= f (x) ⇒ F (x + dx) − F (x) = f (x) dx
⇒ P (x < X < x + dx) = f (x) dx
La probabilité attachée à un intervalle [a, b] apparaît donc comme la somme, prise entre a et b, des probabilités
élémentaires :
P (a < X < b) =
R b
a
f(x)dx = F (b) − F (a)
a bdx
f(x)
probabilité élémentaire : f(x)dx
3.2 Propriétés de la fonction densité
a/ ∀x ∈ R, f (x) ≥ 0.
F (x) étant une fonction croissante, sa dérivé F0
(x), c.-à-d. la fonction densité f(x), est donc positive ou nulle.
b/
R +∞
−∞
f(x)dx = P (X ∈ R) = P (Ω) = 1
ou encore
R +∞
−∞
f(x)dx = lim
b→+∞
R b
−∞
f(x)dx = lim
b→+∞
F (b) = 1
Remarque : les propriétés a/ et b/ seront utilisées pour montrer qu’une fonction f(x) est une densité de
probabilité.
d/ La densité de probabilité f (x) est une fonction continue sur R, sauf éventuellement en un nombre fini de
points
c/ Puisque lim
x→−∞
F (x) = 0 et lim
x→+∞
F (x) = 1, alors
µ
lim
x→±∞
F (x)
¶0
= 0
⇔ lim
x→±∞
F0
(x) = lim
x→±∞
f (x) = 0
d/ La courbe de la fonction densité f (x) prend, parmi beaucoup d’autres les allures suivantes :
f(x)
x
( )si X Ω = R
f(x)
( ) [ ]si ,X a bΩ =
a b
Exemple 1 :
Soit X une variable aléatoire continue ne prenant que des valeurs comprises entre 2 et 4, et dont la densité de
probabilité est égale à f (x) = 1 − kx.
Déterminer la constante k et en déduire la fonction de répartition ?
10

11. Solution :
Il faut que f (x) ≥ 0 et
R +∞
−∞
f(x)dx = 1
f (x) ≥ 0 ⇒ kx < 1 ⇒ k <
1
x
, or 2 ≤ x ≤ 4 ⇒
1
4
≤
1
x
≤
1
2
, donc k <
1
4
.
R +∞
−∞
f(x)dx = =
R 2
−∞
f(x)
|{z}
=0
dx +
R 4
2
f(x)
|{z}
=(1−kx)
dx +
R +∞
4
f(x)
|{z}
=0
dx
=
R 4
2
(1 − kx)dx =
∙
x −
1
2
kx2
¸4
2
= 2 − 6k
R +∞
−∞
f(x)dx = 1 ⇔ 2 − 6k = 1 donc k =
1
6
La densité de probabilité de X est donnée par : f (x) =
(
1 −
x
6
si x ∈ [2, 4]
0 sinon
On a par définition F : R −→ [0, 1]
x 7−→ F (x) = P (X < x) =
R x
−∞
f(t)dt
Pour x < 2 F (x) =
R x
−∞
f(t)dt = 0
Pour 2 ≤ x ≤ 4 F (x) =
R x
−∞
f(t)dt =
R 2
−∞
f(t)dt +
R x
2
f(t)dt =
R x
2
(1 −
t
6
)dt =
∙
t −
1
12
t2
¸x
2
= x −
x2
12
−
5
3
Pour x > 4 F (x) =
R x
−∞
f(t)dt =
R 2
−∞
f(t)dt +
R 4
2
f(t)dt +
R x
4
f(t)dt =
R 4
2
(1 −
t
6
)dt = 1
⇒ F (x) =
⎧
⎪⎨
⎪⎩
0 si x < 2
x −
x2
12
−
5
3
si 2 ≤ x ≤ 4
1 si x > 4
Exemple 2 :
Soit X une variable aléatoire continue de fonction de répartition :
F (x) =
½
1 − e−x
si x ≥ 0
0 sinon
Déterminer la densité de probabilité de X.
On sait que f (x) = F0
(x)
f (x) = (1 − e−x
)
0
= e−x
si x ≥ 0
f (x) = 0 sinon
4 Les paramètres descriptifs d’une distribution continue
4.1 Espérance mathématique
On appelle espérance mathématique de la V.A.C X, et on note E (X) , le nombre réel s’il existe défini par :
E (X) =
R +∞
−∞
xf(x)dx
L’existence de E (X) est liée à la convergence de l’intégrale.
4.1.1 Espérance mathématique d’une fonction de X
Soit X une variable aléatoire continue sur laquelle on applique une fonction numérique quelconque ψ.
Si la fonction ψ admet une espérance mathématique, alors :
E (ψ (X)) =
R +∞
−∞
ψ (x) f(x)dx
a/ Les moments non centrés : ψ (X) = Xk
Le moment non centré d’ordre k de X, noté mk est défini par :
mk = E
¡
Xk
¢
=
R +∞
−∞
xk
f(x)dx
pour k = 0 m0 = E (1) = 1
pour k = 1 m1 = E (X) ⇒ l’espérance est le moment non centré d’ordre 1
pour k = 2 m2 = E
¡
X2
¢
=
R +∞
−∞
x2
f(x)dx
11

12. b/ Les moments centrés : ψ (X) = [X − E (X)]
k
Le moment centré d’ordre k de X, noté µk est défini par :
µk (X) = E [X − E (X)]k
=
R +∞
−∞
(x − E (X))k
f(x)dx
pour k = 0 µ0 = E (1) = 1
pour k = 1 µ1 = E (X − E (X)) = 0
pour k = 2 µ2 = E (X − E (X))2
=
R +∞
−∞
³
x2
− 2xE (X) + E (X)2
´
f(x)dx
=
R +∞
−∞
x2
f(x)dx − 2E (X)
R +∞
−∞
f(x)dx + E (X)
2 R +∞
−∞
f(x)dx
= E
¡
X2
¢
− 2E (X)
2
+ E (X)
2
= E
¡
X2
¢
− [E (X)]2
= m2 − [m1]2
4.1.2 Propriétés de l’espérance mathématique
a/ l’espérance mathématique d’une constante est égale à la constante elle même.
E (a) =
R +∞
−∞
af(x)dx = a
Z +∞
−∞
f(x)dx
| {z }
1
= a
b/ changement d’origine :
E (X + b) =
R +∞
−∞
(x + b) f(x)dx =
R +∞
−∞
xf(x)dx + b
R +∞
−∞
f(x)dx = E (X) + b
E (X + b) = E (X) + b
c/ changement d’échelle :
E (aX) =
R +∞
−∞
axf(x)dx = a
R +∞
−∞
xf(x)dx = aE (X)
E (aX) = aE (X)
b/ et c/ =⇒ E (aX + b) = aE (X) + b
d/ La somme des écarts, pondérées par les probabilités élémentaires, entre les valeurs x et l’espérance mathéma-
tique E (X) est nulle :
E (X − E (X)) =
R +∞
−∞
(x − E (X)) f(x)dx =
R +∞
−∞
xf(x)dx − E (X)
R +∞
−∞
f(x)dx
= E (X) − E (X) = 0
E (X − E (X)) = 0
4.2 Variance d’une variable aléatoire continue
On appelle variance de X et on note, V (X) ou σ2
X, le nombre réel positif, s’il existe, défini par :
V (X) = σ2
X = E (X − E (X))2
=
R +∞
−∞
(x − E (X))
2
f(x)dx
= µ2 = E
¡
X2
¢
− [E (X)]2
= m2 − [m1]2
12

13. Troisième partie
La fonction génératrice des moments
1 Définition
Soit X une variable aléatoire. On appelle fonction génératrice des moments de la v.a. X, la fonction MX (t)
définie par :
MX (t) = E
¡
etX
¢
=
P
x∈X(Ω)
etx
P (X = x) si X est une v.a. discrète
=
R +∞
−∞
etx
f(x)dx si X est une v.a. continue
L’intérêt de la fonction génératrice des moments réside dans la possibilité de calculer rapidement les moments
non centrés d’ordre k.
1.1 Propriétés de la fonction génératrice des moments
a/ MX (t) > 0 et MX (0) = 1
∀X, etX
> 0 ⇒ MX (t) = E
¡
etX
¢
> 0
MX (0) = E
¡
e0
¢
= E (1) = 1
b/ Soit Y = aX + b
MY (t) = E
¡
etY
¢
= E
¡
et(aX+b)
¢
= E
¡
eatX
.etb
¢
= etb
E
¡
eatX
¢
= etb
.MX (at) .
c/ La dérivée première de MX (t) en t = 0 est égale à l’espérance mathématique de X
∂MX (t)
∂t
¯
¯
¯
¯
t=0
= E (X)
— Cas où X est une v.a. discrète :
∂MX (t)
∂t
=
∂
P
x∈X(Ω)
etx
P (X = x)
∂t
=
P
x∈X(Ω)
P (X = x)
∂etx
∂t
=
P
x∈X(Ω)
xetx
P (X = x)
⇒
∂MX (t)
∂t
¯
¯
¯
¯
t=0
=
P
x∈X(Ω)
xe0x
P (X = x) =
P
x∈X(Ω)
xP (X = x) = E (X)
— Cas où X est une v.a. continue
∂MX (t)
∂t
=
∂
R +∞
−∞
etx
f(x)dx
∂t
=
R +∞
−∞
f(x)dx
∂etx
∂t
=
R +∞
−∞
xetx
f(x)dx
⇒
∂MX (t)
∂t
¯
¯
¯
¯
t=0
=
R +∞
−∞
xf(x)dx = E (X)
Plus généralement, la dérivée d’ordre k de la fonction MX (t) , évaluée au point t = 0, est égale au moment
non centré d’ordre k :
∂k
MX (t)
∂tk
¯
¯
¯
¯
t=0
= E
¡
Xk
¢
= mk, k ∈ N
⇒ la variance de X est donc :
V (X) = E
¡
X2
¢
− [E (X)]
2
=
∂2
MX (t)
∂t2
¯
¯
¯
¯
t=0
−
∙
∂MX (t)
∂t
¯
¯
¯
¯
t=0
¸2
Exemple1 :
Soit X une variable aléatoire de loi de probabilité : P (X = x) =
1
(2)
x+1 x ∈ N
Calculer la fonction génératrice des moments. En déduire E (X) et V (X) .
Solution :
X est donc une variable aléatoire discrète.
⇒ MX (t) = E
¡
etX
¢
=
P
x∈X(Ω)
etx
P (X = x) =
+∞P
x=0
etx
µ
1
2
¶x+1
=
1
2
+∞P
x=0
µ
et
2
¶x
13

14. +∞P
x=0
µ
et
2
¶x
est une série géométrique qui ne converge que si
et
2
< 1
µ
et
2
> 0 ∀t
¶
En effet,
+∞P
x=0
µ
et
2
¶x
= lim
n→∞
nP
x=0
µ
et
2
¶x
= lim
n→∞
Ã
1 +
et
2
+
µ
et
2
¶2
+ · · · +
µ
et
2
¶n
!
= lim
n→∞
⎛
⎜
⎜
⎜
⎝
1 −
µ
et
2
¶n+1
1 −
et
2
⎞
⎟
⎟
⎟
⎠
=
1
1 −
et
2
si t < Log2
⇒ MX (t) =
1
2
1
1 −
et
2
= (2 − et
)
−1
si t < Log2
∂MX (t)
∂t
=
∂ (2 − et
)
−1
∂t
= et
(2 − et
)
−2
⇒ E (X) =
∂MX (t)
∂t
¯
¯
¯
¯
t=0
= 1
∂2
MX (t)
∂t2
= et
(2 − et
)
−2
+ et
h
−2 (−et
) (2 − et
)
−3
i
= et
(2 − et
)
−2
+ 2e2t
(2 − et
)
−3
= et
(2 − et
)
−2
h
1 + 2et
(2 − et
)
−1
i
⇒ E
¡
X2
¢
=
∂2
MX (t)
∂t2
¯
¯
¯
¯
t=0
= 3 ⇒ V (X) = E
¡
X2
¢
− [E (X)]
2
= 2
Exemple2 :
Soit θ une constante strictement positive et soit f(x) =
½
θe−θx
si x ≥ 0
0 sinon
1. Vérifier que f est bien une densité de probabilité.
2. Calculer la fonction génératrice des moments. En déduire E (X) et V (X) .
Solution :
1. On a f(x) ≥ 0 ∀x ∈ R
R +∞
−∞
f(x)dx =
R 0
−∞
f(x)dx +
R +∞
0
f(x)dx =
R +∞
0
θe−θx
dx = −
£
e−θx
¤+∞
0
= 1
f est bien la densité de probabilité d’une variable aléatoire X.
2. MX (t) =
R +∞
−∞
etx
f(x)dx =
R 0
−∞
etx
f(x)dx +
R +∞
0
etx
f(x)dx =
R +∞
0
etx
θe−θx
dx =
R +∞
0
θe(t−θ)x
dx
⇔ MX (t) = θ
R +∞
0
e(t−θ)x
dx = θ
∙
1
t − θ
e(t−θ)x
¸+∞
0
=
−θ
t − θ
=
θ
θ − t
si t < θ.
( il faut que t < θ ⇔ t − θ < 0 pour que lim
x→+∞
e(t−θ)x
= 0 sinon l’intégrale ne serait pas convergente)
∂MX (t)
∂t
=
θ
(θ − t)
2 ⇒ E (X) =
∂MX (t)
∂t
¯
¯
¯
¯
t=0
=
1
θ
et
∂2
MX (t)
∂t2
=
2θ
(θ − t)
3 ⇒ E
¡
X2
¢
=
∂2
MX (t)
∂t2
¯
¯
¯
¯
t=0
=
2
θ2
⇒ V (X) = E
¡
X2
¢
− [E (X)]
2
=
2
θ2 −
1
θ2 =
1
θ2 .
14

15. Quatrième partie
Transformation d’une variable aléatoire
1 Transformation d’une v.a. en une variable centrée réduite
Une variable aléatoire est dite “centrée” si son espérance est égale à 0. Si en plus, sa variance est égale à 1, alors
elle est dite “centrée réduite”.
Soit X une variable aléatoire (discrète ou continue) d’espérance mathématique E (X) et de variance σ2
X.
La variable aléatoire Y définie par Y = X − E (X) est dite variable aléatoire centrée associée à X, puisqu’on a :
E (Y ) = E (X − E (X)) = E (X) − E (X) = 0
La variable aléatoire Z définie par Z =
X − E (X)
σX
est dite variable aléatoire centrée réduite associée à X,
puisqu’on a :
E (Z) = E
µ
X − E (X)
σX
¶
=
1
σX
E (X − E (X)) = 0, et
V (Z) = V
µ
X − E (X)
σX
¶
=
1
σ2
X
V (X − E (X)) =
1
σ2
X
V (X) = 1
2 Fonction d’une variable aléatoire : Y = h (X)
Soit X une variable aléatoire, et soit h une fonction numérique définie sur X (Ω) . l’application Y = h◦X, définie
sur Ω est une variable aléatoire.
On dit que Y est une variable aléatoire fonction de la variable aléatoire X et on note Y = h (X) .
Le but de cette section consiste à montrer comment, à partir de la loi de probabilité de X, on peut déduire celle
de Y
2.1 Le cas d’une variable aléatoire discrète
Lorsque la v.a. X est une v.a. discrète, la variable Y = h (X) est elle même discrète et la détermination de sa
loi de probabilité à partir de celle de X ne présente en général pas de difficultés.
La détermination de la loi de Y se fait en deux étapes :
1 `ere
étape :
Déterminer l’ensemble des valeurs possibles de la variable aléatoire Y = h (X) , c.-à-d. Y (Ω) :
Y (Ω) = {yj ∈ R / yj = h(xi), xi ∈ X (Ω)}
Exemple : Soit X une v.a. discrète qui peut prendre les valeurs suivantes : X (Ω) = {−2, −1, 0, 1, 2, 3} et soit Y
la v.a. définie par :
( ) { }2, 1, 0, 1, 2, 3X Ω = − −
( ) 2 3Y h X X= = − ( )
2
Y h X X= =
( ) { }7, 5, 3, 1, 1, 3Y Ω = − − − −
h
( ) { }2, 1, 0, 1, 2, 3X Ω = − −
( ) { }0, 1, 4, 9Y Ω =
h
h bijective sur h non bijective sur( )X Ω ( )X Ω
2 `eme
étape :
Déterminer la probabilité associée à chacune des valeurs prises par la v.a. Y et ce en utilisant la propriété de
l’équivalence des événements :
15

16. ∀y ∈ Y (Ω) , P (Y = y) = P (h (X) = y) =
⎧
⎪⎨
⎪⎩
P
¡
X = h−1
(y)
¢
= P (X = x) si h est bijective
P
i
P (X = xi)
¯
¯
¯
¯
h(xi)=y
si h n’est pas bijective
Suite de l’exemple :
Supposons que la loi de probabilité de X est donnée par le tableau suivant :
X : −2 −1 0 1 2 3
Pi = P(X = xi) :
1
16
1
8
3
16
1
4
1
4
1
8
Pour Y = 2X − 3 Pour Y = X2
P (Y = −7) = P (2X − 3 = −7) = P (X = −2) =
1
16
P (Y = −5) = P (X = −1) =
1
8
P (Y = −3) = P (X = 0) =
3
16
P (Y = −1) = P (X = 1) =
1
4
P (Y = 1) = P (X = 2) =
1
4
P (Y = 3) = P (X = 3) =
1
8
P (Y = 0) = P (X = 0) =
3
16
P (Y = 1) = P
¡
X2
= 1
¢
= P (X = 1) + P (X = −1)
=
6
16
P (Y = 4) = P
¡
X2
= 4
¢
= P (X = 2) + P (X = −2)
=
5
16
P (Y = 9) = P (X = 3) =
2
16
Exercice :
Soit X une variable aléatoire discrète. Sa loi de probabilité est définie par :
X : −2 −1 0 1 2
Pi = P(X = xi) : 0, 1 0, 3 0, 4 k k
1. Déterminer k.
2. Calculer E (X) et V (X) .
3. Soit Y = 2X2
+ 3. Déterminer la loi de Y, E (Y ) et V (Y )
2.2 Le cas d’une variable aléatoire continue
Soit X une variable aléatoire continue de densité de probabilité fX et de fonction de répartition FX, et soit
Y = h(X) la variable aléatoire obtenue en appliquant la transformation h(.) à X.
On cherche à déterminer la densité de probabilité de Y, noté fY ainsi que sa fonction de répartition notée FY .
X X
X
f F
( ).h
? ?Y Y
Y
f F
2 cas sont à distinguer :
• le cas où h est strictement monotone sur X (Ω).
• le cas où h est non monotone sur X (Ω).
2.2.1 Cas d’une transformation strictement monotone
La fonction de répartition de Y s’écrit :
∀y ∈ R, on a FY (y) = P (Y < y)
16

17. La fonction h étant strictement monotone sur X (Ω) , elle admet donc une réciproque h−1
sur Y (Ω) . (h (X (Ω)) =
Y (Ω))
⇒ ∀y ∈ Y (Ω) , FY (y) = P (Y < y) = P (h(X) < y)
Or h peut être strictement croissante ou décroissante sur X (Ω) :
• si h est strictement croissante sur X (Ω) alors h−1
l’est aussi sur Y (Ω) et l’on peut écrire :
⇒ ∀y ∈ Y (Ω) , FY (y) = P (Y < y) = P (h(X) < y) = P
¡
X < h−1
(y)
¢
= FX
¡
h−1
(y)
¢
La fonction densité de Y, fY , s’obtient par dérivation de FY .
∀y ∈ Y (Ω) fY (y) = F0
Y (y) = F0
X
¡
h−1
(y)
¢
.
¡
h−1
(y)
¢0
= fX
¡
h−1
(y)
¢
.
∂
¡
h−1
(y)
¢
∂y
, avec
∂
¡
h−1
(y)
¢
∂y
> 0 (puisque h−1
est strictement %) et fX
¡
h−1
(y)
¢
≥ 0 (fonction densité)
y
Y y<
⎧⎪⎪⎪⎪⎪⎨
⎪⎪⎪⎪⎪⎩
Y
X
h(X)
h-1
(y)=x
( )1X h y−<
( )X Ω
( )Y Ω
Exemple :
Soit X une variable aléatoire continue de densité de probabilité :
fX(x) =
( 1
3
si 0 ≤ x ≤ 3
0 sinon
et soit Y une variable aléatoire fonction de X définie par : Y = h(X) = 2X. Déterminer la densité de probabilité
fY de Y ?
A partir de la densité de probabilité de X, on a X (Ω) = [0, 3] ⇒ Y (Ω) = h [X (Ω)] = [0, 6]
⇒ ∀y ∈ Y (Ω) = [0, 6] , FY (y) = P (Y < y) = P (h(X) < y) = P (2X < y) = P
⎛
⎜
⎜
⎝X <
y
2|{z}
h−1(y)
⎞
⎟
⎟
⎠ = FX
³y
2
´
La fonction densité de Y, fY , s’obtient par dérivation de FY :
∀y ∈ [0, 6] fY (y) = F0
Y (y) = fX
³y
2
´
.
µ
1
2
¶
Or fX
³y
2
´
=
( 1
3
si 0 ≤ y ≤ 6
0 sinon
, on a finalement :
fY (y) =
( 1
6
si 0 ≤ y ≤ 6
0 sinon
• si h est strictement décroissante sur X (Ω) alors h−1
l’est aussi sur Y (Ω) et l’on peut écrire :
17

18. ⇒ ∀y ∈ Y (Ω) , FY (y) = P (Y < y) = P (h(X) < y) = P
¡
X > h−1
(y)
¢
= 1 − P
¡
X ≤ h−1
(y)
¢
= 1 − FX
¡
h−1
(y)
¢
La fonction densité de Y, fY , s’obtient par dérivation de FY
∀y ∈ Y (Ω) fY (y) = F0
Y (y) = −F0
X
¡
h−1
(y)
¢
.
¡
h−1
(y)
¢0
= −fX
¡
h−1
(y)
¢
.
∂
¡
h−1
(y)
¢
∂y
, avec
∂
¡
h−1
(y)
¢
∂y
< 0 (puisque h−1
est strictement &)
y
Y y<
⎧⎪⎪⎪⎪⎪⎪⎨
⎪⎪⎪⎪⎪⎪⎩
Y
X
h(X)
h-1
(y)=x
( )1X h y−>
( )X Ω
( )Y Ω
Exemple :
Soit X une variable aléatoire continue de densité de probabilité :
fX(x) =
(
1
3
si 0 ≤ x ≤ 3
0 sinon
et soit Y une variable aléatoire fonction de X définie par : Y = h(X) = −2X. Déterminer la densité de
probabilité fY de Y ?
A partir de la densité de probabilité de X, on a X (Ω) = [0, 3] ⇒ Y (Ω) = h [X (Ω)] = [−6, 0]
⇒ ∀y ∈= [−6, 0] , FY (y) = P (Y < y) = P (h(X) < y) = P
⎛
⎜
⎜
⎝X > −
y
2|{z}
h−1(y)
⎞
⎟
⎟
⎠ = 1−P
³
X ≤ −
y
2
´
= 1−FX
³
−
y
2
´
La fonction densité de Y, fY , s’obtient par dérivation de FY :
∀y ∈= [−6, 0] fY (y) = F0
Y (y) =
h
1 − FX
³
−
y
2
´i0
= −fX
³
−
y
2
´
.
µ
−
1
2
¶
=
1
2
fX
³
−
y
2
´
Or fX
³
−
y
2
´
=
(
1
3
si − 6 ≤ y ≤ 0
0 sinon
, on a finalement :
fY (y) =
(
1
6
si − 6 ≤ y ≤ 0
0 sinon
D’une manière générale, si h est une fonction strictement monotone, alors la densité de probabilité de Y est
donnée par :
fY (y) =
⎧
⎪⎨
⎪⎩
fX
¡
h−1
(y)
¢
.
¯
¯
¯
¯
¯
∂
¡
h−1
(y)
¢
∂y
¯
¯
¯
¯
¯
∀y ∈ Y (Ω)
0 sinon
2.2.2 Cas d’une transformation non monotone
On se limitera ici aux cas des deux transformations h (X) = X2
et h (X) = |X|
18

19. • Cas de la transformation h (X) = X2
.
Soit X une variable aléatoire continue de densité de probabilité fX et de fonction de répartition FX, et soit
Y = h(X) = X2
une variable aléatoire fonction de X.
h(X) = X2
est une fonction non monotone sur R, elle est strictement croissante sur R+ et strictement
décroissante sur R−
Y y<
⎧⎪⎪⎪⎪⎪⎪⎨
⎪⎪⎪⎪⎪⎪⎩
Y
X
h(X)=X2
y yX− < <
y− y
Soit FY la fonction de répartition de Y :
⇒ ∀y ∈ Y (Ω) , FY (y) = P (Y < y) = P (h(X) < y) = P
¡
X2
< y
¢
= P
¡
|X| <
√
y
¢
= P
¡
−
√
y < X <
√
y
¢
= P
¡
X <
√
y
¢
− P
¡
X ≤ −
√
y
¢
= FX
¡√
y
¢
− FX
¡
−
√
y
¢
La fonction densité de Y, fY , s’obtient par dérivation de FY
∀y ∈ Y (Ω) {0} fY (y) = F0
Y (y) = F0
X
¡√
y
¢
.
¡√
y
¢0
− F0
X
¡
−
√
y
¢
.
¡
−
√
y
¢0
=
1
2
√
y
fX
¡√
y
¢
+
1
2
√
y
fX
¡
−
√
y
¢
=
1
2
√
y
£
fX
¡√
y
¢
+ fX
¡
−
√
y
¢¤
La densité de probabilité de Y est donc donnée par :
fY (y) =
⎧
⎨
⎩
1
2
√
y
£
fX
¡√
y
¢
+ fX
¡
−
√
y
¢¤
∀y ∈ Y (Ω) {0}
0 sinon
Exemple :
Soit X une variable aléatoire de densité de probabilité :
fX (x) =
(
1
2
si x ∈ [−1, 1]
0 sinon
Déterminer la densité de probabilité de Y = X2
. En déduire FY (y)
Solution :
On a X (Ω) = [−1, 1] =⇒ Y (Ω) = [0, 1]
⇒ ∀y ∈ [0, 1] FY (y) = P (Y < y) = P
¡
X2
< y
¢
= P
¡
−
√
y < X <
√
y
¢
= FX
¡√
y
¢
− FX
¡
−
√
y
¢
La fonction densité de Y, fY , s’obtient par dérivation de FY
⇒ ∀y ∈ ]0, 1] fY (y) = F0
Y (y) =
1
2
√
y
£
fX
¡√
y
¢
+ fX
¡
−
√
y
¢¤
On a y ∈ ]0, 1] ⇒
√
y ∈ ]0, 1] et −
√
y ∈ [−1, 0[ ⇒ fX
¡√
y
¢
= fX
¡
−
√
y
¢
=
1
2
⇒ ∀y ∈ ]0, 1] fY (y) =
1
2
√
y
19

20. La densité de probabilité de Y est donc donnée par :
fY (y) =
⎧
⎨
⎩
1
2
√
y
si y ∈ ]0, 1]
0 sinon
• Cas de la transformation h (X) = |X|
Soit X une variable aléatoire continue et soit Y la variable aléatoire définie par Y = h(X) = |X| .
h(X) = |X| est également une fonction non monotone sur R, elle est strictement croissante sur R+ et stricte-
ment décroissante sur R−
Y y<
⎧⎪⎪⎪⎪⎨
⎪⎪⎪⎪⎩
Y
X
y X y− < <
y− y
( )h X X=
Soit FY la fonction de répartition de Y :
⇒ ∀y ∈ Y (Ω) , FY (y) = P (Y < y) = P (h(X) < y) = P (|X| < y) = P (−y < X < y)
= P (X < y) − P (X ≤ −y)
= FX (y) − FX (−y)
La fonction densité de Y, fY , s’obtient par dérivation de FY
∀y ∈ Y (Ω) fY (y) = F0
Y (y) = F0
X (y) . (y)0
− F0
X (−y) . (−y)0
= fX (y) + fX (−y)
La densité de probabilité de Y est donc donnée par :
fY (y) =
½
fX (y) + fX (−y) ∀y ∈ Y (Ω)
0 sinon
Exemple :
Soit X une variable aléatoire de densité de probabilité :
fX (x) =
( 1
2
si x ∈ [−1, 1]
0 sinon
Déterminer la densité de probabilité de Y = |X| . En déduire FY (y)
Solution :
On a X (Ω) = [−1, 1] =⇒ Y (Ω) = [0, 1]
⇒ ∀y ∈ [0, 1] , FY (y) = P (Y < y) = P (|X| < y) = P (−y < X < y)
= P (X < y) − P (X ≤ −y)
= FX (y) − FX (−y)
La fonction densité de Y, fY , s’obtient par dérivation de FY
∀y ∈ [0, 1] , fY (y) = F0
Y (y) = fX (y) + fX (−y) =
1
2
+
1
2
= 1.
La densité de probabilité de Y est donc donnée par :
20

21. fY (y) =
½
1 si y ∈ [0, 1]
0 sinon
On a par définition FY (y) : R −→ [0, 1]
y 7−→ FY (y) = P (Y < y) =
R y
−∞
f(t)dt
Pour y < 0 ⇒ fY (y) = 0 ⇒ FY (y) =
R y
−∞
f(t)dt = 0
Pour 0 ≤ y < 1 ⇒ fY (y) = 1 ⇒ FY (y) =
R y
−∞
f(t)dt =
R 0
−∞
f(t)dt +
R y
0
f(t)dt =
R y
0
f(t)dt =
R y
0
1dt = [t]
y
0 = y
Pour y ≥ 1 ⇒ fY (y) = 0 ⇒ FY (y) =
R y
−∞
f(t)dt =
R 0
−∞
f(t)dt +
R 1
0
f(t)dt +
R y
1
f(t)dt =
R 1
0
f(t)dt = [t]
1
0 = 1
La fonction de répartition se Y est donc :
FY (y) =
⎧
⎨
⎩
0 si y < 0
y si 0 ≤ y < 1
1 si y ≥ 1
21

22. K&M http ://stat.fateback.com
Chapitre 2
Les lois de probabilités usuelles
Première partie
Les lois discrètes
1 La loi de Bernoulli : X Ã B (1, p)
1.1 Expérience de Bernoulli
Une expérience de Bernoulli est une expérience aléatoire simple au terme de laquelle 2 résultats seulement sont
possibles et mutuellement exclusifs. Ces deux résultats sont souvent désignés par l’appellation “succès” et “échec”.
Exemple : l’expérience qui consiste à tirer une boule dans une urne contenant des boules rouges et des boules
non rouges est une expérience de Bernoulli : Ω = {R, NR} .
1.2 Définition
Soit X la variable aléatoire associée à cette expérience. X prend la valeur 1 lorsque le résultat est un succès et
0 lorsque le résultat est un échec : X (Ω) = {0, 1} . Soit p la probabilité d’obtenir un succès et q = (1 − p) celle
d’obtenir un échec. La loi de probabilité de X est donnée par :
X : 0 1
P(X = x) : q = (1 − p) p
⇔ P (X = x) = px
(1 − p)1−x
, x ∈ {0, 1} .
La variable aléatoire ainsi définie est dite variable de Bernoulli et on note X Ã B (1, p) ou B (p)
Suite de l’exemple :
Si le nombre de boules rouges est égal au double de celui des boules non rouges, et si X prend la valeur 1
lorsque la boule tirée est rouge et 0 lorsque la boule est non rouge, alors la loi de probabilité de X est donnée par :
P (X = x) =
⎧
⎨
⎩
µ
2
3
¶x µ
1
3
¶1−x
si x ∈ {0, 1}
0 sinon
et on note X Ã B
µ
1,
2
3
¶
1.3 Paramètres descriptifs
1.3.1 Espérance mathématique
E (X) =
P
x∈X(Ω)
x.P (X = x) =
1P
x=0
x.px
. (1 − p)
1−x
= p
E (X) = p
Remarque : les moments non centrés d’ordre k (k ∈ N∗
) sont tous égals à p.
E
¡
Xk
¢
=
1P
x=0
xk
.px
. (1 − p)
1−x
= (1)
k
p1
. (1 − p)
0
= p ⇒ pour k = 2, E
¡
X2
¢
= p
1.3.2 Variance
V (X) = E
¡
X2
¢
− [E (X)]
2
= p − p2
= p (1 − p) = pq.
V (X) = p (1 − p) = pq
1

23. 1.4 Fonction génératrice des moments
MX (t) = E
¡
etX
¢
=
P
x∈X(Ω)
etx
P (X = x) =
1P
x=0
etx
px
(1 − p)
1−x
= (1 − p) + pet
= q + pet
.
MX (t) = q + pet
, ∀t ∈ R
Déduction de l’espérance et de la variance à partir de la F.G.M :
on a ∀k ∈ N∗
,
∂k
MX (t)
∂tk
= pet
⇒ E
¡
Xk
¢
=
∂k
MX (t)
∂tk
¯
¯
¯
¯
t=0
= p ⇒ E (X) = E
¡
X2
¢
= p.
⇒ V (X) = E
¡
X2
¢
− [E (X)]
2
= p − p2
= p (1 − p) = pq.
Tableau récapitulatif n◦
: 1
La loi de Bernoulli est la loi qui s’applique à des épreuves aléatoires
qui peuvent avoir seulement deux résultats possibles : “succès” et “échec”
X Ã B (1, p) ⇒ •X (Ω) = {0, 1}
•P (X = x) = px
(1 − p)1−x
x ∈ {0, 1}
•E (X) = p et V (X) = pq
•MX (t) = q + pet
, ∀t ∈ R
2

24. 2 La loi binomiale : X Ã B (n, p)
Si n expériences de Bernoulli identiques sont réalisées d’une manière indépendante, définissons les événements
Ai :
©
Xi = 1 pour la i`eme
expérience
ª
⇔
©
obtenir un succés à la i`eme
expérience
ª
, i = 1 . . . n. Soit X la variable
aléatoire définie par “le nombre total de succès dans les n expériences de Bernoulli”
Les événements {A1, A2, . . . , An} étant un ensemble d’événements indépendants, il sera donc simple de déduire
la distribution de probabilité de la variable aléatoire X .
X : “nombre total de succès dans les n expériences de Bernoulli” ⇒ X (Ω) = {0, 1, 2, . . . , n} .
L’événement {X = x} se réalise seulement si, parmi les n événements A1, A2, . . . , An, exactement x événements
se réalisent (et par suite nécessairement (n − x) ne se réalisent pas).
Un résultat particulier de la réalisation de ces n expériences peut être le suivant :
A1 ∩ A2 ∩ A3 ∩ . . . Ax
| {z }
x succés
∩ Ax+1 ∩ . . . ∩ An
| {z }
(n−x) échecs
dont la probabilité de réalisation est P
¡
A1 ∩ A2 ∩ A3 ∩ . . . Ax ∩ Ax+1 ∩ . . . ∩ An
¢
= px
(1 − p)n−x
Comme il existe {x
n façons différentes d’obtenir {X = x} . Nous en déduisons que :
P (X = x) = {x
npx
(1 − p)
n−x
= {x
npx
qn−x
2.1 Définition
On dit qu’une variable aléatoire X suit la loi binomiale de paramètres (n, p) et on note X Ã B (n, p) , si sa loi
de probabilité est donnée par :
P (X = x) =
½
{x
npx
qn−x
si x ∈ {0, 1, 2, . . . , n}
0 sinon
où n est un entier donné et p un réel tel que 0 ≤ p ≤ 1.
Remarque :
Le nom de cette loi provient du fait que les probabilités apparaissent comme les termes du développement du
binôme (p + q)n
, où n est le nombre d’expériences réalisées.
(p + q)
n
=
nP
x=0
{x
npx
qn−x
= P (X = 0) + P (X = 1) + · · · + P (X = n) = 1
2.2 Illustration par le schéma de l’urne1
Soit une urne qui contient des boules rouges (R) en proportion p et des boules non rouges (N) en proportion
(1 − p). On opère n tirages successifs, avec remise de la boule tirée après chaque tirage. Soit X la v.a. définie par
le nombre de boules rouges obtenues : X (Ω) = {0, 1, 2, . . . , n} . Puisqu’il y a remise, les épreuves successives (ici
les tirages) sont indépendantes et la proportion p (qui représente la probabilité de tirer une boule rouge lors d’un
tirage) reste constante.
Le schéma binomial est le suivant :
— Epreuve : on tire une boule
%
½
obtenir une boule rouge (succés) avec la probabilité p
Xi = 1
&
½
obtenir une boule non rouge (échec) avec la probabilité q = (1 − p)
Xi = 0
— L’épreuve est répétée n fois de suite avec la même probabilité de succès à chaque fois (les tirages sont avec
remise)
1 Schéma du tirage non exhaustif ou avec remise
3

25. p
q
p
q
R
N
p
qR
N
R
N
1 2 3RRR A A A⇔ ∩ ∩
1 2 3RRN A A A⇔ ∩ ∩
1 2 3RNR A A A⇔ ∩ ∩
1 2 3RNN A A A⇔ ∩ ∩
1 2 3NRR A A A⇔ ∩ ∩
1 2 3NRN A A A⇔ ∩ ∩
1 2 3
NNR A A A⇔ ∩ ∩
1 2 3NNN A A A⇔ ∩ ∩
p
qR
p
qR
N
R
N
p
q
R
N
RRR RR…
RRR RN…
RRR NR…
RRR NN…
p
q
N
p
qR
N
R
N
p
q
R
N
NNN RR…
NNN RN…
NNN NR…
NNN NN…
1 tirageer
2 tirageème
3 tirageème
tirageème
n
p
q
R
N
p
q
R
N
p
q
R
N
p
q
R
N
4

26. évenement élémentaire v.a. X Probabilité
1er
tirage : X Ã B (1, p)
R 1 P(X = 1) = P(A1) p
N 0 P(X = 0) = P(A1) q = (1 − p)
1
2`eme
tirage : X Ã B (2, p)
RR 2 P(X = 2) = P(A1 ∩ A2) p2
RN
NR
¾
1 P(X = 1) = P
£
(A1 ∩ A2) ∪ (A1 ∩ A2)
¤
2pq
NN 0 P(X = 0) = P(A1 ∩ A2) q2
1
3`eme
tirage : X Ã B (3, p)
RRR 3 P(X = 3) = P(A1 ∩ A2 ∩ A3) p3
RRN
RNR
NRR
⎫
⎬
⎭
2
P(X = 2) = P
£
(A1 ∩ A2 ∩ A3) ∪ (A1 ∩ A2 ∩ A3)
∪(A1 ∩ A2 ∩ A3)
¤ 3p2
q
RNN
NRN
NNR
⎫
⎬
⎭
1
P(X = 1) = P
£
(A1 ∩ A2 ∩ A3) ∪ (A1 ∩ A2 ∩ A3)
∪(A1 ∩ A2 ∩ A3)
¤ 3pq2
NNN 0 P(X = 0) = P(A1 ∩ A2 ∩ A3) q3
1
...
...
...
...
...
...
n`eme
tirage : X Ã B (n, p)
RRR . . . RR {n
n n P(X = n) = P(A1 ∩ A2 ∩ . . . ∩ An) pn
= {n
npn
q0
RRR . . . RN
RR . . . RNR
R . . . RNRR
...
NR . . . RRR
⎫
⎪⎪⎪⎪⎪⎬
⎪⎪⎪⎪⎪⎭
{n−1
n n − 1 P(X = n − 1) = {n−1
n pn−1
q
RR . . . RNN
...
)
{n−2
n n − 2 P(X = n − 2) = {n−2
n pn−2
q2
...
...
...
...
RR . . . R| {z }
x fois
N . . . N| {z }
n−x
...
⎫
⎪⎬
⎪⎭
{x
n x P(X = x) = {n−x
n pn−x
qx
...
...
...
...
NNN . . . NN {0
n 0 P(X = 0) = P(A1 ∩ A2 ∩ . . . ∩ An) {0
np0
qn
1
2.3 Paramètres descriptifs
2.3.1 Espérance mathématique
E(X) =
P
x∈X(Ω)
xP (X = x) =
nP
x=0
x{x
npx
(1 − p)n−x
= 0 +
nP
x=1
x{x
npx
(1 − p)n−x
Rappel : x{x
n = n{x−1
n−1
en effet x{x
n = x
n!
(n − x)!x!
=
n!
(n − x)! (x − 1)!
=
n (n − 1)!
((n − 1) − (x − 1))! (x − 1)!
= n{x−1
n−1.
5

27. ⇒ E(X) =
nP
x=1
n{x−1
n−1px
(1 − p)n−x
=
nP
x=1
n{x−1
n−1px−1
p (1 − p)(n−1)−(x−1)
= np
nP
x=1
{x−1
n−1px−1
(1 − p)(n−1)−(x−1)
posons y = x − 1
⇒ E(X) = np
n−1X
y=0
{y
n−1py
(1 − p)
(n−1)−y
| {z }
=1
;
n−1P
y=0
{y
n−1py
(1 − p)
(n−1)−y
=
P
y∈Y (Ω)
P(Y = y) où Y Ã B(n − 1, p)
⇒ E(X) = np (p + (1 − p))
n−1
= np
E(X) = np
2.3.2 Variance
V (X) = E (X − E (X))
2
= E
¡
X2
¢
− [E (X)]
2
or E
¡
X2
¢
=
P
x∈X(Ω)
x2
P (X = x) =
nP
x=0
x2
{x
npx
(1 − p)
n−x
= 0 +
nP
x=1
x2
{x
npx
(1 − p)n−x
=
nP
x=1
xn{x−1
n−1px−1
p (1 − p)(n−1)−(x−1)
= np
n−1P
y=0
(y + 1) {y
n−1py
(1 − p)(n−1)−y
, avec y = x − 1
= np
"
n−1P
y=0
y{y
n−1py
(1 − p)
(n−1)−y
+
n−1P
y=0
{y
n−1py
(1 − p)
(n−1)−y
#
n−1P
y=0
y{y
n−1py
(1 − p)(n−1)−y
= E(Y ) avec Y Ã B(n − 1, p) ⇒ E(Y ) = (n − 1) p
n−1P
y=0
{y
n−1py
(1 − p)(n−1)−y
= (p + (1 − p))n−1
= 1
⇒ E(X2
) = np [(n − 1) p + 1] = (np)
2
− np2
+ np
⇒ V (X) = E
¡
X2
¢
− [E (X)]2
= (np)2
− np2
+ np − (np)2
= np (1 − p) = npq
V (X) = npq
2.4 Fonction génératrice des moments
1`ere
méthode :
MX (t) = E
¡
etX
¢
=
P
x∈X(Ω)
etx
P (X = x) =
nP
x=0
etx
{x
npx
(1 − p)n−x
=
nP
x=0
{x
n (pet
)
x
(1 − p)n−x
= [pet
+ (1 − p)]
n
= [pet
+ q]
n
2`eme
méthode :
Une variable aléatoire qui suit la loi binomiale de paramètres (n, p) est une somme de n variables de Bernoulli
indépendantes de même paramètre p.
X Ã B(n, p) ⇔ X =
nP
i=1
Xi où les Xi sont indépendantes et Xi à B(1, p) ∀i : 1 . . . n.
Xi à B(1, p) ⇒ E (Xi) = p et V (Xi) = pq
Rappel :
E(
nP
i=1
Xi) =
nP
i=1
E (Xi) ∀Xi
V (
nP
i=1
Xi) =
nP
i=1
V (Xi)
E(
nQ
i=1
Xi) =
nQ
i=1
E (Xi)
⎫
⎪⎪⎬
⎪⎪⎭
seulement dans le cas où les Xi sont indépendantes
On a donc
E(X) = E(
nP
i=1
Xi) =
nP
i=1
E (Xi) =
nP
i=1
p = np
6

28. V (X) = V (
nP
i=1
Xi) =
nP
i=1
V (Xi) =
nP
i=1
pq = npq
MX (t) = E
¡
etX
¢
= E
³
et
Pn
i=1
Xi
´
= E
µ nQ
i=1
etXi
¶
=
nQ
i=1
E
¡
etXi
¢
puisque les Xi sont indépendantes
nQ
i=1
MXi (t) = [pet
+ q]
n
Déduction de l’espérance et de la variance à partir de la F.G.M :
∂MX (t)
∂t
= n (pet
) [pet
+ q]
n−1
⇒ E (X) =
∂MX (t)
∂t
¯
¯
¯
¯
t=0
= np
∂2
MX (t)
∂t2
= n
h
pet
[pet
+ q]
n−1
+ pet
h
(n − 1) pet
(pet
+ q)
n−2
ii
⇒ E
¡
X2
¢
=
∂2
MX (t)
∂t2
¯
¯
¯
¯
t=0
= n
h
p [p + q]
n−1
+ p
h
(n − 1) p (p + q)
n−2
ii
= n
£
p + (n − 1) p2
¤
⇒ V (X) = E
¡
X2
¢
− [E (X)]
2
= n
£
p + (n − 1) p2
¤
− (np)
2
= npq.
2.5 Stabilité de la loi binomiale par l’addition
Soient X1 et X2 deux variables aléatoires binomiales indépendantes telles que :
X1 Ã B(n1, p) et X2 Ã B(n2, p)
⇒ MX1 (t) = [pet
+ q]
n1
et MX2 (t) = [pet
+ q]
n2
Soit Y = X1+ X2 ⇒ MY (t) = E
¡
etY
¢
= E
¡
et(X1+X2)
¢
= E
¡
etX1
.etX2
¢
= E
¡
etX1
).E(etX2
¢
[X1etX2 sont indépendantes]
= MX1 (t) .MX2 (t) = [pet
+ q]
n1+n2
c’est la F.G.M. d’une binomiale (n1 + n2, p)
Conclusion :
Si k variables aléatoires indépendantes sont telles que Xi à B(ni, p) ∀i : 1 . . . k.
alors Y =
kP
i=1
Xi à B(
kP
i=1
ni, p)
2.6 Application
Une urne contient 5 boules dont 2 sont rouges (R) et les autres non rouges (N). On effectue 3 tirages indépendants
d’une boule chaque fois. Soit X le nombre de boules rouges extraites
1. Donner le support de X ainsi que sa loi de probabilité.
2. Calculer P(X = 2)
3. Calculer l’espérance et la variance de X
Solution :
1. Les tirages étant avec remise, on a X(Ω) = {0, 1, 2, 3}
p = P(tirer une boule rouge) =
2
5
et q = P(tirer une boule non rouge) =
3
5
X Ã B
µ
3,
2
5
¶
et on a P (X = x) =
⎧
⎨
⎩
{x
3
µ
2
5
¶x µ
3
5
¶3−x
si x ∈ {0, 1, 2, 3}
0 sinon
2. P(X = 2) = {2
3
µ
2
5
¶2 µ
3
5
¶
= 3 ×
µ
2
5
¶2 µ
3
5
¶
=
24
125
= 0, 192.
3. E (X) = np = 3 ×
2
5
=
6
5
et V (X) = 3 ×
2
5
×
3
5
=
18
25
7

29. Tableau récapitulatif n◦
: 2
La loi binomiale est utilisée lorsqu’on cherche à calculer la probabilité du nombre
de réalisations d’un événement à l’issue d’une successions de n essais indépendants
d’une épreuve aléatoire n’ayant que deux issues possibles, l’événement recherché
avec une probabilité p, l’autre avec une probabilité 1 − p.
X Ã B (n, p) ⇒ •X (Ω) = {0, 1, 2, . . . , n}
•P (X = x) = {x
npx
(1 − p)
n−x
x ∈ {0, 1, . . . , n}
•E (X) = np et V (X) = npq
•MX (t) = [q + pet
]
n
, ∀t ∈ R
X1 Ã B(n1, p) et X2 Ã B(n2, p) ⇒ X1 + X2 Ã B(n1 + n2, p)
Mots clès : tirage non exhaustif - tirages indépendants - tirages avec remise
8

30. 3 La loi de Poisson2
: X Ã P (λ)
La loi de Poisson s’appelle encore la loi des petites probabilités ou loi des phénomènes rares. Elle est utilisée
pour décrire le comportement d’événements dont les chances de réalisations sont faibles.
3.1 Définition
On dit qu’une variable aléatoire X, à valeurs dans N, suit une loi de Poisson de paramètre λ si, λ étant un réel
strictement positif, la loi de X est définie par :
P (X = x) =
⎧
⎨
⎩
e−λ
.λx
x!
x ∈ N
0 sinon
Une loi de Poisson étant parfaitement définie par le paramètre λ, on écrit alors : X Ã P(λ).
On vérifie que
P
x∈X(Ω)
P (X = x) =
∞P
x=0
e−λ
.λx
x!
= e−λ
∞P
x=0
λx
x!
= e−λ
.eλ
= 1.
3.2 Paramètres descriptifs
3.2.1 Espérance mathématique
E(X) =
P
x∈X(Ω)
x.P (X = x) =
∞P
x=0
xe−λ λx
x!
=
∞P
x=1
e−λ λx
(x − 1)!
= λe−λ
∞P
x=1
λx−1
(x − 1)!
= λe−λ
eλ
= λ.
E(X) = λ
Le paramètre λ s’interprète comme le taux moyen avec lequel un phénomène particulier apparaît.
3.2.2 Variance
V (X) = E
¡
X2
¢
− [E (X)]2
1`ere
méthode :
E
¡
X2
¢
=
P
x∈X(Ω)
x2
.P (X = x) =
∞P
x=0
x2
.e−λ λx
x!
= 0 +
∞P
x=1
x.e−λ λx
(x − 1)!
= e−λ
∞P
x=1
(x − 1 + 1) .
λx
(x − 1)!
= e−λ
∞P
x=1
(x − 1)
λx
(x − 1)!
+ e−λ
∞P
x=1
λx
(x − 1)!
= 0 + e−λ
∞P
x=2
λx
(x − 2)!
+ e−λ
∞P
x=1
λx
(x − 1)!
= λ2
e−λ
∞P
x=2
λx−2
(x − 2)!
+ λe−λ
∞P
x=1
λx−1
(x − 1)!
= λ2
e−λ
eλ
+ λe−λ
eλ
= λ2
+ λ
⇒ V (X) = E
¡
X2
¢
− [E (X)]
2
= λ2
+ λ − λ2
= λ
V (X) = λ
2`eme
méthode :
E
¡
X2
¢
=
∞P
x=0
x2
.e−λ λx
x!
=
∞P
x=0
[x(x − 1) + x] .e−λ λx
x!
=
∞P
x=0
x.(x − 1).e−λ λx
x!
+
∞P
x=0
x.e−λ λx
x!
=
∞P
x=2
x.(x − 1).e−λ λx
x!
+
∞P
x=1
x.e−λ λx
x!
= λ2
e−λ
∞P
x=2
λx−2
(x − 2)!
+ λe−λ
∞P
x=1
λx−1
(x − 1)!
= λ2
e−λ
eλ
+ λe−λ
eλ
= λ2
+ λ
2 Siméon D. Poisson, mathématicien français (1781-1840)
9

31. 3.3 Fonction génératrices des moments
MX (t) = E
¡
etX
¢
=
P
x∈X(Ω)
etx
P (X = x) =
∞P
x=0
etx
.
e−λ
.λx
x!
= e−λ
∞P
x=0
(λet
)
x
x!
= e−λ
eλet
= eλ(et
−1)
MX (t) = eλ(et
−1)
Déduction de l’espérance et de la variance à partir de la F.G.M :
∂MX (t)
∂t
= λet
eλ(et
−1) ⇒ E (X) =
∂MX (t)
∂t
¯
¯
¯
¯
t=0
= λ
∂2
MX (t)
∂t2
= λet
eλ(et
−1) + (λet
)
2
eλ(et
−1) = (λet
+ 1) λet
eλ(et
−1) ⇒ E
¡
X2
¢
=
∂2
MX (t)
∂t2
¯
¯
¯
¯
t=0
= λ2
+ λ
⇒ V (X) = E
¡
X2
¢
− [E (X)]2
= λ2
+ λ − λ2
= λ
3.4 Application
Une entreprise A a effectué une étude sur le nombre d’accidents de travail qui se sont produits durant les deux
dernières années. Ceci a permis d’établir que le taux moyen d’accidents de travail a été de 1, 6 accidents/jour.
En admettant que le nombre d’accidents de travail en une journée obéit à la loi de Poisson, quelle est la
probabilité d’observer plus de 2 accidents/jour ?
On a X : nombre d’accidents de travail par jour à P(1, 6)
P(X > 2) = 1 − P(X ≤ 2) = 1 − 0, 783 = 0, 217. (P(X ≤ 2) = 0, 783; voir table 4-1 : λ = 1, 6)
= 1 − P(X = 0) − P(X = 1) − P(X = 2)
= 1 − 0, 202 − 0, 323 − 0, 258 = 0, 217 (voir table 3-1)
3.5 Stabilité de la loi de Poisson par addition
Soient X1 et X2 deux variables aléatoires de Poisson de paramètres respectivement λ1 et λ2
c.-à-d. X1 Ã P(λ1) et X2 Ã P(λ2)
si X1 et X2 sont indépendantes alors la v.a. Y = X1 + X2 Ã P(λ1 + λ2).
En effet :
MY (t) = E
¡
etY
¢
= E
¡
et(X1+X2)
¢
= E
¡
etX1
.etX2
¢
= E
¡
etX1
).E(etX2
¢
[X1etX2 sont indépendantes]
= MX1 (t) .MX2 (t) = eλ1(et
−1).eλ2(et
−1) = e(λ1+λ2)[et
−1]
e(λ1+λ2)[et
−1] est la F.G.M. d’une variable de Poisson de paramètre (λ1 + λ2)
d’où Y = X1 + X2 Ã P(λ1 + λ2).
3.6 Approximation de la loi binomiale par la loi de Poisson
On utilisera, le plus souvent, la loi de Poisson comme approximation d’une loi binomiale.
Supposons que les conditions d’application de la loi binomiale sont réalisées mais que toutefois le nombre
d’épreuves (la taille d’échantillon n) est très grand, que p est faible, de telle façon que np reste petit par rapport à
n, alors on peut approximer la loi binomiale de paramètres (n, p) par une loi de Poisson de paramètre (λ = np) .
En pratique l’approximation est valable si :
n ≥ 30, p ≤ 0, 1.
Démonstration : (Facultative)
X Ã B (n, p) ⇒ MX(t) = [pet
+ (1 − p)]
n
Y Ã P(λ) ⇒ MY (t) = eλ(et
−1)
Posons λ = np
MX(t) = [pet
+ (1 − p)]
n
=
∙
1 +
1
n
(et
− 1)np
¸n
=
∙
1 +
λ(et
− 1)
n
¸n
lim
n→∞
MX(t) = lim
n→∞
∙
1 +
λ(et
− 1)
n
¸n
= eλ(et
−1)
= MY (t).
10

32. 4 La loi géométrique (ou loi binomiale négative d’ordre 1)
Soit une expérience de Bernoulli comportant deux résultats possibles : un "succès" avec une probabilité p et
un "échec" avec une probabilité q = (1 − p). On répète l’expérience jusqu’à l’apparition du premier "succès" (le
nombre de répétition n’est pas fixé en avance, il est conditionné par l’apparition de "succès" pour la première fois).
Soit X la variable aléatoire associée à cette expérience et définie par le nombre de fois qu’il faut répéter l’expérience
pour obtenir un premier "succès". L’ensemble des valeurs de X est : X (Ω) = {1, 2, 3, . . .} = N∗
.
La probabilité d’avoir recours à X = x répétitions de l’épreuve élémentaire de Bernoulli pour observer la
première apparition de "succès" est donnée par la loi géométrique dont l’expression est :
P(X = x) = (1 − p)
x−1
.p
En effet :
1. Chaque expérience peut entraîner l’observation d’un événement A : ”succ`es” ou de son contraire A : ”´echec”.
2. La probabilité de A, notée p, est la même pour chaque expérience. (tirage avec remise s’il s’agit d’un modèle
de l’urne).
3. Le résultat d’une expérience est indépendant des résultats des autres expériences.
On note Ax l’événement : "A se réalise à la x`eme
expérience".
P(X = x) = P(d’observer la première apparition de "succès" à la x`eme
expérience) = P(A1∩A2∩. . .∩Ax−1∩Ax).
L’indépendance des événements permet d’ecrire :
P(X = x) = P
¡
A1
¢
.P
¡
A2
¢
. . . P
¡
Ax−1
¢
.P(Ax) = (1 − p)
x−1
.p
4.1 Définition
On dit qu’une variable aléatoire X, à valeurs dans N∗
, suit une loi géométrique de paramètre p (0 < p < 1), si
sa loi de probabilité est définie par :
P(X = x) =
½
(1 − p)
x−1
.p si x ∈ N∗
0 sinon
et on note X Ã G (p) ou X Ã B (1, p) .
La variable aléatoire X ainsi définie, est dite variable d’attente du premier "succès".
On peut vérifier que
∞P
x=1
P(X = x) = 1
On a
∞P
x=1
P(X = x) =
∞P
x=1
(1 − p)
x−1
.p = p
∞P
x=1
(1 − p)
x−1
= p
µ
lim
n→∞
nP
x=1
(1 − p)
x−1
¶
= p
³
lim
n→∞
³
1 + (1 − p)1
+ · · · + (1 − p)n−1
´´
= p
µ
lim
n→∞
µ
1 − (1 − p)n
1 − (1 − p)
¶¶
= p
µ
1
1 − (1 − p)
¶
(0 < 1 − p < 1)
= p
µ
1
p
¶
= 1
Il ne faut jamais oublier que
∞P
n=0
qn
converge vers
1
1 − q
si et seulement si |q| < 1
4.2 Paramètres descriptifs
Rappel mathématique :
si |q| < 1, on a
∞P
n=0
qn
=
1
1 − q
⇒
µ ∞P
n=0
qn
¶0
=
µ
1
1 − q
¶0
=
1
(1 − q)
2
or
∞P
n=0
qn
= 1 +
∞P
n=1
qn
⇒
µ ∞P
n=0
qn
¶0
=
µ
1 +
∞P
n=1
qn
¶0
=
µ ∞P
n=1
qn
¶0
=
∞P
n=1
(qn
)0
=
∞P
n=1
nqn−1
11

33. ce qui nous permet d’ecrire :
∞P
n=1
nqn−1
=
1
(1 − q)2 si |q| < 1 (A)
De même,
si |q| < 1, on a
∞P
n=0
qn
=
1
1 − q
⇒
µ ∞P
n=0
qn
¶00
=
µ
1
1 − q
¶00
=
2
(1 − q)3
or
∞P
n=0
qn
= 1 + q +
∞P
n=2
qn
⇒
µ ∞P
n=0
qn
¶00
=
µ
1 + q +
∞P
n=2
qn
¶00
=
µ ∞P
n=2
qn
¶00
=
∞P
n=2
(qn
)00
=
∞P
n=2
n (n − 1) qn−2
et on a
∞P
n=1
n (n − 1) qn−2
=
2
(1 − q)3 si |q| < 1 (B)
4.2.1 Espérance mathématique
E(X) =
P
x∈X(Ω)
x.P (X = x) =
∞P
x=1
x.p. (1 − p)
x−1
= p
∞P
x=1
x (1 − p)
x−1
or d’après (A), on a
∞P
x=1
x (1 − p)
x−1
=
1
(1 − (1 − p))
2 =
1
p2
⇒ E(X) =
1
p
4.2.2 Variance
V (X) = E
¡
X2
¢
− [E (X)]2
E
¡
X2
¢
=
P
x∈X(Ω)
x2
.P (X = x) =
∞P
x=1
x2
. (1 − p)
x−1
p =
∞P
x=1
(x (x − 1) + x) . (1 − p)
x−1
p
= p
∞P
x=1
x (x − 1) . (1 − p)
x−1
+
∞P
x=1
x (1 − p)
x−1
p
= p
∞P
x=1
x (x − 1) . (1 − p)
x−1
+ E(X)
= 0 + p (1 − p)
∞P
x=2
x (x − 1) . (1 − p)
x−2
+
1
p
or d’après (B), on a
∞P
x=2
x (x − 1) (1 − p)
x−2
=
2
(1 − (1 − p))
3 =
2
p3
.
⇒ E
¡
X2
¢
= p (1 − p)
2
p3
+
1
p
=
2 (1 − p) + p
p2
⇒ V (X) =
2 (1 − p) + p
p2
−
1
p2
=
(1 − p)
p2
=
q
p2
V (X) =
(1 − p)
p2
=
q
p2
4.3 Fonction génératrice des moments
MX(t) = E(etX
) =
∞P
x=1
etx
. (1 − p)
x−1
.p = pet
∞P
x=1
[et
(1 − p)]
x−1
= pet
∞P
y=0
(qet
)
y
avec (y = x − 1)
= pet 1
1 − qet
si qet
< 1
⇔ MX(t) =
pet
1 − qet
si t < Log
µ
1
q
¶
(on vérifie bien que t = 0 ∈
¸
−∞, Log
µ
1
q
¶∙
, puisque 0 < q < 1 ⇔
1
q
>
1 ⇔ Log
µ
1
q
¶
> 0).
On peut donc déduire l’espérance et la variance à partir de la fonction génératrice des moments (prenez le temps
de le faire !).
12

34. 5 La loi binomiale négative d’ordre k : X Ã B (k, p)
On se place dans les conditions d’une loi géométrique, seulement on s’intéresse à présent à répéter l’épreuve
élémentaire jusqu’à l’obtention du ki`eme
"succès". Soit X la variable aléatoire définie par le nombre de répétitions
qu’il faut effectuer pour obtenir k succès. Pour obtenir k succès, on doit avoir recours à au moins k répétitions de
l’épreuve élémentaire. l’ensemble des observables de X est donc X (Ω) = {k, k + 1, . . .}
l’événement {X = x} se réalise si et seulement si :
— (k − 1) "succès" ont été obtenu, avant la répétition numéro x (c.-à-d. en (x − 1) répétitions)
— le ki`eme
"succès" a été obtenu à la répétition numéro x
et on peut écrire :
P(X = x) = P(d’avoir recours à x répétitions jusqu’à l’apparition du ki`eme
"succès")
= P(d’obtenir (k − 1) "succès" en (x − 1) répétitions) × P(d’obtenir "succès" à la x`eme
répétition)
= P(d’obtenir (k − 1) "succès" en (x − 1) répétitions) × p
= P(Y = k − 1) × p, avec Y Ã B (x − 1, p) , y ∈ {0, 1, . . . , x − 1}
= {k−1
x−1pk−1
(1 − p)
x−k
× p = {k−1
x−1pk
(1 − p)
x−k
5.1 Définition
On dit qu’une variable aléatoire X suit la loi binomiale négative d’ordre k et on note X Ã B (k, p), si sa loi de
probabilité est donnée par :
P (X = x) =
½
{k−1
x−1pk
(1 − p)x−k
∀ x ∈ {k, k + 1, . . .}
0 sinon
5.2 Paramètres descriptifs
5.2.1 Espérance mathématique
E(X) =
P
x∈X(Ω)
x.P (X = x) =
∞P
x=k
x.{k−1
x−1pk
(1 − p)x−k
=
∞P
x=k
x.
(x − 1)!
(x − k)! (k − 1)!
pk
(1 − p)
x−k
5. MY (t) = E(etY
) =
∞P
y=r
ety
.{r−1
y−1pr
(1 − p)y−r
= pr
∞P
y=r
etr
et(y−r)
.{r−1
y−1 (1 − p)y−r
= etr
pr
∞P
y=r
{r−1
y−1 [(1 − p) et
]
y−r
= etr
pr
[1 − (1 − p) et
]
−r
si (1 − p) et
< 1
=
∙
pet
1 − (1 − p) et
¸r
si t < Log
∙
1
(1 − p)
¸
∂MY (t)
∂t
= r
∙
pet
1 − (1 − p) et
¸r−1
"
pet
(1 − (1 − p) et
) + pet
((1 − p) et
)
(1 − (1 − p) et)2
#
E (X) =
∂MX (t)
∂t
¯
¯
¯
¯
t=0
= r
∙
p
p
¸r−1 ∙
p2
+ p − p2
p2
¸
=
r
p
.
13

35. Deuxième partie
Les lois continues
1 La loi uniforme continue (ou loi rectangulaire) : X Ã U ([a, b])
1.1 Définition
Soit X une variable aléatoire continue. Sa distribution est dite uniforme sur [a, b] (a < b), si sa densité de
probabilité est constante sur cet intervalle avec :
f(x) =
( 1
b − a
si x ∈ [a, b]
0 sinon
et on écrit X Ã U ([a, b])
• Graphiquement, on a l’allure suivante :
( )f x
1
b a−
a b
On vérifie que
R +∞
−∞
f(x)dx =
R b
a
1
b − a
dx =
1
b − a
[x]b
a =
b − a
b − a
= 1
• L’aire comprise entre la courbe de f(x) et l’axe des abscisses n’est autre que la surface du rectangle de base (a, b)
et de hauteur
1
b − a
, d’où l’appellation de loi rectangulaire.
• Soient c et d deux réel tels que a < c < d < b, alors P(c < X < d) =
R d
c
f(x)dx =
d − c
b − a
( )f x
1
b a−
a bc d
( )P c X d< <
1.2 Fonction de répartition
F : R −→ [0, 1]
x 7−→ F (x) = P (X < x) =
R x
−∞
f(t)dt
avec f(t) =
( 1
b − a
si t ∈ [a, b]
0 sinon
14

36. si x < a ⇒ F (x) =
R x
−∞
f(t)dt = 0
si a ≤ x ≤ b ⇒ F (x) =
R x
−∞
f(t)dt =
R a
−∞
f(t)dt +
R x
a
f(t)dt =
1
b − a
R x
a
dt =
x − a
b − a
si x > b ⇒ F (x) =
R x
−∞
f(t)dt =
R a
−∞
f(t)dt +
R b
a
f(t)dt +
R x
b
f(t)dt =
1
b − a
R b
a
dt = 1
⇒ F(x) =



0 si x < a
x − a
b − a
si a ≤ x ≤ b
1 si x > b
( )F x
2
a b+a b
1
0,5
• La médiane est la valeur de x telle que F(x) = 0, 5
F(x) = 0, 5 ⇒
x − a
b − a
= 0, 5 ⇒ x =
1
2
(b − a) + a =
a + b
2
⇒ Me =
a + b
2
1.3 Paramètres descriptifs
1.3.1 Espérance mathématique
E(X) =
R +∞
−∞
xf(x)dx =
1
b − a
R b
a
xdx =
1
b − a
·
x2
2
¸b
a
=
b2
− a2
2 (b − a)
=
a + b
2
E(X) =
a + b
2
1.3.2 Variance
V (X) = E(X2
) − [E(X)]
2
or E(X2
) =
R +∞
−∞
x2
f(x)dx =
1
b − a
R b
a
x2
dx =
1
b − a
·
x3
3
¸b
a
=
b3
− a3
3 (b − a)
=
(b − a)
¡
a2
+ b2
+ ab
¢
3 (b − a)
=
¡
a2
+ b2
+ ab
¢
3
⇒ V (X) =
¡
a2
+ b2
+ ab
¢
3
−
(a + b)
4
2
=
(b − a)2
12
V (X) =
(b − a)2
12
1.4 Fonction génératrice des moments
MX (t) = E
¡
etX
¢
=
R +∞
−∞
etx
f(x)dx =
1
b − a
R b
a
etx
dx =
1
b − a
·
etx
t
¸b
a
=
etb
− eta
t (b − a)
si t 6= 0
⇒ MX (t) =



etb
− eta
t (b − a)
si t 6= 0
1 sinon
• Déduction de l’espérance à partir de la fonction génératrice des moments (facultative) :
15

37. ∂MX (t)
∂t
=
¡
betb
− aeta
¢
(t (b − a)) − (b − a)
¡
etb
− eta
¢
t2 (b − a)2
=
¡
betb
− aeta
¢
t (b − a)
−
¡
etb
− eta
¢
t2 (b − a)
on sait que eta
=
∞P
x=0
(ta)x
x!
= 1 + ta +
(ta)2
2!
+
∞P
x=3
(ta)x
x!
etb
=
∞P
x=0
(tb)
x
x!
= 1 + tb +
(tb)
2
2!
+
∞P
x=3
(tb)
x
x!
⇒ etb
− eta
= t (b − a) +
t2
¡
b2
− a2
¢
2
+
∞P
x=3
tx
(bx
− ax
)
x!
⇒
etb
− eta
t2 (b − a)
=
1
t
+
b + a
2
+
∞P
x=3
tx−2
(bx
− ax
)
(b − a) x!
de même, on a aeta
= a + ta2
+
∞P
x=2
tx
ax+1
x!
betb
= b + tb2
+
∞P
x=2
tx
bx+1
x!
⇒ betb
− aeta
= (b − a) + t
¡
b2
− a2
¢
+
∞P
x=2
tx
¡
bx+1
− ax+1
¢
x!
⇒
betb
− aeta
t (b − a)
=
1
t
+ (b + a) +
∞P
x=2
tx−1
¡
bx+1
− ax+1
¢
(b − a) x!
⇒
∂MX (t)
∂t
=
¡
betb
− aeta
¢
t (b − a)
−
¡
etb
− eta
¢
t2 (b − a)
=
(b + a)
2
+
∞P
x=2
tx−1
¡
bx+1
− ax+1
¢
(b − a) x!
−
∞P
x=3
tx−2
(bx
− ax
)
(b − a) x!
⇒ E(X) = lim
t→0
∂MX (t)
∂t
=
(b + a)
2
2 La loi exponentielle : X Ã ξ (θ)
2.1 Définition
On dit qu’une variable aléatoire X suit une loi exponentielle de paramètre θ > 0, lorsque sa densité de probabilité
est définie par :
f(x) =
½
θe−θx
si x ≥ 0
0 sinon
et on note X Ã ξ (θ)
On vérifie que
R +∞
−∞
f(x)dx =
R +∞
0
θe−θx
dx =
£
−e−θx
¤+∞
0
= 1.
2.2 Fonction de répartition
F : R −→ [0, 1]
x 7−→ F (x) = P (X < x) =
R x
−∞
f(t)dt avec f(t) =
½
θe−θt
si t ≥ 0
0 sinon
si x < 0 ⇒ F (x) =
R x
−∞
f(t)dt = 0
si x ≥ 0 ⇒ F (x) =
R x
−∞
f(t)dt =
R x
0
θe−θt
dt =
£
−e−θt
¤x
0
= 1 − e−θx
⇒ F(x) =
½
0 si x < 0
1 − e−θx
si x ≥ 0
On vérifie que lim
x→+∞
F(x) = lim
x→+∞
¡
1 − e−θx
¢
= 1
• La médiane est telle que F(Me) = 0, 5
F(Me) = 0, 5 ⇔ 1 − e−θMe
= 0, 5 ⇔ e−θMe
= 0, 5 ⇔ Me = −
1
θ
Log (0, 5)
16

38. 2.3 Paramètres descriptifs
2.3.1 Espérance mathématique
E(X) =
R +∞
−∞
xf(x)dx =
R +∞
0
xθe−θx
dx
en intégrant par partie : u(x) = x ⇒ u0
(x) = 1
v0
(x) = θe−θx
⇒ v(x) = −e−θx
⇒ E(X) =
R +∞
0
xθe−θx
dx =
£
−xe−θx
¤+∞
0
+
R +∞
0
e−θx
dx =
·
−
1
θ
e−θx
¸+∞
0
=
1
θ
E(X) =
1
θ
2.3.2 Variance
V (X) = E(X2
) − [E(X)]
2
avec E(X2
) =
R +∞
−∞
x2
f(x)dx =
R +∞
0
x2
θe−θx
dx
en intégrant par partie : u(x) = x2
⇒ u0
(x) = 2x
v0
(x) = θe−θx
⇒ v(x) = −e−θx
⇒ E(X2
) =
R +∞
0
x2
θe−θx
dx =
£
−x2
e−θx
¤+∞
0
+ 2
R +∞
0
xe−θx
dx =
2
θ
R +∞
0
xθe−θx
dx =
2
θ
E(X) =
2
θ2
⇒ V (X) =
2
θ2 −
1
θ2 =
1
θ2
V (X) =
1
θ2
Remarque :
Le moment non centré d’ordre k est défini par :
E(Xk
) =
R +∞
−∞
xk
f(x)dx =
R +∞
0
xk
θe−θx
dx = θ
R +∞
0
xk
e−θx
dx = θIk
en intégrant par partie : u(x) = xk
⇒ u0
(x) = kxk−1
v0
(x) = e−θx
⇒ v(x) = −
1
θ
e−θx
⇒ Ik =
·
−
xk
θ
e−θx
¸+∞
0
+
k
θ
R +∞
0
xk−1
e−θx
dx =
k
θ
Ik−1 ⇒ Ik =
k
θ
Ik−1 ∀k ∈ N∗
⇒
I1 =
1
θ
I0
I2 =
2
θ
I1
...
Ik−1 =
k − 1
θ
Ik−2
Ik =
k
θ
Ik−1



⇒ Ik =
k
θ
×
k − 1
θ
×· · ·
2
θ
×
1
θ
×I0 =
k!
θk
I0 avec I0 =
R +∞
0
e−θx
dx =
·
−
1
θ
e−θx
¸+∞
0
=
1
θ
⇒ Ik =
k!
θk
I0 =
k!
θk+1
⇒ E(Xk
) = θIk =
k!
θk
Implication : pour k = 1 on a E(X) =
1
θ
pour k = 2 on a E(X2
) =
2
θ2
2.4 Fonction génératrice des moments
MX (t) = E
¡
etX
¢
=
R +∞
−∞
etx
f(x)dx =
R +∞
0
etx
θe−θx
dx = θ
R +∞
0
e(t−θ)x
dx = θ
·
1
t − θ
e(t−θ)x
¸+∞
0
=
θ
θ − t
si
t < θ
Déduction de l’espérance et de la variance à partir de la F.G.M :
•
∂MX (t)
∂t
=
θ
(θ − t)
2 ⇒ E (X) =
∂MX (t)
∂t
¯
¯
¯
¯
t=0
=
1
θ
17

39. •
∂2
MX (t)
∂t2
=
2θ
(θ − t)3 ⇒ E
¡
X2
¢
=
∂2
MX (t)
∂t2
¯
¯
¯
¯
t=0
=
2
θ2 ⇒ V (X) = E(X2
) − [E(X)]2
=
1
θ2
Remarque : La loi exponentielle n’est pas stable par l’addition
Soient X1 et X2 deux variables aléatoires indépendantes telles que : X1 Ã ξ (θ1) et X2 Ã ξ (θ2)
si Y = X1 + X2, nous n’avons pas Y Ã ξ (θ1 + θ2) c.-à-d. nous n’avons pas MY (t) =
(θ1 + θ2)
(θ1 + θ2) − t
MY (t) = E
¡
etY
¢
= E
¡
et(X1+X2)
¢
= E
¡
etX1
¢
E
¡
etX2
¢
= MX1 (t) MX2 (t) =
θ1
θ1 − t
×
θ2
θ2 − t
=
θ1θ2
(θ1 − t) (θ2 − t)
2.5 Application
Soient X et Y deux variables aléatoires tells que X Ã U ([−3, −1]) et Y Ã ξ (θ) .
Trouver θ, sachant que V (X) = V (Y ).
Solution :
X Ã U ([−3, −1]) ⇒ V (X) =
(−1 + 3)2
12
=
1
3
Y Ã ξ (θ) ⇒ V (Y ) =
1
θ2
V (X) = V (Y ) ⇔
1
θ2 =
1
3
⇔ θ2
= 3 ⇔ |θ| =
√
3 ⇒ θ =
√
3 (θ = −
√
3 est à rejeter car θ > 0 par hypothèse).
3 La loi gamma : X Ã γ (α, θ)
3.1 La fonction Gamma
3.1.1 Définition
La fonction Gamma est définie sur R∗
+ et à valeurs dans R+ par :
Γ (α) =
Z +∞
0
tα−1
e−t
dt
3.1.2 Propriétés de la fonction Gamma
1. ∀α ∈ R∗
+ on a Γ (α + 1) = αΓ (α) .
En effet, Γ (α + 1) =
R +∞
0
tα
e−t
dt
en intégrant par partie : u(t) = tα
⇒ u0
(t) = αtα−1
v0
(x) = e−t
⇒ v(x) = −e−t
on obtient : Γ (α + 1) =
R +∞
0
tα
e−t
dt = [−tα
e−t
]
+∞
0 +
R +∞
0
αtα−1
e−t
dt
= α
R +∞
0
tα−1
e−t
dt = αΓ (α)
Implication : ∀n ∈ N∗
Γ (n) = (n − 1)!
∀α ∈ R∗
+ on a Γ (α + 1) = αΓ (α)
pour α = 1 ⇒ Γ (2) = 1 × Γ (1)
pour α = 2 ⇒ Γ (3) = 2 × Γ (2) = 2 × 1 × Γ (1)
...
pour α = n − 1 ⇒ Γ (n) = (n − 1) × Γ (n − 1) = (n − 1) × (n − 2) × · · · × 2 × 1 × Γ (1)
= (n − 1)! × Γ (1)
or Γ (1) =
R +∞
0
e−t
dt = [−e−t
]
+∞
0 = 1 (e−t
n’est autre que la densité d’une ξ (1))
∀n ∈ N∗
Γ (n) = (n − 1)!
2. Γ
µ
1
2
¶
=
R +∞
0
t
−1
2 e−t
dt =
√
Π
Démonstration (facultative)
On sait que Γ (α) =
R +∞
0
tα−1
e−t
dt. En posant x =
√
t ⇒ x2
= t ⇒ dt = 2xdx, on a :
18

40. Γ (α) =
R +∞
0
tα−1
e−t
dt =
R +∞
0
x2(α−1)
e−x2
2xdx = 2
R +∞
0
x2α−1
e−x2
dx
Montrons que
·
Γ
µ
1
2
¶¸2
= Π
·
Γ
µ
1
2
¶¸2
= 4
hR +∞
0
e−x2
dx
i2
= 4
hR +∞
0
e−x2
dx
i hR +∞
0
e−x2
dx
i
les variables d’intégration étant des variables muettes, changer leurs noms est tout à fait permis :
·
Γ
µ
1
2
¶¸2
= 4
R +∞
0
e−u2
du
R +∞
0
e−v2
dv
= 4
R +∞
0
R +∞
0
e−(u2
+v2
)dudv
Le passage aux coordonnées polaires donne :
u = r cos θ v = r sin θ
u2
+ v2
= r2
et dudv = rdrdθ
u > 0, v > 0 ⇒ r > 0 et 0 < θ <
Π
2
·
Γ
µ
1
2
¶¸2
= 4
R +∞
0
R Π
2
0
re−r2
drdθ = 4
R +∞
0
h
re−r2 R Π
2
0
dθ
i
dr
= 4
R +∞
0
Π
2
re−r2
dr
= 2Π
µ
−1
2
¶
R +∞
0
−2re−r2
dr
= −Π
h
e−r2
i+∞
0
= Π
⇒ Γ
µ
1
2
¶
=
√
Π
3.2 La loi gamma
3.2.1 Définition
Soit X une variable aléatoire continue. On dit que X suit une loi gamma de paramètres (α, θ) α > 0 et θ > 0 si
et seulement si elle admet pour densité la fonction suivante :
f(x) =



θα
Γ (α)
xα−1
e−θx
si x > 0
0 sinon
et on écrit X Ã γ (α, θ)
On vérifie que
R +∞
−∞
f(x)dx = 1,
R +∞
0
θα
Γ (α)
xα−1
e−θx
dx =
R +∞
0
θ
Γ (α)
(θx)
α−1
e−θx
dx
=
1
Γ (α)
R +∞
0
tα−1
e−t
dt
=
1
Γ (α)
Γ (α) = 1
, en posant t = θx ⇒ dt = θdx
Remarque 1 :
On a
R +∞
0
θα
Γ (α)
xα−1
e−θx
dx = 1 ⇒
R +∞
0
xα−1
e−θx
dx =
Γ (α)
θα
Remarque 2 :
X Ã γ (1, θ) ⇒ f(x) =
θ
Γ (1)
x1−1
e−θx
=
θe−θx
Γ (1)
= θe−θx
c’est la densité de probabilité d’une exponentielle de
paramètre θ. Si α = 1, la distribution gamma se réduit à une distribution exponentielle γ (1, θ) ≡ ξ (θ)
19

41. 3.2.2 Paramètres descriptifs
Espérance mathématique
E(X) =
R +∞
−∞
xf(x)dx =
R +∞
0
x
θα
Γ (α)
xα−1
e−θx
dx =
θα
Γ (α)
R +∞
0
xα
e−θx
dx =
θα
Γ (α)
Γ (α + 1)
θα+1 =
α
θ
E(X) =
α
θ
Variance
V (X) = E(X2
) − [E(X)]
2
E(X2
) =
R +∞
−∞
x2
f(x)dx =
R +∞
0
x2 θα
Γ (α)
xα−1
e−θx
dx =
θα
Γ (α)
R +∞
0
xα+1
e−θx
dx =
θα
Γ (α)
Γ (α + 2)
θα+2
=
θα
Γ (α)
α (α + 1) Γ (α)
θα+2
=
α (α + 1)
θ2
V (X) =
α (α + 1)
θ2 −
³α
θ
´2
=
α
θ2
V (X) =
α
θ2
3.2.3 Fonction génératrice des moments
MX (t) = E
¡
etX
¢
=
R +∞
−∞
etx
f(x)dx =
R +∞
0
etx θα
Γ (α)
xα−1
e−θx
dx
=
θα
Γ (α)
R +∞
0
xα−1
e(t−θ)x
dx
=
θα
Γ (α)
R +∞
0
xα−1
e−(θ−t)x
dx
=
θα
Γ (α)
Γ (α)
(θ − t)α =
·
θ
(θ − t)
¸α
avec θ > t
Remarque : pour α = 1, on retrouve la fonction génératrice des moments d’une loi exponentielle ξ (θ).
Déduction de l’espérance et de la variance à partir de la fonction génératrice des moments :
On a : MX (t) =
·
θ
(θ − t)
¸α
•
∂MX (t)
∂t
= α
θ
(θ − t)2
·
θ
(θ − t)
¸α−1
= α
θα
(θ − t)α+1 ⇒ E (X) =
∂MX (t)
∂t
¯
¯
¯
¯
t=0
=
α
θ
•
∂2
MX (t)
∂t2
=
"
α
θα
(θ − t)
α+1
#0
= αθα
h
(θ − t)
−α−1
i0
= αθα
h
(−α − 1) (−1) (θ − t)
−α−2
i
= α (α + 1)
"
θα
(θ − t)α+2
#
⇒ E
¡
X2
¢
=
∂2
MX (t)
∂t2
¯
¯
¯
¯
t=0
=
α (α + 1)
θ2 =
α2
θ2 +
α
θ2 ⇒ V (X) = E(X2
) − [E(X)]2
=
α
θ2
3.2.4 Stabilité de la loi gamma par l’addition
Soient X1 et X2 deux variables aléatoires indépendantes telles que X1 Ã γ (α1, θ) et X2 Ã γ (α2, θ), alors la
variable aléatoire Y = X1 + X2 Ã γ (α1 + α2, θ) :
MY (t) = E
¡
etY
¢
= E
¡
et(X1+X2)
¢
= E
¡
etX1
¢
E
¡
etX2
¢
= MX1 (t) MX2 (t) =
·
θ
(θ − t)
¸α1
×
·
θ
(θ − t)
¸α2
=
·
θ
(θ − t)
¸α1+α2
c’est la fonction génératrice des moments d’une γ (α1 + α2, θ)
20

42. 4 La loi normale (ou loi de Laplace-Gauss) : X Ã N
¡
m, σ2
¢
4.1 Définition
On dit qu’une variable aléatoire continue X, suit une loi normale (ou de Laplace-Gauss) de paramètres (m, σ2
),
si sa densité de probabilité f est définie par :
f(x) =
1
σ
√
2Π
e
−
1
2
x − m
σ
2
∀x ∈ R
où m ∈ R et σ ∈ R∗
+ sont deux réels donnés.
On dit que X est une variable aléatoire normale et on note X Ã N
¡
m, σ2
¢
• On vérifie que
R +∞
−∞
f(x)dx = 1
En effet,
R +∞
−∞
f(x)dx =
1
σ
√
2Π
Z +∞
−∞
e
−
1
2
x − m
σ
2
dx
=
1
σ
√
2Π
Z +∞
−∞
e
−
t2
2 σdt
=
1
√
2Π
Z +∞
−∞
e
−
t2
2 dt
, posons t =
x − m
σ
⇒ x = σt + m ⇒ dx = σdt
Pour que
R +∞
−∞
f(x)dx = 1, il suffit de montrer que
Z +∞
−∞
e
−
t2
2 dt =
√
2Π.
Notons tout d’abord que cette intégrale est symétrique par rapport à 0 (e
−
t2
2 est une fonction paire) :
Z +∞
−∞
e
−
t2
2 dt = 2
Z +∞
0
e
−
t2
2 dt
posons w =
t2
2
⇒ t =
√
2w
1
2 ⇒ dt =
√
2
2
w− 1
2 dw ⇒ 2
Z +∞
0
e
−
t2
2 dt =
√
2
Z +∞
0
w− 1
2 e−w
dw =
√
2 × Γ
µ
1
2
¶
=
√
2Π
A retenir (les intégrales de Gauss) :
R +∞
−∞
e− t2
2 dt =
√
2Π et
R +∞
−∞
e−t2
dt =
√
Π
4.2 Paramètres descriptifs
4.2.1 Espérance mathématique
E(X) =
R +∞
−∞
xf(x)dx =
1
σ
√
2Π
Z +∞
−∞
xe
−
1
2
x − m
σ
2
dx , posons t =
x − m
σ
⇒ x = σt + m ⇒ dx = σdt
=
1
σ
√
2Π
Z +∞
−∞
(σt + m) e
−
t2
2 σdt
=
1
√
2Π


σ
Z +∞
−∞
te
−
t2
2 dt + m
Z +∞
−∞
e
−
t2
2 dt



=
1
√
2Π


σ


−e
−
t2
2



+∞
−∞
+ m
√
2Π


 = m
E(X) = m
21

43. 4.2.2 Variance
1`ere
méthode :
V (X) = E(X − E(X))2
= E(X − m)2
=
1
σ
√
2Π
Z +∞
−∞
(x − m)2
e
−
1
2
x − m
σ
2
dx, posons t =
x − m
σ
⇒
½
x = σt + m
dx = σdt
=
σ2
√
2Π
Z +∞
−∞
t2
e
−
t2
2 dt
en intégrant par partie : u(t) = t ⇒ u0
(t) = 1
v0
(x) = te
−
t2
2 ⇒ v(x) = −e
−
t2
2
⇒ V (X) =
σ2
√
2Π





−te
−
t2
2



+∞
−∞
+
Z +∞
−∞
e
−
t2
2 dt


 =
σ2
√
2Π
h
0 +
√
2Π
i
= σ2
V (X) = σ2
2`eme
méthode :
V (X) = E(X2
) − [E(X)]
2
avec E(X) = m
E(X2
) =
R +∞
−∞
x2
f(x)dx =
1
σ
√
2Π
Z +∞
−∞
x2
e
−
1
2
x − m
σ
2
dx , posons t =
x − m
σ
⇒
½
x = σt + m
dx = σdt
=
1
√
2Π
Z +∞
−∞
(σt + m)
2
e
−
t2
2 dt
=
1
√
2Π
Z +∞
−∞
³
(σt)2
+ 2mσt + m2
´
e
−
t2
2 dt
=
1
√
2Π


σ2
Z +∞
−∞
t2
e
−
t2
2 dt + 2mσ
Z +∞
−∞
te
−
t2
2 dt + m2
Z +∞
−∞
e
−
t2
2 dt



=
1
√
2Π


σ2





−te
−
t2
2



+∞
−∞
+
Z +∞
−∞
e
−
t2
2 dt


 + 2mσ


−e
−
t2
2



+∞
−∞
+ m2
√
2Π



=
1
√
2Π
h
σ2
√
2Π + m2
√
2Π
i
⇒ E(X2
) = σ2
+ m2
⇒ V (X) = E(X2
) − [E(X)]2
= σ2
+ m2
− m2
= σ2
4.3 Représentation graphique
f(x)
xm
1
2σ Π
m α− m α+
( ) ( )f m f mα α− = +
x m= est un axe de sym étrie
( )Mo Me E X m= = =
22

44. 4.4 Fonction de répartition
F : R −→ [0, 1]
x 7−→ F (x) = P (X < x) =
R x
−∞
f(t)dt =
1
σ
√
2Π
Z x
−∞
e
−
1
2
t − m
σ
2
dt
On vérifie que lim
x→−∞
F(x) = 0 et lim
x→+∞
F(x) =
1
σ
√
2Π
lim
x→+∞
Z x
−∞
e
−
1
2
t − m
σ
2
dt , posons z =
t − m
σ
=
1
√
2Π
lim
x→+∞
Z x−m
σ
−∞
e
−
z2
2 dz = 1
On vérifie aussi que m est la médiane :
F (m) =
1
σ
√
2Π
Z m
−∞
e
−
1
2
t − m
σ
2
dt, posons z =
t − m
σ
⇒
½
dt = σdz
lorsque t → m on a z → 0
=
1
√
2Π
Z 0
−∞
e
−
z2
2 dz =
1
√
2Π



1
2
Z +∞
−∞
e
−
z2
2 dz


 =
1
2
Graphiquement, on a l’allure suivante :
1
( )F x
xo m
0, 5
4.5 Fonction génératrice des moments
MX(t) = E(etX
) =
R +∞
−∞
etx
f(x)dx =
1
σ
√
2Π
Z +∞
−∞
etx
e
−
1
2
x − m
σ
2
dx , posons z =
x − m
σ
⇒
½
x = σz + m
dx = σdz
=
1
√
2Π
Z +∞
−∞
et(σz+m)
e− z2
2 dz
=
etm
√
2Π
Z +∞
−∞
etσz− z2
2 dz
=
etm
√
2Π
Z +∞
−∞
e− 1
2 (z2
−2tσz+(σt)2
−(σt)2
)dz
=
etm
√
2Π
Z +∞
−∞
e− 1
2 (z−tσ)2
e
(σt)2
2 dz, posons u = z − tσ ⇒ du = dz
=
etm
.e
(σt)2
2
√
2Π
Z +∞
−∞
e− u2
2 du
| {z }
√
2Π
MX(t) = etm+ σ2t2
2 ∀t ∈ R
Déduction de l’espérance et de la variance à partir de la F.G.M :
•
∂MX (t)
∂t
=
¡
m + σ2
t
¢
etm+ σ2t2
2 ⇒ E (X) =
∂MX (t)
∂t
¯
¯
¯
¯
t=0
= m
23

45. •
∂2
MX (t)
∂t2
= σ2
etm+ σ2t2
2 +
¡
m + σ2
t
¢2
etm+ σ2t2
2 ⇒ E
¡
X2
¢
=
∂2
MX (t)
∂t2
¯
¯
¯
¯
t=0
= σ2
+ m2
⇒ V (X) = E(X2
) − [E(X)]
2
= σ2
Exemple :
Si X admet la F.G.M. suivante : MX(t) = e(100t+50t2
) ∀t ∈ R, déterminer E(X) et V (X).
MX(t) = e(100t+50t2
) = e(100t+ 100
2 t2
) = e
100t+ 102
2 t2
qui est la F.G.M. d’une variable aléatoire X Ã N (100, 100)
et on a E(X) = V (X) = 100
4.6 Stabilité de la loi normale par l’addition
Soient X1 et X2 deux variables aléatoires indépendantes telles que X1 Ã N
¡
m1, σ2
1
¢
et X2 Ã N
¡
m2, σ2
2
¢
, alors
la variable aléatoire Y = X1 + X2 Ã N
¡
m1 + m2, σ2
1 + σ2
2
¢
preuve :
X1 Ã N
¡
m1, σ2
1
¢
⇒ MX1
(t) = etm1+
σ2
1t2
2
X2 Ã N
¡
m2, σ2
2
¢
⇒ MX2 (t) = etm2+
σ2
2t2
2
MY (t) = E
¡
etY
¢
= E
¡
et(X1+X2)
¢
= E
¡
etX1
¢
E
¡
etX2
¢
= MX1
(t) MX2
(t) = etm1+
σ2
1t2
2 × etm2+
σ2
2t2
2
= et(m1+m2)+
(σ2
1+σ2
2)t2
2
c’est la fonction génératrice des moments d’une N
¡
m1 + m2, σ2
1 + σ2
2
¢
. La loi normale est stable par l’addition.
4.7 La loi normale centrée réduite (ou standard) : Z Ã N (0, 1)
4.7.1 Définition
Soit Z une variable aléatoire continue. On dit que Z est une variable aléatoire normale centrée réduite si sa
densité de probabilité est définie par :
fZ(z) =
1
√
2Π
e
−
z2
2 ∀z ∈ R
et on note Z Ã N (0, 1)
4.7.2 Théorème
Si X est une variable aléatoire qui quit la loi normale de paramètres
¡
m, σ2
¢ £
X Ã N
¡
m, σ2
¢¤
, alors la variable
aléatoire Z définie par Z =
X − m
σ
suit la loi normale de paramètres (0, 1)
X Ã N
¡
m, σ2
¢
⇒ Z =
X − m
σ
à N (0, 1)
preuve :
X Ã N
¡
m, σ2
¢
⇒ MX(t) = etm+ σ2t2
2
Soit Z =
X − m
σ
⇒ MZ(t) = E(etZ
) = E(et(X−m
σ )) = E(e
−tm
σ e
tX
σ ) = e
−tm
σ E(e
tX
σ )
= e
−tm
σ MX( t
σ )
= e
−tm
σ e
tm
σ + t2
2
= e
t2
2 = e0t+ (1)2t2
2
qui est la F.G.M. d’une normale de paramètre (m = 0, σ2
= 1), donc Z =
X − m
σ
à N (0, 1)
conséquence :
La conséquence importante de ce théorème est que, par ce changement de variable, n’importe quelle loi normale
peut être ramenée à la seule loi N (0, 1)
Remarque : Si X Ã N (0, 1) alors Y = X2
à γ
µ
1
2
,
1
2
¶
On a X Ã N (0, 1) ⇒ X (Ω) = R et Y = X2
⇒ Y (Ω) = R+
24

46. ∀y ∈ R+ on a FY (y) = P(Y < y) = P(X2
< y) = P(−
√
y < X <
√
y) = FX(
√
y) − FX(−
√
y)
⇒ ∀y ∈ R∗
+ on a fY (y) = F0
Y (y) =
1
2
√
y
fX(
√
y) +
1
2
√
y
fX(−
√
y)
=
1
2
√
y
1
√
2Π
e− y
2 +
1
2
√
y
1
√
2Π
e− y
2
=
y− 1
2
√
2Π
e− y
2 =
¡1
2
¢1
2
√
Π
y
1
2 −1
e− 1
2 y
¡1
2
¢1
2
√
Π
y
1
2 −1
e− 1
2 y
est de la forme
θα
Γ (α)
yα−1
e−θy
avec θ =
1
2
; α =
1
2
et Γ
µ
1
2
¶
=
√
Π ⇒ Y = X2
à γ
µ
1
2
,
1
2
¶
.
4.7.3 Fonction de répartition de la loi normale centrée réduite
F : R −→ [0, 1]
z 7−→ FZ (z) = P (Z < z) =
R z
−∞
f(t)dt =
1
√
2Π
Z z
−∞
e
−
t2
2 dt
1
ZF
zo
0, 5
f(z)
zz
( )
ZF z
( )
2
21
2
tz
ZF z e dt−
Π−∞
= ∫
z
FZ (z) peut être lue directement dans la table 5-1
exemple : FZ (2, 07) = 0, 981 (intersection de la ligne (2) avec la colonne (0, 07))
cette table donne uniquement la valeur de FZ pour des valeurs de z positifs.
Propriétés
1. Le graphe de fZ est symétrique par rapport à l’axe des ordonnées (fZ(z) =
1
√
2Π
e
−
z2
2 est une fonction
paire : ∀z ∈ R fZ(z) = fZ(−z))
f(z)
zz-z
( )Z zF −
FZ (−z) = P(Z < −z) = P(Z > z) = 1 − P(Z < z)
= 1 − FZ (z)
FZ (−z) = 1 − FZ (z)
Exemple : FZ (−2, 07) = 1 − FZ (2, 07) = 0, 019
25

47. 2. P (|Z| < z) = P(−z < Z < z) = P(Z < z) − P(Z < −z)
= FZ (z) − FZ (−z)
= FZ (z) − [1 − FZ (z)] = 2FZ (z) − 1 (c’est aussi égal à 1 − 2FZ (−z))
f(z)
zz-z
( )P Z z<
3. P (|Z| > z) = 1 − P (|Z| < z) = 1 − [2FZ (z) − 1]
= 2 [1 − FZ (z)]
= 2FZ (−z)
f(z)
zz-z
( )P Z z>
Application :
Soit Z Ã N (0, 1)
Calculer P(Z < −1, 37) ; P (|Z| < 1, 37) et P (|Z| > 1, 37)
• P(Z < −1, 37) = P(Z > 1, 37) = 1 − P(Z < 1, 37) = 1 − FZ (1, 37) = 1 − 0, 915 = 0, 085
La variable aléatoire normale centrée réduite a 8,5% de chances de prendre une valeur inférieure à -1,37 (ou
supérieure à 1,37)
• P (|Z| < 1, 37) = 1 − 2FZ (−1, 37) = 0, 83
• P (|Z| > 1, 37) = 2FZ (−1, 37) = 0, 17
4.8 Calcul des probabilités pour une loi normale quelconque
Par le changement de variable Z =
X − m
σ
, toutes les distributions normales se ramènent à celle de la variable
normale centrée réduite Z Ã N (0, 1) pour laquelle on dispose de la table de la fonction de répartition (table 5-1).
Soit X Ã N
¡
m, σ2
¢
si a et b sont deux réels quelconques (a < b), comment calculer P (X ∈ [a, b]) ?
P (X ∈ [a, b]) = P (a < X < b) =
Z b
a
1
σ
√
2Π
e
−
(x − m)
2
2σ2
dx, posons z =
x − m
σ
⇒
½
x = σz + m
dx = σdz
=
Z b−m
σ
a−m
σ
1
√
2Π
e
−
z2
2 dz
On reconnaît sous le signe intégrale la d.d.p. d’une variable aléatoire Z Ã N (0, 1)
⇒ P (a < X < b) =
Z b−m
σ
a−m
σ
1
√
2Π
e
−
z2
2 dz = P
µ
a − m
σ
< Z <
b − m
σ
¶
avec Z =
X − m
σ
à N (0, 1)
Conclusion :
Si X Ã N
¡
m, σ2
¢
et si a et b sont deux réels quelconques (a < b), alors on a
P (a < X < b) = P
µ
a − m
σ
< Z =
X − m
σ
<
b − m
σ
¶
avec Z =
X − m
σ
à N (0, 1)
26

48. Cette relation permet de ramener tout calcul de probabilité concernant une loi N
¡
m, σ2
¢
à un calcul de proba-
bilité concernant une loi N (0, 1) pour laquelle on dispose de la table des probabilités cumulées.
Exemple :
Soit X Ã N (2, 4)
Calculer P(3 ≤ X < 4) ; P(0 ≤ X ≤ 1) ; P(0 ≤ X ≤ 3) et P(−0, 4 < X < 4, 4)
• P(3 ≤ X < 4) = P(
3 − 2
2
≤
X − 2
2
<
4 − 2
2
) = P(
1
2
≤ Z < 1)
= P(Z < 1) − P(Z <
1
2
)
= FZ (1) − FZ (0, 5)
= 0, 841 − 0, 691 = 0, 15
f(z)
z10,5
avec Z Ã N (0, 1)
• P(0 ≤ X ≤ 1) = P(
0 − 2
2
≤
X − 2
2
≤
1 − 2
2
) = P(−1 ≤ Z ≤ −
1
2
)
= P(Z ≤ −
1
2
) − P(Z < −1)
= 1 − P(Z <
1
2
) − 1 + P(Z < 1)
= P(Z < 1) − P(Z <
1
2
) = P(
1
2
< Z < 1) = 0, 15
• P(0 < X ≤ 3) = P(
0 − 2
2
<
X − 2
2
≤
3 − 2
2
) = P(−1 < Z ≤
1
2
)
= P(Z ≤
1
2
) − P(Z ≤ −1)
= P(Z ≤
1
2
) − 1 + P(Z ≤ 1)
= FZ
µ
1
2
¶
+ FZ (1) − 1 = 0, 691 + 0, 841 − 1 = 0, 532
4.9 Détermination de la valeur de la variable normale pour une aire donnée
4.9.1 Définition
Soit X une variable aléatoire continue de fonction densité fX et de fonction de répartition FX. On appelle
quantile d’ordre α de X (α ∈ ]0, 1[) , qu’on note Xα, la valeur de la variable aléatoire X telle que :
FX(Xα) = P(X < Xα) =
Z Xα
−∞
fX(x)dx = α
X
( )X
f x
Xα
( ) ( )
( )
X
X
X
F X P X X
f x dx
α
α α
α
−∞
= <
= =∫
27

49. Exemples :
1. Soit Z Ã N (0, 1), déterminer Zα telle que α = 0, 949.
FZ(Zα) = P(Z < Zα) =
R Zα
−∞
fZ(z)dz = α = 0, 949
A partir de la table 5-2 qui donne la valeur Zα pour une aire α donnée, on a
X
( )Z
f z
0,949
1, 635z =
0,949Z=
α
0, 94
0, 009
1, 635
0, 50
0
0,949α =
0
2. Soit X Ã N (5, 4), déterminer Xα telle que α = 0, 84
FX(X0,84) = P(X < X0,84) = 0, 84, posons Z =
X − m
σ
=
X − 5
2
⇒ FX(X0,84) = P(X < X0,84) = P(
X − 5
2
<
X0,84 − 5
2
) = P(Z < Z0,84 =
X0,84 − 5
2
) = 0, 84 avec
Z Ã N (0, 1)
⇒ Z0,84 =
X0,84 − 5
2
= 0, 994 ⇒ X0,84 = 2Z0,84 + 5 = 6, 988
Ainsi, le quantile d’ordre α d’une variable aléatoire X Ã N
¡
m, σ2
¢
s’obtient à partir du quantile de même
ordre α de la loi normale centrée réduite :
si X Ã N
¡
m, σ2
¢
⇒ Xα = σZα + m où Zα est le quantile d’ordre α de Z Ã N (0, 1)
4.9.2 Propriété remarquable
Si α est un niveau de probabilité et Z Ã N (0, 1), alors il existe une valeur z = Z1− α
2
, appelée quantile d’ordre
1 − α
2 de Z qui vérifie :
P(−z < Z < z) = 1 − α
En effet, P(−z < Z < z) = P(Z < z) − P(Z < −z) = P(Z < z) − [1 − P(Z < z)]
= 2P(Z < z) − 1
on a donc P(−z < Z < z) = 1 − α ⇔ 2P(Z < z) − 1 = 1 − α
⇔ 2P(Z < z) = 2 − α
⇔ P(Z < z) = 1 −
α
2
⇔ z = Z1− α
2
f(z)
z
1 α−
2
α
2
α
2
z Zα− =
1 2
z Z α=
−
21Z α= − −
La relation non centrée correspondante est :
P(m − σZ1− α
2
< X = σZ + m < m + σZ1− α
2
) = 1 − α
28

50. Exemple :
Soit Z Ã N (0, 1), déterminer z telle que P(−z < Z < z) = 0, 95.
1 − α = 0, 95 ⇒ α = 0, 05 ⇒
α
2
= 0, 025 ⇒ 1 −
α
2
= 0, 975 ⇒ z = Z1− α
2
= z0,975 = 1, 96. Ceci signifie que 95%
des valeurs de Z sont comprises entre [−1, 96; 1, 96]
Si X Ã N
¡
m, σ2
¢
⇒ 95% des valeurs de X sont comprises entre [m − 1, 96σ; m + 1, 96σ] .
4.10 La loi normale en tant que loi limite
La loi normale ou loi de Laplace-Gauss est une distribution que l’on rencontre souvent en pratique. C’est la
loi qui s’applique à une variable statistique qui est la résultante d’un grand nombre de causes indépendantes, dont
les effets s’additionnent et dont aucune n’est prépondérante. [exemple : les erreurs de mesures : omissions, faute
d’information, erreur de saisie,....].
De plus, la loi normale présente la particularité d’être une loi limite vers laquelle tendent d’autres lois.
4.10.1 Théorème centrale limite (TCL)
Si X1, X2, . . . , Xn, n variables aléatoires indépendantes et identiquement distribuées (iid) selon une même loi
quelconque d’espérance m et de variance σ2
, alors, dès que n est grand (en pratique n ≥ 30), la variable aléatoire
Y =
Pn
i=1 Xi converge vers la loi normale d’espérance mY et de variance σ2
Y avec :
mY = E(Y ) = E (
Pn
i=1 Xi) =
Pn
i=1 E(Xi) = n.m et
σ2
Y = V (Y ) = V (
Pn
i=1) =
Pn
i=1 V (Xi) = n.σ2
.
si Xi à iid(m, σ2
) i : 1 . . . n alors, si n est grand (n ≥ 30), Y =
Pn
i=1 Xi à N
¡
nm, nσ2
¢
Implication : Y =
Pn
i=1 Xi à N
¡
nm, nσ2
¢
⇒
Y − nm
√
nσ
à N (0, 1) ⇔
X − m
σ√
n
à N (0, 1)
4.10.2 Approximation d’une loi binomiale ou d’une loi de Poisson par une loi normale
a/ Approximation de la loi binomiale par la loi normale
Soit une variable aléatoire X Ã B (n, p) . Si n ≥ 30 et 0, 4 ≤ p ≤ 0, 6 alors on peut approximer cette loi B (n, p)
par une loi normale N (np, npq)
si n ≥ 30 et 0, 4 ≤ p ≤ 0, 6 alors B (n, p) ≈ N (np, npq)
b/ Approximation de la loi de Poisson par la loi normale
Soit une variable aléatoire X Ã P (λ) . Si λ ≥ 20 alors on peut approximer cette loi P (λ) par une loi normale
N (λ, λ)
si λ ≥ 20 alors P (λ) ≈ N (λ, λ)
c/ Correction de continuité
L’approximation d’une loi discrète par une loi continue pose un problème puisque cette dernière affecte une valeur
nulle à la probabilité en un point P(X = x). Pour contourner cette difficulté, on procède à une correction dite de
"continuité" de la façon suivante :
P(X = x) = P(x − 0, 5 < X < x + 0, 5)
Exemple :
Soit X une variable aléatoire qui suit la loi P (25) . On a λ = 25 > 20 ⇒ P (25) ≈ N (25, 25) .
En utilisant la loi exacte de X, on peut calculer P(X = 18) =
e−25
(25)18
18!
= 0, 031.
En utilisant la loi normale, on a P(X = 18) = P(18 − 0, 5 < X < 18 + 0, 5) avec X
≈
à N (25, 25)
= P(
18 − 0, 5 − 25
5
<
X − 25
5
<
18 + 0, 5 − 25
5
)
= P(−1, 5 < Z < −1, 3) avec Z Ã N (0, 1)
= P(1, 3 < Z < 1, 5)
= FZ(1, 5) − FZ(1, 3)
= 0, 933 − 0, 903 = 0, 030
29

51. Troisième partie
Les lois dérivées de la loi normale
Contrairement à toutes les lois continues que nous venons de présenter et qui sont définies directement par leurs
densités de probabilité, les lois de khi-deux, de Student et de Fisher sont définies par des transformations sur des
variables aléatoires normales.
1 La loi de khi-deux : X Ã χ2
(n)
1.1 Définition
Soient X1, X2, . . . , Xn; n V.A. indépendantes qui suivent la loi normale centrée réduite (Xi à N (0, 1) ∀i :
1 . . . n). On appelle loi de khi-deux à n degrés de liberté, la loi suivie par X =
Pn
i=1 X2
i et on note X Ã χ2
(n).
1.2 Densité de probabilité
Si X Ã χ2
(n) alors la densité de probabilité de X est donnée par :
f(x) =
⎧
⎪⎨
⎪⎩
1
2(n/2)Γ
³n
2
´x(n/2)−1
e−x/2
si x > 0
0 si x ≤ 0
avec Γ (α) =
R +∞
0
tα−1
e−t
dt.
Remarque :
Si X Ã N (0, 1) alors X2
à χ2
(1) ≡ γ
µ
1
2
,
1
2
¶
.
1.3 Paramètres descriptifs
Rappelons que si X Ã γ (α, θ) alors :
f(x) =
⎧
⎨
⎩
θα
Γ (α)
xα−1
e−θx
si x > 0
0 sinon
; E(X) =
α
θ
; V (X) =
α
θ2 et MX (t) =
∙
θ
(θ − t)
¸α
Si X Ã χ2
(n) ⇒ f(x) =
1
2(n/2)Γ
³n
2
´x(n/2)−1
e−x/2
si x > 0
=
µ
1
2
¶n/2
Γ
³n
2
´ x(n/2)−1
e−x/2
qui est la d.d.p d’une γ
µ
n
2
,
1
2
¶
On peut donc déduire que :
E
£
χ2
(n)
¤
= E
∙
γ
µ
n
2
,
1
2
¶¸
=
n/2
1/2
= n et V
£
χ2
(n)
¤
= V
∙
γ
µ
n
2
,
1
2
¶¸
=
n/2
1/4
= 2n
On retient que si :
X Ã χ2
(n) ⇒ E(X) = n et V (X) = 2n = 2E(X)
Remarque :
La Fonction génératrice des moments d’une χ2
(n) est celle d’une γ
µ
n
2
,
1
2
¶
:
MX (t) =
∙
1/2
1/2 − t
¸n/2
=
∙
1
1 − 2t
¸n/2
30

52. 1.4 Lecture de la table de la loi de khi-deux
La loi de khi-deux n’est pas symétrique, la courbe de la densité de probabilité d’une variable aléatoire X qui
suit une loi de khi-deux est asymétrique étalée à droite.
2
αχ
2
( )P X αχ α< = 2
( ) 1P X αχ α> = −
x
f(x)
La table de la loi de khi-deux donne pour différentes valeurs de degrés de liberté (n), la valeur de χ2
α telle que
P(X < χ2
α) = α.
Exemple : Si X Ã χ2
(4). Déterminer χ2
α telle que α = 0, 8.
/n α
1
0, 005
2
3
4
0, 80
30
0, 995
5, 989
2
αχ
⎫⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎬
⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎪
}
2
( )P X α
χ α< =
degrés de liberté: n
D’après la table de la loi de khi-deux, on a χ2
0,8 = 5, 989 ⇒ 80% des valeurs de X sont inférieures à 5, 989.
1.5 Approximation de la loi de khi-deux par la loi normale
Soit X une variable aléatoire qui suit la loi de khi-deux à n degrés de liberté (X Ã χ2
(n)). Lorsque n ≥ 30, on
admettra que la quantité
√
2X −
√
2n − 1 Ã N(0, 1).
Exemple : Déterminer le quantile d’ordre α = 0, 975 d’une khi-deux à 60 degrés de liberté.
On a X Ã χ2
(60) ⇒ Z =
√
2X −
p
2 (60) − 1 Ã N(0, 1)
⇒ 0, 975 = P (Z < Z0,975) = P
³√
2X −
√
119 < Z0,975
´
= P
µ
X <
[Z0,975+
√
119]2
2
¶
⇒ χ2
0,975(60) =
£
Z0,975 +
√
119
¤2
2
=
£
1, 96 +
√
119
¤2
2
' 83 (la valeur exacte de χ2
0,975(60) = 83, 298. Table 6)
1.6 Stabilité de la loi de khi-deux
Si X1 et X2 sont deux variables aléatoires indépendantes telles que X1 Ã χ2
(n1) et X2 Ã χ2
(n2), alors la
variable aléatoire Y définie par Y = X1 + X2 Ã χ2
(n1 + n2).
MY (t) = E
¡
etY
¢
= E
¡
et(X1+X2)
¢
= E
¡
etX1
¢
E
¡
etX2
¢
= MX1 (t) MX2 (t) =
∙
1
1 − 2t
¸n1/2
×
∙
1
1 − 2t
¸n2/2
=
∙
1
1 − 2t
¸n1+n2/2
31

53. c’est la fonction génératrice des moments d’une χ2
(n1 + n2).
Remarque1 :
χ2
(n − 1) + χ2
(1) = χ2
(n) ⇒ χ2
(n − 1) = χ2
(n) − χ2
(1)
Remarque2 :
Si X Ã χ2
(n) ⇒ pour λ 6= 1, Y = λX 6Ã χ2
(λn)
On sait que pour une khi-deux, on a toujours : V (χ2
) = 2E(χ2
)
Pour Y = λX on a :
E(Y ) = λE(X) = λn
V (Y ) = λ2
V (X) = λ2
2n
¾
⇒ V (Y ) 6= 2E(Y ) ⇒ Y ne suit pas une χ2
(λn).
1.7 Application
Soient X1, X2, . . . , Xn, n variables aléatoires indépendantes et identiquement distribuées (iid) selon une même
loi quelconque d’espérance m et de variance σ2
. Déterminer la loi de probabilité de n
µ
X − m
σ
¶2
lorsque n > 30.
D’après le TCL, on a
Pn
i=1 Xi à N
¡
nm, nσ2
¢
⇒
Pn
i=1 Xi − nm
√
nσ
à N (0, 1)
⇒
nX − nm
√
nσ
à N (0, 1)
⇒
X − m
σ/
√
n
à N (0, 1) ⇒
µ
√
n
X − m
σ
¶2
= n
µ
X − m
σ
¶2
à χ2
(1)
2 La loi de Student : T Ã T (n)
2.1 Définition
Soient X et Y deux variables aléatoires indépendantes qui suivent respectivement la loi normale centrée réduite
et la loi de khi-deux à n degrés de liberté. Considérons la variable aléatoire T =
X
q
Y
n
, la loi de probabilité de T est
appelée loi de Student à n degrés de liberté. On note T Ã T (n) .
N (0, 1)
r
χ2
(n)
n
à T (n)
2.2 Densité de probabilité
Si T Ã T (n) alors la densité de probabilité de T est donnée par :
f (t) =
1
√
nβ
¡1
2 , n
2
¢
µ
1 +
t2
n
¶−(n+1
2 )
∀t ∈ R
où β (a, b) =
Γ (a) .Γ (b)
Γ (a + b)
a > 0; b > 0.
⇒ β
¡1
2 , n
2
¢
=
Γ
¡1
2
¢
.Γ
¡n
2
¢
Γ
¡n+1
2
¢ =
√
Π.Γ
¡n
2
¢
Γ
¡n+1
2
¢
⇒
f (t) =
Γ
¡n+1
2
¢
√
nΠ × Γ
¡n
2
¢
µ
1 +
t2
n
¶(n+1
2 )
∀t ∈ R
Remarques :
• ∀t ∈ R, on a f (−t) = f (t) ⇒ la loi de Student est symétrique par rapport à (x = 0) .
• Plus le nombre de degrés de liberté est faible, plus la courbe de la d.d.p de la loi de Student est aplatie, signe
de dispersion plus grande.
32

54. • Si α est un niveau de probabilité et T Ã T (n), alors il existe une valeur t = T
(n)
1− α
2
, appelée quantile d’ordre
1 − α
2 de T qui vérifie :
P(−t < T < t) = P(|T| < t) = 1 − α
f(t)
T
1 α− 2
α
2
α
( )
2
n
t Tα− =
( )
1 2
n
t T α=
−
( )
1 2
n
T α= −
−
Student à n degrès de liberté
Student à n' degrès de liberté ( )'n n<
2.3 Lecture de la table de la loi de Student
La table de la loi de Student donne pour différentes valeurs de degrés de liberté (n), la valeur de T
(n)
α telle que
P(T < T
(n)
α ) = α.
Exemple1 : Si T Ã T (4) . Déterminer T
(4)
α telle que α = 0, 8.
/n α
1
0, 55
2
3
4
0, 80
30
0, 995
0, 941 Tα
⎫⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎬
⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎪
}
degrés de liberté: n
( )P T Tα α< =
D’après la table de la loi de Student, on a T
(4)
0,8 = 0, 941 ⇒ 80% des valeurs de T sont inférieures à 0, 941.
Exemple2 : Si T Ã T (4) . Déterminer la valeur de t telle que P(|T| > t) = 0, 4.
P(|T| > t) = 0, 4 ⇒ P(T > t) = P(T < −t) = 0, 2 (la loi de Student est symétrique par rapport à 0)
⇒ P(T < t) = 0, 8
⇒ t = T
(4)
0,8 = 0, 941
f(t)
T
0, 60, 2
( )
0,2
4
t T− =
( )
0,8
4
t T=
( )
0,8
4
T= −
0, 2
33

55. 2.4 Approximation de la loi de Student par la loi normale
Si n ≥ 30, la loi de Student peut être approximée par la loi normale centrée réduite :
si n ≥ 30 ⇒ T (n) ≈ N(0, 1)
3 La loi de Fisher : F Ã F (n, m)
3.1 Définition
Soient X et Y deux variables aléatoires indépendantes qui suivent respectivement les lois de χ2
(n) et χ2
(m).
Considérons la variable aléatoire F =
X/n
Y/m
, la loi de probabilité de F est appelée loi de Fisher-Snedecor à n et m
degrés de liberté. On note F Ã F (n, m) .
χ2
(n)/n
χ2
(m)/m
à F (n, m)
3.2 Densité de probabilité
On dit que la variable aléatoire F suit la loi de Fisher à (n, m) degrés de liberté si elle admet pour densité de
probabilité :
g (f) =
⎧
⎪⎨
⎪⎩
nn/2
.mm/2
β
¡n
2 , m
2
¢
f(n/2)−1
(m + nf)(n+m
2 )
si f > 0; (m, n ∈ N∗
)
0 sinon
où β
¡n
2 , m
2
¢
=
Γ
¡n
2
¢
.Γ
¡m
2
¢
Γ
¡n+m
2
¢
Remarque :
Si T Ã T (n), alors T2
à F (1, n)
On a par définition : T Ã T (n) ⇒ T =
X
q
Y
n
avec X Ã N (0, 1) et Y Ã χ2
(n)
⇒ T2
=
X2
Y/n
avec X2
à χ2
(1). T2
est donc le rapport de deux khi-deux divisées par leurs degrés de liberté :
T2
=
X2
Y/n
=
χ2
(1)/1
χ2(n)/n
à F (1, n) .
3.3 Lecture de la table
• La courbe de la loi de Fisher est asymétrique étalée à droite.
• La table de la loi de Fisher donne, pour diverses valeurs de n et m et pour une probabilité α donnée, les
valeurs de F
(n,m)
α telle que P(F > F
(n,m)
α ) = α. (ici F
(n,m)
α n’est pas le quantile d’ordre α, elle indique plutôt la
valeur de F qui a une probabilité α d’être dépassée)
( )P F Fα α> =
F
g(f)
Fα
1 α−
34

56. Exemple1 : Si F Ã F (15, 10) . Déterminer F
(15,10)
α telle que α = 0, 01.
0, 01α =
1
11
10
15 20
4, 558
( ),n m
Fα
⎫⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎬
⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎪
( ),( )n mP F Fα =>
Degrés de liberté du num érateur: n
ddldudénominateur:m
D’après la table 8-2 de la loi de Fisher, on a F
(15,10)
0,01 = 4, 558 ⇒ 1% des valeurs de F (F Ã F (15, 10)) sont
supérieures à 4, 558.
Exemple2 : Si F Ã F (15, 10) . Déterminer F
(15,10)
0,99 .
Dans ce cas, on utilise la propriété suivante :
si F Ã F (n, m) alors
1
F
à F (m, n) et F
(m,n)
1−α =
1
F
(n,m)
α
En effet, si F Ã F (n, m) ceci implique que F =
X/n
Y/m
avec X Ã χ2
(n) et Y Ã χ2
(m), d’où
1
F
=
Y/m
X/n
à F (m, n) .
Pour α donnée, on peut donc écrire : α = P
³
F(n,m)
> F
(n,m)
α
´
= P
µ
1
F(n,m)
<
1
F
(n,m)
α
¶
= 1 − P
µ
F(m,n)
>
1
F
(n,m)
α
¶
⇒ P
µ
F(m,n)
>
1
F
(n,m)
α
¶
= 1 − α ⇒ F
(m,n)
1−α =
1
F
(n,m)
α
On a donc, F
(15,10)
0,99 =
1
F
(10,15)
0,01
=
1
3, 805
= 0, 263.
D’après ce qui précède, on peut conclure que, si F Ã F (15, 10), alors 98% des valeurs de F sont comprises entre
0, 263 et 4, 558.
35

57. K&M http ://stat.fateback.com
Chapitre 3
Echantillonnage et Estimation
1 Introduction
La statistique inférentielle (inductive ou encore la statistique mathématique) repose sur l’idée suivante :
Etant donné un ensemble d’individus P (encore appelé population ou univers) dont les caractéristiques ne
sont pas connues. A partir de l’observation d’un sous-ensemble d’individus de cette population, l’échantillon, on
va chercher à déterminer, à induire les principales caractéristiques de la population (sa moyenne, sa variance, sa
distribution...).
La statistique mathématique ou inférence statistique élabore des méthodes qui, au vu des résultats d’un échan-
tillon, permettent de porter un jugement et de prendre des décisions à l’échelle de la population entière. Il s’agit
d’une démarche qui va du particulier, l’échantillon, au général, la population.
Essayer par des jugements sur échantillon, d’induire les caractéristiques d’une population entière nécessite au
départ la construction d’une théorie de l’échantillonnage et l’établissement des propriétés d’un échantillon. Cet
ensemble de fondements théoriques va permettre ensuite l’élaboration de méthodes et principes particuliers tels que
l’estimation ponctuelle, l’estimation ensembliste ou par intervalle de confiance, et les tests statistiques.
2 L’échantillonnage
Plusieurs méthodes peuvent être utilisées pour sélectionner un échantillon dans une population, l’une des plus
courantes est l’échantillonnage aléatoire simple qui correspond à des tirages équiprobables et indépendants les uns
des autres.
2.1 L’échantillon aléatoire simple
Un échantillon aléatoire simple (EAS) de taille n, issu d’une population X de loi de probabilité L, est une suite
(X1, X2, . . . , Xn) de variables aléatoires où les Xi, (i : 1 . . . n) sont deux à deux indépendantes et ont la même loi
de probabilité L que X. On dit que l’échantillon est iid de X (abréviation signifiant que les variables aléatoires Xi
sont indépendantes et identiquement distribuées selon la loi de X)
2.2 Paramètres et Statistiques
On distingue au niveau du vocabulaire, les mesures faites dans une population de celles faites dans un échantillon.
Les mesures qui servent à décrire une population portent le nom de paramètres, alors que celles qui servent à
décrire un échantillon portent le nom de statistiques.
Exemple : La moyenne m de la population est un paramètre. La moyenne X de l’échantillon est une statistique.
2.2.1 Définition d’une statistique
Soit (X1, X2, . . . , Xn) un échantillon EAS iid de taille n, issu d’une population X de moyenne m et de variance
σ2
. On appelle statistique (T) toute variable aléatoire qui est fonction de l’échantillon : T = f (X1, X2, . . . , Xn) .
Les caractéristiques de position (mode, médiane, moyenne. . . ) ou de dispersion (écart absolu moyen, variance,
écart-type. . . ) sont des exemples de statistiques T.
Dans ce qui suit, trois d’entre elles sont plus spécialement utilisées :
X : la moyenne de l’échantillon.
S02
et S2
: la variance empirique et la variance empirique corrigée.
2.3 Caractéristiques d’un échantillon aléatoire
Soit (X1, X2, . . . , Xn) un EAS iid de taille n, issu d’une population X de moyenne m et de variance σ2
, on
appelle :
— Moyenne empirique (ou échantillonnale), la variable aléatoire X définie par : X =
1
n
Pn
i=1 Xi.
35

58. — Variance empirique, la variable aléatoire S02
définie par : S02
=
1
n
Pn
i=1
¡
Xi − X
¢2
.
— Variance empirique corrigée, la variable aléatoire S2
définie par : S2
=
1
n − 1
Pn
i=1
¡
Xi − X
¢2
.
2.3.1 Caractéristiques de la moyenne d’un échantillon
a/ Espérance de X
E(X) = E
µ
1
n
Pn
i=1 Xi
¶
=
1
n
Pn
i=1 E (Xi)
| {z }
m
=
1
n
.n.m = m
b/ Variance de X
V (X) = V
µ
1
n
Pn
i=1 Xi
¶
=
1
n2
Pn
i=1 V (Xi)
| {z }
σ2
=
1
n2
.n.σ2
=
σ2
n
2.3.2 Caractéristiques de la variance d’un échantillon
a/ Espérance de S02
et S2
• E(S02
) = E
µ
1
n
Pn
i=1
¡
Xi − X
¢2
¶
= E
µ
1
n
Pn
i=1
¡
(Xi − m) −
¡
X − m
¢¢2
¶
= E
µ
1
n
Pn
i=1
³
(Xi − m)
2
− 2 (Xi − m)
¡
X − m
¢
+
¡
X − m
¢2
´¶
= E
µ
1
n
³Pn
i=1 (Xi − m)2
− 2
¡
X − m
¢ Pn
i=1 (Xi − m) +
Pn
i=1
¡
X − m
¢2
´¶
= E
µ
1
n
³Pn
i=1 (Xi − m)
2
− 2
¡
X − m
¢
(
Pn
i=1 Xi − nm) + n
¡
X − m
¢2
´¶
= E
µ
1
n
Pn
i=1 (Xi − m)2
− 2
¡
X − m
¢2
+
¡
X − m
¢2
¶
= E
µ
1
n
Pn
i=1 (Xi − m)2
¶
− E
¡
X − m
¢2
or m = E(Xi) = E(X)
=
1
n
Pn
i=1 E (Xi − E(Xi))2
− E
¡
X − E(X)
¢2
=
1
n
Pn
i=1 V (Xi) − V
¡
X
¢
= σ2
−
σ2
n
=
σ2
(n − 1)
n
• E(S2
) = E
µ
1
n − 1
Pn
i=1
¡
Xi − X
¢2
¶
=
n
n − 1
E
µ
1
n
Pn
i=1
¡
Xi − X
¢2
¶
=
n
n − 1
E
³
S
0
2
´
=
n
n − 1
σ2
(n − 1)
n
= σ2
b/ Variance de S02
et S2
On démontre dans le cas d’un échantillon aléatoire simple issu d’une population normale que :
V (S02
) =
2 (n − 1)
n2
σ4
V (S2
) =
2σ4
n − 1
36

59. 3 Distributions d’échantillonnage
3.1 Loi (ou distribution d’échantillonnage) de X
Théorème 1 Soit (X1, X2, . . . , Xn) un EAS iid de taille n, issu d’une population X normale, de moyenne m et
de variance σ2
, alors la moyenne empirique X est normalement distribuée de moyenne m et de variance
σ2
n
.
Preuve. On sait que la loi normale est stable par l’addition :
Si on a n variables aléatoires indépendantes X1, X2, . . . , Xn avec Xi à N(m, σ2
) ∀i : 1 . . . n,
alors
nP
i=1
Xi à N(E (
Pn
i=1 Xi) , V (
Pn
i=1 Xi)) = N(nm, nσ2
)
La loi normale est également stable par transformation linéaire :
Si X Ã N(m, σ2
) ⇒ Y = aX + b à N (E (Y ) , V (Y ))
à N
¡
aE(X) + b, a2
V (X)
¢
à N
¡
am + b, a2
σ2
¢
Or X =
1
n
Pn
i=1 Xi avec Xi à N(m, σ2
) ∀i : 1 . . . n
Ainsi X Ã N(E
¡
X
¢
, V
¡
X
¢
) = N(m,
σ2
n
)
Conséquence : X Ã N(m,
σ2
n
) ⇒
X − m
σ
√
n
à N(0, 1).
Théorème 2 Soit (X1, X2, . . . , Xn) un EAS iid de taille n assez élevée (en pratique n ≥ 30), issu d’une population
X quelconque, de moyenne m et de variance σ2
, alors la moyenne empirique X est normalement distribuée de
moyenne m et de variance
σ2
n
.
Preuve. X Ã Lqcq(m, σ2
)
(X1, X2, . . . , Xn) iid de X ⇒
½
Les Xi sont indépendantes
Xi à Lqcq(m, σ2
) ∀i : 1 . . . n
n ≥ 30
TCL
=⇒
nP
i=1
Xi à N(E (
Pn
i=1 Xi) , V (
Pn
i=1 Xi)) = N(nm, nσ2
) ⇒ X Ã N(m,
σ2
n
)
3.2 Lois de la variance empirique et de la variance empirique corrigée
Théorème 3 Soit (X1, X2, . . . , Xn) un EAS iid de taille n, issu d’une population X normale, de moyenne m et
de variance σ2
, alors :
1. La statistique
nS02
σ2
à χ2
(n − 1) .
2. La statistique
(n − 1) S2
σ2
à χ2
(n − 1) .
Preuve.
1.
nS02
σ2
=
n
σ2
1
n
Pn
i=1
¡
Xi − X
¢2
=
1
σ2
Pn
i=1
¡
Xi − X
¢2
=
1
σ2
hPn
i=1 (Xi − m)
2
− n
¡
X − m
¢2
i
=
Pn
i=1
µ
Xi − m
σ
¶2
− n
µ
X − m
σ
¶2
Or on sait que : Xi à N(m, σ2
) ⇒
Xi − m
σ
à N(0, 1)
⇒
Pn
i=1
µ
Xi − m
σ
¶2
à χ2
(n)
37

60. et X Ã N(m,
σ2
n
) ⇒
X − m
σ/
√
n
à N(0, 1)
⇒
µ
X − m
σ/
√
n
¶2
= n
µ
X − m
σ
¶2
à χ2
(1)
et on a donc
nS02
σ2
à χ2
(n − 1) = χ2
(n) − χ2
(1)
Remarque :
En posant S02
0 =
1
n
Pn
i=1 (Xi − m)2
on a
nS02
0
σ2
=
n
σ2
1
n
Pn
i=1 (Xi − m)2
=
Pn
i=1
µ
Xi − m
σ
¶2
à χ2
(n)
2. De la même manière, on démontre que
(n − 1) S2
σ2
à χ2
(n − 1)
Remarque :
•
nS02
σ2
à χ2
(n − 1) ⇒ V
µ
nS02
σ2
¶
= V
¡
χ2
(n − 1)
¢
= 2 (n − 1)
⇒
n2
σ4
V
¡
S02
¢
= 2 (n − 1) ⇒ V
¡
S02
¢
=
2 (n − 1)
n2
σ4
•
(n − 1) S2
σ2
à χ2
(n − 1) ⇒ V (S2
) =
2σ4
n − 1
Théorème 4 Soit (X11, X12, . . . , X1n1 ) un EAS iid de taille n1, issu d’une population X1 normale, de moyenne m1
et de variance σ2
1 et soit (X21, X22, . . . , X2n2 ) un deuxième EAS iid de taille n2, issu d’une population X2 normale,
de moyenne m2 et de variance σ2
2, alors la variable aléatoire :
Q =
(n1 − 1) S2
1
σ2
1
Á
(n1 − 1)
(n2 − 1) S2
2
σ2
2
Á
(n2 − 1)
=
S2
1
±
σ2
1
S2
2/ σ2
2
à F (n1 − 1, n2 − 1)
Preuve. D’après le théorème 3, on a :
(n1 − 1) S2
1
σ2
1
à χ2
(n1 − 1) et
(n2 − 1) S2
2
σ2
2
à χ2
(n2 − 1)
⇒ Q =
(n1 − 1) S2
1
σ2
1
Á
(n1 − 1)
(n2 − 1) S2
2
σ2
2
Á
(n2 − 1)
=
χ2
(n1 − 1)
±
(n1 − 1)
χ2 (n2 − 1)/ (n2 − 1)
à F (n1 − 1, n2 − 1)
Remarque : si σ2
1 = σ2
2 alors Q =
S2
1
S2
2
à F (n1 − 1, n2 − 1) .
3.3 Loi de
X − m
S/
√
n
Théorème 5 Soit (X1, X2, . . . , Xn) un EAS iid de taille n, issu d’une population X normale, de moyenne m et
de variance σ2
, alors la variable aléatoire
X − m
S/
√
n
à T (n − 1) .
Preuve. D’après le théorème 1, on a :
X Ã N(m,
σ2
n
) ⇒
X − m
σ/
√
n
à N(0, 1).
D’après le théorème 3, on a :
(n − 1) S2
σ2
à χ2
(n − 1) .
D’après la définition de la loi de Student, on a :
X − m
σ/
√
n
v
u
u
t
(n − 1) S2
σ2
(n − 1)
=
X − m
σ
√
n
×
σ
S
=
X − m
S
√
n
à T (n − 1)
38

61. 3.4 Loi de X1 − X2
Théorème 6 Soit (X11, X12, . . . , X1n1 ) un EAS iid de taille n1, issu d’une population X1 normale, de moyenne m1
et de variance σ2
1 et soit (X21, X22, . . . , X2n2 ) un deuxième EAS iid de taille n2, issu d’une population X2 normale,
de moyenne m2 et de variance σ2
2, alors la variable aléatoire :
¡
X1 − X2
¢
− (m1 − m2)
s
σ2
1
n1
+
σ2
2
n2
à N(0, 1)
Preuve. D’après le théorème 1, on a :
X1 Ã N(m1,
σ2
1
n1
) et X2 Ã N(m2,
σ2
2
n2
)
⇒ X1 − X2 Ã N
¡
E
¡
X1 − X2
¢
, V
¡
X1 − X2
¢¢
⇒ X1 − X2 Ã N
µ
m1 − m2,
σ2
1
n1
+
σ2
2
n2
¶
⇒
¡
X1 − X2
¢
− (m1 − m2)
s
σ2
1
n1
+
σ2
2
n2
à N(0, 1)
Remarque1 : Dans le cas où les deux populations X1 et X2 sont quelconques et la taille des échantillons est
assez élevée (n1 ≥ 30 et n2 ≥ 30), on a également :
¡
X1 − X2
¢
− (m1 − m2)
s
σ2
1
n1
+
σ2
2
n2
à N(0, 1)
Preuve. On utilise le théorème 2 : c.-à-d. on utilise le théorème central limite pour montrer que X1 Ã N(m1,
σ2
1
n1
)
et X2 Ã N(m2,
σ2
2
n2
)
Remarque2 : Dans le cas où les deux populations X1 et X2 sont normales de variances σ2
1 et σ2
2 inconnues mais
égales
¡
σ2
1 = σ2
2 = σ2
¢
, on a :
¡
X1 − X2
¢
− (m1 − m2)
sµ
1
n1
+
1
n2
¶ µ
(n1 − 1) S2
1 + (n2 − 1) S2
2
n1 + n2 − 2
¶ Ã T (n1 + n2 − 2)
Preuve. On a d’une part : X1 Ã N(m1,
σ2
n1
) et X2 Ã N(m2,
σ2
n2
)
⇒ X1 − X2 Ã N
µ
m1 − m2, σ2
µ
1
n1
+
1
n2
¶¶
⇒
¡
X1 − X2
¢
− (m1 − m2)
σ
r
1
n1
+
1
n2
à N(0, 1)
D’autre part :
(n1 − 1) S2
1
σ2
à χ2
(n1 − 1) et
(n2 − 1) S2
2
σ2
à χ2
(n2 − 1)
⇒
(n1 − 1) S2
1 + (n2 − 1) S2
2
σ2
à χ2
(n1 + n2 − 2)
D’après la définition de la loi de Student, on a :¡
X1 − X2
¢
− (m1 − m2)
σ
r
1
n1
+
1
n2
v
u
u
t
(n1 − 1) S2
1 + (n2 − 1) S2
2
σ2
n1 + n2 − 2
à T (n1 + n2 − 2)
39

62. ⇔
¡
X1 − X2
¢
− (m1 − m2)
σ
r
1
n1
+
1
n2
×
1
1
σ
s
(n1 − 1) S2
1 + (n2 − 1) S2
2
n1 + n2 − 2
à T (n1 + n2 − 2)
⇔
¡
X1 − X2
¢
− (m1 − m2)
sµ
1
n1
+
1
n2
¶ µ
(n1 − 1) S2
1 + (n2 − 1) S2
2
n1 + n2 − 2
¶ Ã T (n1 + n2 − 2)
3.5 Distribution d’échantillonnage d’une fréquence
On suppose que dans la population mère, la proportion des individus qui possèdent un caractère X distribué
selon la loi de Bernoulli de paramètre p (X Ã B (1, p)) . Si on tire de cette population un EAS (X1, X2, . . . , Xn)
iid de taille n, alors la fréquence de ceux qui possèdent le caractère X dans l’échantillon est :
F =
1
n
nX
i=1
Xi
3.5.1 Espérance et variance de F
a/ Espérance
On a X Ã B (1, p)
et (X1, X2, . . . , Xn) iid de X ⇒
½
Les Xi sont indépendantes
Xi à B (1, p) ∀i : 1 . . . n ⇒ E(Xi) = p et V (Xi) = pq
Ainsi E (F) = E
µ
1
n
Pn
i=1 Xi
¶
=
1
n
E (
Pn
i=1 Xi) =
1
n
Pn
i=1 E (Xi) = p
L’espérance de la proportion échantillonnale F est égale à la vraie proportion p de la population.
b/ Variance
V (F) = V
µ
1
n
Pn
i=1 Xi
¶
=
1
n2
V (
Pn
i=1 Xi) =
1
n2
Pn
i=1 V (Xi) =
pq
n
3.5.2 Loi de probabilité de F
Théorème 7 Soit (X1, X2, . . . , Xn) un EAS iid de taille n assez élevée (n ≥ 30), issu d’une population X qui suit
la loi de Bernoulli de paramètre p, alors :
F =
1
n
Pn
i=1 Xi à N
µ
p,
p (1 − p)
n
¶
⇒
F − p
r
p (1 − p)
n
à N (0, 1)
Ce théorème est une conséquence du théorème central limite
3.5.3 Distribution de la différence des fréquences
Théorème 8 Soient (X11, X12, . . . , X1n1 ) et (X21, X22, . . . , X2n2 ) deux EAS iid de taille respectivement n1 et n2
assez élevées (n1 ≥ 30 et n2 ≥ 30), issus de deux populations X1 et X2 Bernoulliennes indépendantes, de paramètres
respectivement p1 et p2, alors la variable aléatoire :
F1 − F2 Ã N
µ
p1 − p2,
p1 (1 − p1)
n1
+
p2 (1 − p2)
n2
¶
⇒
(F1 − F2) − (p1 − p2)
r
p1q1
n1
+
p2q2
n2
à N (0, 1)
40

63. 4 L’estimation ponctuelle
4.1 Estimation et estimateur
Soit (X1, X2, . . . , Xn) un EAS iid de taille n, issu d’une population X de loi de probabilité L de paramètre θ
inconnu.
• On appelle estimateur ponctuel de θ, et on le note ˆΘ, toute statistique ˆΘ = f (X1, X2, . . . , Xn) utilisée pour
évaluer le paramètre inconnu θ.
• On appelle estimation, qu’on note par ˆθ = f (x1, x2, . . . , xn) , une réalisation de la statistique ˆΘ = f (X1, X2, . . . , Xn)
(toute valeur ˆθ prise par ˆΘ est une estimation de θ).
Un estimateur étant une variable aléatoire (puisque fonction d’un échantillon aléatoire), il est donc naturel
de s’intéresser, d’une part, à sa distribution de probabilité (en particulier à ses moments), d’autre part, à son
comportement asymptotique (lorsque la taille n des échantillons sur lesquels on travaille augmente).
4.1.1 Biais d’un estimateur
Définition 1 : On appelle biais (déformation) d’un estimateur ˆΘ de θ le réel B
³
ˆΘ
´
défini par :
B
³
ˆΘ
´
= E
³
ˆΘ
´
− θ
Définition 2 : Un estimateur ˆΘ de θ est dit sans biais (ou encore non biaisé ou centré), si quelque soit la vraie
valeur de du paramètre inconnu θ et quelque soit la taille n de l’échantillon, on a :
E
³
ˆΘ
´
= θ c.-à-d. B
³
ˆΘ
´
= 0
L’absence de biais est une propriété souhaitée d’un estimateur, elle signifie que les réalisations de ˆΘ sont distri-
buées autour de la vraie valeur de θ.
Définition 3 : Un estimateur ˆΘ de θ est dit asymptotiquement sans biais si :
lim
n→+∞
E
³
ˆΘ
´
= θ ⇔ lim
n→+∞
B
³
ˆΘ
´
= 0
Exemples :
Soit (X1, X2, . . . , Xn) un EAS iid de taille n, issu d’une population X de moyenne m et de variance σ2
inconnues.
On a vu, lors de l’étude des caractéristiques d’un échantillon aléatoire, que :
E(X) = m; E
¡
S2
¢
= σ2
et E(S02
) =
σ2
(n − 1)
n
Ainsi on peut dire que :
1. La moyenne empirique X est un estimateur sans biais de la moyenne théorique m :
E(X) = m ⇒ B(X) = E(X) − m = m − m = 0
2. La variance empirique corrigée S2
est un estimateur sans biais de σ2
:
E
¡
S2
¢
= σ2
⇒ B(S2
) = E
¡
S2
¢
− σ2
= 0
3. La variance empirique S
0
2
est un estimateur biaisé de σ2
mais asymptotiquement sans biais :
E(S02
) =
σ2
(n − 1)
n
⇒ B(S02
) =
σ2
(n − 1)
n
− σ2
=
−σ2
n
lim
n→+∞
E(S02
) = σ2
⇔ lim
n→+∞
B(S02
) = 0
41

64. 4.1.2 Convergence d’un estimateur
Définition : Un estimateur ˆΘ de θ est dit convergent, s’il converge en probabilité vers θ (ˆΘ
P
−→ θ), c.-à-d :
∀ε > 0 lim
n→+∞
P
³¯
¯
¯ˆΘ − θ
¯
¯
¯ > ε
´
= 0
lim
n→+∞
P
³¯
¯
¯ˆΘ − θ
¯
¯
¯ ≤ ε
´
= 1
N.B : Une condition suffisante pour que ˆΘ converge en probabilité vers θ est que :
lim
n→+∞
E
³
ˆΘ
´
= θ et lim
n→+∞
V
³
ˆΘ
´
= 0
Exemple :
Soit (X1, X2, . . . , Xn) un EAS iid de taille n, issu d’une population X de moyenne m et de variance σ2
inconnues :
1. La moyenne empirique X est un estimateur convergent de m :
E(X) = m et lim
n→+∞
V
¡
X
¢
= lim
n→+∞
σ2
n
= 0
2. Lorsque la population est normale : la variance empirique S
0
2
et la variance empirique corrigée S2
sont deux
estimateurs convergents de σ2
:
a/ E(S02
) =
σ2
(n − 1)
n
et V (S02
) =
2 (n − 1) σ4
n2
⇒ lim
n→+∞
E(S02
) = σ2
et lim
n→+∞
V
¡
S02
¢
= 0.
b/ E
¡
S2
¢
= σ2
et V
¡
S2
¢
=
2σ4
n − 1
⇒ lim
n→+∞
V
¡
S2
¢
= 0.
L’intérêt de disposer d’un estimateur ˆΘ convergent est que, dès lors qu’on travaille sur des grands échantillons,
la probabilité pour qu’une réalisation de ˆΘ diffère sensiblement de la vraie valeur de θ est faible.
4.1.3 Comparaison d’estimateurs
Le staticien est souvent confronté au problème de choisir entre plusieurs estimateurs potentiels d’un même
paramètre. La démarche utilisée pour comparer deux (ou plusieurs) estimateurs consiste à raisonner sur ce qu’on
appelle l’écart quadratique moyen : indicateur utilisé pour mesurer la précision d’un estimateur.
Définition 1 : Soit ˆΘ un estimateur de θ. On appelle écart quadratique moyen (EQM ) de ˆΘ le réel défini par :
EQM
³
ˆΘ
´
= E
³
ˆΘ − θ
´2
De deux estimateurs ˆΘ1 et ˆΘ2 de θ, on utilisera préférentiellement celui dont l’écart quadratique moyen est le
plus faible.
Propriété de L’écart quadratique moyen
EQM
³
ˆΘ
´
= E
³
ˆΘ − θ
´2
= V
³
ˆΘ
´
+
h
B
³
ˆΘ
´i2
En effet : EQM
³
ˆΘ
´
= E
³
ˆΘ − θ
´2
= E
h
ˆΘ − E
³
ˆΘ
´
+ E
³
ˆΘ
´
− θ
i2
= E
h³
ˆΘ − E
³
ˆΘ
´´
+
³
E
³
ˆΘ
´
− θ
´i2
= E
∙³
ˆΘ − E
³
ˆΘ
´´2
+ 2
³
ˆΘ − E
³
ˆΘ
´´ ³
E
³
ˆΘ
´
− θ
´
+
³
E
³
ˆΘ
´
− θ
´2
¸
= E
³
ˆΘ − E
³
ˆΘ
´´2
| {z }
V ( ˆΘ)
+ 2
³
E
³
ˆΘ
´
− θ
´
E
³
ˆΘ − E
³
ˆΘ
´´
| {z }
0
+
³
E
³
ˆΘ
´
− θ
´2
| {z }
[B( ˆΘ)]2
= V
³
ˆΘ
´
+
h
B
³
ˆΘ
´i2
42

65. Définition 2 (Efficacité relative) : Soient ˆΘ1 et ˆΘ2 deux estimateurs sans biais de θ. On dit que ˆΘ1 est plus
efficace que ˆΘ2 lorsque :
V
³
ˆΘ1
´
< V
³
ˆΘ2
´
L’efficacité d’un estimateur est une notion relative qui conduit à se demander s’il existe un estimateur plus
efficace que tous les autres (efficacité absolue).
Un théorème dit de Frechet-Darmois-Cramer-Rao (F.D.C.R), montre qu’il existe une borne inférieure pour
l’ensemble des variances des estimateurs sans biais de θ. Ce théorème s’appuie sur la notion de l’information de
Fisher.
4.1.4 Information de Fisher
Définition : Soit (X1, X2, . . . , Xn) un EAS iid de taille n, issu d’une population X de paramètre θ inconnu. On
appelle quantité d’information de Fisher apportée par la réalisation (x1, x2, . . . , xn) de l’échantillon (X1, X2, . . . , Xn)
sur le paramètre θ, le nombre réel positif définie par :
In (θ) = E
"µ
∂LogL(X1, X2, . . . , Xn, θ)
∂θ
¶2
#
où L(x1, x2, . . . , xn, θ) est la fonction de vraisemblance du paramètre θ sur l’échantillon (X1, X2, . . . , Xn) définie
par :
L(x1, x2, . . . , xn, θ) =
nQ
i=1
f(xi, θ)
f(x, θ) est la ddp de la variable aléatoire X.
Théorème 1 : Soit (X1, X2, . . . , Xn) un EAS iid de taille n, issu d’une population X de paramètre θ inconnu.
Si X(Ω) ne dépend pas de θ, alors :
In (θ) = nI1 (θ) avec I1 (θ) = E
"µ
∂Logf(X, θ)
∂θ
¶2
#
L’information apportée par la réalisation de l’échantillon sur le paramètre θ est égale à n fois l’information
apportée par une réalisation de la variable aléatoire X (c.-à-d. par une seule observation).
Théorème 2 (Formule pratique pour le calcul de la quantité d’information de Fisher)
Soit (X1, X2, . . . , Xn) un EAS iid de taille n, issu d’une population X de paramètre θ inconnu. Si X(Ω) ne
dépend pas de θ, alors :
1. La quantité d’information de Fisher fournie par une réalisation de la variable aléatoire X sur le paramètre θ
est :
I1 (θ) = −E
∙
∂2
Logf(X, θ)
∂θ2
¸
2. La quantité d’information de Fisher fournie par une réalisation de l’échantillon (X1, X2, . . . , Xn) sur le para-
mètre θ est :
In (θ) = −E
∙
∂2
LogL(X1, X2, . . . , Xn, θ)
∂θ2
¸
Exemple :
Soit (X1, X2, . . . , Xn) un EAS iid de taille n, issu d’une population de Poisson de paramètre λ inconnu. Calculer,
de deux manières différentes, la quantité d’information de Fisher In(λ).
X Ã P(λ) ⇒ f(x, λ) = P(X = x, λ) =
(
e−λ λx
x!
si x ∈ N
0 sinon
et E(X) = V (X) = λ
1`ere
méthode :
On a X(Ω) = N ne dépend pas de λ ⇒ In (λ) = nI1 (λ)
où I1 (λ) = −E
∙
∂2
Logf(X, λ)
∂λ2
¸
avec Logf(x, λ) = Log
µ
e−λ λx
x!
¶
= −λ + xLogλ − Log (x!)
⇒
∂Logf(x, λ)
∂λ
=
∂ (−λ + xLogλ − Log (x!))
∂λ
= −1 +
x
λ
43

66. ⇒
∂2
Logf(x, λ)
∂λ2 =
∂
³
−1 +
x
λ
´
∂λ
= −
x
λ2
⇒ I1 (λ) = −E
∙
∂2
Logf(X, λ)
∂λ2
¸
= −E
µ
−
X
λ2
¶
=
1
λ2 E(X) =
λ
λ2 =
1
λ
⇒ In (λ) = nI1 (λ) =
n
λ
2`eme
méthode :
In (λ) = −E
∙
∂2
LogL(X1, X2, . . . , Xn, λ)
∂λ2
¸
avec LogL(x1, x2, . . . , xn, λ) = Log
∙ nQ
i=1
f(xi, λ)
¸
=
nP
i=1
Log (f(xi, λ)) =
nP
i=1
Log
µ
e−λ λxi
(xi)!
¶
=
nP
i=1
(−λ + xiLogλ − Log [(xi)!])
= −nλ + Logλ
nP
i=1
xi −
nP
i=1
Log [(xi)!]
⇒
∂LogL(x1, x2, . . . , xn, λ)
∂λ
= −n +
Pn
i=1 xi
λ
⇒
∂2
LogL(x1, x2, . . . , xn, λ)
∂λ2 = −
Pn
i=1 xi
λ2
⇒ In (λ) = −E
∙
∂2
LogL(X1, X2, . . . , Xn, λ)
∂λ2
¸
= −E
µ
−
Pn
i=1 Xi
λ2
¶
=
1
λ2
Pn
i=1 E(Xi) =
nλ
λ2 =
n
λ
4.1.5 Efficacité absolue
Théorème de F.D.C.R :
Si X(Ω) est indépendant du paramètre à estimer θ, alors pour tout estimateur ˆΘ sans biais de θ on a :
V
³
ˆΘ
´
≥
1
In (θ)
Cette inégalité est généralement appelée l’inégalité de Cramer-Rao.
La quantité
1
In (θ)
est la borne inférieure de F.D.C.R.
Définition :
Un estimateur sans biais ˆΘ est dit efficace si sa variance est égale à la borne inférieure de F.D.C.R. :
V
³
ˆΘ
´
=
1
In (θ)
4.2 Les méthodes d’estimation ponctuelle
Il existe plusieurs procédés permettant de construire concrètement des estimateurs. Les méthodes d’estimation
ponctuelle les plus courantes sont :
— La méthode du maximum de vraisemblance (MV).
— La méthode des moments (MM).
— La méthode des moindres carrées ordinaires (MCO).
Nous exposerons uniquement les deux premières.
4.2.1 L’estimation par la méthode du maximum de vraisemblance
Soit (X1, X2, . . . , Xn) un EAS iid de taille n, issu d’une population X de densité de probabilité f(X, θ), θ
étant le paramètre inconnu qu’on cherche à estimer. La méthode du maximum de vraisemblance (MV) consiste
à estimer θ en choisissant la valeur ˆθ qui maximise la fonction de vraisemblance du paramètre θ sur l’échantillon
(X1, X2, . . . , Xn). Cette méthode se résume par les quatre étapes suivantes :
1. Expliciter la fonction de vraisemblance du paramètre θ estimer définie par :
L(x1, x2, . . . , xn, θ) =
nQ
i=1
f(xi, θ)
44

67. 2. Appliquer la transformation logarithmique à la fonction de vraisemblance :
LogL(x1, x2, . . . , xn, θ) = Log
∙ nQ
i=1
f(xi, θ)
¸
=
nP
i=1
Log (f(xi, θ))
3. Appliquer la dérivée par rapport au paramètre à estimer à la fonction Log-vraisemblance et résoudre l’équation
d’inconnue θ :
∂LogL(x1, x2, . . . , xn, θ)
∂θ
= 0 ⇒ θ = ˆθ
4. Vérifier la condition :
∂2
LogL(x1, x2, . . . , xn, θ)
∂θ2
¯
¯
¯
¯
θ=ˆθ
< 0
Si cette dernière est satisfaite, alors l’estimateur du MV est celui fourni à l’étape 3
³
ˆθMV = ˆθ
´
.
Exemples :
1. Estimation du paramètre λ d’une loi de Poisson P(λ)
Soit (X1, X2, . . . , Xn) un EAS iid de taille n, issu d’une population de Poisson de paramètre λ inconnu.
Estimer le paramètre λ par la méthode du maximum de vraisemblance.
1`ere
étape : L(x1, x2, . . . , xn, λ) =
nQ
i=1
f(xi, λ) =
nQ
i=1
∙
e−λ λxi
(xi)!
¸
.
2`eme
étape : LogL(x1, x2, . . . , xn, λ) =
nP
i=1
Log
µ
e−λ λxi
(xi)!
¶
= −nλ + Logλ
nP
i=1
xi −
nP
i=1
Log [(xi)!]
3`eme
étape :
∂LogL(x1, x2, . . . , xn, λ)
∂λ
= −n +
Pn
i=1 xi
λ
= 0 ⇒ ˆλ =
1
n
Pn
i=1 xi = x.
4`eme
étape :
∂2
LogL(x1, x2, . . . , xn, λ)
∂λ2
¯
¯
¯
¯
λ=ˆλ
= −
Pn
i=1 xi
ˆλ
2 = −
nx
x2 = −
n2
Pn
i=1 xi
< 0 ⇒ ˆλMV = X .
2. Estimation des paramètres m et σ2
d’une loi normale
Soit (X1, X2, . . . , Xn) un EAS iid de taille n, issu d’une population normale de paramètres m et σ2
inconnus.
Déterminer les estimateurs du MV de m et σ2
.
On a X Ã N
¡
m, σ2
¢
⇒ ∀x ∈ R, f(x, m, σ2
) =
1
σ
√
2Π
e
−
1
2
x − m
σ
2
(X1, X2, . . . , Xn) un EAS iid ⇒
⎧
⎪⎨
⎪⎩
Les Xi sont indépendantes
Xi à N
¡
m, σ2
¢
, ∀i : 1 . . . n ⇒ f(xi, m, σ2
) =
1
σ
√
2Π
e
−
1
2
xi − m
σ
2
1`ere
étape : L(x1, x2, . . . , xn, m, σ2
) =
nQ
i=1
f(xi, m, σ2
) =
nQ
i=1
⎡
⎢
⎣
1
σ
√
2Π
e
−
1
2
xi − m
σ
2
⎤
⎥
⎦
2`eme
étape : LogL(x1, x2, . . . , xn, m, σ2
) =
nP
i=1
Log
⎛
⎜
⎝
1
σ
√
2Π
e
−
1
2
xi − m
σ
2
⎞
⎟
⎠
= −nLogσ − nLog
√
2Π −
1
2σ2
nP
i=1
(xi − m)
2
3`eme
étape :
∂LogL(x1, x2, . . . , xn, m, σ2
)
∂m
=
1
σ2
nP
i=1
(xi − m) = 0 ⇒ ˆm =
1
n
Pn
i=1 xi = x.
∂LogL(x1, x2, . . . , xn, m, σ2
)
∂σ2
= −
n
2
1
σ2
+
1
2σ4
nP
i=1
(xi − ˆm)2
= 0 ⇒ ˆσ2
=
1
n
nP
i=1
(xi − ˆm)2
⇒ ˆσ2
=
1
n
nP
i=1
(xi − x)
2
⇒ ˆσ2
= s02
4`eme
étape : X et S02
seront les estimateurs du MV de m et σ2
si la forme quadratique associée à la ma-
trice hessienne des dérivées secondes est définie négatives (conditions du second ordre pour l’existence d’un
maximum).
45

68. 4.2.2 L’estimation par la méthode des moments
Le principe de la méthode des moments consiste à égaliser les moments théoriques d’une distribution de proba-
bilité f(x, θ) aux moments empiriques afin d’estimer le paramètre inconnu θ. Dans le cas où on a une distribution à
k paramètres inconnus θ1, θ2, . . . , θk (par exemple la loi normale et la loi gamma : 2 paramètres inconnus respective-
ment
¡
m, σ2
¢
et (α, θ)), l’estimation de ces paramètres par la méthode des moments consiste à résoudre le système
qui égalise les k premiers moments théoriques de la population aux moments correspondant de l’échantillon :
⎧
⎪⎪⎪⎨
⎪⎪⎪⎩
m1 = m∗
1
m2 = m∗
2
...
mk = m∗
k
système à k équations et k inconnus
où mk = E(Xk
) est le moment théorique (de la population) d’ordre k
et m∗
k =
1
n
nP
i=1
Xk
i est le moment empirique (de l’échantillon) d’ordre k
Exemple :
Soit (X1, X2, . . . , Xn) un EAS iid de taille n, issu d’une population X qui suit la loi gamma de paramètres α
et θ inconnues. Estimer α et θ par la méthode des moments.
On sait que si X Ã γ (α, θ) ⇒
⎧
⎪⎨
⎪⎩
m1 = E(X) =
α
θ
m2 = E(X2
) =
α (α + 1)
θ2
Les moments empiriques sont donnés par :
⎧
⎪⎪⎨
⎪⎪⎩
m∗
1 =
1
n
nP
i=1
Xi = X
m∗
2 =
1
n
nP
i=1
X2
i
Notre système est donc :
½
m1 = m∗
1
m2 = m∗
2
⇔
⎧
⎪⎪⎨
⎪⎪⎩
α
θ
=
1
n
nP
i=1
Xi = X (1)
α (α + 1)
θ2 =
1
n
nP
i=1
X2
i (2)
(1) ⇒ α = θX. En remplaçant dans (2) on a :
(2) ⇒
¡
θX
¢2
+ θX
θ2 =
1
n
Pn
i=1 X2
i ⇔
X
θ
=
1
n
Pn
i=1 X2
i − X
2
⇔ θ =
X
1
n
Pn
i=1 X2
i − X
2
⇔ θ =
nX
Pn
i=1 X2
i − nX
2 =
nX
Pn
i=1
¡
Xi − X
¢2 =
nX
nS02
=
X
S02
(1) ⇒ α = θX =
µ
X
S0
¶2
Ainsi ˆαMM =
µ
X
S0
¶2
ˆθMM =
X
S02
46

69. 5 L’estimation par intervalle de confiance
Les expérimentateurs préfèrent donner, au lieu d’une estimation ponctuelle ˆθ du paramètre inconnu θ, un
intervalle dans lequel ils ont la quasi-certitude de cerner la vraie valeur de θ. Cet intervalle est appelé intervalle de
confiance de θ.
La quasi-certitude, dont dépend la largeur de l’intervalle, est mesurée par une probabilité appelée niveau de
confiance ou coefficient de sécurité. On ne donnera jamais un intervalle de confiance sans l’accompagner du niveau
de confiance choisi.
5.1 Définition
Un intervalle de confiance pour le paramètre θ inconnu, de niveau de confiance (1 − α) ∈ ]0, 1[, est un intervalle
qui a la probabilité 1 − α de contenir la vraie valeur du paramètre θ :
IC(1−α) (θ) = [L1, L2] ⇔ P (L1 ≤ θ ≤ L2) = 1 − α
5.2 Principe de construction de l’intervalle de confiance
La construction d’un intervalle de confiance pour un paramètre inconnu θ comporte 5 étapes :
1. Choisir un niveau de confiance 1 − α (α : seuil de signification ou risque).
2. Déterminer la distribution d’échantillonnage de la statistique à utiliser : T = f
³
ˆΘ, θ
´
à L.(f est dite fonction
pivotale). L’expression de T ne doit contenir qu’un seul inconnu : le paramètre θ
3. Présenter l’équation qui permet de déterminer l’intervalle de confiance :
P
³
k1 ≤ f
³
ˆΘ, θ
´
≤ k2
´
= 1 − α
4. Déterminer les 2 quantiles k1 et k2 à partir de la table statistique qui correspond à la loi de probabilité de
T = f
³
ˆΘ, θ
´
. k1 et k2 doivent vérifier :
P
³
f
³
ˆΘ, θ
´
< k1
´
= P
³
f
³
ˆΘ, θ
´
> k2
´
=
α
2
5. Résoudre l’inéquation k1 ≤ f
³
ˆΘ, θ
´
≤ k2 afin de déterminer l’intervalle de confiance du paramètre inconnu
θ, satisfaisant la relation suivante :
P
³
g1
³
ˆΘ
´
≤ θ ≤ g2
³
ˆΘ
´´
= 1 − α
et on a finalement : IC(1−α) (θ) =
h
L1 = g1
³
ˆΘ
´
, L2 = g2
³
ˆΘ
´i
5.2.1 Intervalle de confiance pour la moyenne
Soit (X1, X2, . . . , Xn) un EAS iid de taille n, issu d’une population X de moyenne inconnue m et de variance
σ2
.
a/ Cas où σ2
est connue : (X Ã N
¡
m, σ2
¢
et nqcq ) ou (X Ã Lqcq
¡
m, σ2
¢
et n ≥ 30)
1. Soit 1 − α le niveau de confiance choisi.
2. On sait que dans les deux cas où :
X Ã N
¡
m, σ2
¢
et nqcq
X Ã Lqcq
¡
m, σ2
¢
et n ≥ 30
¾
on a X Ã N(m,
σ2
n
) ⇒
X − m
σ/
√
n
à N(0, 1)
Ainsi, pour déterminer un intervalle de confiance pour la moyenne dans le cas où σ2
est connue, on retient la
statistique T = f
³
ˆΘ, θ
´
= f
¡
X, m
¢
=
X − m
σ/
√
n
à N(0, 1).
3. L’équation qui permet de déterminer IC(1−α) (m) est donc : P
µ
k1 ≤
X − m
σ/
√
n
≤ k2
¶
= 1 − α.
47

70. 4. P
³
k1 ≤ X−m
σ/
√
n
≤ k2
´
= 1 − α ⇒ k1 = Zα
2
= −Z1− α
2
et k2 = Z1− α
2
z
1 α− 2
α
2
α
1 21k Z α= − − 2 21k Z α= −
5. −Z1− α
2
≤
X − m
σ/
√
n
≤ Z1− α
2
⇔ −Z1− α
2
×
σ
√
n
≤ X − m ≤ Z1− α
2
×
σ
√
n
⇔ −X − Z1− α
2
×
σ
√
n
≤ −m ≤ −X + Z1− α
2
×
σ
√
n
⇔ X − Z1− α
2
×
σ
√
n
≤ m ≤ X + Z1− α
2
×
σ
√
n
⇒ P
µ
−Z1− α
2
≤
X − m
σ/
√
n
≤ Z1− α
2
¶
= P
⎛
⎜
⎜
⎜
⎜
⎝
X − Z1− α
2
×
σ
√
n
| {z }
L1=g1(X)
≤ m ≤ X + Z1− α
2
×
σ
√
n
| {z }
L2=g2(X)
⎞
⎟
⎟
⎟
⎟
⎠
= 1 − α
⇒ IC(1−α) (m) =
∙
X − Z1− α
2
×
σ
√
n
, X + Z1− α
2
×
σ
√
n
¸
=
∙
X ± Z1− α
2
×
σ
√
n
¸
b/ Cas où σ2
est inconnue : X Ã N
¡
m, σ2
¢
1. Soit 1 − α le niveau de confiance choisi.
2. σ étant inconnu, nous ne pouvons plus utiliser la statistique
X − m
σ/
√
n
pour construire un intervalle de confiance
pour la moyenne. Cependant, on sait que
X − m
S/
√
n
à T (n − 1) . Dans l’expression de cette dernière statistique,
le seul inconnu est m (S est l’écart-type échantillonnale corrigé et peut être calculé à partir de l’échantillon
extrait).
Ainsi, pour déterminer un intervalle de confiance pour la moyenne, dans le cas où σ2
est inconnue, on retient
la statistique
X − m
S/
√
n
à T (n − 1) .
3. L’équation qui permet de déterminer IC(1−α) (m) est donc : P
µ
k1 ≤
X − m
S/
√
n
≤ k2
¶
= 1 − α.
4. P
µ
k1 ≤
X − m
S/
√
n
≤ k2
¶
= 1 − α ⇒ k1 = T
(n−1)
α
2
= −T
(n−1)
1− α
2
et k2 = T
(n−1)
1− α
2
t
1 α− 2
α
2
α
( )1
1
21
n
k T α
−
= −
−
( )1
2
21
n
k T α
−
=
−
5. ⇒ P
µ
−T
(n−1)
1− α
2
≤
X − m
S/
√
n
≤ T
(n−1)
1− α
2
¶
= P
µ
X − T
(n−1)
1− α
2
×
S
√
n
≤ m ≤ X + T
(n−1)
1− α
2
×
S
√
n
¶
= 1 − α
⇒ IC(1−α) (m) =
∙
X − T
(n−1)
1− α
2
×
S
√
n
, X + T
(n−1)
1− α
2
×
S
√
n
¸
=
∙
X ± T
(n−1)
1− α
2
×
S
√
n
¸
48

71. Remarque : Lorsque n > 30, la distribution de Student à (n − 1) degrés de liberté converge vers la loi normale
centrée réduite (T
(n−1)
1− α
2
' Z1− α
2
). Ainsi, dans le cas où σ2
est inconnue, si la taille de l’échantillon est grande
(n > 30), l’intervalle de confiance pour m au niveau 1 − α devient :
IC(1−α) (m) =
∙
X − Z1− α
2
×
S
√
n
, X + Z1− α
2
×
S
√
n
¸
5.2.2 Intervalle de confiance pour la variance d’une loi normale
Soit (X1, X2, . . . , Xn) un EAS iid de taille n, issu d’une population X normale, de moyenne m et de variance
inconnue σ2
.
a/ Cas où m est inconnue
1. Soit 1 − α le niveau de confiance choisi.
2. Dans le cas où m est inconnue, la statistique à utiliser pour déterminer un intervalle de confiance pour la
variance est
(n − 1) S2
σ2
à χ2
(n − 1) .
3. L’équation qui permet de déterminer IC(1−α)
¡
σ2
¢
est : P
µ
k1 ≤
(n − 1) S2
σ2
≤ k2
¶
= 1 − α.
4. P
µ
k1 ≤
(n − 1) S2
σ2
≤ k2
¶
= 1 − α ⇒ k1 = χ2
α
2
(n − 1) et k2 = χ2
1− α
2
(n − 1)
2
2
2
1( )nk αχ −=
x
1 α−
2
α
2
α
2
2
2 1
1( )nk αχ −
−=
5. P
µ
χ2
α
2
(n − 1) ≤
(n − 1) S2
σ2
≤ χ2
1− α
2
(n − 1)
¶
= 1 − α ⇔ P
Ã
χ2
α
2
(n − 1)
(n − 1) S2
≤
1
σ2
≤
χ2
1− α
2
(n − 1)
(n − 1) S2
!
= 1 − α
⇔ P
Ã
(n − 1) S2
χ2
1− α
2
(n − 1)
≤ σ2
≤
(n − 1) S2
χ2
α
2
(n − 1)
!
= 1 − α
⇔ IC(1−α)
¡
σ2
¢
=
"
(n − 1) S2
χ2
1− α
2
(n − 1)
,
(n − 1) S2
χ2
α
2
(n − 1)
#
b/ Cas où m est connue
1. Soit 1 − α le niveau de confiance choisi.
2. Dans le cas où m est connue, pour déterminer un intervalle de confiance pour la variance, on utilise la
statistique
nS02
0
σ2
à χ2
(n) avec S02
0 =
1
n
Pn
i=1 (Xi − m)
2
En effet, X Ã N
¡
m, σ2
¢
et (X1, X2, . . . , Xn) iid de X ⇒ Xi à N
¡
m, σ2
¢
∀i : 1 . . . n
⇒
Xi − m
σ
à N (0, 1) ⇒
µ
Xi − m
σ
¶2
à χ2
(1) ⇒
1
σ2
nP
i=1
(Xi − m)
2
| {z }
nS02
0
à χ2
(n)
3. L’équation qui permet de déterminer IC(1−α)
¡
σ2
¢
est : P
µ
k1 ≤
nS02
0
σ2
≤ k2
¶
= 1 − α.
49

72. 4. P
µ
k1 ≤
nS02
0
σ2
≤ k2
¶
= 1 − α ⇒ k1 = χ2
α
2
(n) et k2 = χ2
1− α
2
(n)
2
2
2
( )nk αχ=
x
1 α−
2
α
2
α
2
2
2 1
( )nk αχ −
=
5. P
µ
χ2
α
2
(n) ≤
nS02
0
σ2
≤ χ2
1− α
2
(n)
¶
= 1 − α ⇔ P
Ã
nS02
0
χ2
1− α
2
(n)
≤ σ2
≤
nS02
0
χ2
α
2
(n)
!
= 1 − α
⇔ IC(1−α)
¡
σ2
¢
=
"
nS02
0
χ2
1− α
2
(n)
,
nS02
0
χ2
α
2
(n)
#
5.2.3 Intervalle de confiance pour une proportion
Soit (X1, X2, . . . , Xn) un EAS iid de taille n, assez élevée (n ≥ 30), issu d’une population X de Bernoulli de
paramètre p inconnu. La construction d’un IC (p) passe par les étapes suivantes :
1. Soit 1 − α le niveau de confiance choisi.
2. Pour déterminer un intervalle de confiance pour la proportion inconnue p, on retient la statistique :
F − p
r
p (1 − p)
n
à N (0, 1) , où F =
1
n
nX
i=1
Xi est la proportion échantillonnale
3. L’équation qui permet de déterminer IC(1−α) (p) est : P
⎛
⎝k1 ≤
F − p
q
p(1−p)
n
≤ k2
⎞
⎠ = 1 − α
4. P
⎛
⎝k1 ≤
F − p
q
p(1−p)
n
≤ k2
⎞
⎠ = 1 − α ⇒ k1 = −Z1− α
2
et k2 = Z1− α
2
5. P
⎛
⎝−Z1− α
2
≤
F − p
q
p(1−p)
n
≤ Z1− α
2
⎞
⎠ = 1 − α ⇔ P
Ã
F − Z1− α
2
r
p (1 − p)
n
≤ p ≤ F + Z1− α
2
r
p (1 − p)
n
!
IC(1−α) (p) =
"
F − Z1− α
2
r
p (1 − p)
n
, F + Z1− α
2
r
p (1 − p)
n
#
On remarque que les bornes de cet intervalle contiennent la valeur inconnue p. Pour résoudre cette difficulté, il
suffit de remplacer p par son estimateur F dans les bornes de cet intervalle, ce qui conduit à l’intervalle de confiance
suivant :
IC(1−α) (p) =
"
F − Z1− α
2
r
F (1 − F)
n
, F + Z1− α
2
r
F (1 − F)
n
#
50

73. K&M http ://stat.fateback.com
Chapitre 4
Les tests d’hypothèses paramétriques
1 Définitions
1.1 Hypothèse statistique
On appelle hypothèse statistique une proposition concernant la loi de probabilité d’une variable aléatoire X ou
un ou plusieurs paramètres de cette loi.
— Lorsque la proposition concerne la loi de probabilité de X : on parle d’hypothèse non paramétrique.
— Lorsque la proposition porte sur un ou plusieurs paramètres d’une loi : on parle d’hypothèse paramétrique.
Dans le présent cours, on s’intéressera uniquement aux hypothèses paramétriques, c.-à-d. aux hypothèses qui
concernent les paramètres d’une loi.
1.2 Test statistique
On appelle un test statistique une règle ou procédure de décision qui nous permet, au vu de l’échantillon,
d’accepter ou rejeter l’hypothèse statistique.
1.3 Les étapes d’un test
1.3.1 Formulation des hypothèses
La première étape d’un test consiste à formuler deux hypothèses alternatives désignées par H0 et H1, entre
lesquelles le choix sera réalisé au vu d’une réalisation (x1, x2, . . . , xn) de l’échantillon.
Exemple : le niveau moyen des revenus des ménages de la ville de Sfax, noté m, est-il égal ou différent de celui
de l’ensemble des ménages tunisiens, noté m0 ?
Cette question est donc un choix entre deux hypothèses :
H0 : m = m0 le revenu moyen des ménages de la ville de Sfax est égal à m0
H1 : m 6= m0 le revenu moyen de la ville de Sfax diffère de m0
L’hypothèse H0 s’appelle hypothèse nulle, hypothèse de base ou encore hypothèse privilégiée. Elle est construite
à partir d’une idée à priori sur la valeur du paramètre ; c’est l’hypothèse qu’on souhaite retenir tant qu’elle n’est
pas infirmée par l’expérience.
L’hypothèse H1 s’appelle hypothèse adverse, hypothèse alternative ou encore contre hypothèse ; c’est l’hypothèse
qu’on va admettre si on décide de rejeter l’hypothèse de base H0.
La formulation de H0 dépend du problème étudié. Ainsi, dans notre exemple :
— Si l’étude des revenus ne vise qu’à mettre en évidence une différence entre la ville de Sfax et la norme tunisienne,
alors H1 postulera une différence entre le revenu moyen m de la ville de Sfax et la norme m0 : H1 : m 6= m0
— Si parcontre, l’étude vise à valider l’idée que le pouvoir d’achat dans la ville de Sfax est supérieur (respecti-
vement inférieur) à la norme tunisienne, alors H1 : m > m0 (respectivement m < m0).
L’énoncé des hypothèses est un point capital dans la théorie des tests. La manière dont les hypothèses sont
formulées donne lieu à deux catégories de tests :
Les tests simples : il s’agit de tester une hypothèse simple H0 contre une hypothèse simple H1.
½
H0 : θ = θ0
H1 : θ = θ1 (avec θ1 6= θ0)
Les tests multiples : il s’agit de tester une hypothèse simple H0 contre une hypothèse multiple H1. Ces tests se
présentent généralement sous l’une des formes suivantes :
a)
½
H0 : θ = θ0
H1 : θ > θ0
b)
½
H0 : θ = θ0
H1 : θ < θ0
c)
½
H0 : θ = θ0
H1 : θ 6= θ0 ⇔ (θ > θ0 ou θ < θ0)
Dans cette gamme de tests multiples, on distingue les tests unilatéraux (unilatéral à droite (a) ou unilatéral à
gauche (b)) et les tests bilatéraux (c).
51

74. 1.3.2 Acceptation d’un risque d’erreur
Effectuer l’un des tests d’hypothèses ci-dessus consiste à confronter deux hypothèses H0 et H1. Deux décisions
peuvent être prises :
D0 : accepter H0 ou D1 : rejeter H0 (donc accepter H1)
Le test conduit donc à 4 situations possibles dont deux sont entachées d’erreurs :
état de la nature
Décision
D0 : accepter H0
D1 : rejeter H0
H0 vraie H0 fausse (H1 vraie)
Bonne décision
erreur de 1ère
espèce
erreur de 2ème
espèce
Bonne décision
— Erreur de 1`ere
espèce : c’est le fait de rejeter à tort l’hypothèse de base H0 ⇔ (rejeter H0 / H0 est vraie)
⇔ (D1 / H0 est vraie) ⇔ (accepter H1 / H0 est vraie).
A cette erreur de 1`ere
espèce est associé un risque noté α défini par :
α = risque de commettre l’erreur de 1`ere
espèce
= P(rejeter à tort H0) = P(rejeter H0 / H0 est vraie)
α est appelé risque de 1`ere
espèce ou seuil de signification du test.
1 − α est appelé niveau de confiance du test (1 − α = P(accepter H0 / H0 est vraie)).
— Erreur de 2`eme
espèce : c’est le fait d’accepter à tort l’hypothèse de base H0 ⇔ (accepter H0 / H1 est vraie)
⇔ (D0 / H1 est vraie) ⇔ (rejeter H1 / H1 est vraie).
A cette erreur de 2`eme
espèce est associé un risque noté β défini par :
β = risque de commettre l’erreur de 2`eme
espèce
= P(accepter à tort H0) = P(accepter H0 / H1 est vraie)
β est appelé risque de 2`eme
espèce.
1 − β est appelé puissance du test : c’est la probabilité de rejeter avec raison H0
1 − β = P(rejeter H0 / H1 est vraie)
N.B : α et β ne peuvent pas être contrôlées simultanément puisqu’ils varient en sens contraire. L’hypothèse H0
jouant un rôle particulier dans le test, on ne doit pas la rejeter sans raison valable : On fixe donc le risque α à un
niveau raisonnable (1%, 5% ou 10%) et on essaye de minimiser β (donc de maximiser la puissance du test).
1.3.3 Choix d’une variable de décision et détermination de la région critique du test
Pour tester l’hypothèse H0 on utilise généralement une statistique, fonction de l’échantillon aléatoire ˆΘ =
f (X1, X2, . . . , Xn) dont la loi de probabilité dépend du paramètre θ sur lequel porte le test d’hypothèses. Ainsi,
pour réaliser un test sur la moyenne d’une loi normale, on pourra s’appuyer sur la moyenne X de l’échantillon. Le
choix de la meilleure variable de décision a été résolu théoriquement par les staticiens Neyman et Pearson dans une
série d’articles célébres parus de 1933 à 1938.
Théorème de Neyman et Pearson
Soit (X1, X2, . . . , Xn) un EAS iid de taille n, issu d’une population X dont la densité de probabilité f (x, θ)
dépend d’un paramètre inconnu θ, et soit à tester le corps d’hypothèses suivant :
½
H0 : θ = θ0
H1 : θ = θ1
Le test unifomément le plus puissant (UPP) au niveau de signification α est celui dont la région critique RC est
de la forme :
RC =
½
(x1, x2, . . . , xn) ∈
−→
X (Ω)
Á
L0 (x1, x2, . . . , xn, θ0)
L1 (x1, x2, . . . , xn, θ1)
< k
¾
52

75. k étant une constante strictement positive et L (x1, x2, . . . , xn, θ) désignant la vraisemblance du paramètre θ sur
l’échantillon (X1, X2, . . . , Xn) .
La région critique RC est par définition la région de rejet de l’hypothèse nulle H0. C’est l’ensemble des réalisations
de l’échantillon aléatoire (X1, X2, . . . , Xn) pour lesquelles on rejette H0 (c’est également l’ensemble des réalisations
de ˆΘ pour lesquelles on prend la décision de rejeter H0).
Bien évidement, l’ensemble des réalisations de (X1, X2, . . . , Xn) pour lesquelles on accepte H0 défini la région
d’acceptation RA. (c’est le complémentaire de RC par rapport à l’ensemble de toutes les réalisations possibles de
l’EA (X1, X2, . . . , Xn) :
−→
X (Ω))
Le calcul des bornes de la région critique passe par l’expression du risque α en fonction de RC :
α = P(rejeter H0|sous H0) = P((X1, X2, . . . , Xn) ∈ RC|sous H0)
1.4 Observation d’un échantillon et prise de décision
Le test ayant été construit et une règle de décision ayant été formulée (détermination de RC et RA), pour choisir
entre les deux hypothèses H0 et H1, il suffit d’observer un échantillon et de calculer la valeur de la variable de
décision ˆΘ dans cet échantillon. Selon que cette valeur appartienne à RA ou à RC on accepte ou on rejette H0.
2 Tests sur la moyenne d’une loi normale
2.1 Test simple
On étudie sur la population mère un caractère X distribuée selon la loi normale
¡
m, σ2
¢
et on désire effectuer
au niveau de signification α un test sur le paramètre inconnu m.
½
H0 : m = m0
H1 : m = m1 (m1 6= m0)
Selon le théorème de Neyman et Pearson, le test UPP de niveau de signification α est celui dont la région
critique est définie par : RC =
½
(x1, x2, . . . , xn)
Á
L0 (x1, x2, . . . , xn, θ0)
L1 (x1, x2, . . . , xn, θ1)
< k
¾
k > 0.
La vraisemblance de l’échantillon aléatoire de taille n est :
L (x1, x2, . . . , xn, m) =
nQ
i=1
f(xi, m) avec f(xi, m) =
1
σ
√
2Π
e
−
1
2
xi − m
σ
2
est la ddp de la loi normale
⇒
⎧
⎪⎪⎪⎪⎪⎨
⎪⎪⎪⎪⎪⎩
L (x1, x2, . . . , xn, m0) =
nQ
i=1
f(xi, m0) =
nQ
i=1
1
σ
√
2Π
e
−
1
2
xi − m0
σ
2
L (x1, x2, . . . , xn, m1) =
nQ
i=1
f(xi, m1) =
nQ
i=1
1
σ
√
2Π
e
−
1
2
xi − m1
σ
2
⇒
L0 (x1, x2, . . . , xn, θ0)
L1 (x1, x2, . . . , xn, θ1)
=
nQ
i=1
1
σ
√
2Π
exp
Ã
−
1
2
µ
xi − m0
σ
¶2
!
nQ
i=1
1
σ
√
2Π
exp
Ã
−
1
2
µ
xi − m1
σ
¶2
! =
nQ
i=1
"
exp
Ã
−
1
2
µ
xi − m0
σ
¶2
+
1
2
µ
xi − m1
σ
¶2
!#
= exp
Ã
nP
i=1
"
− (xi − m0)
2
+ (xi − m1)
2
2σ2
#!
= exp
Ã
nP
i=1
"
−2xi (m1 − m0) +
¡
m2
1 − m2
0
¢
2σ2
#!
= exp
Ã
−2nx (m1 − m0) + n
¡
m2
1 − m2
0
¢
2σ2
!
L0 (x1, x2, . . . , xn, θ0)
L1 (x1, x2, . . . , xn, θ1)
< k ⇔
−2nx (m1 − m0) + n
¡
m2
1 − m2
0
¢
2σ2
< Logk
⇔ −2nx (m1 − m0) + n
¡
m2
1 − m2
0
¢
< 2σ2
Logk
⇔ x (m1 − m0) >
n
¡
m2
1 − m2
0
¢
− 2σ2
Logk
2n
= k0
A ce niveau, deux cas peuvent se présenter : a) m1 > m0 ou b) m1 < m0
53

76. a) m1 > m0 b) m1 < m0
(m1 − m0) > 0 ⇒ x >
k0
m1 − m0
= c. (m1 − m0) < 0 ⇒ x <
k0
m1 − m0
= c.
c est une constante appelée seuil critique
Forme de la région critique
RC =
n
(x1, x2, . . . , xn) ∈
−→
X (Ω) /x > c
o
RC =
n
(x1, x2, . . . , xn) ∈
−→
X (Ω) /x < c
o
Détermination du seuil critique c en utilisant le fait que :
α = P((X1, X2, . . . , Xn) ∈ RC|sous H0)
a’) σ2
connue
Dans ce cas, on sait que
X − m
σ
√
n
à N(0, 1)
P((X1, X2, . . . , Xn) ∈ RC| sousH0) = α
⇔ P
¡
X > c
¯
¯ m = m0
¢
= α
⇔ P
µ
X − m0
σ/
√
n
>
c − m0
σ/
√
n
¶
= α
⇔ P
µ
Z >
c − m0
σ/
√
n
¶
= α
⇔ P
µ
Z <
c − m0
σ/
√
n
¶
= 1 − α
⇒
c − m0
σ/
√
n
= Z1−α
P((X1, X2, . . . , Xn) ∈ RC| sousH0) = α
⇔ P
¡
X < c
¯
¯ m = m0
¢
= α
⇔ P
µ
X − m0
σ/
√
n
<
c − m0
σ/
√
n
¶
= α
⇔ P
µ
Z <
c − m0
σ/
√
n
¶
= α
⇒
c − m0
σ/
√
n
= Zα
⇒
c − m0
σ/
√
n
= −Z1−α
⇒ c = m0 + Z1−α ×
σ
√
n
⇒ c = m0 − Z1−α ×
σ
√
n
b’) σ2
inconnue
Dans ce cas, on sait que
X − m
S
√
n
à T (n − 1)
P((X1, X2, . . . , Xn) ∈ RC| sousH0) = α
⇐⇒ P
¡
X > c
¯
¯ m = m0
¢
= α
⇔ P
µ
X − m0
S/
√
n
>
c − m0
S/
√
n
¶
= α
⇔ P
µ
T >
c − m0
S/
√
n
¶
= α
⇔ P
µ
T <
c − m0
S/
√
n
¶
= 1 − α
⇒
c − m0
S/
√
n
= T
(n−1)
1−α
P((X1, X2, . . . , Xn) ∈ RC| sousH0) = α
⇔ P
¡
X < c
¯
¯ m = m0
¢
= α
⇔ P
µ
X − m0
S/
√
n
<
c − m0
S/
√
n
¶
= α
⇔ P
µ
T <
c − m0
S/
√
n
¶
= α
⇒
c − m0
S/
√
n
= T
(n−1)
α
⇒
c − m0
S/
√
n
= −T
(n−1)
1−α
⇒ c = m0 +
S
√
n
T
(n−1)
1−α ⇒ c = m0 −
S
√
n
T
(n−1)
1−α
Observation d’un échantillon et prise de décision
A partir de l’observation d’un échantillon de taille n, on calcule x et on décide :
de rejeter l’hypothèse H0 (donc m = m1) au risque α de se tromper si :
x > c x < c
d’accepter l’hypothèse H0 (donc m = m0) au risque α de se tromper si :
x ≤ c x ≥ c
Puissance du test :
P((X1, X2, . . . , Xn) ∈ RC| sousH1) = 1 − β
54

77. 3 Test sur la variance d’une loi normale
3.1 Test simple
On étudie sur la population mère un caractère X distribuée selon la loi normale
¡
m, σ2
¢
et on désire effectuer
au niveau de signification α un test sur le paramètre inconnu σ2
.
½
H0 : σ2
= σ2
0
H1 : σ2
= σ2
1
¡
σ2
1 6= σ2
0
¢
Selon le théorème de Neyman et Pearson, le test UPP de niveau de signification α est celui dont la région
critique est définie par : RC =
(
(x1, x2, . . . , xn)
,
L0
¡
x1, x2, . . . , xn, σ2
0
¢
L1 (x1, x2, . . . , xn, σ2
1)
< k
)
k > 0.
La vraisemblance de l’échantillon aléatoire de taille n est :
L (x1, x2, . . . , xn, σ) =
nQ
i=1
f(xi, σ) avec f(xi, σ) =
1
σ
√
2Π
e
−
1
2
xi − m
σ
2
est la ddp de la loi normale
⇒
⎧
⎪⎪⎪⎪⎪⎨
⎪⎪⎪⎪⎪⎩
L
¡
x1, x2, . . . , xn, σ2
0
¢
=
nQ
i=1
f(xi, σ2
0) =
nQ
i=1
1
σ0
√
2Π
e
−
1
2
xi − m
σ0
2
L
¡
x1, x2, . . . , xn, σ2
1
¢
=
nQ
i=1
f(xi, σ2
1) =
nQ
i=1
1
σ1
√
2Π
e
−
1
2
xi − m
σ1
2
⇒
L0
¡
x1, x2, . . . , xn, σ2
0
¢
L1 (x1, x2, . . . , xn, σ2
1)
=
nQ
i=1
1
σ0
√
2Π
exp
Ã
−
1
2
µ
xi − m
σ0
¶2
!
nQ
i=1
1
σ1
√
2Π
exp
Ã
−
1
2
µ
xi − m
σ1
¶2
!
=
µ
σ1
σ0
¶n nQ
i=1
"
exp
Ã
−
1
2
µ
xi − m
σ0
¶2
+
1
2
µ
xi − m
σ1
¶2
!#
=
µ
σ1
σ0
¶n
exp
Ã
nP
i=1
"
−
1
2
µ
xi − m
σ0
¶2
+
1
2
µ
xi − m
σ1
¶2
#!
=
µ
σ1
σ0
¶n
exp
∙µ
1
2σ2
1
−
1
2σ2
0
¶ nP
i=1
(xi − m)2
¸
L0
¡
x1, x2, . . . , xn, σ2
0
¢
L1 (x1, x2, . . . , xn, σ2
1)
< k ⇔ nLog
µ
σ1
σ0
¶
+
µ
1
2σ2
1
−
1
2σ2
0
¶ nP
i=1
(xi − m)
2
< Logk
⇔
µ
σ2
0 − σ2
1
σ2
1σ2
0
¶ nP
i=1
(xi − m)
2
< 2Logk − 2nLog
µ
σ1
σ0
¶
⇔
¡
σ2
0 − σ2
1
¢ nP
i=1
(xi − m)2
< σ2
1σ2
0
µ
2Logk − 2nLog
µ
σ1
σ0
¶¶
⇔
¡
σ2
0 − σ2
1
¢
ns02
0 < σ2
1σ2
0
µ
2Logk − 2nLog
µ
σ1
σ0
¶¶
⇔
¡
σ2
0 − σ2
1
¢
s02
0 <
σ2
1σ2
0
n
µ
2Logk − 2nLog
µ
σ1
σ0
¶¶
= k0
A ce niveau, deux cas peuvent se présenter : a) σ2
1 > σ2
0 ou b) σ2
1 < σ2
0
a) σ2
1 > σ2
0 b) σ2
1 < σ2
0
¡
σ2
0 − σ2
1
¢
< 0 ⇒ s02
0 >
k0
(σ2
0 − σ2
1)
= c
¡
σ2
0 − σ2
1
¢
> 0 ⇒ s02
0 <
k0
(σ2
0 − σ2
1)
= c
RC =
©
(x1, x2, . . . , xn)
±
s02
0 > c
ª
RC =
©
(x1, x2, . . . , xn)
±
s02
0 < c
ª
a’) m connue
Dans ce cas
1
σ2
Pn
i=1 (Xi − m)
2
=
nS02
0
σ2
à χ2
(n)
55

78. ⇒ P
¡
S02
0 > c
¯
¯ σ2
= σ2
0
¢
= α
⇔ P
µ
nS02
0
σ2
0
>
nc
σ2
0
¶
= α
⇔ P
µ
nS02
0
σ2
0
<
nc
σ2
0
¶
= 1 − α
⇒
nc
σ2
0
= χ2
1−α (n)
⇒ P
¡
S02
0 < c
¯
¯ σ2
= σ2
0
¢
= α
⇔ P
µ
nS02
0
σ2
0
<
nc
σ2
0
¶
= α
⇒
nc
σ2
0
= χ2
α (n)
⇒ c = χ2
1−α (n) ×
σ2
0
n
⇒ c = χ2
α (n) ×
σ2
0
n
⇒ RC (α) =
©
(x1, . . . , xn)
±
s02
0 > c
ª
=
½
(x1, . . . , xn)
Á
s02
0 > χ2
1−α (n) ×
σ2
0
n
¾ ⇒ RC (α) =
©
(x1, . . . , xn)
±
s02
0 < c
ª
=
½
(x1, . . . , xn)
Á
s02
0 < χ2
α (n) ×
σ2
0
n
¾
b’) m inconnue
1
σ2
Pn
i=1
¡
Xi − X
¢2
=
(n − 1) S2
σ2
à χ2
(n − 1)
⇒ P
¡
S2
> c
¯
¯ σ2
= σ2
0
¢
= α
⇔ P
µ
(n − 1) S2
σ2
0
>
(n − 1) c
σ2
0
¶
= α
⇔ P
µ
(n − 1) S2
σ2
0
<
(n − 1) c
σ2
0
¶
= 1 − α
⇒
(n − 1) c
σ2
0
= χ2
1−α (n − 1)
⇒ P
¡
S2
< c
¯
¯ σ2
= σ2
0
¢
= α
⇔ P
µ
(n − 1) S2
σ2
0
<
(n − 1) c
σ2
0
¶
= α
⇒
(n − 1) c
σ2
0
= χ2
α (n − 1)
⇒ c = χ2
1−α (n − 1) ×
σ2
0
(n − 1)
⇒ c = χ2
α (n − 1) ×
σ2
0
(n − 1)
⇒ RC (α) =
©
(x1, . . . , xn)
±
s2
> c
ª
=
½
(x1, . . . , xn)
Á
s2
> χ2
1−α (n − 1) ×
σ2
0
(n − 1)
¾ ⇒ RC (α) =
©
(x1, . . . , xn)
±
s2
< c
ª
=
½
(x1, . . . , xn)
Á
s2
< χ2
α (n − 1) ×
σ2
0
(n − 1)
¾
Observation d’un échantillon et prise de décision
4 Test sur une proportion
4.1 Test simple
On étudie sur la population mère un caractère X distribuée selon une loi de Bernoulli B (1, p) et on désire
effectuer au niveau de signification α un test sur le paramètre inconnu p. Soit (X1, X2, . . . , Xn) une EAS iid de
taille n (n ≥ 30) issu de cette population. ½
H0 : p = p0
H1 : p = p1
Selon le théorème de Neyman et Pearson, le test UPP de niveau de signification α est celui dont la région
critique est définie par : RC =
½
(x1, x2, . . . , xn)
Á
L0 (x1, x2, . . . , xn, p0)
L1 (x1, x2, . . . , xn, p1)
< k
¾
k > 0.
La vraisemblance de l’échantillon aléatoire de taille n est :
L (x1, x2, . . . , xn, p) =
nQ
i=1
f(xi, p) avec f(xi, p) = pxi
(1 − p)1−xi
⇒
⎧
⎪⎪⎨
⎪⎪⎩
L (x1, x2, . . . , xn, p0) =
nQ
i=1
f(xi, p0) =
nQ
i=1
pxi
0 (1 − p0)1−xi
L (x1, x2, . . . , xn, p1) =
nQ
i=1
f(xi, p1) =
nQ
i=1
pxi
1 (1 − p1)
1−xi
⇒
L0 (x1, x2, . . . , xn, θ0)
L1 (x1, x2, . . . , xn, θ1)
=
nQ
i=1
pxi
0 (1 − p0)
1−xi
nQ
i=1
pxi
1 (1 − p1)1−xi
=
nQ
i=1
µ
p0
p1
¶xi
∙
(1 − p0)
(1 − p1)
¸1−xi
56

79. ⇒
L0
¡
x1, x2, . . . , xn, σ2
0
¢
L1 (x1, x2, . . . , xn, σ2
1)
< k ⇔ Log
L0
L1
< Logk
⇔
nP
i=1
Log
µ
p0
p1
¶xi
∙
(1 − p0)
(1 − p1)
¸1−xi
< Logk
⇔
nP
i=1
∙
xiLog
µ
p0
p1
¶
+ (1 − xi) Log
(1 − p0)
(1 − p1)
¸
< Logk
⇔
nP
i=1
xi
| {z }
nf
∙
Log
µ
p0
p1
¶
− Log
(1 − p0)
(1 − p1)
¸
+ nLog
(1 − p0)
(1 − p1)
< Logk
⇔ nf × Log
µ
p0 (1 − p1)
p1 (1 − p0)
¶
< Logk − nLog
(1 − p0)
(1 − p1)
A ce niveau deux cas peuvent se présenter : a) p1 > p0 ⇒ Log
µ
p0 (1 − p1)
p1 (1 − p0)
¶
< 0 ⇒ f > c
b) p1 < p0 ⇒ Log
µ
p0 (1 − p1)
p1 (1 − p0)
¶
> 0 ⇒ f < c
N.B : n ≥ 30 ⇒ F Ã N
µ
p,
p (1 − p)
n
¶
⇒
F − p
r
p (1 − p)
n
à N(0, 1)
a) p1 > p0 b) p1 < p0
Forme de la région critique
RC =
n
(x1, x2, . . . , xn) ∈
−→
X (Ω) /f > c
o
RC =
n
(x1, x2, . . . , xn) ∈
−→
X (Ω) /f < c
o
Détermination du seuil critique c en utilisant le fait que :
α = P((X1, X2, . . . , Xn) ∈ RC|sous H0)
on a :
F − p
r
p (1 − p)
n
à N(0, 1)
P((X1, X2, . . . , Xn) ∈ RC| sousH0) = α P((X1, X2, . . . , Xn) ∈ RC| sousH0) = α
⇔ P (F > c| p = p0) = α
⇔ P
Ã
F − p0
p
p0 (1 − p0)/ n
>
c − p0
p
p0 (1 − p0)/ n
!
= α
⇔ P
Ã
Z >
c − p0
p
p0 (1 − p0)/ n
!
= α
⇔ P
Ã
Z <
c − p0
p
p0 (1 − p0)/ n
!
= 1 − α
⇒
c − p0
p
p0 (1 − p0)/ n
= Z1−α
⇔ P (F < c| p = p0) = α
⇔ P
Ã
F − p0
p
p0 (1 − p0)/ n
<
c − p0
p
p0 (1 − p0)/ n
!
= α
⇔ P
Ã
Z <
c − p0
p
p0 (1 − p0)/ n
!
= α
⇒
c − p0
p
p0 (1 − p0)/ n
= Zα
⇒
c − p0
p
p0 (1 − p0)/ n
= −Z1−α
⇒ c = p0 + Z1−α ×
r
p0 (1 − p0)
n
⇒ c = p0 − Z1−α ×
r
p0 (1 − p0)
n
57