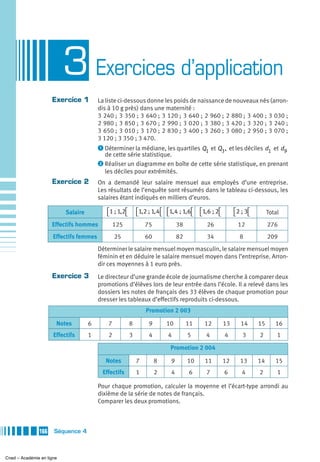
Le document traite des concepts de statistique et de probabilités, en abordant des sujets tels que la moyenne, la variance, l'écart-type, la médiane, et les quartiles. Il présente également des exercices d'application avec des exemples de calcul et des représentations graphiques comme les diagrammes en boîte. Enfin, il explique la transformation de données statistiques à l'aide de fonctions affines.